电脑桌面图标变白了?3个方法20秒钟轻松解
电脑桌面图标变白了?3个方法20秒钟轻松解
⚠️电脑桌面图标变白了,3种方法轻松解决
🚸方法一和方法二属于治标不治本的解决方法,但操作较为简单,在不同情况下有不成功的可能,方法三相对复杂一些,但是从根本处解决问题
·
·
·
✅ 方法一
·
1️⃣ 在白色图标处点右键,选择“属性”
·
2️⃣ 找到“快捷方式”,选择“更改图标”,再点击“确定”
·
3️⃣ 选择正确的图案,再点击“确定”,完成
·
·
·
✅ 方法二
·
1️⃣ 在白色图标处点右键,点击“打开文件所在的位置”
·
2️⃣ 在exe文件处点右键 点击“发送到”,选择“桌面快捷方式”,完成
·
·
·
✅ 方法三
·
1️⃣ win10系统 打开“此电脑”,点击 “查看”,勾选 “隐藏的项目”
(win11系统 打开“此电脑”,点击 “查看”,选择“显示”,勾选 “隐藏的项目”)
·
2️⃣ 同时 “Win + R”键打开运行,输入“%localappdata%” ,回车确定
右键“删除” lconCache.db文件
(用上诉方法显示 找不到文件 的同学,此电脑 > c盘 > 用户 > 你的电脑名称 > AppDate Local >IconCache.db 删除)
*删除之后不要关闭文件夹
·
3️⃣ 桌面最下方任务栏处 右键 打开任务管理器 (或者同时按“Shift + Ctrl + Del”键)
找到“Windows 资源管理器”,右键选择重新启动,完成
相关文章:

电脑桌面图标变白了?3个方法20秒钟轻松解
电脑桌面图标变白了?3个方法20秒钟轻松解 ⚠️电脑桌面图标变白了,3种方法轻松解决 🚸方法一和方法二属于治标不治本的解决方法,但操作较为简单,在不同情况下有不成功的可能,方法三相对复杂一些,…...

数据治理,管什么?
元数据(Metadata):通俗地说就是描述数据的数据,比如数据的名称、属性、分类、字段信息、大小、标签等等。要做好数据的管理,元数据起到了举足轻重的作用。 参考数据(Reference Data)࿱…...

【前端】JavaScript入门及实战121-125
文章目录 121 滚轮事件122 键盘事件123 键盘移动div124 BOM125 History 121 滚轮事件 <!DOCTYPE html> <html> <head> <title></title> <meta charset "utf-8"> <style type"text/css">#box1 {width: 100px;h…...

pytest测试框架之http协议接口测试
1 接口测试 日常测试中接口测试是一项重要的工作,尤其是http协议的接口测试更加普遍,比如一些常用的测试框架或者工具(robotframework框架,testng框架,postman等)都支持http接口的测试,而这节内容主要介绍…...

FFmpeg源码:av_gcd函数分析
一、引言 公约数,是一个能同时整除几个整数的数。如果一个整数同时是几个整数的约数,称这个整数为它们的“公约数”;公约数中最大的称为最大公约数。对任意的若干个正整数,1总是它们的公约数。 公约数与公倍数相反,就…...

springboot物流寄查系统-计算机毕业设计源码95192
目 录 1 绪论 1.1 研究背景 1.2选题背景 1.3论文结构与章节安排 2 springboot物流寄查系统系统分析 2.1 可行性分析 2.1.1 技术可行性分析 2.1.2 经济可行性分析 2.1.3 法律可行性分析 2.2 系统功能分析 2.2.1 功能性分析 2.2.2 非功能性分析 2.3 系统用例分析 2…...

【秋招笔试】24-07-27-OPPO-秋招笔试题(算法岗)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 💻 ACM金牌团队🏅️ | 多次AK大厂笔试 | 编程一对一辅导 ✨ 本系列打算持续跟新 秋招笔试题 👏 感谢大家的订阅➕ 和 喜欢💗 和 手里的小花花🌸 ✨ 笔试合集传送们 -> 🧷春秋招笔试合集 💡 第一题贪心模拟…...

AUTOSAR实战教程 - 模式管理BswM与其他各模块的交互
近日驻厂某OEM,幸得大块的个人时间, 把BswM这一块的内容从ETAS/ISOLAR工具配置到代码实现做了一个全方位的CT. 2024,希望孜孜内卷的汽车人升职加薪! 博主近期写的一首小诗,也一并送给大家,懂的都懂: 在看不到阳光的冬天/ 我染了风寒/ 白天点灯/ 晚上吃药/ 躺在被窝里才敢…...

经典非比较排序—计数排序的Java实现方式
目录 1.具体思路: 2.代码实现: 3.代码分析 4.示例测试: 测试源码: 测试结果: 计数排序,又被称为鸽巢原理,属于桶排序的一种,其本质是通过哈希映射思想,设定计数数组输入以…...

【C++从小白到大牛】栈和队列(优先级队列)
目录 引言: 使用方法篇: stack: queue priority_queue 使用方法: 模拟实现篇: stack: 原码: queue 原码: priority_queue 插入和删除数据的思想: 仿函数实…...
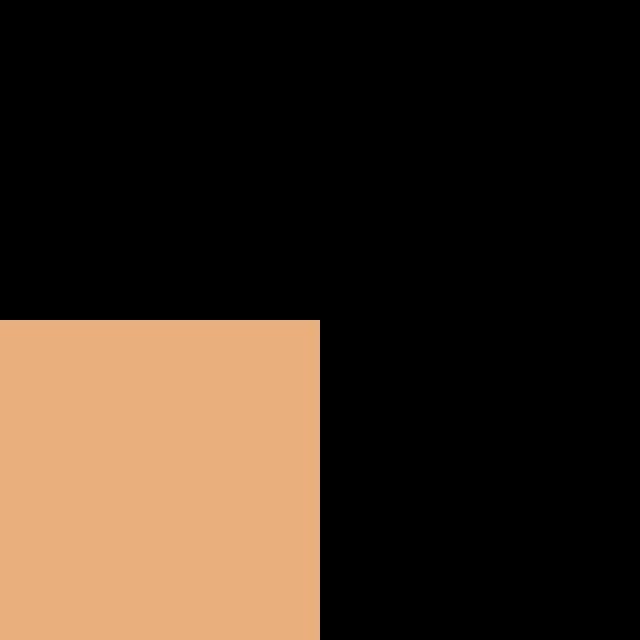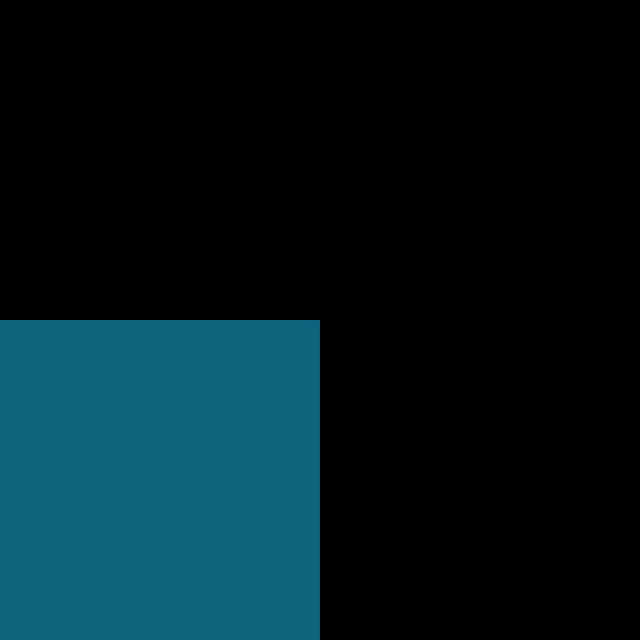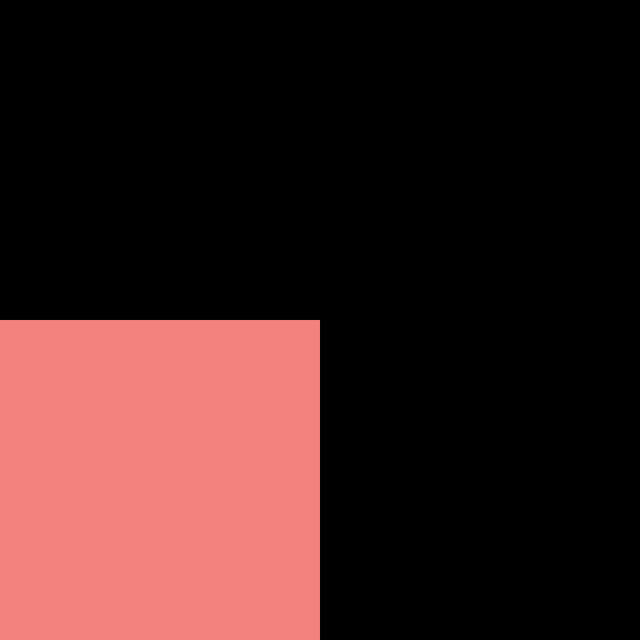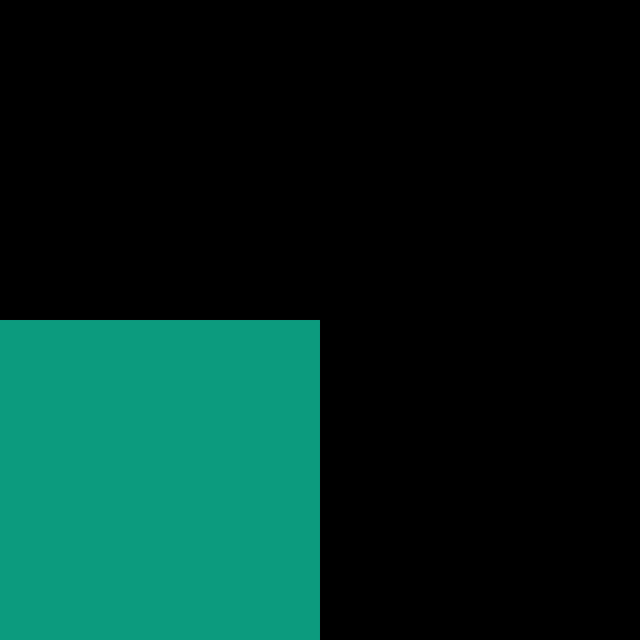
Golang之OpenGL(一)
使用OpenGL实现窗口中绘制三角形(纯色|彩色)、正方形(变色) 一、简单实现窗口绘制三角形二、绘制的多颜色三角形(基于 ‘ 简单实现窗口绘制三角形 ’ )1、在顶点着色器和片段着色器中添加了颜色的输入和输出…...

122. Go反射中与结构体相关的常用方法与应用
文章目录 encoding/jsonreflect 简介reflect.Value 常用方法reflect.Type 常用方法 应用一:使用 reflect 实现 encoding/json序列化反序列化 应用二:使用Tag实现字段级别的访问控制tag 行为自定义案例:结构体字段访问控制 总结 在使用 Go 语言…...

Java入门、进阶、强化、扩展、知识体系完善等知识点学习、性能优化、源码分析专栏分享
场景 作为一名Java开发者,势必经历过从入门到自学、从基础到进阶、从学习到强化的过程。 当经历过几年企业级开发的磨炼,再回头看之前的开发过程、成长阶段发现确实是走了好多的弯路。 作为一名终身学习的信奉者,秉承Java体系需持续学习、…...

Spring-bean销毁
bean销毁(找到销毁的bean) 在bean的声明周期中,存在一个记录bean销毁方法的阶段,以备于spring关闭的时候可以执行bean的销毁方法(单例bean) v1.0 registerDisposableBeanIfNecessary protected void registerDisposableBeanIfNec…...

【4】BlazorUI库
【4】BlazorUI库 一、Blazorise二、Ant Design Blazor三、Radzen Blazo四、Radzen Blazo 一、Blazorise Blazorise Blazorise 是一个广泛使用的 UI 框架,提供了丰富的组件库和多个主题支持,如 Bootstrap、Bulma、Material 和 AntDesign。 二、Ant Desig…...

树与二叉树【下】
目录 三. 哈夫曼树3.1 带权路径长度3.2 哈夫曼树的定义3.3 哈夫曼树的构造3.4 哈夫曼编码(经常考察) 四. 并查集4.1 如何表示“集合”关系?4.2 “并查集”的代码实现4.3 “并查集”的优化4.4 “并查集”的进一步优化 \quad 三. 哈夫曼树 \qua…...

ElementPlus 中el-select自定义指令实现触底加载请求options数据
1) 背景: 老项目翻新时,发现一个下拉框数据非常多,客户呢,希望全部数据一起展示,意思就是全部数据一起返回给前端用于展示。但这会造成明显的卡顿。~~明显的不合理! QAQ!~~ 于是压力给到前端,查询资料,各种…...

基于Selenium实现操作网页及操作windows桌面应用
Selenium操作Web页面 Why? 通常情况下,网络安全相关领域,更多是偏重于协议和通信。但是,如果协议通信过程被加密或者无法了解其协议构成,是无法直接通过协议进行处理。此时,可以考虑模拟UI操作,进而实现相…...

科普文:linux系列之操作系统内存管理简介
概叙 操作系统内存管理是计算机系统中的核心技术之一,页式管理、段式管理和段页式管理各有优缺点。页式管理通过固定大小的页框减少了外部碎片,但可能导致内部碎片;段式管理符合程序逻辑,提供了灵活的内存保护,但可能…...

【已解决】关于MyBatis的collection集合中只能取到一条数据的问题
一、问题 在涉及多表查询的时候,使用collection元素来映射集合属性时,出现了只能查询到一条数据的情况,但用sql语句在数据库中查询会有多条记录。 二、原因 如果两表联查,主表和明细表的主键都是id的话,明细表的多条…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
