数据结构初阶之排序(下)
前言
上一期内容中我们了解了基本排序中的插入与选择排序,今天我将为大家带来剩下的几种排序算法

快速排序
快速排序是Hoare于1962年提出的⼀种⼆叉树结构的交换排序⽅法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两⼦序列,左⼦序列中所有元素均⼩于基准值,右⼦序列中所有元素均⼤于基准值,然后最左右⼦序列重复该过程,直到所有元素都排列在相应位置上为⽌。
快速排序有着许多种实现方式,今天我们就hoare、挖坑法以及lomuto前后指针法来对其进行递归实现,同时还将运用数据结构中的栈来实现快速排序的非递归实现方法。
快速排序实现的主框架
//快速排序
void QuickSort(int* a, int left, int right)
{if (left >= right) {return;}//_QuickSort⽤于按照基准值将区间[left,right)中的元素进⾏划分 int meet = _QuickSort(a, left, right);QuickSort(a, left, meet - 1);QuickSort(a, meet + 1, right);
}
将区间中的元素进⾏划分的 _QuickSort ⽅法主要有以下⼏种实现⽅式:
我们可以将这些方法看做一个找基准值的过程:
hoare版本
思路:
1)创建左右指针,确定基准值
2)从右向左找出⽐基准值⼩的数据,从左向右找出⽐基准值⼤的数据,左右指针数据交换,进⼊下次循环
问题1:为什么跳出循环后right位置的值⼀定不⼤于key?
当 left > right 时,即right⾛到left的左侧,⽽left扫描过的数据均不⼤于key,因此right此时指向的数据⼀定不⼤于key
如图:

问题2:为什么left和right指定的数据和key值相等时也要交换?
相等的值参与交换确实有⼀些额外消耗。实际还有各种复杂的场景,假设数组中的数据⼤量重复时,⽆法进⾏有效的分割排序。
如图:

代码的实现
int _QuickSort(int* a, int left, int right)
{int begin = left;int end = right;int keyi = left;++left;while (left <= right){// 右边找⼩ while (left <= right && a[right] > a[keyi]){--right;}// 右边找⼩ while (left <= right && a[left] < a[keyi]){++left;}if (left <= right){swap(&a[left++], &a[right--]);}}swap(&a[keyi], &a[right]);return right;
}
挖坑法
思路:
创建左右指针。⾸先从右向左找出⽐基准⼩的数据,找到后⽴即放⼊左边坑中,当前位置变为新的"坑",然后从左向右找出⽐基准⼤的数据,找到后⽴即放⼊右边坑中,当前位置变为新的"坑",结束循环后将最开始存储的分界值放⼊当前的"坑"中,返回当前"坑"下标(即分界值下标)
我们通过一张图来了解:

代码的实现
int _QuickSort(int* a, int left, int right)
{int mid = a[left];int hole = left;int key = a[hole];while (left < right){while (left < right && a[right] >= key) {--right;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}
lomuto前后指针
思路:
创建前后指针,从左往右找⽐基准值⼩的进⾏交换,使得⼩的都排在基准值的左边。
如图:

代码的实现
int _QuickSort(int* a, int left, int right)
{int prev = left, cur = left + 1;int key = left;while (cur <= right){if (a[cur] < a[key] && ++prev != cur) {swap(&a[cur], &a[prev]);}++cur;}swap(&a[key], &a[prev]);return prev;
}
快速排序的特征
1. 时间复杂度:O(nlogn)
2. 空间复杂度:O(logn)
快速排序的非递归版本
⾮递归版本的快速排序需要借助数据结构:栈
根据栈结构先进后出的原则,我们先将待排序数组的末尾元素先入栈,头元素后入栈。
随后分别取栈顶与栈底元素,利用循环来实现递归操作。
代码的实现
void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);// 单趟 int keyi = begin;int prev = begin;int cur = begin + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;// [begin, keyi-1] keyi [keyi+1, end] if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}if (begin < keyi-1){STPush(&st, keyi-1);STPush(&st, begin);}}STDestroy(&st);
}
归并排序
归并排序的思想:
归并排序(MERGE-SORT)是建⽴在归并操作上的⼀种有效的排序算法,该算法是采⽤分治法(Divide and Conquer)的⼀个⾮常典型的应⽤。将已有序的⼦序列合并,得到完全有序的序列;即先使每个⼦序列有序,再使⼦序列段间有序。若将两个有序表合并成⼀个有序表,称为⼆路归并。归并排序核⼼步骤(如下图):

利用递归分别将待排序的数组二等分割成n份,每次取一半,随后就分割后的两两数组进行合并操作(先比大小后放置)
代码的实现
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right) {return;}int mid = (right + left) / 2;//[left,mid] [mid+1,right]_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = begin1;
//合并两个有序数组为⼀个数组 while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]) {tmp[index++] = a[begin1++];}else {tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}for (int i = left; i <= right; i++){a[i] = tmp[i];}
}
void MergeSort(int* a, int n)
{int* tmp = new int[n];_MergeSort(a, 0, n - 1, tmp);delete[] tmp;
}
归并排序的特征
1. 时间复杂度:O(nlogn)
2. 空间复杂度:O(n)
测试代码
通过以下代码,我们可以得出各种排序算法的时间效率。
// 测试排序的性能对⽐
void TestOP()
{ srand(time(0)); const int N = 100000;
int* a1 = (int*)malloc(sizeof(int)*N); int* a2 = (int*)malloc(sizeof(int)*N); int* a3 = (int*)malloc(sizeof(int)*N); int* a4 = (int*)malloc(sizeof(int)*N); int* a5 = (int*)malloc(sizeof(int)*N); int* a6 = (int*)malloc(sizeof(int)*N); int* a7 = (int*)malloc(sizeof(int)*N); for (int i = 0; i < N; ++i) { a1[i] = rand(); a2[i] = a1[i]; a3[i] = a1[i]; a4[i] = a1[i]; a5[i] = a1[i]; a6[i] = a1[i];a7[i] = a1[i]; } int begin1 = clock(); InsertSort(a1, N); int end1 = clock(); int begin2 = clock(); ShellSort(a2, N); int end2 = clock(); int begin3 = clock(); SelectSort(a3, N); int end3 = clock(); int begin4 = clock(); HeapSort(a4, N); int end4 = clock(); int begin5 = clock(); QuickSort(a5, 0, N-1); int end5 = clock(); int begin6 = clock(); MergeSort(a6, N); int end6 = clock(); int begin7 = clock(); BubbleSort(a7, N); int end7 = clock();printf("InsertSort:%d\n", end1 - begin1); printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3); printf("HeapSort:%d\n", end4 - begin4); printf("QuickSort:%d\n", end5 - begin5); printf("MergeSort:%d\n", end6 - begin6); printf("BubbleSort:%d\n", end7 - begin7); free(a1); free(a2); free(a3); free(a4); free(a5); free(a6); free(a7);
}
非比较排序
学习了以上的代码,那么有没有不通过比较大小就能实现的排序算法呢?有!
计数排序
计数排序⼜称为鸽巢原理,是对哈希直接定址法的变形应⽤。
操作步骤:
1)统计相同元素出现次数
2)根据统计的结果将序列回收到原来的序列中
通过两张图片来了解一下:


为了避免空间的无端浪费,我们将遍历待排数组中的最大最小值,后得出其间的差值,用其差值来申请空间大小以达到排序的效果。
代码的实现
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 1; i < n; i++){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail");return;}
memset(count, 0, sizeof(int) * range);// 统计次数 for (int i = 0; i < n; i++){count[a[i] - min]++;`}// 排序 int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}
计数排序的特征
计数排序在数据范围集中时,效率很⾼,但是适⽤范围及场景有限。
时间复杂度:O(N + range)
空间复杂度:O(range)
稳定性:稳定
*计数排序仅适用于整数的排序
排序算法的稳定性及其复杂度综合分析
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的 相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,⽽在排序后的序列中,r[i]仍在r[j]之 前,则称这种排序算法是稳定的;否则称为不稳定的。


以上便是数据结构初阶的全部内容,感谢各位的支持!后面我将为大家带来C++有关的知识分享,敬请期待!
相关文章:

数据结构初阶之排序(下)
前言 上一期内容中我们了解了基本排序中的插入与选择排序,今天我将为大家带来剩下的几种排序算法 快速排序 快速排序是Hoare于1962年提出的⼀种⼆叉树结构的交换排序⽅法,其基本思想为:任取待排序元素序列中的某元素作为基准值,…...

RGB图像的读取与保存
目录 1、安装imageio 2、读取照片 3、保存照片 4、resize 5、示例代码 1、安装imageio pip install imageio -i https://pypi.tuna.tsinghua.edu.cn/simple 2、读取照片 import imageio img imageio.imread(image_path) 3、保存照片 import imageio import numpy as…...

江协科技51单片机学习- p35 AD/DA模拟/数字采样
🚀write in front🚀 🔎大家好,我是黄桃罐头,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝…...

C#裁剪图像的几种方法总结
前言 我们在上位机软件开发过程中经常需要裁剪图像,本文就是对c#中常见的裁剪图像方法进行总结。 1、克隆 直接调用Bitmap的Clone函数,然后指定需要裁剪的区域即可裁剪图像,该种方法不会损失精度 public static Bitmap CropImage_Clone(Bi…...

被遗忘的哑终端 —— 键盘键位演变的启发者
注:机翻,未校对。 The Forgotten World of Dumb Terminals 被遗忘的哑终端世界 A quick journey through the lost age of “glass teletypes.” 快速穿越失落的“玻璃电传打字机”时代。 From the earliest days of digital computers, researchers o…...

APACHE安装与应用
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:Linux运维老纪的首页…...
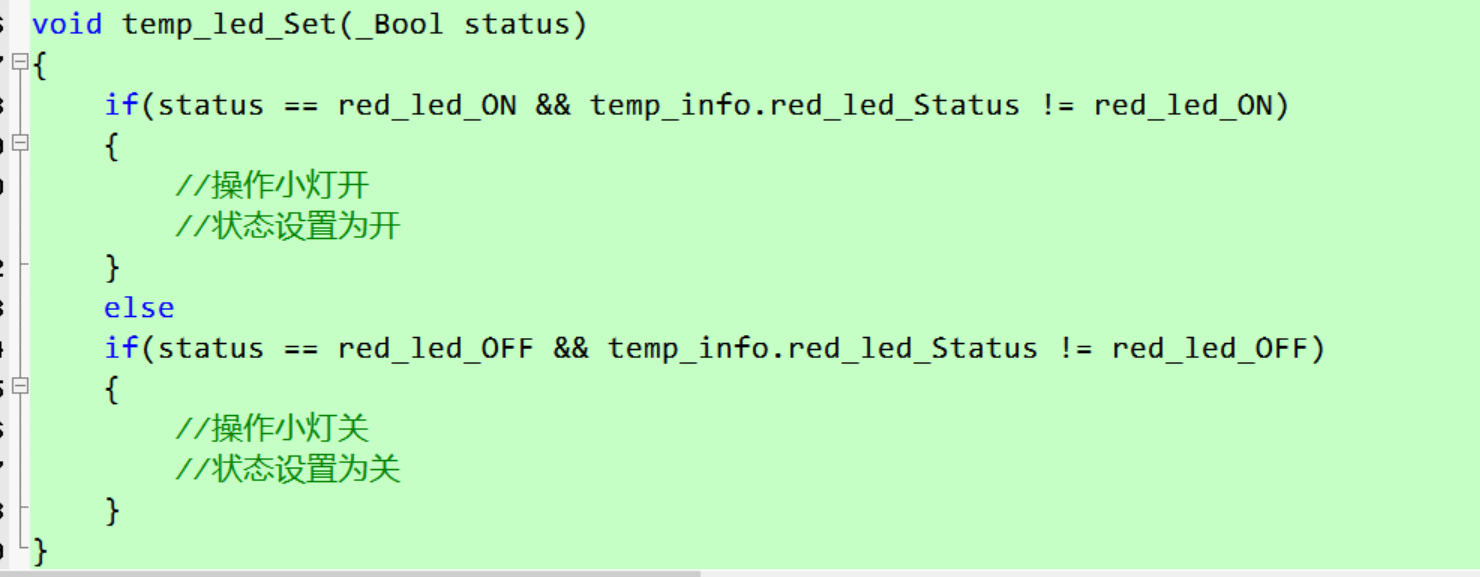
预警器件控制思考
预警器件控制思考 最小示例思想 当读取到环境信息与环境阈值的时候, 我们预警系统就要根据这些信息做出判断,是否要启动器件。 最简单的就是, 举温度temp的例子, temp(温度)与temp_th(阈值), 通过判断, 得出是否要启动器件. 如果在一段时间内, 一直是环境异常, 我…...

[Day 43] 區塊鏈與人工智能的聯動應用:理論、技術與實踐
區塊鏈的隱私保護機制 隨著區塊鏈技術的廣泛應用,隱私保護成為了一個至關重要的問題。區塊鏈以其去中心化和透明性的特點,為數據管理和交易提供了新的方法。然而,這些特點也帶來了新的挑戰,尤其是在隱私保護方面。本文將深入探討…...

【星海随笔】路由器的启动过程
路由器的启动过程 1.加电之后,ROM运行加电自检程序(Post),检查路由器的处理器、接口、内存等硬件设备。2.执行路由器中的启动程序(Bootstrap),搜索操作系统。路由器操作系统扩张部分可以从Flash RAM中装入,也可从 TFT…...
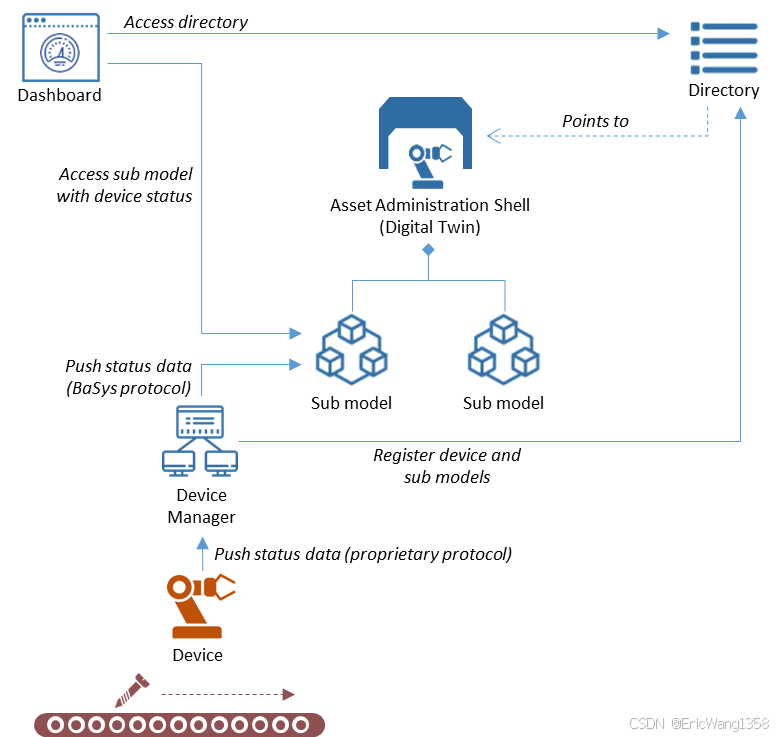
[翻译] Asset Administration Shells
关于资产管理外壳 (AAS) 资产管理外壳 (AAS) 是工业4.0中的关键概念,为产品、资源(如设备)和过程提供信息隐藏和更高层次的抽象。AAS 是技术和设备无关的机器可读描述,提供访问资产属性和功能的统一接口。与现有解决方案不同&…...

linux 常用磁盘维护命令
badblocks 功能说明:检查磁盘装置中损坏的区块。 语 法:badblocks [-svw][-b <区块大小>][-o <输出文件>][磁盘装置][磁盘区块数][启始区块] 补充说明:执行指令时须指定所要检查的磁盘装置,及此装置的磁盘区块数。…...
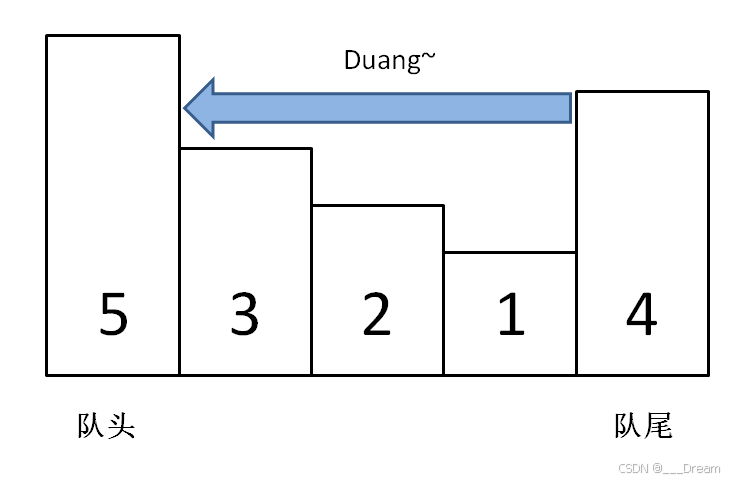
滑动窗口大总结!!!妈妈以后再也不担心我不会做滑动窗口啦~
写在前面:全部题都源于力扣 讲解题目一:最小覆盖子串题目二:字符串排列题目三:找所有字母异位词题目四:无重复字符的最长子串题目五:滑动窗口的最大值 讲解 滑动窗口算法技巧主要用来解决子数组问题&#…...

从地铁客流讲开来:客流统计与清分释义
一、常见的客流统计 1. 进站客流 定义:指在某个时间段内,乘客进入地铁站的数量。示例:如果某天早上8点到9点之间有5000人次进入地铁站,则这段时间内的进站客流为5000人次。 2. 出站客流 定义:指在某个时间段内&…...

《Excelize权威指南》新书发布
在数据洪流涌动的数字化时代,数据处理与分析已跃升为解锁无限洞察力的金钥匙,赋能商业智慧、重塑医疗健康版图、驱动教育科研创新。然而,当数据量级爆炸式增长,传统工具如 Excel 虽被誉为数据处理领域的常青树,其手动操…...
Go语言加Vue3零基础入门全栈班11 Go语言+gorm用户管理系统实战 2024年08月03日 课程笔记
概述 如果您没有Golang的基础,应该学习如下前置课程。 Golang零基础入门Golang面向对象编程Go Web 基础Go语言开发REST API接口_20240728Go语言操作MySQL开发用户管理系统API教程_20240729Redis零基础快速入门_20231227GoRedis开发用户管理系统API实战_20240730Mo…...
【设计模式】代理模式详解
1.简介 代理模式是常用的Java设计模式,该模式的特点是代理类与委托类共享相同的接口。代理类主要负责预处理消息、过滤消息、将消息转发给委托类,并在事后处理消息等。代理类与委托类之间通常存在关联关系,一个代理类对象与一个委托类对象关…...

Python变量和简单的数据类型
1、变量 massageHello python world! print(massage) massageHello world print(massage) 运行这个代码发现,同一个变量出现两个不同的结果 Hello python world! Hello world 在程序中,可随时修改变量的值&…...

切比雪夫距离
切比雪夫距离(Chebyshev Distance),又称棋盘距离或最大值距离,是一种用于测量两个点之间距离的度量方法。在二维平面上,切比雪夫距离定义为两个点之间的最大坐标差值。其公式如下: DChebyshevmax(∣x2−…...
教程 —— 第4章 计算机网络与Internet(下))
计算机基础(Windows 10+Office 2016)教程 —— 第4章 计算机网络与Internet(下)
第4章 计算机网络与Internet 4.4 局域网4.4.1 局域网概述4.4.2 以太网4.4.3 令牌环网4.4.4 无线局域网 4.5 Internet4.5.1 Internet 概述4.5.2 Internet 的基本概念4.5.3 Internet 的接入4.5.4 万维网 4.6 Internet的应用4.6.1 电子邮件4.6.2 文件传输4.6.3 搜索引擎 4.4 局域网…...

机器学习用Python还是R?哪个更好一些?
选择使用Python还是R来进行机器学习取决于多个因素,包括个人偏好、项目需求以及可用的资源。这里我可以简要比较一下它们的优缺点: Python的优势: 通用性和灵活性: Python是一种通用编程语言,可以用于多种用途&#…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

【动态规划】B4336 [中山市赛 2023] 永别|普及+
B4336 [中山市赛 2023] 永别 题目描述 你做了一个梦,梦里有一个字符串,这个字符串无论正着读还是倒着读都是一样的,例如: a b c b a \tt abcba abcba 就符合这个条件。 但是你醒来时不记得梦中的字符串是什么,只记得…...
