java算法day28
java算法day28
- 300 最长递增子序列
- 136 只出现一次的数字
- 169 多数元素
- 234 回文链表
- 53 最大子数组和
300 最长递增子序列
这个是记忆化搜索的代码。是从递归改过来的。
这题显然是要用dp做比较合适。因为很容易看到原问题与子问题之间的关系。
还是从后往前看。
然后可以利用选与不选,或者选哪个。这两种方式来进行拆分,然后进行递归。
class Solution {int[] memo;public int lengthOfLIS(int[] nums) {if(nums==null||nums.length==0){return 0;}int n = nums.length;memo = new int[n];int maxLen = 0;for(int i = n-1;i>=0;i--){maxLen = Math.max(maxLen,dfs(nums,i));}return maxLen;}int dfs(int[] nums,int index){if(index == 0){return 1;}if(memo[index]!=0){return memo[index];}int maxLen = 1;for(int i = index-1;i>=0;i--){if(nums[i]<nums[index]){maxLen = Math.max(maxLen,dfs(nums,i)+1);}}memo[index] = maxLen;return maxLen;}}
如果你熟悉了递归转记忆化搜索转动态规划这个模式。那么可以直接来看动态规划怎么写了。
如果你懂这个过程,那么完全可以看懂递归模板这样做的原因。以及找到这些相关因素到底能有什么用。详细的总结我写在最后面那个题了。我们来看这题dp怎么做
状态定义:
dp[i]的值代表nums以nums[i]结尾的最长子序列的长度。
状态转移方程。
136 只出现一次的数字
思路:
拿到题目首先看到题目的含义,就想到了统计数字出现次数,那么就想到了Hash。但是题目不让用额外的空间,那么哈希没用了。
那么往不用空间复杂度想,我又想到了排序,但是排序最快也要o(nlogn),题目又要用o(n)时间复杂度,于是排序也没有了。
然后去看题解了。
这个解法完全是因为题目的含义才能解出来:
除了某个元素只出现一次之外,其余元素均出现2次。
这非常符合位运算的性质。你要是知道这个性质,你也可以做:
既满足时间复杂度又满足空间复杂度,就要提到位运算中的异或运算 XOR,主要因为异或运算有以下几个特点:
一个数和 0 做 XOR 运算等于本身:a⊕0 = a
一个数和其本身做 XOR 运算等于 0:a⊕a = 0
XOR 运算满足交换律和结合律:a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b
由于满足交换律和结合律,那么按顺序遍历一遍进行异或运算,那么最后出现两次的肯定异或得到0了。
最后的情况肯定是这个单独的出现的元素异或0得到他本身,返回这个结果就结束了。
class Solution {public int singleNumber(int[] nums) {if(nums.length == 1){return nums[0];}int length = nums.length;//取第一个元素就开始遍历,然后返回最后的结果。int ans = nums[0];for(int i = 1;i<length;i++){ans^=nums[i];}return ans;}
}
169 多数元素
那道题想到两个想法:
1、哈希,2、排序。
class Solution {public int majorityElement(int[] nums) {Map<Integer,Integer> map = new HashMap<>();int length = nums.length;for(int i = 0;i<length;i++){if(map.containsKey(nums[i])){int value = map.get(nums[i]);map.put(nums[i],value+1);}else{map.put(nums[i],1);}}int target = length/2;for(Map.Entry<Integer,Integer> entry : map.entrySet()){int value = entry.getValue();if(value > target){return entry.getKey();}}return 0;}
}
最优解
摩尔投票
思路:
候选人candNum初始化为nums[0],票数count初始化为1。
当遇到与candNum相同的数,则票数count=count+1。
否则票数-1。
一旦count为0时,更换候选人。
遍历完数组之后,candNum即为最终答案。
原理解释:
该方法属于投票法
投票法是遇到相同的则票数+1,不同的票数-1。且众数元素的个数大于总元数的一半,其余元素的个数肯定小于一般。
因此多数元素的个数-其余元素的个数总和的结果肯定>=1。这就相当于按照这种抵消策略。最后肯定会剩余至少1个多数元素。
之前我脑子里一直有那种类似这样的例子:
1 2 1 3 1 4 1 5 。这个纯粹就是我少想了,一定是大于半数。注意是大于。所以这个思路完全行得通。
class Solution {public int majorityElement(int[] nums) {if(nums.length==1){return nums[0];}int length = nums.length;int candNum = nums[0];int count = 1;for(int i = 1;i<length;i++){if(count==0){candNum = nums[i];}if(nums[i]==candNum){count++;}else{count--;}}return candNum;}
}
234 回文链表
主要思路:
先找到中间节点:通过快慢指针,fast一次两步,slow一次一步。然后将后半段链表逆置。然后进行回文的逻辑判断即可。
关键点。其实不用考虑中间若是多一个节点的情况,多出来的那个节点完全不会比较到,因为没有比这个元素的机会,当少1个元素的链表遍历完的时候,我循环比较的逻辑就停止了。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public boolean isPalindrome(ListNode head) {if(head.next==null){return true;}ListNode fast = head;ListNode slow = head;while(fast!=null && fast.next!=null ){slow = slow.next;fast = fast.next.next;}//此时slow已经在中。然后将后面的链表逆置了ListNode pre = null;ListNode cur = slow;while(cur!=null){//存后一个节点ListNode next = cur.next;cur.next = pre;pre = cur;cur = next;}//现在来进行回文的判断ListNode l1 = head;ListNode l2 = pre;while(l1!=null && l2!=null){if(l1.val!=l2.val){return false;}l1 = l1.next;l2 = l2.next;}return true;}
}
53 最大子数组和
有了前面的积累,我终于能直接看懂动态规划的题解了。也终于知道状态转移方程怎么用了。
这里可以总结一下心路历程:
看懂动态规划之前有这样的历程:首先动态规划不是上来就有的。首先应该是暴力递归解法。将递归树画出来后,我们可以发现可以优化的点,那就是递归的过程存在很多的重复计算,那这个时候就需要“备忘录”来存储重复的计算。那么这个时候我们对这颗树做优化,你会发现这个递归树突然就变成了o(n)的量级。从递归树来看,那直接就是一路归并,值指最优值。
而这个归并正是状态转移方程。所以为什么很多题解给个初始状态,给个状态转移方程就说这个题就做完了。所以说,有时感觉这个题有很多种走法,但偏偏为什么动态规划是最优走法,就是这个原因。
本题动态规划思路:
dp[i]表示以nums[i]结尾的最大子数组和。然后一般我们从后往前思考。
分类讨论:
我把这种推导过程称之为拼与不拼。不拼那么就重起一个子数组了。
情况1:nums[i] 单独组成一个子数组,那么dp[i] = nums[i]。这种情况是纯在的,比如-1,-2,-5,7,-2,-3。那么以7这个位置为结尾的最长子数组和应该只有7本身。
情况2:将nums[i]和前面的子数组拼起来,也就是以nums[i-1]结尾的最大子数组和之和添加nums[i]。那么此时dp[i] = f[i-1]+nums[i]。
那么这个原问题和子问题的关系就很明确了。
由于每个元素都有可能是最长子数组和的结尾元素。那么可写出这个递推公式
f[i] = max(f[i-1],0) + nums[i]。
自己理解一下这个公式,这个状态转移方程的意思就是上面的两种情况。
如果f[i-1]比0还小,那说明把前面的子数组加起来是没有收益的,那么就要重起一个子数组了,此时前面这个式子值为0。此时f[i] = nums[i]。
如果你是非常清楚dp的套路。那么我告诉你一个结论,然后一个公式你应该就做完了。
1、dp[i]表示以nums[i]结尾的最长子数组的和。
2、状态转移方程:
初始状态那么就是dp[0],那么就是以nums[0]结尾的最长子数组,那么dp[0]= nums[0]。
3、循环迭代计算dp数组,然后找出以哪个为值为结尾的子数组和最大。然后返回这个最大值。
class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];dp[0] = nums[0];int ans = dp[0];for(int i = 1;i<nums.length;i++){dp[i] = Math.max(dp[i-1],0) + nums[i];ans = Math.max(ans,dp[i]);}return ans;}
}
相关文章:

java算法day28
java算法day28 300 最长递增子序列136 只出现一次的数字169 多数元素234 回文链表53 最大子数组和 300 最长递增子序列 这个是记忆化搜索的代码。是从递归改过来的。 这题显然是要用dp做比较合适。因为很容易看到原问题与子问题之间的关系。 还是从后往前看。 然后可以利用选…...

vue实现歌词滚动效果
1.结构 <template><div class"lyricScroll"><div class"audio"><audio id"audio" src"./common/周传雄-青花1.mp3" controls></audio></div><div class"container" id"contai…...

【算法设计题】合并两个非递减有序链表,第1题(C/C++)
目录 第1题 合并两个非递减有序链表 得分点(必背) 题解 函数声明与初始化变量: 初始化合并链表的头节点: 合并两个链表: 处理剩余节点: 返回合并后的链表: 完整测试代码 🌈…...

Vue前端工程
创建一个工程化的vue项目 npm init vuelatest 全默认回车就好了 登录注册校验 //定义数据模型 const registerDataref({username:,password:,rePassword: }) //校验密码的函数 const checkRePassword(rule,value,callback)>{if (value){callback(new Error(请再次输入密…...

什么是药物临床试验?
药物临床试验是指在人体上进行的新药试验研究,旨在确定新药的疗效、安全性、药代动力学和药效学。临床试验不仅帮助确认药物是否对特定疾病或症状有效,还帮助识别和评估药物的副作用和风险。 药物临床试验(Clinical Trial,CT&…...

编译和汇编的区别
一、编译 编译是将高级语言(如C、C、Java等)编写的源代码转换成计算机可以直接执行的低级语言(通常是机器语言或汇编语言)的过程 编译 —— 将人类可读的源代码转换为计算机可执行的指令集 编译过程 通常包括词法分析、语法分…...

C# 设计倒计时器、串口助手开发
文章目录 1. 实现一个简单的倒计时器开始、暂停2. 串口助手开发 1. 实现一个简单的倒计时器开始、暂停 namespace Timer {public partial class Form1 : Form{int count;//用于定时器计数int time;//存储设定的定时值bool parse false;//控制暂停计时public Form1(){Initiali…...

图论① dfs | Java | LeetCode 797,Kama 98 邻接表实现(未完成)
797 所有可能路径 https://leetcode.cn/problems/all-paths-from-source-to-target/description/ 输入:graph [[1,2],[3],[3],[]] 题目分析,这里 class Solution {//这个不是二维数组,而是listList<List<Integer>> res new Ar…...

Mac安装nvm以及配置环境变量
安装nvm brew install nvm安装成功后会出现这样一段话: Add the following to your shell profile e.g. ~/.profile or ~/.zshrc:export NVM_DIR"$HOME/.nvm"[ -s "/opt/homebrew/opt/nvm/nvm.sh" ] && \. "/opt/homebrew/opt/nvm/nvm.sh&q…...

AUTOSAR实战教程-使用DET来发现开发错误
2年之前因为在调试AUTOSAR存储协议栈的时候使用DET并没发现有用的信息,所以就武断下结论--这玩意没有用。活到老学到老吧,bug经历的多了,发现这玩意还挺有用的。说一下这个bug的背景。 在将时间同步报文改道CanTsync之后,由于这个AUTOSAR工具本身的问题以及配置工程师本身的…...
:请求-响应模式,C和C++。)
ZeroMQ(二):请求-响应模式,C和C++。
目录 请求响应基础 基本概念 工作流程 典型应用 请求-响应模式的特点 应用实例 优点 缺点 ZEROMQ C语言 2.1 服务器端代码(Reply Server) 2.2 客户端代码(Request Client) 3. 编译代码 4. 详细说明 ZEROMQ C 1. …...

【虚拟仿真】Unity3D中实现2DUI显示在3D物体旁边
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址QQ群:398291828大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 这篇文章来实现2DUI显示在3D物体旁边,当我们需要在3D模型旁边显示2DUI的时候,比如人物的对…...

代码随想录 day 29 贪心
第八章 贪心算法 part03 134. 加油站 本题有点难度,不太好想,推荐大家熟悉一下方法二 https://programmercarl.com/0134.%E5%8A%A0%E6%B2%B9%E7%AB%99.html 135. 分发糖果 本题涉及到一个思想,就是想处理好一边再处理另一边,不…...
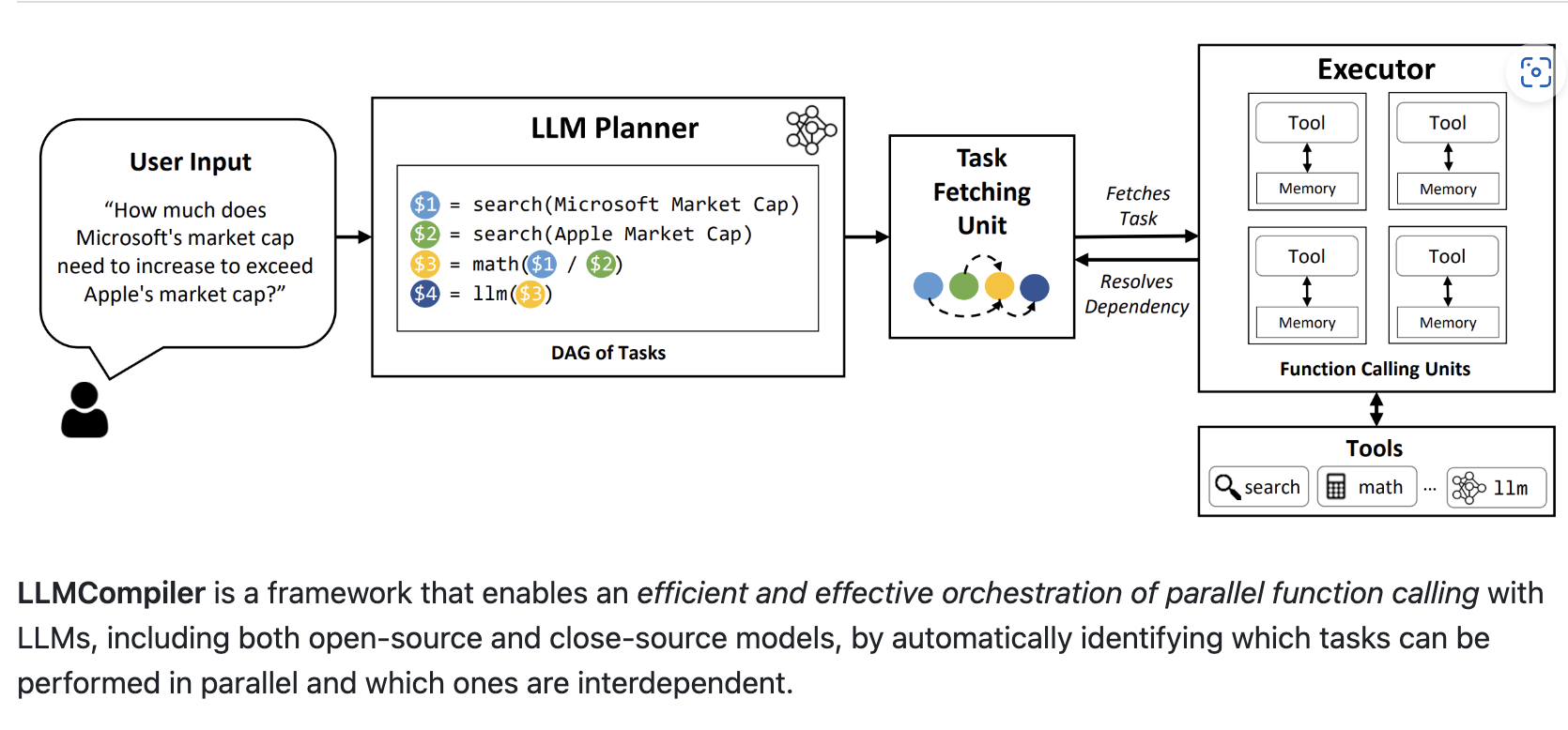
开源:LLMCompiler高性能工具调用框架
开源:LLMCompiler高性能工具调用框架 LLMCompilerLLMCompiler 框架图任务提取单元使用方式参考链接 LLMCompiler LLMCompiler 是一种 Agent 架构,旨在通过在DAG中快速执行任务来加快 Agent 任务的执行速度。它还通过减少对 LLM 的调用次数来节省 Tokens …...

【学习方法】高效学习因素 ① ( 开始学习 | 高效学习因素五大因素 | 高效学习公式 - 学习效果 = 时间 x 注意力 x 精力 x 目标 x 策略 )
文章目录 一、高效学习因素1、开始学习2、高效学习因素五大因素3、高效学习公式 - 学习效果 时间 x 注意力 x 精力 x 目标 x 策略 一、高效学习因素 1、开始学习 对于 学习差 , 调皮捣蛋 的学生 , 不要把 学习成绩差 的 原因 归因为 不爱学习 / 没有学习方法 , 可能是 还没有 …...

LeetCode Medium|【146. LRU 缓存】
力扣题目链接 题意:本题的题意就是希望我们设计一个满足 LRU 缓存的数据结构,LRU即最近最少使用。 需要我们实现 get 和 put 方法,即从缓存中获取值和设置缓存中值的方法。 还有一个约束条件就是缓存应当有容量限制,如果实现 put …...

(南京观海微电子)——LCD OTP(烧录)介绍
OTP OTP只是一种存储数据的器件,全写:ONETIMEPROGRAM。 OTP目的:提高产品的一致性 客户端的接口不支持和我们自己的产品IC之间通信,即不支持写初始化,所以产品的电学功能以及光学特性需要固化在IC中,所以需要我们来进行…...

[E二叉树] lc572. 另一棵树的子树(dfs+前中序判断+树哈希+树上KMP+好题)
文章目录 1. 题目来源2. 题目解析 1. 题目来源 链接:572. 另一棵树的子树 2. 题目解析 看到这个题目就感觉不简单,因为写了写 dfs 版本的,发现好像不太会… 还是简单粗暴一点,直接搞一个 前序中序,进行判断即可。我…...

C# 设计模式之简单工厂模式
总目录 前言 本文是个人基于C#学习设计模式总结的学习笔记,希望对你有用! 1 基本介绍 简单工厂模式 定义:用于创建对象,将对象的创建与使用分离。 简单工厂模式中用于创建实例的方法是静态(static)方法,因而简单工厂…...

mac中dyld[5999]: Library not loaded: libssl.3.dylib解决方法
需要重新安装下openssl3.0版本 brew reinstall openssl3.0 安装后执行还是报错,需要找到openssl的安装路径 /opt/homebrew/Cellar/openssl3.0/3.0.14/lib/ 将libssl.3.dylib和libcrypto.3.dylib拷贝到自己的二进制文件同目录下,再执行二进制文件就可…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
