【算法】双指针-OJ题详解1
双指针-OJ题
- 移动零(点击跳转)
- 原理讲解
- 代码实现
- 复写零(点击跳转)
- 原理讲解
- 代码实现
- 快乐数(点击跳转)
- 原理讲解
- 代码实现
- 盛最多水的容器(点击跳转)
- 原理讲解
- 代码实现
- 有效三角形的个数(点击跳转)
- 原理讲解
- 代码实现
- 查找总价值为目标值的两个商品(点击跳转)
- 原理讲解
- 代码实现
- 三数之和(点击跳转)
- 原理讲解
- 代码实现
- 四数之和(点击跳转)
- 原理讲解
- 代码实现
移动零(点击跳转)

原理讲解


因此我们定义两个指针:
- cur:遍历数组
- dest:已处理的区间内,最后一个非零元素的位置
这样就把数组划分成三块区间:
[0 , dest] 、[dest+1 , cur-1] 、[cur , size-1]
分别对应:
非零元素、零、待处理
具体操作:
cur遍历过程中
- 遇到0元素
cur++; - 遇到非0元素
swap(dest+1,cur); //swap数组中下标为dest+1和cur的元素
dest++;cur++;
代码实现
void moveZeroes(vector<int>& nums) {int dest = -1;int cur = 0;while (cur < nums.size()){if (nums[cur])swap(nums[++dest], nums[cur]);cur++;}
}
复写零(点击跳转)

原理讲解
这道题首先要想到从后向前遍历,因为如果从前向后遍历,会覆盖掉后面的值,较难操作,因此:


第一步找到最后一个数,可以用快慢指针来实现:cur指针、dest指针。前者从前向后遍历,后者根据前者位置的值走1步或2步,具体如下:
- 先判断cur位置的值
- 若cur位置的值非0,dest向后移动一步;若cur位置的值为0,dest向后移动2步
- 判断dest位置是否到了结束的位置
- cur++
代码实现
void duplicateZeros(vector<int>& arr) {int dest = -1;int cur = 0;//找到最后一个数while (cur < arr.size()){if (arr[cur])dest++;elsedest += 2;if (dest >= arr.size() - 1)break;cur++;}
//处理特殊情况:cur指向的最后一个数是0,dest越界if (dest == arr.size()){arr[dest - 1] = 0;cur--;dest -= 2;}
//复写while (cur >= 0){if (arr[cur])arr[dest--] = arr[cur--];else{arr[dest--] = 0;arr[dest--] = 0;cur--;}}
}
快乐数(点击跳转)

原理讲解

最后一定会成环(可以证明,用鸽巢原理)
因此可以通过判断环的起点是否为1,决定返回true还是false
→ 快慢指针
快慢指针有⼀个特性,就是在⼀个圆圈中,快指针总是会追上慢指针的,也就是说他们总会相遇在⼀个位置上。就本题而言,如果相遇位置的值是 1 ,那么这个数⼀定是快乐数;如果相遇位置不是 1 ,那么就不是快乐数。
代码实现
//求x每一位数的平方和int SqSum(int x){int ret = 0;while(x){int n = x%10;ret += n*n;x/=10;}return ret;}bool isHappy(int n) {int slow = n,fast = SqSum(n);//fast不能设成n,否则进不了循环while(slow != fast){slow = SqSum(slow);fast = SqSum(SqSum(fast));}return slow==1;}
盛最多水的容器(点击跳转)

原理讲解
我们首先想到的大概率是两层循环暴力枚举,但是复杂度高,这道题不能通关
那应该如何解这题呢?
首先,容器的容积(这道题只考虑面积)是S = h * w
h表示高度,即height[?]
w表示宽度,即两条垂线间隔的距离
为了方便叙述,我们假设左边边界height[left]小于右边边界height[right]。
如果此时我们固定⼀个边界,改变另⼀个边界,水的容积会有如下变化形式:
- 容器的宽度w一定变小。
- 由于左边界较小,决定了水的高度。①如果改变左边界,新的水面高度不确定,但是一定不会超过右边的柱子高度,因此容器的容积可能会改变(可能变大、变小、不变)。
- ②如果改变右边界,无论右边界移动到哪里,新的水面的高度一定不会超过左边界,也就是不会超过现在的水面高度,但由于容器的宽度减小,因此容器的容积⼀定会变小的。
所以我们可以舍去情况②,只需要讨论情况①(因为我们的目的是求最大的容积)
因此,我们定义两个指针left和right,然后比较height[left] 和 height[right],移动height小的位置的指针,循环这个过程,期间产生的所有的容积里的最大值,就是要return的最终答案
代码实现
int maxArea(vector<int>& height) {int left = 0;int right = height.size()-1;int _max = 0;while(left < right){int tmp = (right-left)*min(height[right],height[left]);_max = max(_max,tmp);if(height[left] < height[right])left++;elseright--; }return _max;}
有效三角形的个数(点击跳转)

原理讲解
我们小学五年级都学过,三角形的三条边必须满足:任意两边之和大于第三边、任意两边之差小于第三边~
假设三角形三条边长度分别为:a, b, c
-
方法① a+b < c ; a+c < b ; b+c < a
-
方法② 在①的基础上优化:先排序,a ≤ b ≤ c,只需要判断 a+b > c即可
解法一:三层循环暴力枚举 → O(n3)
解法二:利用(排序后)单调性,用双指针算法来解决。 → O(n2)
- 先固定最大的数
- 在最大数的左边区间内,用双指针算法,快速统计出符合要求的另外两个数:
-
- 如果
nums[left]+nums[right]>nums[max],说明 [left, right - 1] 区间上的所有元素均可以与nums[right]构成比nums[max]大的二元组,此时满足条件的有 right - left 种;此时 right 位置的元素的所有情况相当于全部考虑完毕, right-- ,进入下一轮判断
- 如果
-
- 如果
nums[left]+nums[right]<=nums[max],说明 left 位置的元素是不可能与 [left + 1, right] 位置上的任意元素构成满足条件的二元组,left++进入下一轮循环
- 如果
- 向左移动最大数,循环上面的过程
代码实现
int triangleNumber(vector<int>& nums) {int left,right;int cmax = nums.size() - 1;int ret = 0;sort(nums.begin(),nums.end());while (cmax > 1) {left = 0;right = cmax-1;while (left < right) {if (nums[left] + nums[right] > nums[cmax]) {ret+=(right-left);right--; } else {left++;}}cmax--;//向左移动最大数}return ret;}
查找总价值为目标值的两个商品(点击跳转)

原理讲解
类比上面《有效三角形的个数》,会发现利用单调性同样很香:利用对撞指针优化时间复杂度
- 初始化
left,right分别指向数组的左右两端 - 接下来无非三种情况:
-
price[left]+price[right]==target,说明找到了,跳出循环返回即可
-
price[left]+price[right]>target,说明两数之和大了,right–
-
price[left]+price[right]<target,说明两数之和小了,left++
代码实现
vector<int> twoSum(vector<int>& price, int target) {int left = 0,right = price.size()-1;vector<int> ret;while(left < right){if(price[left] + price[right] == target){ret.push_back(price[left]);ret.push_back(price[right]);break;}else if(price[left] + price[right] > target)right--;elseleft++;}return ret;}
或者不需创建vector直接返回:
vector<int> twoSum(vector<int>& price, int target) {int left = 0,right = price.size()-1;while(left < right){if(price[left] + price[right] == target)return {price[left] , price[right]};else if(price[left] + price[right] > target)right--;elseleft++;}return {-1};//注意这里必须return一个数组,目的是照顾编译器,否则编译不通过}
三数之和(点击跳转)

原理讲解
我们可以利用在两数之和那道题的双指针思想,来对暴力枚举做优化:
- 先排序
- 然后固定一个数 a
- 在这个数后面的区间内,利用双指针快速找到两个数之和等于 -a 即可
但是要注意的是,这道题需要有去重操作~
(除了用set,我们可以自己实现)
- 找到一个结果之后, left 和 right 指针要跳过重复的元素;
- 当用完⼀次双指针算法之后,固定的 a 也要跳过重复的元素。
代码实现
vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(),nums.end());int i =0,left,right;vector<vector<int>> vv;while(i < nums.size()-2){if(nums[i] > 0)break;//left+rightleft = i+1;right = nums.size()-1;while(left < right && right < nums.size()){if(nums[left] + nums[right] == -nums[i]){vv.push_back({nums[i],nums[left],nums[right]});left++;right--;while(left < right && right < nums.size()&&nums[left] == nums[left-1])left++;//left跳过重复元素while(left < right && right < nums.size()&&nums[right] == nums[right+1])right--;//right跳过重复元素}else if(nums[left] + nums[right] > -nums[i])right--;elseleft++;}i++;while(nums[i] == nums[i-1] && i<nums.size()-2)++i;//“固定”的数跳过重复元素}return vv; }
四数之和(点击跳转)

原理讲解
这道题和上面的《三数之和》几乎一模一样,区别在于多了一层
- 固定一个数a
- 在这个数 a 的后面区间上,利用「三数之和」找到三个数,使这三个数的和等于
target - a即可
代码实现
vector<vector<int>> fourSum(vector<int>& nums, int target) {sort(nums.begin(),nums.end());vector<vector<int>> vv;int i=0,j,left,right;while(i<nums.size()){j = i+1;while(j<nums.size()){left = j+1;right = nums.size()-1;long long aim = (long long)target-nums[i]-nums[j];//有些用例不强转会越界while(left<right){int sum =nums[left]+nums[right];if(sum == aim){vv.push_back({nums[i],nums[j],nums[left],nums[right]});left++;right--;while(left<right && nums[left] == nums[left-1])left++;while(left<right && nums[right] == nums[right+1])right--;}else if(sum < aim)left++;elseright--;}++j;while(j < nums.size() && nums[j] == nums[j-1])++j;}++i;while(i<nums.size() && nums[i] == nums[i-1])++i;}return vv;}
相关文章:

【算法】双指针-OJ题详解1
双指针-OJ题 移动零(点击跳转)原理讲解代码实现 复写零(点击跳转)原理讲解代码实现 快乐数(点击跳转)原理讲解代码实现 盛最多水的容器(点击跳转)原理讲解代码实现 有效三角形的个数…...

29 两个任务切换(1)
1 这里涉及到进程的切换与之前的 特权级的切换还是不一样的。 2 给每个进程 在 GDT表中,分配一个 TSS, 这个TSS中 保存着这个进程 所用到的 通用寄存器段寄存器 3个可能的栈, 当进行 进程切换的时候,就是切换到 另一个 TSS表&am…...

正则表达式概述
一、正则表达式概述 正则表达式(Regular Expression,简称regex或regexp)是一种强大的文本处理工具,它使用一种特定的模式来描述和匹配一系列符合某个句法规则的字符串。在Python中,我们可以使用re模块来操作正则表达式…...

【C语言】Top K问题【建小堆】
前言 TopK问题:从n个数中,找出最大(或最小)的前k个数。 在我们生活中,经常会遇到TopK问题 比如外卖的必吃榜;成单的前K名;各种数据的最值筛选 问题分析 显然想开出40G的空间是不现实的&#…...

Rust 程序设计语言学习——并发编程
安全且高效地处理并发编程是 Rust 的另一个主要目标。并发编程(Concurrent programming),代表程序的不同部分相互独立地执行,而并行编程(parallel programming)代表程序不同部分同时执行,这两个…...

联邦学习研究综述【联邦学习】
文章目录 0 前言机器学习两大挑战: 1 什么是联邦学习?联邦学习的一次迭代过程如下:联邦学习技术具有以下几个特点: 2 联邦学习的算法原理目标函数本地目标函数联邦学习的迭代过程 3 联邦学习分类横向联邦学习纵向联邦学习联邦迁移…...

深入理解Python中的列表推导式
深入理解Python中的列表推导式 在Python编程中,列表推导式(List Comprehension)是一种简洁而强大的语法,用于创建和操作列表。它不仅提高了代码的可读性,还能显著减少代码的行数。本文将详细介绍什么是列表推导式,如何使用它,以及一些实际应用示例,帮助读者更好地理解…...

Android 实现左侧导航栏:NavigationView是什么?NavigationView和Navigation搭配使用
目录 1)左侧导航栏效果图 2)NavigationView是什么? 3)NavigationView和Navigation搭配使用 4)NavigationView的其他方法 一、实现左侧导航栏 由于Android这边没有直接提供左侧导航栏的控件,所以我尝试了…...

如何快速下载拼多多图片信息,效率高
图片是电商吸引顾客的关键因素,高质量的商品图片能提升产品吸引力,增强用户购买欲望。良好的视觉展示有助于建立品牌形象,提高转化率。同时,图片也是商品信息的主要传递媒介,对消费者决策过程至关重要。 使用图快下载器…...

windows 10下,修改ubuntu的密码
(1)在搜索框里面输入cmd,然后点击右键,选择管理员打开 Microsoft Windows [版本 10.0.22631.3880] (c) Microsoft Corporation。保留所有权利。 C:\Windows\System32>C: C:\Windows\System32>cd ../../ C:\>cd Users\ASUS\AppData\Local\Micros…...

【MySQL】慢sql优化全流程解析
定位慢sql 工具排查慢sql 调试工具:Arthas运维工具:Skywalking 通过以上工具可以看到哪个接口比较慢,并且可以分析SQL具体的执行时间,定位到哪个sql出了问题。 启用慢查询日志 慢查询日志记录了所有执行时间超过指定参数(lon…...

RabbitMQ高级特性 - 消息分发(限流、负载均衡)
文章目录 RabbitMQ 消息分发概述如何实现消费分发机制(限制每个队列消息数量)使用场景限流背景实现 demo 非公平发送(负载均衡)背景实现 demo RabbitMQ 消息分发 概述 RabbitMQ 的队列在有多个消费者订阅时,默认会通过…...
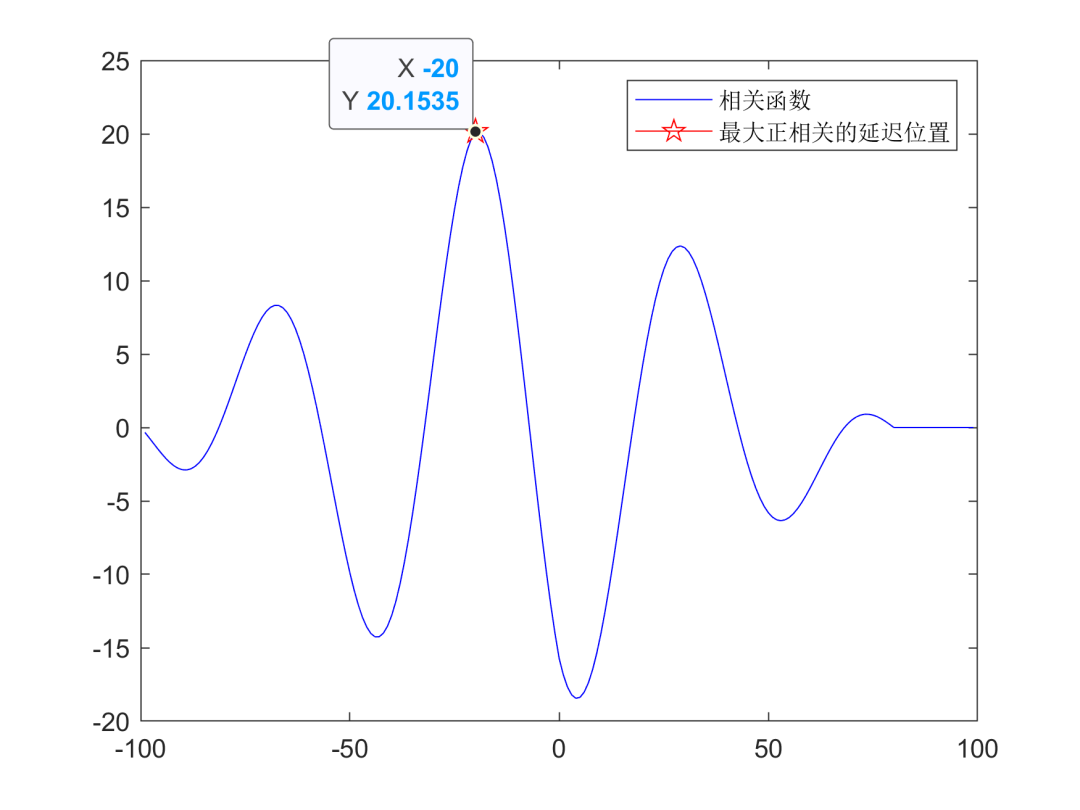
信号处理——自相关和互相关分析
1.概括 在信号处理中,自相关和互相关是相关分析非常重要的概念,它们能分析一个信号或两个信号在时间维度的相似性,在振动测试分析、雷达测距和声发射探伤得到了广泛的应用。自相关分析的研究对象为一个信号,互相关分析的研究对象…...
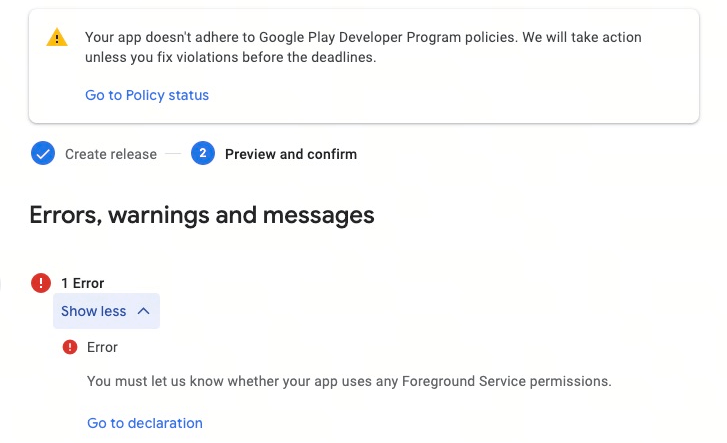
如何解决部分设备分辨率不适配
1)如何解决部分设备分辨率不适配 2)Unity中如何实现草的LOD 3)使用了Play Asset Delivery提交版本被Google报错 4)如何计算弧线弹道的落地位置 这是第396篇UWA技术知识分享的推送,精选了UWA社区的热门话题,…...

C#插件 调用存储过程(输出参数类型)
存储过程 CREATE PROCEDURE [dbo].[GetSum]num1 INT,num2 INT,result INT OUTPUT AS BEGINselect result num1 num2 END C#代码 using Kingdee.BOS; using Kingdee.BOS.App.Data; using Kingdee.BOS.Core.Bill.PlugIn; using Kingdee.BOS.Util; using System; using System.…...

代码随想录算法训练营day32 | 509. 斐波那契数 、70. 爬楼梯 、746. 使用最小花费爬楼梯
碎碎念:开始动态规划了!加油! 参考:代码随想录 动态规划理论基础 动态规划常见类型: 动规基础类题目背包问题打家劫舍股票问题子序列问题 解决动态规划问题应该要思考清楚的: 动态规划五部曲࿱…...

【人工智能专栏】Learning Rate Decay 学习率衰减
Learning Rate Decay 学习率衰减 使用格式 optimizer = torch.optim.SGD(model.paraters(), lr=0.1, momentum=0.9, weight_decay=1e-4) scheduler = torch.optim...
》题目集)
浙大版《C语言程序设计(第3版)》题目集
练习4-11 统计素数并求和 本题要求统计给定整数M和N区间内素数的个数并对它们求和。 输入格式: 输入在一行中给出两个正整数M和N(1≤M≤N≤500)。 输出格式: 在一行中顺序输出M和N区间内素数的个数以及它们的和,数字间以空格分隔。 输入…...

【学习笔记】Day 2
一、进度概述 1、inversionnet_train_light 试运行——未成功 2、DL-FWI基础入门培训-1,2,以及作业1的完成——暂未完成作业 二、详情 1、inversionnet_train_light 试运行 在补充完相关依赖后,运行仍有报错 产生原因:这个代码在当…...

Java中的Map(如果想知道Java中有关Map的知识点,那么只看这一篇就足够了!)
前言:在Java编程语言中,集合框架(Collection Framework)提供了一系列用于存储和操作数据的接口和类。其中,Map和Set是两个非常重要的接口,分别用于存储键值对和无重复元素的集合。 ✨✨✨这里是秋刀鱼不做梦…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...
