Chapter6.2:其他根轨迹及综合实例分析
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍:《MATLAB/Simulink与控制系统仿真》。
2.其他根轨迹及综合实例分析
2.1 其他形式根轨迹
2.1.1 参数根轨迹
- 除根轨迹增益K∗K^*K∗为变化参数的根轨迹外,其他情形下的根轨迹统称为广义根轨迹;如:系统的参数根轨迹,开环传递函数中零点个数多于极点个数的根轨迹,零度根轨迹;
- 将负反馈系统中K∗K^*K∗变化时的根轨迹称为常规根轨迹;
- 以非开环增益为可变参数绘制的根轨迹称为参数根轨迹;
设系统闭环特征方程为:
1+G(s)H(s)=01+G(s)H(s)=0 1+G(s)H(s)=0
进行等效变换:
AP(s)Q(s)=−1A\frac{P(s)}{Q(s)}=-1 AQ(s)P(s)=−1
其中:AAA为除K∗K^*K∗外,系统任意变化参数,P(s)、Q(s)P(s)、Q(s)P(s)、Q(s)为两个与AAA无关的首一多项式;
上两式相等,即:
Q(s)+AP(s)=1+G(s)H(s)=0Q(s)+AP(s)=1+G(s)H(s)=0 Q(s)+AP(s)=1+G(s)H(s)=0
可得等效单位系统,其等效开环传递函数为
G1(s)H1(s)=AP(s)Q(s)G_1(s)H_1(s)=A\frac{P(s)}{Q(s)} G1(s)H1(s)=AQ(s)P(s)
利用上式绘制的根轨迹就是参数AAA变化时的参数根轨迹;
2.1.2 零度根轨迹
- 如果研究的控制系统为非最小相位系统,则不能采用常规根轨迹的法则绘制系统根轨迹,其相角遵循0°+2kπ0°+2k\pi0°+2kπ条件,而不是180°+2kπ180°+2k\pi180°+2kπ条件,因此称为零度根轨迹;
- 非最小相位系统指在sss右半平面具有开环零极点的控制系统;
- 零度根轨迹来源:一是非最小相位系统中包含sss最高次幂的系数为负的因子;二是控制系统中包含正反馈内回路;
【零度根轨迹绘制法则】
-
【法则1】:根轨迹的起点和终点。
- 根轨迹起于开环极点,终于开环零点;
-
【法则2】:根轨迹的分支数、对称性和连续性。
- 根轨迹的分支数与开环有限零点数mmm和有限极点数nnn中的大者相等,根轨迹是连续且对称于实轴;
-
【法则3】:根轨迹的渐近线。
- 当开环有限极点数nnn大于有限零点数mmm时,有n−mn-mn−m条根轨迹分支沿着与实轴交角为φa\varphi_aφa、交点为σa\sigma_aσa的一组渐近线趋于无穷远处,且有:
φa=2kπn−m,k=0,1,2,⋯,n−m−1;σa=∑i=1npi−∑j=1mzjn−m\varphi_a=\frac{2k\pi}{n-m},k=0,1,2,\cdots,n-m-1;\sigma_a=\frac{\displaystyle\sum_{i=1}^np_i-\displaystyle\sum_{j=1}^mz_j}{n-m} φa=n−m2kπ,k=0,1,2,⋯,n−m−1;σa=n−mi=1∑npi−j=1∑mzj
- 当开环有限极点数nnn大于有限零点数mmm时,有n−mn-mn−m条根轨迹分支沿着与实轴交角为φa\varphi_aφa、交点为σa\sigma_aσa的一组渐近线趋于无穷远处,且有:
-
【法则4】:根轨迹在实轴上的分布。
- 实轴上的某一区域,若其右边开环实数零、极点个数之和为偶数,则该区域必是根轨迹。
-
【法则5】:根轨迹的分离点与分离角。
-
两条或两条以上根轨迹分支在sss平面上相遇又立即分开的点,称为根轨迹分离点,分离点坐标ddd:
∑j=1m1d−zj=∑i=1n1d−pi\sum_{j=1}^{m}\frac{1}{d-z_j}=\sum_{i=1}^n\frac{1}{d-p_i} j=1∑md−zj1=i=1∑nd−pi1
其中:zjz_jzj为开环零点,pip_ipi为开环极点;分离角为:(2k+1)π/l(2k+1)\pi/l(2k+1)π/l;
-
如果根轨迹位于实轴上两个相邻的开环极点间,其中一个可以是无限极点,则这两个极点间至少存在一个分离点;
-
如果根轨迹位于实轴上两个相邻的开环零点间,其中一个可以是无限零点,则这两个零点间至少存在一个分离点;
-
由两个极点和一个有限零点组成的开环系统,只要有限零点没有位于两个实数极点间,当K∗K^*K∗从零变化到无穷时,闭环根轨迹的复数部分,是以有限零点为圆心,以有限零点到分离点的距离为半径的一个圆,或圆的一部分;
-
-
【法则6】:根轨迹的起始角和终止角。
-
根轨迹离开开环复数极点处的切线与正实轴的夹角,称为起始角,记为:θpi\theta_{p_i}θpi;
-
根轨迹进入开环复数零点处的切线与正实轴的夹角,称为终止角,记为:φzi\varphi_{z_i}φzi;
-
起始角和终止角的计算:
θpi=2kπ+(∑j=1mφzjpi−∑j=1(j≠i)nθpjpi);k=0,±1,±2,⋯φzi=2kπ−(∑j=1(j≠i)mφzjzi−∑j=1nθpjzi);k=0,±1,±2,⋯\begin{aligned} &\theta_{p_i}=2k\pi+(\sum_{j=1}^m\varphi_{z_jp_i}-\sum_{j=1\\(j≠i)}^n\theta_{p_jp_i});k=0,±1,±2,\cdots\\\\ &\varphi_{z_i}=2k\pi-(\sum_{j=1\\(j≠i)}^m\varphi_{z_jz_i}-\sum_{j=1}^n\theta_{p_jz_i});k=0,±1,±2,\cdots \end{aligned} θpi=2kπ+(j=1∑mφzjpi−j=1(j=i)∑nθpjpi);k=0,±1,±2,⋯φzi=2kπ−(j=1(j=i)∑mφzjzi−j=1∑nθpjzi);k=0,±1,±2,⋯
-
-
【法则7】:根轨迹与虚轴的交点。
-
若根轨迹与虚轴相交,则交点上的K∗K^*K∗值和ω\omegaω值可用劳斯判据确定,亦可令闭环特征方程的s=jωs={\rm j}\omegas=jω,令其实部和虚部为零求解;
-
若根轨迹与虚轴相交,表示闭环系统存在纯虚根,即K∗K^*K∗的数值使闭环系统处于临界稳定状态,可令劳斯表第一列中包含K∗K^*K∗的项为零,即可确定根轨迹与虚轴交点上的K∗K^*K∗值;
-
令闭环特征方程的s=jωs={\rm j\omega}s=jω代入闭环特征方程,可得:
1+G(jω)H(jω)=01+G({\rm j}\omega)H({\rm j}\omega)=0 1+G(jω)H(jω)=0
令其实部和虚部均等于000即可求解其参数,有:
{Re[1+G(jω)H(jω)]=0Im[1+G(jω)H(jω)]=0\begin{cases} &{\rm Re}[1+G({\rm j}\omega)H({\rm j}\omega)]=0\\ &{\rm Im}[1+G({\rm j}\omega)H({\rm j}\omega)]=0 \end{cases} {Re[1+G(jω)H(jω)]=0Im[1+G(jω)H(jω)]=0
-
-
【法则8】:根之和。
- 当n−m≥2n-m≥2n−m≥2时,特征方程第二项系数与K∗K^*K∗无关,无论K∗K^*K∗取何值,开环nnn个极点之和总是等于闭环特征方程nnn个根之和,即:
∑i=1nsi=∑i=1npi\sum_{i=1}^ns_i=\sum_{i=1}^np_i i=1∑nsi=i=1∑npi
- 当n−m≥2n-m≥2n−m≥2时,特征方程第二项系数与K∗K^*K∗无关,无论K∗K^*K∗取何值,开环nnn个极点之和总是等于闭环特征方程nnn个根之和,即:
2.2 其他形式根轨迹实例
2.2.1 实例1:正反馈轨迹
实验要求:绘制正反馈系统的根轨迹,已知单位反馈系统开环传递函数G(s)H(s)=K(s+2)(s+3)(s2+2s+2),G(s)H(s)=\displaystyle\frac{K(s+2)}{(s+3)(s^2+2s+2)},G(s)H(s)=(s+3)(s2+2s+2)K(s+2),其中K<0K<0K<0,使用MATLAB{\rm MATLAB}MATLAB绘制系统的根轨迹。
解:
% 实例Chapter6.2.2.1
clc;clear;% 建立控制系统模型
num=[1,2];den=conv([1,3],[1,2,2]);
sys=tf(num,den);% 绘制根轨迹
rlocus(-sys);axis([-10 5 -3 3]);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('正反馈根轨迹图','FontSize',15);

2.2.2 实例2:参数根轨迹
实验要求:已知某单位负反馈系统开环传递函数为:G(s)H(s)=5(s+a)(s+1)(s+3)(s+12)G(s)H(s)=\displaystyle\frac{5(s+a)}{(s+1)(s+3)(s+12)}G(s)H(s)=(s+1)(s+3)(s+12)5(s+a),其中:2≤a≤102≤a≤102≤a≤10,使用MATLAB{\rm MATLAB}MATLAB绘制参数aaa的根轨迹。
解:
% 实例Chapter6.2.2.2
clc;clear;% 定义变量
K=5;den=conv([1,1],conv([1,3],[1,12]));% 定义数组存储结果
clpoles=[];param=[];% a值从2变化到10
for a=2:10num=[0,0,K,K*a];clpoly=num+den;clp=roots(clpoly);clpoles=[clpoles;clp'];param=[param;a];
end% 打印a和极点表格
disp([param,clpoles]);% 绘制极点
plot(clpoles,'*');
axis equal;axis([-4,0,-2,2]);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('参数根轨迹','FontSize',15);
% 极点表格:2.0000 + 0.0000i -11.4658 + 0.0000i -3.3291 + 0.0000i -1.2051 + 0.0000i3.0000 + 0.0000i -11.5249 + 0.0000i -3.0000 + 0.0000i -1.4751 + 0.0000i4.0000 + 0.0000i -11.5826 + 0.0000i -2.4174 + 0.0000i -2.0000 + 0.0000i5.0000 + 0.0000i -11.6388 + 0.0000i -2.1806 - 0.6972i -2.1806 + 0.6972i6.0000 + 0.0000i -11.6938 + 0.0000i -2.1531 - 1.0041i -2.1531 + 1.0041i7.0000 + 0.0000i -11.7475 + 0.0000i -2.1262 - 1.2341i -2.1262 + 1.2341i8.0000 + 0.0000i -11.8001 + 0.0000i -2.1000 - 1.4251i -2.1000 + 1.4251i9.0000 + 0.0000i -11.8516 + 0.0000i -2.0742 - 1.5913i -2.0742 + 1.5913i10.0000 + 0.0000i -11.9020 + 0.0000i -2.0490 - 1.7399i -2.0490 + 1.7399i

2.2.3 实例3:延迟系统根轨迹
实验要求:已知某单位负反馈系统的开环传递函数为:G(s)H(s)=1s(s+1)(0.5s+1)e−sG(s)H(s)=\displaystyle\frac{1}{s(s+1)(0.5s+1)}{\rm e}^{-{s}}G(s)H(s)=s(s+1)(0.5s+1)1e−s,使用MATLAB{\rm MATLAB}MATLAB绘制该延迟系统的根轨迹。
解:
% 实例Chapter6.2.2.3
clc;clear;% 建立控制系统模型
num=[0,1];den=conv([1,0],conv([1,1],[0.5,1]));
sys1=tf(num,den);% 对延迟环节进行Pade近似
[np,dp]=pade(1,3);
sys=sys1*tf(np,dp);% 绘制根轨迹
rlocus(sys);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('延迟系统根轨迹图','FontSize',15);

2.3 控制系统性能分析
2.3.1 闭环零极点与时间响应
- 系统的动态性能基本上由接近虚轴的闭环极点确定,这样的极点,称为主导极点;
- 主导极点定义为对整个时间响应过程起主要作用的闭环极点;
- 时间响应分量的消逝速度,除取决于相应闭环极点的实部值外,还与该极点处的留数,即闭环零、极点之间的相互位置有关;
- 只有既接近虚轴,又不十分接近闭环零点的闭环极点,才可能成为主导极点;
- 如果闭环零、极点相距很近,那么这样的闭环零、极点常称为偶极子;偶极子有实数偶极子和复数偶极子之分,复数偶极子必共轭出现;只要偶极子不十分接近坐标原点,它们对系统的影响甚微,可以忽略它们的存在;
- 接近坐标原点的偶极子对系统动态性能的影响必须考虑;不论偶极子接近坐标原点的程度如何,并不影响系统主导极点的地位;
- 确定偶极子法则:如果闭环零、极点之间的距离比它们本身模值小一个数量级,则这一对闭环零、极点就构成偶极子;
- 采用主导极点代替系统全部闭环极点来估算系统性能指标的方法,称为主导极点法;采用主导极点时,在全部闭环极点中,选留最靠近虚轴而又不十分靠近闭环零点的一个或几个闭环极点作为主导极点,略去不十分接近原点的偶极子,以及比主导极点距虚轴远六倍以上的闭环零、极点;
2.3.2 系统性能定性分析
闭环系统零、极点位置对时间响应性能的影响总结:
- 稳定性。如果闭环极点全部位于sss左半平面,则系统一定是稳定的,即稳定性只与闭环极点位置有关,与闭环零点无关;
- 运动形式。如果闭环系统无零点,且闭环极点均为实数极点,则时间响应一定是单调的;如果闭环极点均为复数极点,则时间响应一般是振荡的;
- 超调量。超调量主要取决于闭环复数主导极点的衰减率σ1/ωd=ζ/1−ζ2\sigma_1/\omega_d=\zeta/\sqrt{1-\zeta^2}σ1/ωd=ζ/1−ζ2,并与其他闭环零、极点接近坐标原点的程度有关;
- 调节时间。调节时间主要取决于最靠近虚轴的闭环复数极点的实部绝对值σ1=ζωn\sigma_1=\zeta\omega_nσ1=ζωn;如果实数极点距虚轴最近,且附近没有实数零点,则调节时间主要取决于该实数极点的模值;
- 实数零、极点影响。零点减小系统阻尼,使峰值时间提前,超调量增大;极点增大系统阻尼,使峰值时间滞后,超调量减小;它们的作用,随着本身接近坐标原点的程度而加强;
- 偶极子及其处理。如果零、极点之间的距离比它们本身的模值小一个数量级,则构成偶极子;远离原点的偶极子影响可忽略,接近原点的偶极子影响必须考虑;
- 主导极点。在sss平面上,最靠近虚轴而附近没有闭环零点的一些闭环极点,对系统性能影响最大,称为主导极点;凡比主导极点实部大3~6倍以上的其他闭环零、极点影响可忽略;
- 闭环实数主导极点对系统性能的影响:闭环实数主导极点作用相当于增大系统的阻尼,使峰值时间滞后,超调量下降;如果实数极点比共轭复数极点更接近坐标原点,甚至可以使振荡过程变为非振荡过程;
2.4 综合实例分析
实验要求:已知单位负反馈控制系统开环传递函数为:G(s)H(s)=K(s+1)s(s−1)(s+4)G(s)H(s)=\displaystyle\frac{K(s+1)}{s(s-1)(s+4)}G(s)H(s)=s(s−1)(s+4)K(s+1),要求:
- 绘制此控制系统的根轨迹;
- 确定使闭环系统稳定的KKK值;
- 分析此控制系统的阶跃响应性能;
- 利用rltool{\rm rltool}rltool对系统的性能进行分析;
解:
【STEP1{\rm STEP1}STEP1】:建立此控制系统的数学模型。
% STEP1:建立控制系统的模型
num=[1,1];den=conv([1,0],conv([1,-1],[1,4]));
sys=tf(num,den);sys
% 控制系统模型输出:
sys = s + 1-----------------s^3 + 3 s^2 - 4 s
【STEP2{\rm STEP2}STEP2】:绘制该控制系统根轨迹。
% STEP2:绘制控制系统根轨迹
rlocus(sys);grid on;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统根轨迹图','FontSize',15);% 计算用户选定点处的增益和其他闭环极点
[k,poles]=rlocfind(sys)
% 在根轨迹图上点击根轨迹与虚轴交点,输出如下:
k =6.0267poles =-2.9951 + 0.0000i-0.0024 + 1.4185i-0.0024 - 1.4185i

- 当增益K>6K>6K>6时,闭环控制系统所有极点均位于虚轴的左半部分,此时系统稳定;
【STEP3{\rm STEP3}STEP3】:使用rltool{\rm rltool}rltool工具分析。
% STEP3:使用rltool工具分析
rltool(sys)% 在rltool工具中,设置C的值为6
% New Plot中选择绘制STEP响应
【K=6K=6K=6阶跃响应】

【K=20K=20K=20阶跃响应】

相关文章:

Chapter6.2:其他根轨迹及综合实例分析
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。 自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468…...
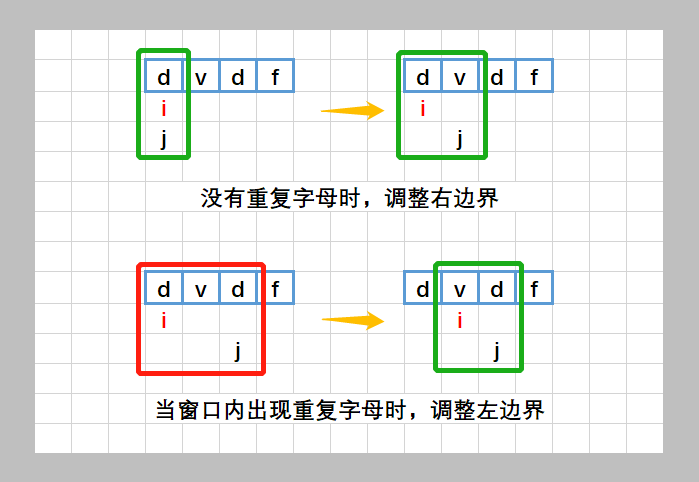
3. 无重复字符的最长子串——滑动窗口
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2: 输入: s "bbbbb" 输出: 1 解释: 因为无…...
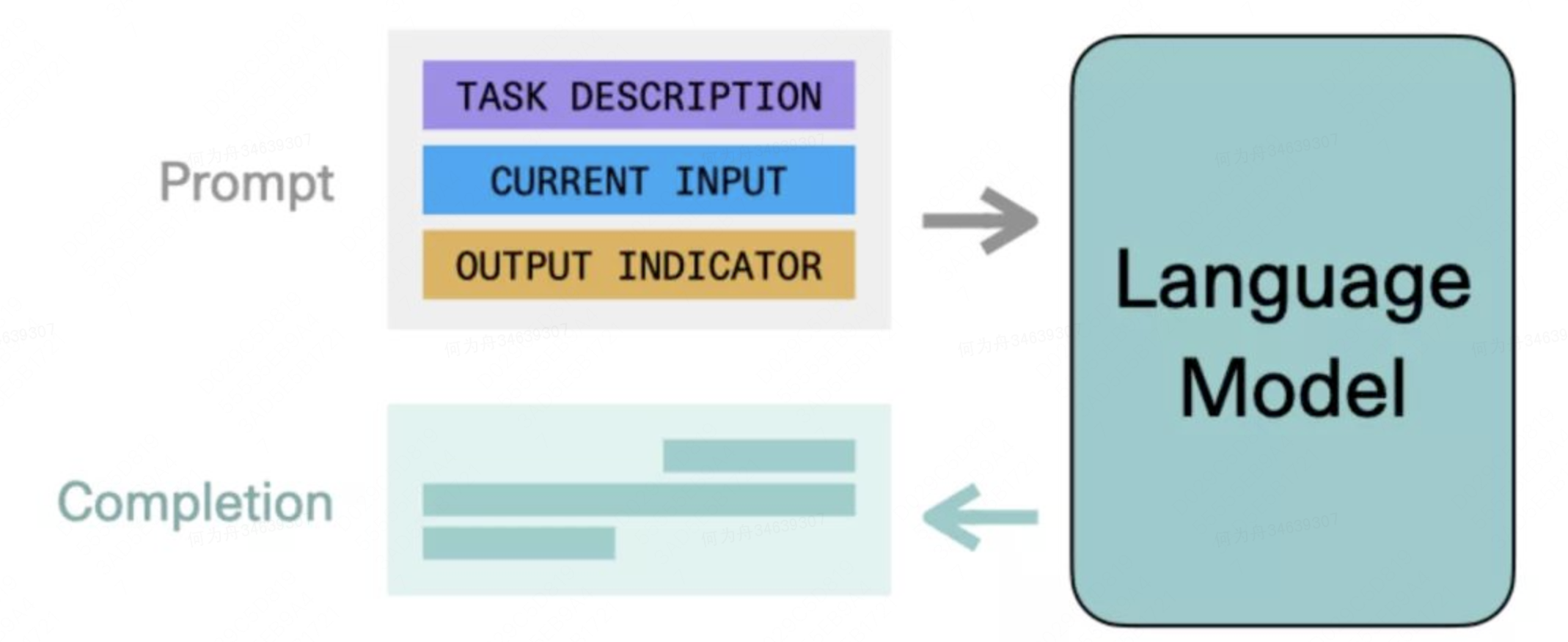
ChatGPT研究分享:机器第一次开始理解人类世界
0、为什么会对ChatGPT感兴趣一开始,我对ChatGPT是没什么关注的,无非就是有更大的数据集,完成了更大规模的计算,所以能够回答更多的问题。但后来了解到几个案例,开始觉得这个事情并不简单。我先分别列举出来,…...

可换皮肤的Qt登录界面
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三连支持一下呗。👍⭐️❤️ 可换皮肤的Qt登录界面 QSS的学习笔记 快…...

Spring的常见问题汇总
一、bean实例化1、构造方法底层是无参构造方法来new的对象。2、静态工厂实例化Bean实质上就是:创建一个静态工厂类,然后调用静态工厂类的静态方法,来创建对象。3、实例工厂与FactoryBean实质上就是:创建一个工厂类,工厂…...
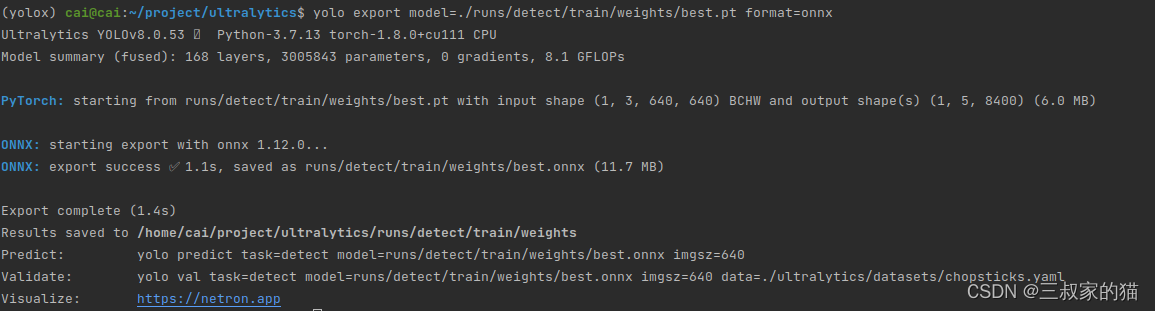
yolov8训练筷子点数数据集
序言 yolov8发布这么久了,一直没有机会尝试一下,今天用之前自己制作的筷子点数数据集进行训练,并且记录一下使用过程以及一些常见的操作方式,供以后翻阅。 一、环境准备 yolov8的训练相对于之前的yolov5简单了很多,…...
使用 Python 从点云生成 3D 网格
从点云生成 3D 网格的最快方法 已经用 Python 编写了几个实现来从点云中获取网格。它们中的大多数的问题在于它们意味着设置许多难以调整的参数,尤其是在不是 3D 数据处理专家的情况下。在这个简短的指南中,我想展示从点云生成网格的最快和最简单的过程。…...
将字符串分割数组join()将数组转字符串reverse()将数组反转)
vue使用split()将字符串分割数组join()将数组转字符串reverse()将数组反转
1.split() 将字符串切割成数组 const str Hello Vue2 Vue3 console.log(str.split()) console.log(str.split()) console.log(str.split( )) console.log(str.split( , 2)) console.log(str.split( , 6))输出如下 1.split()不传参数默认整个字符串作为数组的一个元素…...
队列实现及leetcode相关OJ题
上一篇写的是栈这一篇分享队列实现及其与队列相关OJ题 文章目录一、队列概念及实现二、队列源码三、leetcode相关OJ一、队列概念及实现 1、队列概念 队列同栈一样也是一种特殊的数据结构,遵循先进先出的原则,例如:想象在独木桥上走着的人&am…...
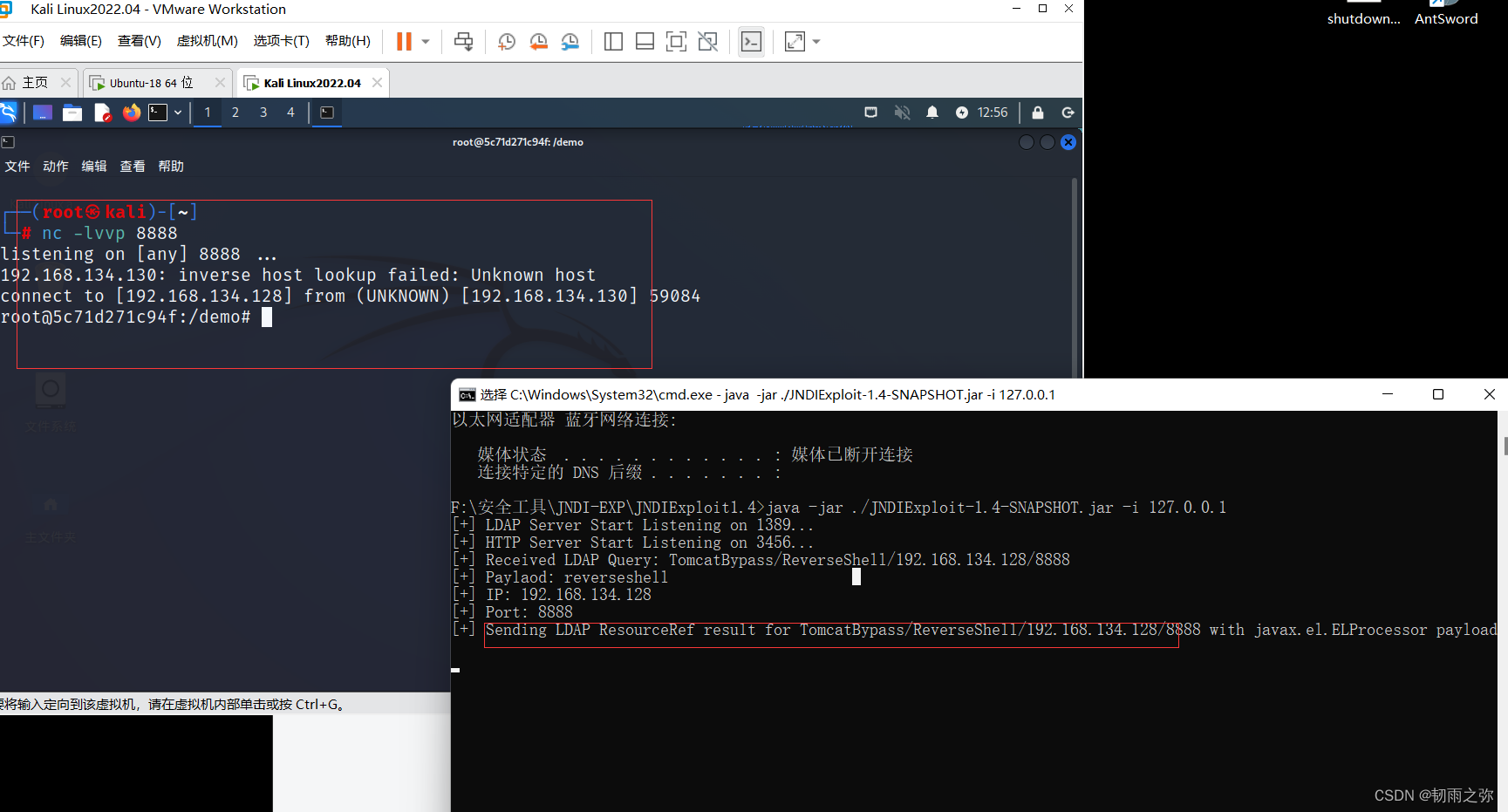
【Log4j2远程命令执行复现CVE-2021-12-09】
目录 一、前言 二、漏洞环境构建 三、复现过程 一、前言 Log4j2是基于log4j这个java日志处理组件进行二次开发和改进而来的。也是目前最常用的日志框架之一,在之前的博客中(http://t.csdn.cn/z9um4)我们阐述了漏洞的原理和大致的利用方…...
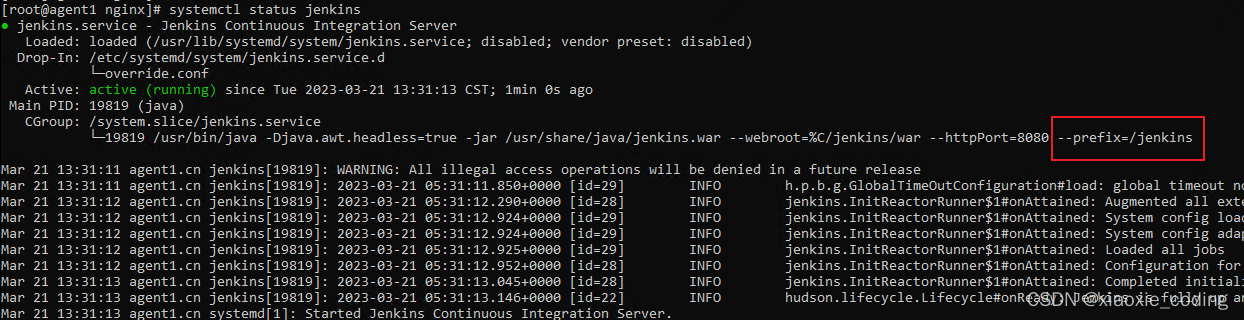
Jenkins 平台搭建 | 为 Jenkins 配置 nginx 反向代理
以 Centos7 系统为例,详细记录一下 Jenkins 搭建流程。 参考官网:https://www.jenkins.io/doc/book/installing/linux/#red-hat-centos Install Jenkins 从 redhat-stable yum 存储库中安装 LTS(长期支持) 版本,该版…...

【云原生】Docker 架构及工作原理
一、Docker 概述二、Client 客户端三、Docker 引擎四、Image 镜像五、Container 容器六、镜像分层可写的容器层七、Volume 数据卷八、Registry 注册中心九、总结一、Docker 概述 Docker 是一个开发、发布和运行应用程序的开放平台。Docker使您能够将应用程序与基础架构分离&am…...
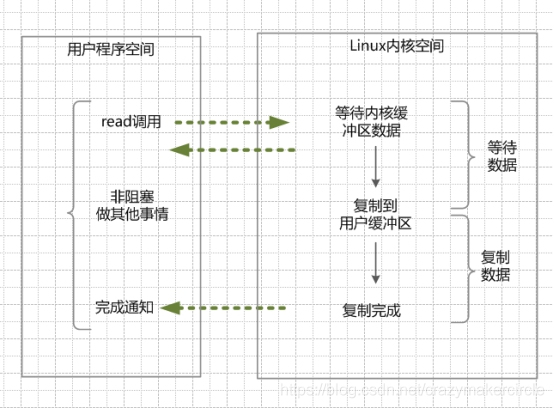
【Java 】Java NIO 底层原理
文章目录1、 Java IO读写原理1.1 内核缓冲与进程缓冲区1.2 java IO读写的底层流程2、 四种主要的IO模型3、 同步阻塞IO(Blocking IO)4、 同步非阻塞NIO(None Blocking IO)5、 IO多路复用模型(I/O multiplexing)6、 异步…...

Vue基础27之VueUI组件
Vue基础27Vue UI组件库移动端常用 UI 组件库PC 端常用 UI 组件库Element-ui插件基本使用安装引入并使用main.jsApp.vue按需引入安装 babel-plugin-componentbabel.config.jsmain.jsApp.vueVue UI组件库 移动端常用 UI 组件库 Vant https://youzan.github.io/vant Cube UI htt…...

第35篇:Java代码规范全面总结
编程规范目的是帮助我们编写出简洁、可维护、可靠、可测试、高效、可移植的代码,提高产品代码的质量。 适当的规范和标准绝不是消灭代码内容的创造性、优雅性,而是限制过度个性化, 以一种普遍认可的统一方式一起做事,提升协作效率,降低沟通成本。 代码的字里行间流淌的是软…...

Cookie和Session详解
目录 前言: Session详解 Cookie和Session区别和关联 服务器组织会话的方式 使用Tomcat实现登录成功跳转到欢迎页面 登录前端页面 登录成功后端服务器 重定向到欢迎页面 抓包分析交互过程 小结: 前言: Cookie之前博客有介绍过&#x…...
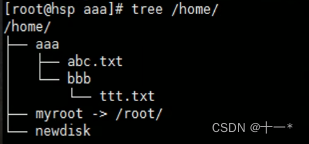
Linux之磁盘分区、挂载
文章目录一、Linux分区●原理介绍●硬盘说明查看所有设备挂载情况挂载的经典案例二、磁盘情况查询基本语法应用实例磁盘情况-工作实用指令一、Linux分区 ●原理介绍 Linux来说无论有几个分区,分给哪一目录使用,它归根结底就只有一个根目录,…...
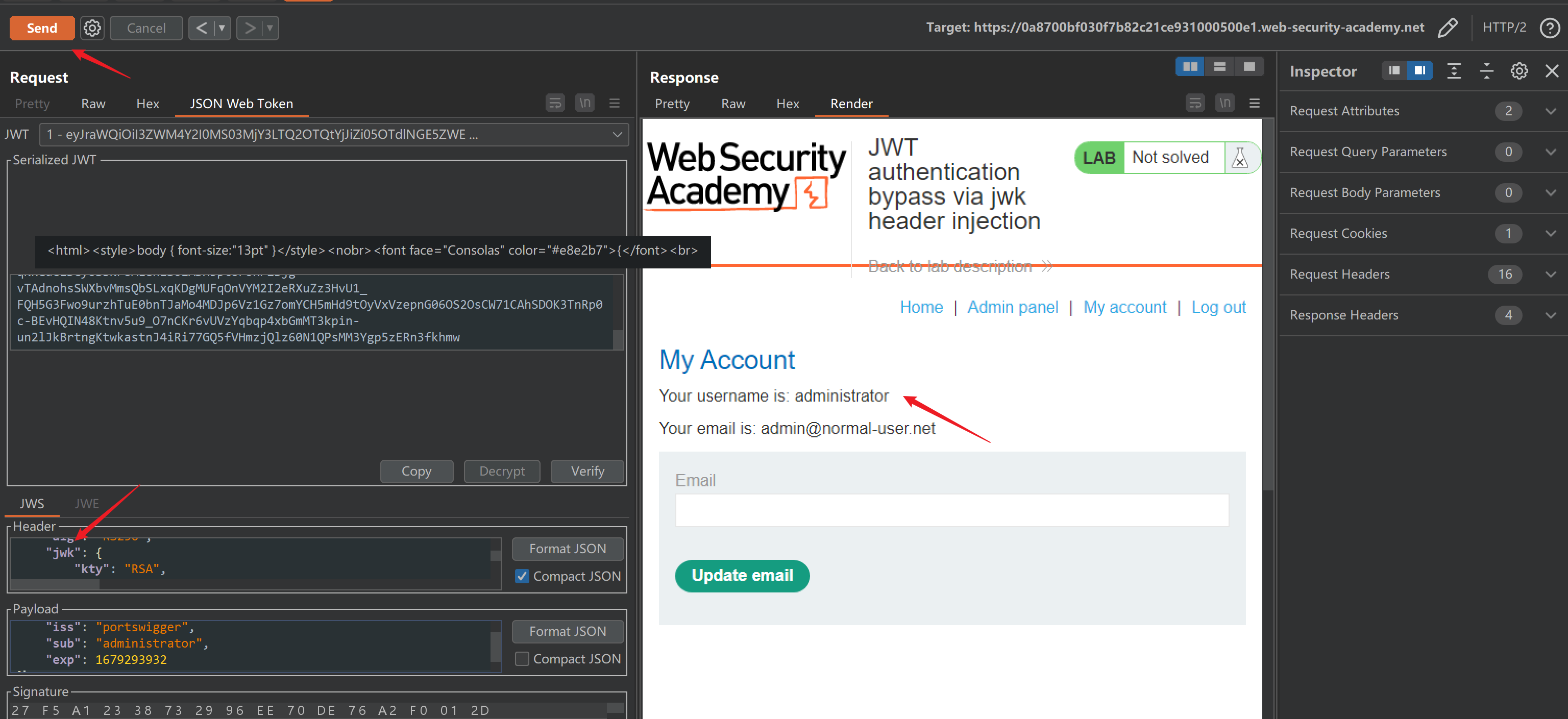
web渗透之jwt 安全问题
前言JWT 全称 JSON Web Token,是一种标准化格式,用于在系统之间发送加密签名的 JSON 数据。原始的 Token 只是一个 uuid,没有任何意义。JWT 包含了部分业务信息,减少了 Token 验证等交互操作,效率更高JWT组成JWT 由三部…...

好用的5款国产低代码平台介绍
一、云程低代码平台 云程低代码平台是一款基于springboot、vue.js技术的企业级低代码开发平台,平台采用模型驱动、高低码融合、开放扩展等设计理念,基于业务建模、流程建模、表单建模、报表建模、大屏建模等可视化建模工具,通过拖拉拽零代码方…...

【前端学习记录】webpack学习之mini-css-extract-plugin插件
前言 最近在学习尚硅谷的webpack5课程,看到mini-css-extract-plugin这个插件的时候,感觉很有帮助,之前都没有在css这方面深入思考过,课程中的一些记录写在下面 为什么需要优化CSS Css 文件目前被打包到 js 文件中,当…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
