llama神经网络的结构,llama-3-8b.layers=32 llama-3-70b.layers=80; 2000汉字举例说明
目录
llama-3-8b.layers=32 llama-3-70b.layers=80
llama神经网络的结构
Llama神经网络结构示例
示例中的输入输出大小
实际举例说明2000个汉字文本数据集
初始化词嵌入矩阵
1. 输入层
2. 嵌入层
3. 卷积层
4. 全连接层

llama-3-8b.layers=32 llama-3-70b.layers=80
shard_mappings = {"llama-3-8b": {"MLXDynamicShardInferenceEngine": Shard(model_id="mlx-community/Meta-Llama-3-8B-Instruct-4bit", start_layer=0, end_layer=0, n_layers=32),"TinygradDynamicShardInferenceEngine": Shard(model_id="llama3-8b-sfr", start_layer=0, end_layer=0, n_layers=32),},"llama-3-70b": {"MLXDynamicShardInferenceEngine": Shard(model_id="mlx-community/Met相关文章:

llama神经网络的结构,llama-3-8b.layers=32 llama-3-70b.layers=80; 2000汉字举例说明
目录 llama-3-8b.layers=32 llama-3-70b.layers=80 llama神经网络的结构 Llama神经网络结构示例 示例中的输入输出大小 实际举例说明2000个汉字文本数据集 初始化词嵌入矩阵 1. 输入层 2. 嵌入层 3. 卷积层 4. 全连接层 llama-3-8b.layers=32 llama-3-70b.laye…...

单细胞数据怎么表现genes mRNA表达的热图?
愿武艺晴小朋友一定得每天都开心 #热图 library("ComplexHeatmap") exp <- AverageExpression(subset(fasting_memory, Celltype %in% c("Pre-B")), layer = "data", #即CPM值 features …...

Java聚合快递对接云洋系统小程序源码
🚀【物流新纪元】聚合快递如何无缝对接云洋系统,效率飙升秘籍大公开!✨ 🔍 开篇揭秘:聚合快递的魅力所在 Hey小伙伴们,你是否还在为多家快递公司账号管理繁琐、订单处理效率低下而头疼?&#…...
修改数据表)
MySQL——数据表的基本操作(三)修改数据表
有时候,希望对表中的某些信息进行修改,这时就需要修改数据表。所谓修改数据表指的是修改数据库中已经存在的数据表结构,比如,修改表名、修改字段名、修改字段的数据类型等。在 MySQL中,修改数据表的操作都是使用 ALTER…...

医学图像分割的基准:TransUnet(用于医学图像分割的Transformer编码器)器官分割
1、 TransUnet 介绍 TransUnet是一种用于医学图像分割的深度学习模型。它是基于Transformer模型的图像分割方法,由AI研究公司Hugging Face在2021年提出。 医学图像分割是一项重要的任务,旨在将医学图像中的不同结构和区域分离出来,以便医生可…...

java-swing编写学生成绩查询管理系统
本文是本人大二上实训项目-学生成绩查询管理系统,采用本项目使用Java、MySQL技术。界面框架由Java Swing搭建,用JDBC实现Java与MySQL的连接。 本项目适合初学java和mysql的同学,来做一些小项目来提升自己,因为兴趣所以想要做去尝…...

volatile浅解
volatile修饰的变量有两个特点 线程中修改了自己工作内存中的副本后,立即将其刷新到主内存工作内存中每次读取共享变量时,都会去主内存中重新读取,然后拷贝到工作内存 内存 -> CPU Cache -> CPU 如果没有volatile那么就会继续读取缓存…...

世媒讯带您了解什么是媒体邀约
什么是媒体邀约?其实媒体邀约是一种公关策略,旨在通过邀请媒体记者和编辑参加特定的活动、发布会或其他重要事件,以确保这些活动能够得到广泛的报道和关注。通过这种方式,企业和组织希望能够传达重要信息,提高品牌知名…...

[Kimi 笔记]“面向搜索引擎”
"面向搜索引擎"(Search Engine-Oriented,SEO-Oriented 或 SEO-Friendly)通常指的是在设计和开发网站时,采取一系列措施来优化网站内容和结构,以便提高网站在搜索引擎结果页面(SERP)中…...

如何在亚马逊云科技AWS上利用LoRA高效微调AI大模型减少预测偏差
简介: 小李哥将继续每天介绍一个基于亚马逊云科技AWS云计算平台的全球前沿AI技术解决方案,帮助大家快速了解国际上最热门的云计算平台亚马逊云科技AWS AI最佳实践,并应用到自己的日常工作里。 在机器学习和人工智能领域,生成偏差…...

订单定时状态处理业务(SpringTask)
文章目录 概要整体架构流程技术细节小结 概要 订单定时状态处理通常涉及到对订单状态进行定期检查,并根据订单的状态自动执行某些操作,比如关闭未支付的订单、自动确认收货等. 需求分析以及接口设计 需求分析 用户下单后可能存在的情况: …...

STM32 | ADC+RS485(第十天)
点击上方"蓝字"关注我们 01、ADC概述 ADC, Analog-to-Digital Converter的缩写,指模/数转换器或者模拟/数字转换器。是指将连续变量的模拟信号转换为离散的数字信号的器件。真实世界的模拟信号.例如温度、压力、声音或者图像等,需要转换成更容易储存、处理和发射的…...

python打包成能够在mac里面运行的程序
要将你的PyQt5应用程序打包成可以在macOS上运行的独立应用程序,可以使用工具如PyInstaller或py2app。下面是使用py2app的详细步骤,因为它是macOS上专用的打包工具,并且更好地支持PyQt5。 1. 安装py2app 首先,确保你的macOS系统上…...
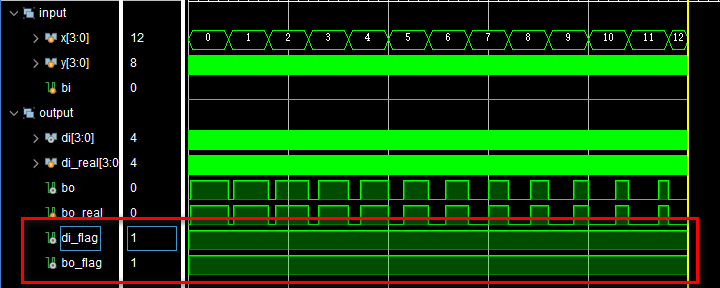
基于FPGA的数字信号处理(20)--半减器和全减器
目录 1、前言 2、半减器 3、全减器 4、减法器 文章总目录点这里:《基于FPGA的数字信号处理》专栏的导航与说明 1、前言 既然有半加器和全加器,那自然也有半减器和全减器了。尽管在电路中减法的实现基本都是 补码 加法 的形式,但是正所谓…...

Python:单引号,双引号,三引号的区别
在Python中,单引号()、双引号(")和三引号( 或 """)都可以用来定义字符串,但它们之间有一些区别: 单引号()和双引号…...

电子电气架构 ---SOMEIP/SD初入门
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

一些数学基础概念
一些数学基础概念 概率密度函数(PDF) 概率密度函数(Probability Density Function,简称 PDF)是描述连续随机变量的概率分布的一种函数。它用来表示随机变量在各个取值区间内的概率密度。 1. 定义 对于一个连续随机变量 ( X ),…...

责任有限公司的一般组织结构
责任有限公司(有限责任公司,LLC)的组织结构通常是为了确保公司运营的有效性和管理的透明度。以下是一般责任有限公司的组织结构及其主要组成部分: 1. 股东(Shareholders) 职责和角色 所有者:…...

Leetcode3227. 字符串元音游戏
Every day a Leetcode 题目来源:3227. 字符串元音游戏 解法1:博弈论 分类讨论: 如果 s 不包含任何元音,小红输。如果 s 包含奇数个元音,小红可以直接把整个 s 移除,小红赢。如果 s 包含正偶数个元音&am…...

网络流量分析在运维管理中的重要性与实施策略
在运维管理工作中,网络流量分析是一项不可或缺的技术手段。通过对网络流量的深入剖析,运维团队能够更全面地了解网络状态,及时发现潜在问题,优化网络性能,从而确保企业网络的稳定与高效运行。本文将详细探讨网络流量分…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...
