svd在求解最小二乘中的应用
文章目录
- 线性最小二乘的直接解法(正规方程解法)
- 什么是伪逆?
- 伪逆矩阵的一般形式
- 伪逆矩阵与SVD的关系
线性最小二乘的直接解法(正规方程解法)
对于 A x = b \boldsymbol{A}x=b Ax=b的线性最小二乘问题,有直解析解: x = ( A T A ) − 1 A T b x=(A^{\mathrm{T}}A)^{-1}A^{\mathrm{T}}b x=(ATA)−1ATb
什么是伪逆?
对于正方形满秩矩阵而言存在逆矩阵,但是对于非正方形矩阵(行列数量不等)或者秩亏矩阵而言,若 A + A^{+} A+满足以下四个条件:
A A + A = A . A A^{+} A=A \text {. } AA+A=A.
A + A A + = A + . A^{+} A A^{+}=A^{+} \text {. } A+AA+=A+.
( A A + ) T = A A + . \left(A A^{+}\right)^T=A A^{+} . (AA+)T=AA+.
( A + A ) T = A + A \left(A^{+} A\right)^T=A^{+} A (A+A)T=A+A
则称 A + A^{+} A+为矩阵 A A A的伪逆矩阵,也称为Moore–Penrose 逆矩阵。
伪逆矩阵的一般形式
- 当 A A A 是列满秩矩阵时有:
A + = ( A T A ) − 1 A T . A^{+}=\left(A^T A\right)^{-1} A^T \text {. } A+=(ATA)−1AT.
此时称为左伪逆矩阵,此时满足 A + A = I A^{+} A=I A+A=I.
- 当 A A A 是行满秩矩阵(秩亏)时有:
A + = A ∗ ( A A ∗ ) − 1 . A^{+}=A^*\left(A A^*\right)^{-1} \text {. } A+=A∗(AA∗)−1.
此时称为右伪逆矩阵,此时满足 A A + = I A A^{+}=I AA+=I.
可以发现伪逆的一般形式与线性最小二乘的直接解法形式相同(二者相差右乘系数b)
伪逆矩阵与SVD的关系
由 A A A 的奇异值分解性质可知: ( A T A ) V = Σ 2 V 得: ( A T A ) = V Σ 2 V − 1 \left(A^T A\right)V=\Sigma^{2}V得: \left(A^T A\right)=V\Sigma^{2}V^{-1} (ATA)V=Σ2V得:(ATA)=VΣ2V−1
因为: A T = ( V T ) T Σ T U T = V Σ T U T A^{\mathrm{T}}=\left(V^{\mathrm{T}}\right)^{\mathrm{T}} \Sigma^{\mathrm{T}} U^{\mathrm{T}}=V \Sigma^{\mathrm{T}} U^{\mathrm{T}} AT=(VT)TΣTUT=VΣTUT.
U , V U,V U,V为正交矩阵,所以:
U T = U − 1 , V T = V − 1 U^T=U^{-1},V^T=V^{-1} UT=U−1,VT=V−1
- 当 A A A 是列满秩矩阵时(参数数量小于方程数量,此时有最小二乘解)有:
A + = ( A T A ) − 1 A T = ( V Σ 2 V − 1 ) − 1 V Σ U − 1 = V Σ − 1 U T A^{+}=\left(A^T A\right)^{-1} A^T =(V\Sigma^{2}V^{-1})^{-1}V \Sigma U^{-1} =V \Sigma^{-1} U^{T} A+=(ATA)−1AT=(VΣ2V−1)−1VΣU−1=VΣ−1UT
可以发现:利用SVD分解可以求解线性最小二乘问题。此外可以发现 Σ \Sigma Σ(奇异值)对于解的稳定性(是否是病态方程组)至关重要。特别地,当 A A A为满秩方阵时,奇异值最大值与最小值的比值为矩阵 A A A的条件数,条件数反应了矩阵 A A A元素对方程解稳定性的影响程度。
参考
1
《线性代数及其应用》7.4
2
3
4
华东师范大学:第三讲线性最小二乘问题
相关文章:

svd在求解最小二乘中的应用
文章目录 线性最小二乘的直接解法(正规方程解法)什么是伪逆?伪逆矩阵的一般形式伪逆矩阵与SVD的关系 线性最小二乘的直接解法(正规方程解法) 对于 A x b \boldsymbol{A}xb Axb的线性最小二乘问题,有直解析…...

JVM—垃圾收集算法和HotSpot算法实现细节
参考资料:深入理解Java虚拟机:JVM高级特性与最佳实践(第3版)周志明 1、分代回收策略 分代的垃圾回收策略,是基于这样一个事实:不同的对象的生命周期是不一样的。因此,不同生命周期的对象可以采取…...

nvidia系列教程-AGX-Orin基础环境搭建
目录 前言 一、Agx-Orin(32GB)介绍 1.1 GPU 1.2 CPU 1.3 NVDLA 1.4 内存 1.5 存储 二、安装JetPack SDK 三、基础环境配置 四、jetpack软件版本 总结 前言 NVIDIA Jetson AGX Orin 是一款功能强大的嵌入式AI平台,专为需要高性能和低…...

使用SpringAOP实现公共字段填充
文章目录 概要整体架构流程技术细节小结 概要 在新增员工或者新增菜品分类时需要设置创建时间、创建人、修改时间、修改人等字段,在编辑员工或者编辑菜品分类时需要设置修改时间、修改人等字段。这些字段属于公共字段,也就是也就是在我们的系统中很多表…...

c++初阶-----适配器---priority_queue
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...

VSCode上安装C#环境教程
本章教程,教你如何在vscode上,可以快速运行一些基础的c#代码。 1、下载 .NET Code SDK 下载地址:https://dotnet.microsoft.com/zh-cn/download/dotnet/sdk-for-vs-code?utm_source=vs-code&utm_medium=referral&utm_campaign=sdk-install 根据自己的操作系统,选择…...

VS Code 和 Visual Studio 哪个更好
文章目录 VS Code 和 Visual Studio 哪个更好Visual Studio Code简介Visual Studio简介相同点差异点总结 VS Code 和 Visual Studio 哪个更好 Visual Studio Code简介 Visual Studio Code(简称 VS Code)是一款开源的、免费的、跨平台的、轻量级的代码编…...

FCA-数据分析理论试卷
其他参考: https://segmentfault.com/a/1190000043363073 https://blog.csdn.net/CSDN_WYY/article/details/137082340 Part.1:判断题(总分:8分 得分:8) 第1题 判断题 对任意事件A和B,必有 …...

WPF程序通过CadLib4加载CAD .dwg格式文件
1、下载CadLib相关dll文件,主要用到的:WW.dll、WW.Cad.dll、WW.GL.dll 2、程序中引用dll库。 3、创建WPF程序,使用Canvas来加载dwg文件,支持拖动和放大缩小。 4、部分代码: public void Init(string filename) {tr…...

图表全能王(ChartStudio) 上架VisionPro!
图表全能王(ChartStudio) - 终极图表制作工具!支持条形图、折线图、面积图、柱形图、条形图、饼图、玫瑰图、雷达图、牛肉图、风琴图、旭日图、桑基图等图表。 https://apps.apple.com/app/chartstudio-data-analysis/id6474099675 https://apps.apple.com/cn/app/…...

【云原生】Job一次性任务详解
Job一次性任务 文章目录 Job一次性任务一、Job介绍二、运行示例Job 一、Job介绍 Job会创建一个或者多个Pod,并将继续重试Pod的执行,直到指定数量的Pod成功终止。随着Pod成功借宿,Job跟踪记录成功完成的Pod个数。当数量达到指定的成功个数阈值…...

化工厂人员定位采用多种定位技术的融合定位系统的好处
由于化工厂内环境的复杂性和危险性,通常单一的定位技术很难满足全厂区的人员定位需求,如果能将不同定位技术融合在一起,发挥出它们各自的优势,那么就能解决以上问题。 融合定位技术诞生背景 随着科技的不断发展,多种定…...

使用AI绘图工具生成风景图像的教程
随着人工智能技术的飞速发展,AI绘图工具在图像生成和艺术创作方面变得越来越强大,无论你是一个设计师、艺术家,还是仅仅对生成艺术感兴趣的爱好者,AI绘图工具都可以帮助你轻松地创作出惊艳的风景图像。 在这篇教程中,…...

迷你主机:华硕PN65和nuc13pro如何选择?
华硕PN65与NUC 13 Pro:如何做出选择? 在追求高效能与便携性的今天,迷你主机成为了越来越多用户的选择。华硕PN65与英特尔NUC 13 Pro作为市场上两款备受瞩目的产品,各自拥有独特的优势和特点。本文将从处理器性能、扩展性、接口丰…...
分享一个好用的印花重绘工具
本文向大家介绍一款革命性的 AI 工具,它能够将模糊不清的图片转化为具有照片级别的高清图像。这项前沿项目依托于大规模人工智能技术,革新了图像恢复领域。通过文本驱动和智能修复功能,它巧妙地结合了先进的 AI 技术与创新理念,为…...
)
力扣题解(递增的三元子序列)
334. 递增的三元子序列 给你一个整数数组 nums ,判断这个数组中是否存在长度为 3 的递增子序列。 如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ,使得 nums[i] < nums[j] < nums[k] ,返回 true ;否则&#…...

做不好PPT的原因
新手制作PPT长犯的10个错误 1.Word搬家 为了节约时间,直接把Word素材复制粘贴到PPT上,没有提炼 2.堆积图表 每个页面上堆积了大量的图表,却没有说明数据反映了什么趋势 3.图表业余 想用图表达自己的逻辑,但没有专业的模板&a…...

嵌入式人工智能(45-基于树莓派4B的扩展板-舵机驱动板PCA9685)
1、简介 智能小车、机械臂、摄像头云台会有多个舵机,而微控制器芯片的PWM输出引脚不够的情况下,就可以用PCA9685(16路舵机)来解决这一问题。 PCA9685是一款I2C总线控制的16通道LED控制器,专为红/绿/蓝/琥珀ÿ…...

【数据结构与算法】建立多个栈的三种方案的优缺点分析
在一个算法中需要建立多个栈时可以选用以下三种方案之一,试问这三方案相比各有什么优缺点? (1)分别用多个顺序存储空间建立多个独立的顺序栈。 (2)多个栈共享一个顺序存储空间。 (3)…...

DjangoRF-14-创建request子应用
注意,本应该是requests模块,为了区分,避免错误,用request 1、进入apps,创建request django-admin startapp request 2、因为只发送请求,没有数据库相关,不需要model。 3、进行序列化 from rest_framework …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...
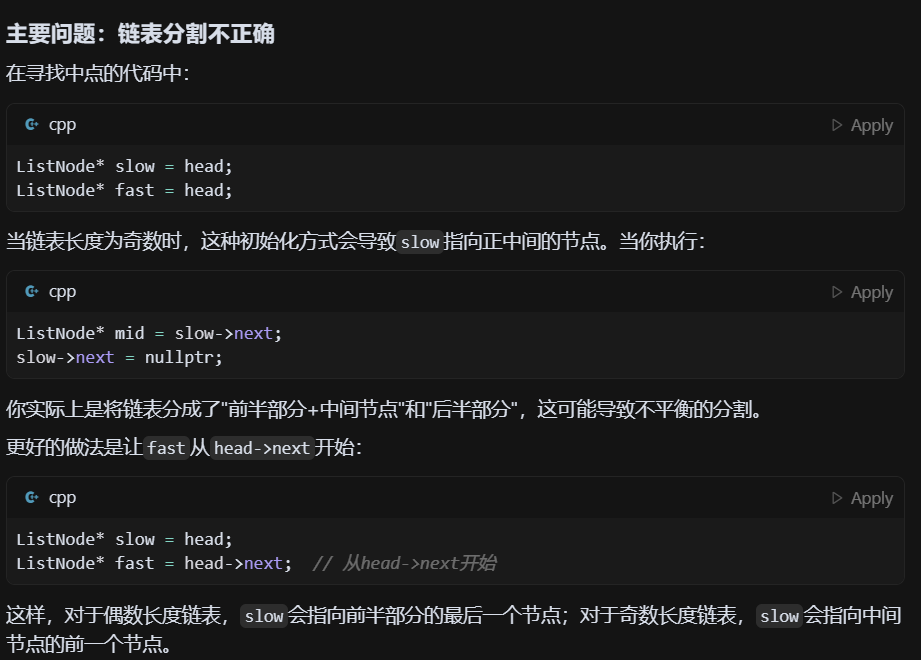
LeetCode - 148. 排序链表
目录 题目 思路 基本情况检查 复杂度分析 执行示例 读者可能出的错误 正确的写法 题目 148. 排序链表 - 力扣(LeetCode) 思路 链表归并排序采用"分治"的策略,主要分为三个步骤: 分割:将链表从中间…...

【docker】Windows安装docker
环境及工具(点击下载) Docker Desktop Installer.exe (windows 环境下运行docker的一款产品) wsl_update_x64 (Linux 内核包) 前期准备 系统要求2: Windows 11:64 位系统&am…...
