Guitar Pro简谱怎么输入 ?如何把简谱设置到六线谱的下面?
一、Guitar Pro简谱怎么输入
简谱在音乐学习、演奏、创作和传播中都起着非常重要的作用,是音乐领域不可或缺的工具。吉他乐谱的制作可以使简谱,也可以使五线谱、六线谱等多种形式,这几种乐谱都可以使用Guitar Pro来完成。下面来看看Guitar Pro简谱怎么输入,如何把简谱设置到六线谱的下面的相关内容。
吉他谱的种类非常丰富,可以使用五线谱、六线谱或者是简谱等。使用Guitar Pro制谱时,这几种乐谱都可以被制作,但当我们使用简谱时,有用户发现新创建的乐谱为空弦-“0”,不知道如何输入新音符,下面看看如何操作。
Guitar Pro 8 win-安装包https://souurl.cn/qHnQS4
Guitar Pro-新闻: https://souurl.cn/yr9xrl
Guitar Pro-首页-网页:https://souurl.cn/EVu5Kn
Guitar Pro-购买-网页:https://souurl.cn/5j8sq2
Guitar Pro-技巧-网页:https://souurl.cn/4Wiidr
Guitar Pro-问题-网页:https://souurl.cn/S9ldiv
Guitar Pro-下载页-网页:https://souurl.cn/krBJYs
Guitar Pro-Guitar Pro 8 mac-安装包:https://souurl.cn/kpMZGm
1.新建音轨
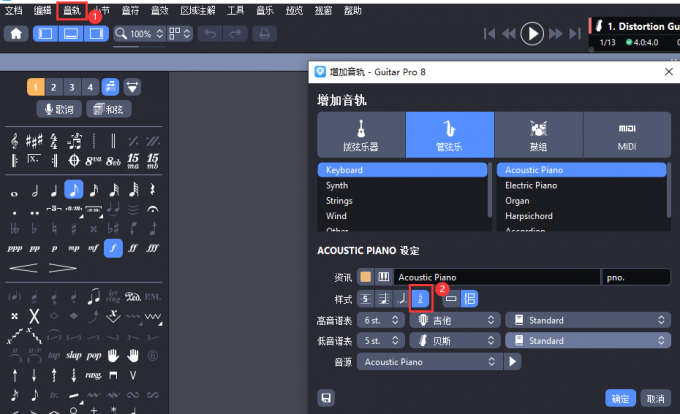
图1:添加音轨
通过展开Guitar Pro顶部菜单栏【音轨】,选择【添加】,打开【增加音轨】编辑界面,在增加音轨编辑界面的【设定-样式】位置选择简谱,单击【确定】,即可打开新音轨界面。
2.输入简谱
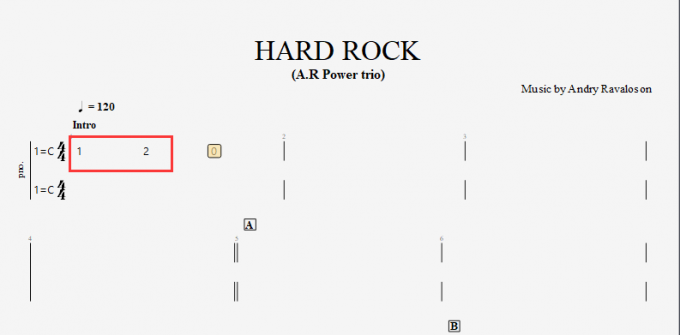
图2:输入简谱
打开简谱后,默认音符为【0】。我们可以直接使用计算机键盘中数字小键盘输入需要的音符,如第一个音符为【1】,直接在计算机键盘中按【1】便能输入,其他音符也按照该种方法输入。
二、如何把简谱设置到六线谱的下面
在Guitar Pro中,将简谱放在六线谱下边需要经过以下几个步骤。
第一步:导入音频文件
图1:导入乐谱
首先,打开Guitar Pro软件,点击界面上的“文件-打开”按钮,选择你想要将简谱放在下面的乐谱文件,将其导入到软件中。
第二步:增加新音轨
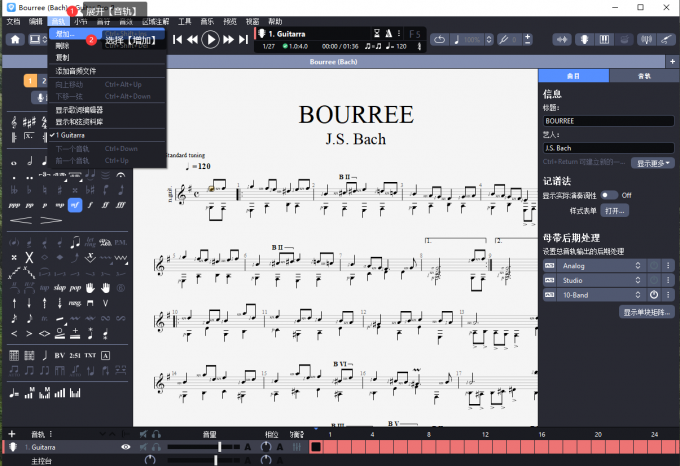
图2:添加音轨
导入音频文件后,点击顶部菜单栏的“音轨”下拉菜单,选择“增加”,打开增加音轨的编辑界面。
第三步:编辑简谱和添加乐器
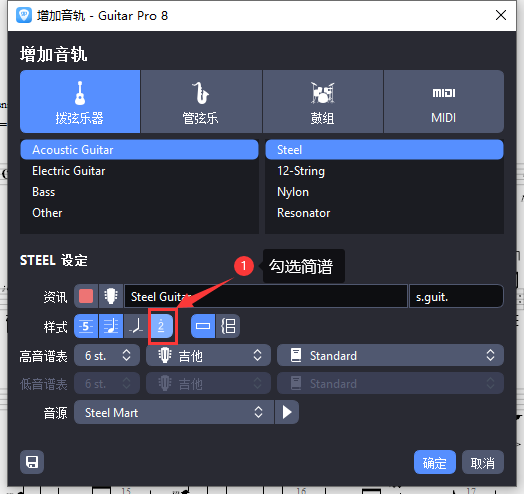
图3:勾选简谱
在新音轨编辑界面内,选择需要的乐器,然后在“样式”位置选择“简谱”,点击“确定”成功添加新音轨。
第四步:使用数字键盘进行简谱编辑
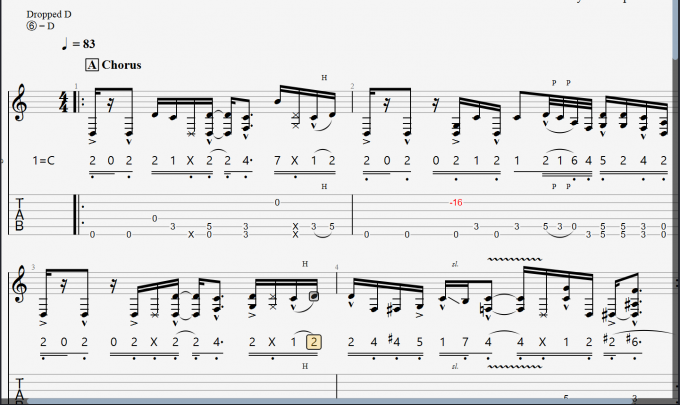
图4:编辑简谱
最后,在乐谱中使用数字键盘进行简谱编辑。在Guitar Pro中,被添加的简谱默认在六线谱下方。通过按下相应的数字键,即可输入相应的音符。您还可以根据需要继续编辑和调整音符,使其符合您的音乐创作。
以上便是Guitar Pro简谱怎么输入,如何把简谱设置到六线谱的下面的相关内容。在Guitar Pro输入简谱非常简单,首先我们需要创建新音轨,然后选择【简谱】模式。在简谱中,默认的音符为【0】,我们可以使用计算机数字键盘进行修改。一起开启你的音乐创作吧!
相关文章:

Guitar Pro简谱怎么输入 ?如何把简谱设置到六线谱的下面?
一、Guitar Pro简谱怎么输入 简谱在音乐学习、演奏、创作和传播中都起着非常重要的作用,是音乐领域不可或缺的工具。吉他乐谱的制作可以使简谱,也可以使五线谱、六线谱等多种形式,这几种乐谱都可以使用Guitar Pro来完成。下面来看看Guitar Pr…...

Python 爬虫项目实战(一):爬取某云热歌榜歌曲
前言 网络爬虫(Web Crawler),也称为网页蜘蛛(Web Spider)或网页机器人(Web Bot),是一种按照既定规则自动浏览网络并提取信息的程序。爬虫的主要用途包括数据采集、网络索引、内容抓…...

Mongodb权限
MongoDB 的权限管理用于确保数据库的安全性并限制用户访问敏感数据。MongoDB 使用基于角色的访问控制(RBAC)来管理权限,允许管理员定义用户和角色,并为这些角色分配相应的权限。 Mongodb的内置角色 数据库角色 角色说明权限read…...

力扣第五十三题——最大子数组和
内容介绍 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 示例 1: 输入:nums [-2,1,-3,4,-1,2,1,-5,4] 输出&…...

达梦数据库:select报错:不是 GROUP BY 表达式
目录 SQL示例报错信息原因排查解决方法一:达梦支持灵活的处理方式,可以直接在查询中加hint参数方法二:修改dm.ini参数GROUP_OPT_FLAG1,动态,会话级参数,不用重启数据库方法三:配置兼容参数&…...

大模型卷向「下半场」,产业场景成拼杀重地
在19世纪的一个雨声潺潺的夏日,诗人拜伦与雪莱在瑞士的湖畔边闲聊,他们聊到了一个大胆的想法:如果能够把一个生物的各个部分制造出来,再组装到一起,赋予它生命的温暖,那会怎样? 这次对话激发了…...

OD C卷 - 多线段数据压缩
多段 线 数据压缩 (200) 如图中每个方格为一个像素(i,j),线的走向只能水平、垂直、倾斜45度;图中线段表示为(2, 8)、(3,7)、(3, 6)、(…...

密码学基础:搞懂Hash函数SHA1、SHA-2、SHA3(2)
目录 1.引入 2. SHA512-224\256 3.SHA-3 4.MD5 5.SM3 1.引入 上篇密码学基础:搞懂Hash函数SHA1、SHA-2、SHA3(1)-CSDN博客,我们先就将基础的SHA1\2讲解了,接下来我们继续聊SHA-3、SHA2变体SHA512_224\256等 2. SHA512-224\256 SHA512…...

C++ 异步编程:std::async、std::future、std::packaged_task 和 std::promise
C 异步编程:std::async、std::future、std::packaged_task 和 std::promise 在现代 C 编程中,异步编程已经成为一种常见的模式。利用 C11 引入的标准库组件 std::async、std::future、std::packaged_task 和 std::promise,我们可以更方便地处…...

OD C卷 - 石头剪刀布游戏
石头剪刀布游戏 (100) 剪刀石头布游戏,A-石头、B-剪刀、C-布游戏规则: 胜负规则,A>B; B>C; C>A;当本场次中有且仅有一种出拳形状优于其他出拳形状,则该形状的玩家是胜利者,否则认为是…...

关于k8s集群中kubectl的陈述式资源管理
1、k8s集群资源管理方式分类 (1)陈述式资源管理方式:增删查比较方便,但是改非常不方便 使用一条kubectl命令和参数选项来实现资源对象管理操作 (2)声明式资源管理方式:yaml文件管理 使用yam…...

XML 学习笔记
简介: (1)XML:可扩展性标记语言,用于传输和存储数据,而不是展示数据,是W3C 推举的数据传输格式。 XML的标签必须自定义,但是在写标签名的时候一定要有含义。 XML 只能有一个根节点…...
MongoDB未授权访问漏洞
2.MongoDB未授权访问漏洞 mongodb数据库是由C编写,主要是为了提供web应可用扩展的一种高性能数据库。开启MongoDB服务时不添加任何参数时,默认是没有权限验证的,登录的用户可以通过默认端口无需密码对数据库任意操作(增、删、改、查高危动作)而且可以远程访问数据库…...
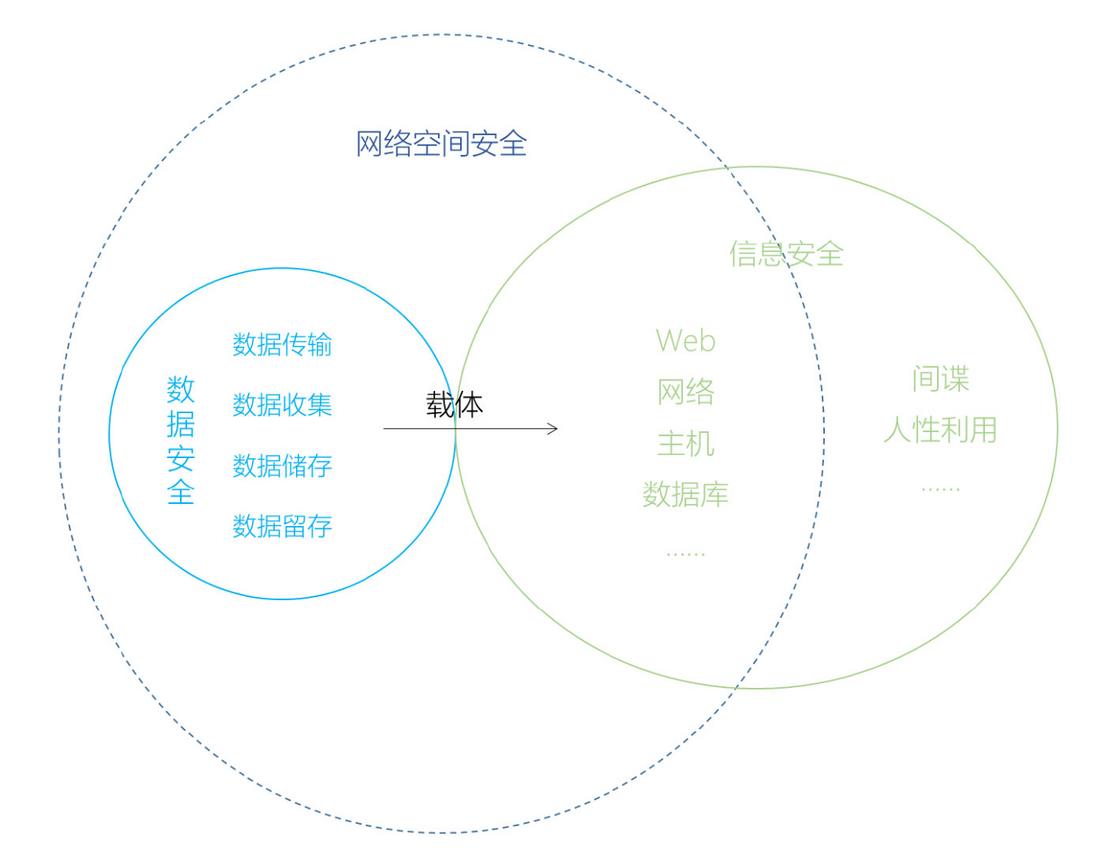
数据安全、信息安全、网络安全区别与联系
关键字: 信息安全 数据安全 网络安全 [导读] 让人更好理解 “数据安全”、“信息安全”、“网络安全” 三者间的区别与联系了,我们汇总了官方机构给这三者的定义,并且网友也给出了自己的看法,一起来看看。 在 “互联网 ” 被广…...

Jenkins未授权访问漏洞 *
漏洞复现 步骤一:使用以下fofa语法进行产品搜索.... port"8080" && app"JENKINS" && title"Dashboard [Jenkins]" 步骤二:在打开的URL中...点击Manage Jenkins --> Scritp Console在执行以下命令..…...

【爬虫原理】
《爬虫》 1、爬虫的概念 概念:(spider,网络蜘蛛)通过互联网上一个个的网络节点,进行数据的提取、整合以及存储 分类: 通用爬虫(了解) 主要用于搜索引擎(百度、…...

计算机组成原理 —— 指令流水线的基本概念
计算机组成原理 —— 指令流水线的基本概念 串行执行(Serial Execution)串行执行的特点串行执行的局限性串行执行的应用场景 并行执行定义基本原理五段式指令流水线优点缺点 流水线的性能指标示例计算 我们来了解一下指令流水线: 首先在这之…...

Python爬虫技术 第31节 持续集成和自动化部署
持续集成和自动化部署 Git版本控制 Git 是一个非常流行的分布式版本控制系统,用于跟踪对项目文件的修改。对于爬虫项目来说,使用Git可以帮助你管理代码的不同版本,协同开发,并且可以在出现问题时回滚到之前的版本。 基本操作&a…...
(第2版)课后习题答案)
数据结构(C语言版)(第2版)课后习题答案
数据结构(C语言版)(第2版)课后习题答案 李冬梅 2015.3 目 录 第 1 章 绪论 1 第 2 章 线性表 5 第 3 章 栈和队列 13 第 4 章 串、数组和广义表 26 第 5 章 树和二叉树 33 第 6 章 图 43 第 7 章 查找 54 第 8 章 排序 65…...
的分析总结及进一步提问)
打开轮盘锁问题(LeetCode)的分析总结及进一步提问
打开轮盘锁问题分析总结,及进一步提问:请给出一组最小步数下的号码序列组合 题目描述 你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。每个拨轮可以自由…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
