选择排序算法改进思路和算法实现
选择排序
在未排序的数组中,用第一个数去和后面的数比较,找出最小的数,和第一个数交换。第一个数已为已排序的数。
相当于0~7
从0~7中找到最小的数放在0
从1~7中找到最小的数放在1
从2~7中找到最小的数放在2
...以此类推
从6~7中找到最小的数放在6
共7次

Java代码如下:
public class SelectSort {public static void main(String[] args) {int[] arr = {5, 3, 8, 6, 2, 7, 1, 4};selectSort(arr);}private static void selectSort(int[] arr){for(int i=0;i<arr.length-1;i++){
// 最小值下标 假设每一轮的第1一个元素是最小值int xb=i;for (int j=i+1;j<arr.length;j++){
// 找到最小元素下标if(arr[j]<arr[xb]){xb=j;}}
// 说明有更小的交换 否则arr[i]就是最小值固定if(xb!=i){int temp=arr[xb];arr[xb]=arr[i];arr[i]=temp;}printArr(arr);}}private static void printArr(int[] arr){for(int i=0;i<arr.length;i++){System.out.print(arr[i]+" ");}System.out.println();}
}
相关文章:

选择排序算法改进思路和算法实现
选择排序 在未排序的数组中,用第一个数去和后面的数比较,找出最小的数,和第一个数交换。第一个数已为已排序的数。 相当于0~7 从0~7中找到最小的数放在0 从1~7中找到最小的数放在1 从2~7中找到最小的数放在2 ...以此类推 从6~7中找到最…...

【文件解析漏洞复现】
一.IIS解析漏洞复现 1.IIS6.X 方式一:目录解析 搭建IIS环境 在网站下建立文件夹的名字为.asp/.asa 的文件夹,其目录内的任何扩展名的文件都被IIS当作asp文件来解析并执行。 访问成功被解析 方式一:目录解析 在IIS 6处理文件解…...

【STL】 vector的底层实现
1.vector的模拟代码完整实现(后面会拆分开一个一个细讲) #pragma once #include<assert.h>// 抓重点namespace bit {/*template<class T>class vector{public:typedef T* iterator;private:T* _a;size_t _size;size_t _capacity;};*/templa…...

责任链模式:解耦职责,优化请求处理
在软件设计中,如何有效地处理复杂的请求是一个重要的课题。 责任链模式(Chain of Responsibility Pattern)提供了一种解耦请求发送者和接收者的方法,使得多个对象都有机会处理请求,从而达到灵活和可扩展的设计。 什么…...

【Scene Transformer】scene transformer论文阅读笔记
文章目录 序言(Abstract)(Introduction)(Related Work)(Methods)(Scene-centric Representation for Agents and Road Graphs)(Encoding Transformer)(Predicting Probabilities for Each Futures)(Joint and Marginal Loss Formulation) (Results)(Discussion)(Questions) sce…...

ESP32在ESP-IDF环境下禁用看门狗
最近使用了一款ESP32的开发板。但在调试时发现出现许多看门狗复位事件: E (8296) task_wdt: Task watchdog got triggered. The following tasks/users did not reset the watchdog in time: E (8296) task_wdt: - IDLE (CPU 0) E (8296) task_wdt: Tasks curre…...

基于 uniapp html5plus API,怎么把图片保存到相册
要将图片保存到相册中,可以使用HTML5 API中的plus.gallery.save方法。以下是一个示例代码,展示如何将图片保存到手机相册: // 图片的URL,可以是本地路径或网络路径 var imageUrl path/to/your/image.jpg;// 调用plus.gallery.sa…...

3.特征工程-特征抽取、特征预处理、特征降维
文章目录 环境配置(必看)头文件引用1.数据集: sklearn代码运行结果 2.字典特征抽取: DictVectorizer代码运行结果稀疏矩阵 3.文本特征抽取(英文文本): CountVectorizer()代码运行结果 4.中文文本分词(中文文本特征抽取使用)代码运行结果 5.中文文本特征抽…...

RISC-V (五)上下文切换和协作式多任务
任务(task) 所谓的任务就是寄存器的当前值。 -smp后面的数字指的是hart的个数,qemu模拟器最大可以有8个核,此文围绕一个核来讲。 QEMU qemu-system-riscv32 QFLAG -nographic -smp 1 -machine virt -bios none 协作式多任务 …...
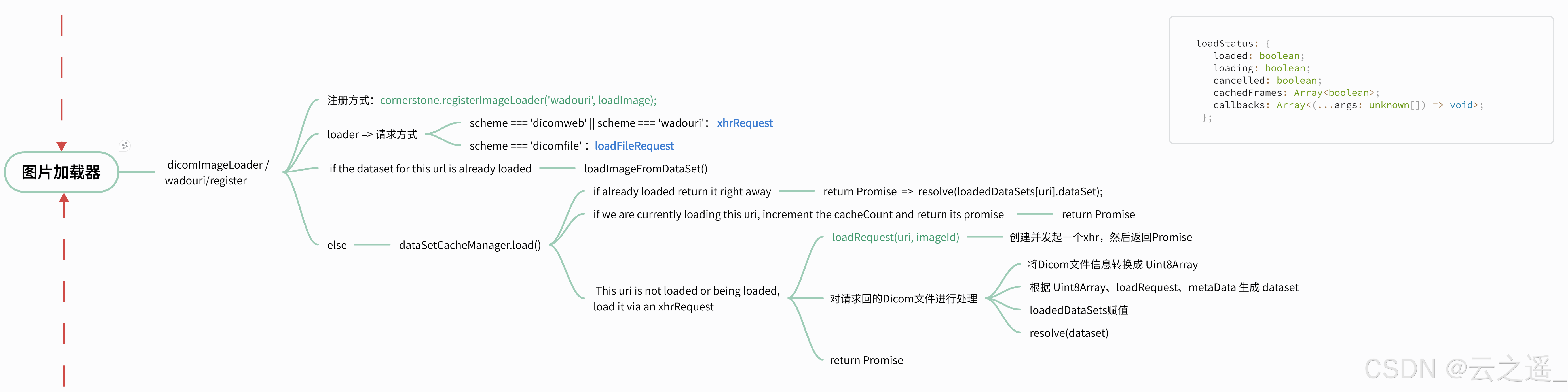
Cornerstone加载本地Dicom文件第二弹 - Blob篇
🍀 引言 当我们刚接触Cornerstone或拿到一组Dicom文件时,如果没有ImageID和后台接口,可能只是想简单测试Cornerstone能否加载这些Dicom文件。在这种情况下,可以使用本地文件加载的方法。之前我们介绍了通过node启动服务器请求文件…...

C语言中整数类型及其类型转换
1.数据的存储和排列 是的,在C语言中,整数类型通常以补码(twos complement)形式存储在内存中。这是因为补码表示法在处理有符号整数的加减运算上更为简便和高效。 2.有符号数和无符号数之间的转换 在C语言中,有符号数和…...

powerjob连接postgresql数据库(支持docker部署)
1.先去pg建一个powerjob-product库 2.首先去拉最新的包,然后找到server模块,把mysql的配置文件信息替换成pg的 spring.datasource.hikari.auto-committrue spring.datasource.remote.hibernate.properties.hibernate.dialecttech.powerjob.server.pers…...
)
浅谈位运算及其应用(c++)
目录 一、位运算的基础(一)位与(&)(二)位或(|)(三)位异或(^)(四)位取反(~)&#x…...

Git版本管理中下列不适于Git的本地工作区域的是
Git版本管理中下列不适于Git的本地工作区域的是 A. 工作目录 B. 代码区 C. 暂存区 D. 资源库 选择B Git本地有四个工作区域: 工作目录(Working Directory)、 暂存区(Stage/Index)、 资源库(Repository或Git Directory)、 git仓库(Remote Di…...

webGL + WebGIS + 数据可视化
webGL: 解释:用于在浏览器中渲染 2D 和 3D 图形。它是基于 OpenGL ES 的,提供了直接操作 GPU 的能力。 库: Three.jsBabylon.jsPixiJSReglGlMatrixOsgjs WebGIS: 解释:用于在 Web 浏览器中处理和展示地…...

职场“老油条”的常规操作,会让你少走许多弯路,尤其这三点
有句话说得好:“在成长的路上,要么受教育,要么受教训。” 挨过打才知道疼,吃过亏才变聪明,从职场“老油条”身上能学到很多经验,不一定全对,但至少有可以借鉴的地方,至少能让你少走…...

Ceres Cuda加速
文章目录 一、简介二、准备工作三、实现代码四、实现效果参考资料一、简介 字Ceres2.2.1版本之后,作者针对于稠密矩阵的分解计算等操作进行了Cuda加速,因此这里就基于此项改动测试一下效果。 二、准备工作 1、首先是需要安装Cuda这个英伟达第三方库,https://developer.nvidi…...

微信小程序生成小程序转发链接,携带参数跳转到另外一个页面
🤵 作者:coderYYY 🧑 个人简介:前端程序媛,目前主攻web前端,后端辅助,其他技术知识也会偶尔分享🍀欢迎和我一起交流!🚀(评论和私信一般会回!!) 👉 个人专栏推荐:《前端项目教程以及代码》 ✨一、前言 需求:在页面A生成分享链接(携带参数),分享到微信…...
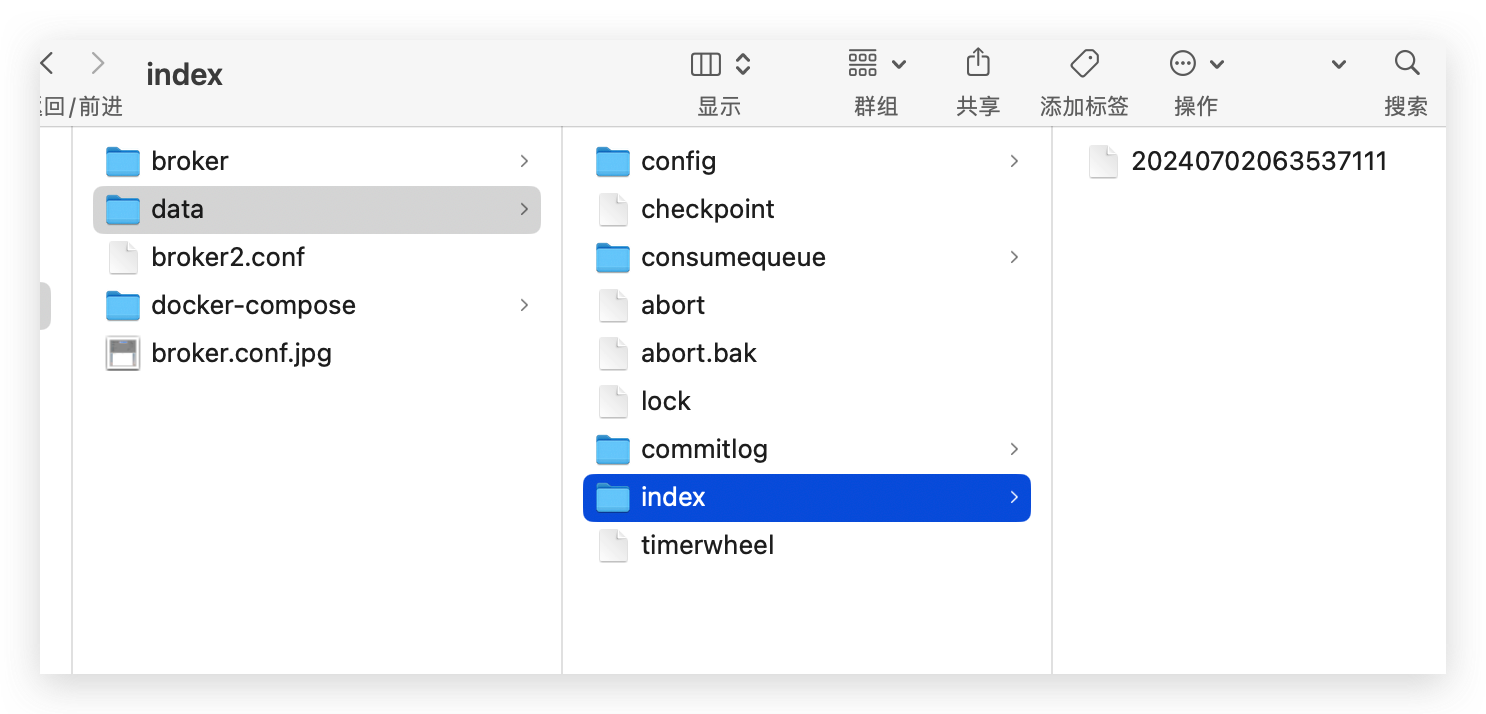
图解RocketMQ之消息如何存储
大家好,我是苍何。 人一辈子最值得炫耀的不应该是你的财富有多少(虽然这话说得有点违心,呵呵),而是你的学习能力。技术更新迭代的速度非常快,那作为程序员,我们就应该拥有一颗拥抱变化的心&…...

2024年中国信创产业发展白皮书精简版
获取方式: 链接:https://pan.baidu.com/s/1rEHMfcCfJm4A40vzrewoCw?pwda5u1 提取码:a5u1 得益于中国数字经济的迅猛发展,2023年中国信创产业规模达20961.9亿元,2027年有望达到37011.3亿元,中国信创市场…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
