avl树自实现(带图),探讨平衡因子与旋转
引子:
在此之前,我们学过了搜索二叉树,这种树,在如果数据有序或接近有序的情况下,二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下,而且普通搜索二叉树无法有重复的元素,对此,我们提出了平衡二叉树,avl树就是比较基础的,一种基于搜索二叉树的改进树,引入了平衡因子与旋转的概念!avl树是由两位俄罗斯的数学家G.M.Adelson-Velskii 和E.M.Landis在1962年 发明了一种方法。
什么是avl树?
AVL树是一种自平衡的二叉搜索树,它的名字来源于它的发明者Adelson-Velsky和Landis。AVL树的特点是任何节点的两个子树的高度(或深度)最大差异为1。这种平衡特性确保了树的查找、插入和删除操作都能在对数时间内完成,即时间复杂度为O(log n)。当向二叉搜索树中插入新结点后,如果能保证每个结点的左右 子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均 搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
1,它的左右子树都是AVL树 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
2,如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(log_2n),搜索时间复杂度O(log_2n)。
avl树的实现
如何实现avl树呢,我们要从图入手,并一步一步实现avl树代码的实现!
我们可以先换一侧树的全部情况,先写出“一半代码”,然后仿照着写就可以了。
一,先试着画出一半的图,思考如何写?以下是一个示范图
图一:

图二:
图三:

二,导入库
#include<iostream>
#include<assert.h>
using namespace std;三,创建节点
//创建节点
template<class K,class V>
class avlTreeNode
{
public:avlTreeNode* _left;//左节点avlTreeNode* _right;//右节点avlTreeNode* _parent;//上级节点int _bf;//平衡因子pair<K, V>_kv;//kv的值;avlTreeNode(const pair<K,V>&kv):_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0),_kv(kv){}
};四,整体框架;
template<class K,class V>
class avlTree
{typedef avlTreeNode<K,V> Node;
public://构造函数avlTree() = default;//拷贝构造函数,树形节点要一个一个拷贝avlTree(const avlTree<K, V>& h){_root = copy(h._root);}//find K值Node* Find( const K& key){Node* cur = _root;while (cur){if (cur->_left->_kv.first < key){cur = cur->_right;}else if (cur->_left->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}//find V值Node* Find(const V& key){Node* cur = _root;while (cur){if (cur->_left->_kv.second < key){cur = cur->_right;}else if (cur->_left->_kv.second > key){cur = cur->_left;}else{return cur;}}return nullptr;}//中序有序,避免了_root是内部private的加密void _InOrder(){_InOrder(_root);cout << endl;}//insertbool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}//要先找到,插入位置Node* parent = nullptr;Node* current = _root;while (current){if (current->_kv.first < kv.first){parent = current;current = current->_right;}else if (current->_kv.first > kv.first){parent = current;current = current->_left;}else{return false;}}//新增节点再链接上去current = new Node(kv);if (kv.first > (parent->_kv.first)){parent->_right = current;}else if (kv.first < (parent->_kv.first)){parent->_left = current;}return true;current->_parent = parent;//更新平衡因子,新节点插入后,AVL树的平衡性可能会遭到破坏,此时就需要更新平衡因子,并检测是否//破坏了AVL树while (current){//左插--,右插++if (current == parent->_left){parent->_bf--;}else if (current == parent->_right){parent->_bf++;}if (parent->_bf == 0){//高度不变,达到最理想状态break;}else if (parent->_bf == -1 || parent->_bf == 1){//向上更新current = parent;parent = parent->_parent;}else if(parent->_bf == 2 || parent->_bf == -2)//不平衡情况{if (parent->_bf == 2 && current->_bf == 1)//左旋RotateL(parent);else if (parent->_bf == -2 && current->_bf == -1)//右旋RotateR(parent);else if (parent->_bf == 2 && current->_bf ==-1)//左右旋RotateRL(parent);else //(parent->_bf == -2 && current->_bf == 1)RotateLR(parent);}elseassert(false);}return true;}//因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不//错与删除不同的时,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。//重载=avlTree<K, V>& operator=(const avlTree<K, V>& h){swap(_root, h._root);return *this;}//析构函数,注意开辟了空间后,对于树形结构的节点要一个一个删除~avlTree(){Destory(_root);_root = nullptr;}int Height(){return _Height(_root);}int Size(){return _Size(_root);}
五,private部分
private://计算有效的节点int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}//计算树的高度,利用递归int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}//对它进行检验bool _IsBalanceTree(Node* root){// 空树也是AVL树if (nullptr == root) return true;//严格检验int TreeHeight_L = _Height(root->_left);int TreeHeight_R = _Height(root->_right);//我们默认的是右到左int diff = TreeHeight_R - TreeHeight_L;//高度与平衡因子的数值不匹配if (diff != root->_bf || (diff > 1 || diff < -1))return false;return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}//中序遍历void _InOrder(Node* root){if (root == nullptr){return;}//左根右;_InOrder(root->_left);cout << root->_kv.first << " :" << root->_kv.second << " ";_InOrder(root->_right);}void RotateL( Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;Node* parent_parent = parent->_parent;if (parent_parent == nullptr){_root = subR;parent_parent = nullptr;}else{if (parent_parent->_left == parent){parent_parent->_left = subR;}else if (parent_parent->_right == parent){parent_parent->_right = subR;}subR->_parent = parent_parent;}subR->_bf = parent->_bf = 0;}void RotateR( Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;Node* parent_parent = parent->_parent;if (parent_parent == nullptr){_root = subL;parent_parent = nullptr;}else{if (parent_parent->_left == parent){parent_parent->_left = subL;}else if (parent_parent->_right == parent){parent_parent->_right = subL;}subL->_parent = parent_parent;}subL->_bf = parent->_bf = 0;}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf =0;}else if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else{assert(false);}}//销毁void Destory(Node* root){if (root==nullptr){return;}Destory(root->_left);Destory(root->_right);Destory(root->_parent);delete root;}//拷贝Node* copy(const Node*& root){if (root == nullptr){return nullptr;}Node* temp = new Node(root->_kv);temp->_left=copy(root->_left);temp->_right=copy(root->_right);temp->_parent=copy(root->_parent);return temp;}Node* _root = nullptr;
};六:说明,对于erase部分先不做处理啦!
七,AVL树的性能 AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这 样可以保证查询时高效的时间复杂度,即log_2 (N)。但是如果要对AVL树做一些结构修改的操 作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时, 有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数 据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
ok,感谢大家的观看,有
问题可以发评论区(微笑!)
相关文章:

avl树自实现(带图),探讨平衡因子与旋转
引子: 在此之前,我们学过了搜索二叉树,这种树,在如果数据有序或接近有序的情况下,二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下,而且普通搜索二叉树无法有…...

Elasticsearch 的DSL查询,聚合查询与多维度数据统计
文章目录 搜索聚合高阶概念 搜索 即从一个索引下按照特定的字段或关键词搜索出符合用户预期的一个或者一堆cocument,然后根据文档的相关度得分,在返回的结果集里并根据得分对这些文档进行一定的排序。 聚合 根据业务需求,对文档中的某个或…...

【如何高效处理前端常见问题:策略与实践】
在快速发展的Web开发领域,前端作为用户与应用程序直接交互的界面,其重要性不言而喻。然而,随着技术的不断演进和项目的复杂化,前端开发者在日常工作中难免会遇到各种挑战和问题。本文旨在深入探讨前端开发中常见的问题类型&#x…...

聊聊前端 JavaScript 的扩展运算符 “...“ 的使用场景
前言 在 JavaScript 中,... 被称为 “扩展运算符” 或 “剩余参数运算符”。 扩展运算符是在 ES6(ECMAScript 2015)中被引入的,目的是为了提高语言的表达能力和代码的可读性。 根据上下文不同,它主要用在数组、对象…...

华为续签了,但我准备离职了
离职华为 今天在牛客网看到一篇帖子,名为《华为续签了,但我准备离职了》。 讲得挺真诚,可能也是一类毕业进华为的同学的心声。 贴主提到,当年自己还是应届毕业的时候,手握多个 offer,最终选的华为ÿ…...

RocketMQ 的认证与授权机制
Apache RocketMQ 是一个高性能、高吞吐量、分布式的消息中间件,广泛应用于异步通信、应用解耦、流量削峰等场景。在企业级应用中,消息安全尤为重要,本文将深入探讨 RocketMQ 的认证与授权机制,帮助开发者和系统管理员更好地理解和…...

【设计模式】六大原则-上
首先什么是设计模式? 相信刚上大学的你和我一样,在学习这门课的时候根本不了解这些设计原则和模式有什么用处,反而不如隔壁的C更有意思,至少还能弹出一个小黑框,给我个hello world。 如何你和我一样也是这么想…...

CRC16循环冗余校验
代码: #include<stdio.h> #include <stdint.h>#define uchar unsigned char #define uint unsigned int static const uint8_t auchCRCHi[] { 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x0…...

Mysql80主从复制搭建;遇到问题 Slave_IO_Running: Connecting和Slave_SQL_Running以及解决过程
总结主要步骤 1.配置一个提供复制的账号; 创建用户 CREATE USER replication% IDENTIFIED BY your_password; GRANT REPLICATION SLAVE ON *.* TO replication%; FLUSH PRIVILEGES;2.修改配置 选择模式 主库配置; windows的得话是my.ini文件 默认这个目…...

Yarn网络代理配置指南:在受限网络环境中优化依赖管理
Yarn是一个现代的包管理器,用于JavaScript项目,它提供了快速、可靠和安全的依赖管理方式。然而,在某些受限的网络环境中,例如公司内网或某些国家地区,直接连接到公共npm仓库可能不可行或效率低下。这时,配置…...

AOE网及其求解关键路径
全称 Activity on Edge Network 边活动网 特点 仅存在 有向无环图 作用 用于记录完成整个工程至少花费的时间 > 哪条路径最耗时?也就是“ 关键路径 ” AOE网元素介绍 关键活动 关键路径上的活动称为关键活动 , 关键活动是不允许拖延的&#x…...

【FPGA】modelsim编译verilog代码产生错误集合
错误1: LHS in procedural continuous assignment may not be a net 可能是一些变量不能放在一些begin和end中,改下assign的位置 新手求助 LHS in procedural continuous assignment may not be a net - 数字IC设计讨论(IC前端|FPGA|ASIC) - EETOP 创…...
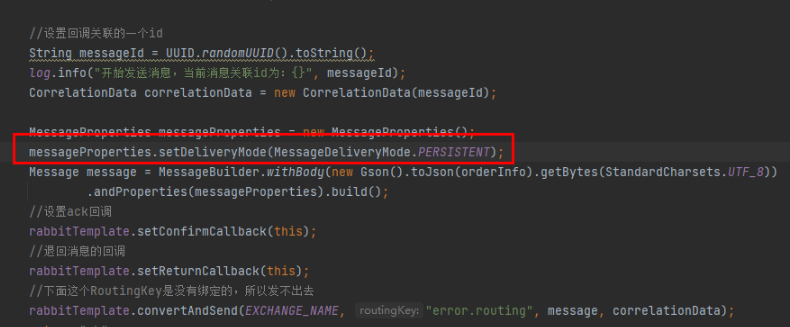
Rabbitmq的持久化机制
我们通过手动应答处理了在消费者出故障消息丢失的情况,但是如何保障当 RabbitMQ 服务停掉以后消息生产者发送过来的消息不丢失。默认情况下 RabbitMQ 退出或由于某种原因崩溃时,它会清空队列和消息,除非告知它不要这样做。确保消息不会丢失可…...

Unity UnityWebRequest封装类
简化api调用流程,非常奈斯。 RestWebClient.cs using System; using System.Collections; using UnityEngine; using UnityEngine.Networking;namespace MYTOOL.RestClient {/// <summary>/// UnityWebRequest封装类/// </summary>public class RestW…...

JVM内存划分
Java虚拟机(JVM)的内存划分是指JVM在运行时所使用的内存区域的组织和管理方式。JVM内存主要分为以下几个区域: 堆区(Heap): 用途:用于存储所有对象实例和数组,是JVM中最大的一块内存…...

c++ 全排列
在C中,全排列(permutation)可以使用递归算法或标准库函数来实现。以下是使用递归和STL库std::next_permutation来生成一个集合的全排列的两种方法。 方法一:递归算法 递归方法通过交换元素来生成所有可能的排列组合。 #include…...
未授权访问漏洞系列详解⑤!
Kubernetes Api Server未授权访问漏洞 Kubernetes 的服务在正常启动后会开启两个端口:Localhost Port(默认8080)Secure Port(默认6443)。这两个端口都是提供 Api Server 服务的,一个可以直接通过Web 访问,另一个可以通过 kubectl 客户端进行调用。如果运…...

【CONDA】库冲突解决办法
如今,使用PYTHON作为开发语言时,或多或少都会使用到conda。安装Annaconda时一般都会选择在启动终端时进入conda的base环境。该操作,实际上是在~/.bashrc中添加如下脚本: # >>> conda initialize >>> # !! Cont…...

【网络世界】数据链路层
目录 🌈前言🌈 📁 初识数据链路层 📂 概念 📂 协议格式 📁 MAC地址 📂 概念 📂 与IP地址的区别 📁 MTU 📂 对IP协议的影响 📂 对UDP协议的影响…...

AllReduce通信库;Reduce+LayerNorm+Broadcast 算子;LayerNorm(层归一化)和Broadcast(广播)操作;
目录 AllReduce通信库 一、定义与作用 二、常见AllReduce通信库 三、AllReduce通信算法 四、总结 Reduce+LayerNorm+Broadcast 算子 1. Reduce 算子 2. LayerNorm 算子 3. Broadcast 算子 组合作用 LayerNorm(层归一化)和Broadcast(广播)操作 提出的创新方案解析 优点与潜在…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

