动态规划.
目录
(一)递归到动规的一般转化方法
(二)动规解题的一般思路
1. 将原问题分解为子问题
2. 确定状态
3. 确定一些初始状态(边界状态)的值
4. 确定状态转移方程
(三)能用动规解决的问题的特点
1.最优子结构
2.无后效性
(四)动归的常用两种形式
1)递归型
2)递推型
(五)例题
数字三角形
题目
解题思路
题目解答
运行该程序会超时,为什么呢?
递归改递推
空间优化
最长上升子序列
题目
解题思路
1.找子问题
2. 确定状态
3. 找出状态转移方程
题目解答
公共子序列
题目
解题思路
题目解答
(一)递归到动规的一般转化方法
递归函数有n个参数,就定义一个n维的数组,数组的下标是递归函数参数的取值范围,数组元素的值是递归函数的返回值,这样就可以从边界值开始,逐步填充数组,相当于计算递归函数值的逆过程。
(二)动规解题的一般思路
1. 将原问题分解为子问题
把原问题分解为若干个子问题,子问题和原问题形式相同或类似,只不过规模变小了。子问题都解决,原问题即解决(数字三角形例)。
子问题的解一旦求出就会被保存,所以每个子问题只需求解一次。
2. 确定状态
在用动态规划解题时,我们往往将和子问题相关的各个变量的一组取值,称之为一个“状态”。一个“状态”对应于一个或多个子问题,所谓某个“状态”下的“值”,就是这个“状态”所对应的子问题的解。
用动态规划解题,经常碰到的情况是,K个整型变量能构成一个状态(如数字三角形中的行号和列号这两个变量构成“状态”)。如果这K个整型变量的取值范围分别是N1, N2, ……Nk,那么,我们就可以用一个K维的数组array[N1] [N2]……[Nk]来存储各个状态的“值”。这个“值”未必就是一个整数或浮点数,可能是需要一个结构才能表示的,那么array就可以是一个结构数组。一个 “状态”下的“值”通常会是一个或多个子问题的解。
3. 确定一些初始状态(边界状态)的值
以“数字三角形”为例,初始状态就是底边数字,值就是底边数字值。
4. 确定状态转移方程
定义出什么是“状态”,以及在该 “状态”下的“值”后,就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的 “状态”,求出另一个“状态”的“值”(“人人为我”递推型)。状态的迁移可以用递推公式表示,此递推公式也可被称作“状态转移方程”。
(三)能用动规解决的问题的特点
1.最优子结构
问题具有最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质。
2.无后效性
无后效性。当前的若干个状态值一旦确定,则此后过程的演变就只和这若干个状态的值有关,和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态,没有关系。
(四)动归的常用两种形式
1)递归型
优点:直观,容易编写
缺点:可能会因递归层数太深导致爆栈,函数调用带来额外时间开销。无法使用滚动数组节省空间。总体来说,比递推型慢。
2)递推型
效率高,有可能使用滚动数组节省空间
(五)例题
数字三角形

题目
图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,你的任务就是找到最大的和。
注意:路径上的每一步只能从一个数走到下一层上和它最近的左边的那个数或者右边的那个数。
输入
输入的是一行是一个整数N (1 < N <= 100),给出三角形的行数。下面的N行给出数字三角形。数字三角形上的数的范围都在0和100之间。
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5输出
输出最大的和。
30解题思路
用二维数组存放数字三角形。
D( r, j) : 第r行第 j 个数字(r,j从1开始算)
MaxSum(r, j) : 从D(r,j)到底边的各条路径中,
最佳路径的数字之和。
问题:求 MaxSum(1,1)
典型的递归问题。
D(r, j)出发,下一步只能走D(r+1,j)或者D(r+1, j+1)。故对于N行的三角形:
if ( r == N)
MaxSum(r,j) = D(r,j)
else
MaxSum( r, j) = Max{ MaxSum(r+1,j), MaxSum(r+1,j+1) }+ D(r,j)
题目解答
#include <iostream>
#include <algorithm>
#define MAX 101
using namespace std;
int D[MAX][MAX];
int n;
int MaxSum(int i, int j){if(i==n)return D[i][j]; int x = MaxSum(i+1,j); int y = MaxSum(i+1,j+1); return max(x,y)+D[i][j];
}
int main(){int i,j;cin >> n;for(i=1;i<=n;i++)for(j=1;j<=i;j++)cin >> D[i][j];cout << MaxSum(1,1) << endl;
}运行该程序会超时,为什么呢?

原因是重复计算,如果采用递规的方法,深度遍历每条路径,存在大量重复计算。则时间复杂度为 2n,对于 n = 100 行,肯定超时。
改进
如果每算出一个MaxSum(r,j)就保存起来,下次用到其值的时候直接取用,则可免去重复计算。那么可以用O(n2)时间完成计算。因为三角形的数字总数是 n(n+1)/2
#include <iostream>
#include <algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int n;
int maxSum[MAX][MAX];
int MaxSum(int i, int j)
{if( maxSum[i][j] != -1 )return maxSum[i][j]; if(i==n) maxSum[i][j] = D[i][j]; else {int x = MaxSum(i+1,j); int y = MaxSum(i+1,j+1); maxSum[i][j] = max(x,y)+ D[i][j];}return maxSum[i][j];int main(){int i,j; cin >> n; for(i=1;i<=n;i++)for(j=1;j<=i;j++) {cin >> D[i][j]; maxSum[i][j] = -1;}cout << MaxSum(1,1) << endl;
}
递归改递推
#include <iostream>
#include <algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int n;
int maxSum[MAX][MAX]; int main(){ int i,j; cin >> n; for(i=1;i<=n;i++) for(j=1;j<=i;j++) cin >> D[i][j];for( int i = 1;i <= n; ++ i )maxSum[n][i] = D[n][i];for( int i = n-1; i>= 1; --i ) for( int j = 1; j <= i; ++j ) maxSum[i][j] =max(maxSum[i+1][j],maxSum[i+1][j+1]) + D[i][j];cout << maxSum[1][1] << endl;
}空间优化
没必要用二维maxSum数组存储每一个MaxSum(r,j),只要从底层一行行向上递推,那么只要一维数组maxSum[100]即可,即只要存储一行的MaxSum值就可以。
进一步考虑,连maxSum数组都可以不要,直接用D的第n行替代maxSum即可。
节省空间,时间复杂度不变
#include <iostream>
#include <algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int n;
int * maxSum; int main(){ int i,j; cin >> n; for(i=1;i<=n;i++) for(j=1;j<=i;j++) cin >> D[i][j]; maxSum = D[n]; //maxSum指向第n行for( int i = n-1; i>= 1; --i ) for( int j = 1; j <= i; ++j ) maxSum[j] = max(maxSum[j],maxSum[j+1]) + D[i][j]; cout << maxSum[1] << endl;
}最长上升子序列

题目
一个数的序列bi,当b1 < b2 < ... < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, ..., aN),我们可以得到一些上升的子序列(ai1, ai2, ..., aiK),这里1 <= i1 < i2 < ... < iK <= N。比如,对于序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4,比如子序列(1, 3, 5, 8).
你的任务,就是对于给定的序列,求出最长上升子序列的长度。
输入
输入的第一行是序列的长度N (1 <= N <= 1000)。第二行给出序列中的N个整数,这些整数的取值范围都在0到10000。
7
1 7 3 5 9 4 8输出
最长上升子序列的长度。
4解题思路
1.找子问题
“求序列的前n个元素的最长上升子序列的长度”是个子问题,但这样分解子问题,不具有“无后效性”
假设F(n) = x,但可能有多个序列满足F(n) = x。有的序列的最后一个元素比 an+1小,则加上an+1就能形成更长上升子序列;有的序列最后一个元素不比an+1小……以后的事情受如何达到状态n的影响,不符合“无后效性”
“求以ak(k=1, 2, 3…N)为终点的最长上升子序列的长度”
一个上升子序列中最右边的那个数,称为该子序列的 “终点”。
虽然这个子问题和原问题形式上并不完全一样,但是只要这N个子问题都解决了,那么这N个子问题的解中,最大的那个就是整个问题的解。2. 确定状态
子问题只和一个变量-- 数字的位置相关。因此序列中数的位置k 就是“状态”,而状态 k 对应的“值”,就是以ak做为 “终点”的最长上升子序列的长度。
状态一共有N个。3. 找出状态转移方程
maxLen (k)表示以ak做为“终点”的最长上升子序列的长度那么:
初始状态:maxLen (1) = 1
maxLen (k) = max { maxLen (i):1<=i < k 且 ai < ak且 k≠1 } + 1
若找不到这样的i,则maxLen(k) = 1
maxLen(k)的值,就是在ak左边,“终点”数值小于ak ,且长度最大的那个上升子序列的长度再加1。因为ak左边任何“终点”小于ak的子序列,加上ak后就能形成一个更长的上升子序列。
题目解答
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 1010;
int a[MAXN];
int maxLen[MAXN];int main(){int N;cin >> N;for(int i = 1;i <= N;++i){cin >>a[i];maxLen[i] = 1;}for(int i = 2;i <= N;++i){//每次求以第i个数为终点的最长上升子序列的长度for( int j = 1; j < i; ++j) //察看以第j个数为终点的最长上升子序列if( a[i] > a[j] )maxLen[i] = max(maxLen[i],maxLen[j]+1); }cout << * max_element(maxLen+1,maxLen + N + 1 );return 0;
}} //时间复杂度O(N2)公共子序列

题目
我们称序列Z = < z1, z2, ..., zk >是序列X = < x1, x2, ..., xm >的子序列当且仅当存在 严格上升 的序列< i1, i2, ..., ik >,使得对j = 1, 2, ... ,k, 有xij = zj。比如Z = < a, b, f, c > 是X = < a, b, c, f, b, c >的子序列。
现在给出两个序列X和Y,你的任务是找到X和Y的最大公共子序列,也就是说要找到一个最长的序列Z,使得Z既是X的子序列也是Y的子序列。
输入
输入包括多组测试数据。每组数据包括一行,给出两个长度不超过200的字符串,表示两个序列。两个字符串之间由若干个空格隔开。
abcfbc abfcab
programming contest
abcd mnp输出
对每组输入数据,输出一行,给出两个序列的最大公共子序列的长度。
4
2
0解题思路
输入两个串s1,s2,设MaxLen(i,j)表示:
s1的左边i个字符形成的子串,与s2左边的j个字符形成的子串的最长公共子序列的长度(i,j从0开始算)
MaxLen(i,j) 就是本题的“状态”
假定 len1 = strlen(s1),len2 = strlen(s2)
那么题目就是要求 MaxLen(len1,len2)
显然:
MaxLen(n,0) = 0 ( n= 0…len1)
MaxLen(0,n) = 0 ( n=0…len2)
递推公式:
if ( s1[i-1] == s2[j-1] ) //s1的最左边字符是s1[0]
MaxLen(i,j) = MaxLen(i-1,j-1) + 1;
else
MaxLen(i,j) = Max(MaxLen(i,j-1),MaxLen(i-1,j) );
时间复杂度O(mn) m,n是两个字串长度

S1[i-1]!= s2[j-1]时,MaxLen(S1,S2)不会比MaxLen(S1,S2j-1) 和MaxLen(S1i-1,S2)两者之中任何一个小,也不会比两者都大。
题目解答
#include <iostream>
#include <cstring>
using namespace std;
char sz1[1000];
char sz2[1000];
int maxLen[1000][1000];int main(){while( cin >> sz1 >> sz2 ){int length1 = strlen(sz1);int length2 = strlen(sz2);int nTmp;int i,j;for(i = 0;i <= length1;i++)maxLen[i][0] = 0;for(j = 0;j <= length2;j++)maxLen[0][j] = 0;for(i = 1;i <= length1;i++){for(j = 1; j <= length2;j++){if(sz1[i-1] == sz2[j-1])maxLen[i][j] = maxLen[i-1][j-1] + 1;elsemaxLen[i][j] = max(maxLen[i][j-1],maxLen[i-1][j]); }}cout << maxLen[length1][length2] << endl;}return 0;
}相关文章:

动态规划.
目录 (一)递归到动规的一般转化方法 (二)动规解题的一般思路 1. 将原问题分解为子问题 2. 确定状态 3. 确定一些初始状态(边界状态)的值 4. 确定状态转移方程 (三)能用动规解…...

PHP常用函数
字符串 strlen()获取字符串长度strpos()在字符串内查找一个字符或一段指定的文本,返回第一次出现的位置或falsestripos()同上,但不区分大小写strrpos()同上上,返回最后一…...

完全用python 实现消息中间件4
为了进一步完善这个消息中间件,我们可以添加以下功能: 消息确认:客户端可以发送一个确认消息,表明消息已经被正确接收。消息队列:使用一个队列来存储消息,而不是直接存储在字典中。多消费者支持࿱…...

公司新来的两个Java后端,因题背太熟轻松过面试?
以前面试是背八股文,而2024年的后端面试都是流行问场景题!建议大家把面试想简单一点,顺的场景题直接给有需要的人,希望能对大家有所帮助! 由于平台篇幅原因,很多java面试资料内容展示不了,需要…...

Pinia状态管理库
为了跨组件传递JWT令牌,我们就会利用Pinia状态管理库,它允许跨组件或页面共享状态。 使用Pinia步骤: 安装pinia:cnpm install pinia 在vue应用实例中使用pinia 在src/stores/token.js中定义store 在组件中使用store 1.在main.js文…...

利用ffmpeg转码视频为gif图片,调整gif图片的大小
【1】压缩gif图片大小 一般发布技术文章的时候经常要插入GIF图演示软件效果,但是一些编辑器总是限制大小,但是录制的时候可能一不小心就搞大了。 要将 GIF 图片大小限制在 10MB 内,可以使用 FFmpeg 进行压缩。 以下是一个ffmpeg的命令&…...

【Java 第四篇章】流程控制、容器
一、流程控制 1、概念 //1.if//2.if...else//3.if...else if...else...//4.switch//5.跳出循环体:break和continue2、语法 //1. ifif(条件表达式){//执行代码块}//2.if...elseif(条件表达式){//条件表达式为真执行的代码块} else {//条件表达式为假执行的代码块}//…...
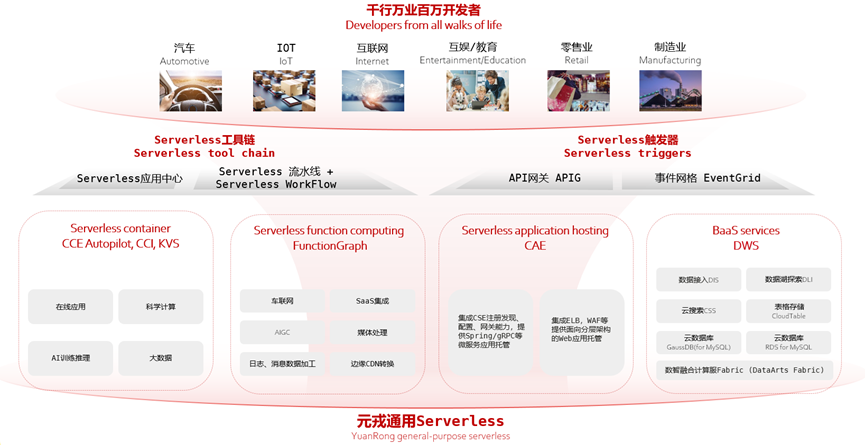
华为云全域Serverless技术创新:全球首创通用Serverless平台被ACM SIGCOMM录用
华为开发者大会2024(HDC 2024)在东莞松山湖圆满结束,期间华为云主办的“全域Serverless时代:技术创新引领,赋能行业实践”专题论坛,向广大开发者传递了Serverless领域的前沿思考和实践,现场座无…...

除自身以外数组的相乘 C++
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂…...

Element UI 如何配置文件来设置全局的语言选项。
Element UI 允许你通过配置文件来设置全局的语言选项,这样你可以方便地切换组件的语言。以下是如何配置 Element UI 以设置全局语言选项的步骤: 1. 安装 Element UI 确保你已经安装了 Element UI。 npm install element-ui --save2. 引入语言包 Elem…...

Windows 常用命令集锦
目录 一、文件和目录管理 1.1 文件操作 1.2 目录操作 二、系统信息 2.1 基本系统信息 2.2 硬件信息 三、网络管理 3.1 基本网络命令 3.2 网络诊断 四、进程管理 4.1 查看进程 4.2 管理进程 五、磁盘管理 5.1 磁盘操作 5.2 磁盘分区 六、IIS操作 通过上述命令&am…...

第一阶段面试问题(后半部分)
1. c语言中const *p的用法 (1)const int *p; 或 int const *p; 指向常量整数的指针,通过这个指针不能修改它所指向的整数值,但可以修改指针本身来指向其他地址 const int a 10; const int *p &a; // *p 20; // 错误&…...

【AIGC】ComfyUI入门-使用ComfyUI_MagicClothing插件在生成图片时候出现的问题
最近想自己实现自动换装的工作流,在使用ComfyUI_MagicClothing插件的时候,出现了一个奇怪的问题。这个问题不是插件的问题,是环境配置问题。 问题内容如下: Exception during processing!!! D:\a_work\1\s\onnxruntime\python\onnxruntime_pybind_state.cc:891 onnxrunti…...

巴黎奥运会8K转播科技为国产品牌自主研发设计
这个夏天,顶流是属于巴黎奥运会中国队的。 20枚金牌、15枚银牌、12枚铜牌......这个数字正随着赛事推进而不停在增加。赛场之上,中国健儿奋力拼搏、捷报频传,令人热血沸腾;赛场之外,另一支来自中国企业的“奥运选手”…...

【Material-UI】Button 组件中的图标和标签按钮(Buttons with Icons and Label)详解
文章目录 一、基础用法1. 左侧图标(startIcon)2. 右侧图标(endIcon) 二、图标与标签的搭配三、高级用法和最佳实践1. 自定义图标2. 视觉一致性3. 动态图标 四、总结 在现代用户界面设计中,图标在提高用户体验ÿ…...
K个一组翻转链表(LeetCode)
题目 给你链表的头节点 ,每 个节点一组进行翻转,请你返回修改后的链表。 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 的整数倍,那么请将最后剩余的节点保持原有顺序。 你不能只是单纯的改变节点内部的值&…...

2-56 基于matlab的图像融合增强技术
基于matlab的图像融合增强技术。通过原始图像——傅里叶变换——频率域滤波处理——傅里叶变换——增强后的图像。傅立叶变换以及傅立叶反变换.过程就是将空间的信息分解为在频率上的表示,通过傅立叶正反变换的处理,才使得频率域上的处理可以用于图像的增强。程序已调通&#x…...

序列化定义以及使用和注意事项
什么是序列化和反序列化 序列化:是将对象转换为可传输或存储的过程, 反序列化:通常是将字节流或是其他数据格式或源数据转为对象的过程。 序列化的作用 对象的持久化:将对象的状态保存到磁盘或数据库中,以便在程序…...

吴恩达机器学习COURSE1 WEEK3
COURSE1 WEEK3 逻辑回归 逻辑回归主要用于分类任务 只有两种输出结果的分类任务叫做二元分类,例如预测垃圾邮件,只能回答是或否 实际上,在逻辑回归中,我们要做的任务就类似于在数据集中画出一个这样的曲线,用来作为…...

白骑士的PyCharm教学高级篇 3.1 性能分析与优化
系列目录 上一篇:白骑士的PyCharm教学进阶篇 2.5 数据库连接与管理 在软件开发中,性能分析与优化是提高程序运行效率和用户体验的重要环节。PyCharm提供了强大的性能分析工具,帮助你识别和优化代码中的性能瓶颈。本文将详细介绍PyCharm中的代…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
