机器学习 第10章-降维与度量学习
机器学习 第10章-降维与度量学习
10.1 k近邻学习
k近邻(k-Nearest Neighbor,简称kNN)学习是一种常用的监督学习方法其工作机制非常简单:给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个“邻居”的信息来进行预测。通常,在分类任务中可使用“投票法”,即选择这k个样本中出现最多的类别标记作为预测结果;在回归任务中可使用“平均法”,即将这k个样本的实值输出标记的平均值作为预测结果;还可基于距离远近进行加权平均或加权投票,距离越近的样本权重越大。
与前面介绍的学习方法相比,k近邻学习有一个明显的不同之处:它似乎没有显式的训练过程!事实上,它是“懒惰学习”(lazy learning)的著名代表此类学习技术在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理;相应的,那些在训练阶段就对样本进行学习处理的方法,称为“急切学习”(eager learning)。
图10.1给出了k近邻分类器的一个示意图。显然,k是一个重要参数,当k取不同值时,分类结果会有显著不同。另一方面,若采用不同的距离计算方式,则找出的“近邻”可能有显著差别,从而也会导致分类结果有显著不同。

10.2 低维嵌入
事实上,在高维情形下出现的数据样本稀疏、距离计算困难等问题是所有机器学习方法共同面临的严重障碍,被称为“维数灾难”(curse of dimensionality)。
缓解维数灾难的一个重要途径是降维(dimensionreduction),亦称“维数约简”,即通过某种数学变换将原始高维属性空间转变为一个低维“子空间”(subspace),在这个子空间中样本密度大幅提高,距离计算也变得更为容易。为什么能进行降维?这是因为在很多时候,人们观测或收集到的数据样本虽是高维的,但与学习任务密切相关的也许仅是某个低维分布,即高维空间中的一个低维“嵌入”(embedding)。图10.2给出了一个直观的例子。原始高维空间中的样本点,在这个低维嵌入子空间中更容易进行学习。

假定 m m m个样本在原始空间的距离矩阵为 D ∈ R m ∗ m D\in R^{m*m} D∈Rm∗m,其中第 i i i行 j j j列的元素 d i s t i j dist_{ij} distij为样本 x i x_i xi到 x j x_j xj的距离,目标是要获取样本在 d ′ {d}' d′维空间的表示 Z ∈ R d ′ ∗ m , d ′ ≤ d Z\in R^{{d}'*m},{d}'\leq d Z∈Rd′∗m,d′≤d,且任意两个样本在 d ′ {d}' d′维空间中的欧氏距离等于原始空间中的距离,即 ∥ z i − z j ∥ = d i s t i j \left \| z_i-z_j \right \|=dist_{ij} ∥zi−zj∥=distij。
令 B = Z T Z ∈ R m ∗ m B=Z^T Z\in R^{m*m} B=ZTZ∈Rm∗m,其中 B B B为降维后样本的内积矩阵 b i j = z i T z j b_{ij}=z_i^Tz_j bij=ziTzj,则有:
d i s t i j 2 = ∣ ∣ z i ∣ ∣ 2 + ∣ ∣ z j ∣ ∣ 2 − 2 z i T z j = b i i + b j j − 2 b i j dist_{ij}^2=||z_i||^2+||z_j||^2-2z_i^Tz_j=b_{ii}+b_{jj}-2b_{ij} distij2=∣∣zi∣∣2+∣∣zj∣∣2−2ziTzj=bii+bjj−2bij
令降维后的样本 Z Z Z中心化,即 ∑ i = 1 m z i = 0 ∑^m_{i=1}z_i=0 ∑i=1mzi=0,且矩阵B的行列之和都为0,可以得到:
∑ i = 1 m d i s t i j 2 = t r ( B ) + m b j j \sum_{i=1}^{m}dist_{ij}^2=tr(B)+mb_{jj} i=1∑mdistij2=tr(B)+mbjj
∑ j = 1 m d i s t i j 2 = t r ( B ) + m b i i \sum_{j=1}^{m}dist_{ij}^2=tr(B)+mb_{ii} j=1∑mdistij2=tr(B)+mbii
∑ i = 1 m ∑ i = j m d i s t i j 2 = 2 m t r ( B ) \sum_{i=1}^{m}\sum_{i=j}^{m}dist_{ij}^2=2m\: tr(B) i=1∑mi=j∑mdistij2=2mtr(B)
联立得:
b i j = − 1 2 ( d i s t i j 2 − d i s t i ⋅ 2 − d i s t ⋅ j 2 + d i s t ⋅ ⋅ 2 ) b_{ij}=-\frac{1}{2}(dist_{ij}^2-dist_{i\cdot }^2-dist_{\cdot j}^2+dist_{\cdot \cdot }^2) bij=−21(distij2−disti⋅2−dist⋅j2+dist⋅⋅2)
整个算法描述如下图所示:

基于线性变换来进行降维的方法称为线性降维方法,和MDS方法不同之处是对低维子空间的性质有不同的要求。
10.3 主成分分析
主成分分析(Principal Component Analysis,简称 PCA)是最常用的一种降维方法。
对于正交属性空间中的样本点,如何用一个超平面(直线的高维推广)对所有样本进行恰当的表达?
容易想到,若存在这样的超平面,那么它大概应具有这样的性质:
最近重构性:样本点到这个超平面的距离都足够近;
最大可分性:样本点在这个超平面上的投影能尽可能分开
根据最近重构性,可以得到:
KaTeX parse error: Undefined control sequence: \; at position 20: …derset{W}{min} \̲;̲ \; -tr(W^TXX^T…
根据最大可分性,可以得到:
KaTeX parse error: Undefined control sequence: \; at position 19: …nderset{W}{max}\̲;̲ \; \; tr(W^TXX…
显然两式等价,对其使用拉格朗日乘子法可得:
X X T W = λ W XX^TW=\lambda W XXTW=λW
于是,只需对协方差矩阵 X X T XX^T XXT进行特征值分解,将求得的特征值排序: λ 1 ≥ λ 2 ≥ 。。。 ≥ λ d λ_1≥λ_2≥。。。≥λ_d λ1≥λ2≥。。。≥λd,再取前 d ′ d' d′个特征值对应的特征向量构成 W = ( w 1 , w 2 , . . . , w d ′ ) W=(w_1,w_2,...,w_{d'}) W=(w1,w2,...,wd′)。这就是主成分分析的解。
PCA 算法描述如图 10.5 所示。

PCA 仅需保留W与样本的均值向量即可通过简单的向量减法和矩阵-向量乘法将新样本投影至低维空间中。显然,低维空间与原始高维空间必有不同因为对应于最小的d-d个特征值的特征向量被舍弃了,这是降维导致的结果但舍弃这部分信息往往是必要的:一方面,舍弃这部分信息之后能使样本的采样密度增大,这正是降维的重要动机;另一方面,当数据受到噪声影响时,最小的特征值所对应的特征向量往往与噪声有关,将它们舍弃能在一定程度上起到去噪的效果。
10.4 核化线性降维
线性降维方法假设从高维空间到低维空间的函数映射是线性的,然而,在不少现实任务中,可能需要非线性映射才能找到恰当的低维嵌入。图10.6给出了一个例子,样本点从二维空间中的矩形区域采样后以S形曲面嵌入到三维空间,若直接使用线性降维方法对三维空间观察到的样本点进行降维,则将丢失原本的低维结构。为了对“原本采样的”低维空间与降维后的低维空间加以区别,我们称前者为“本真”(intrinsic)低维空间。

10.5 流形学习
流形学习(manifold learning)是一类借鉴了拓扑流形概念的降维方法“流形”是在局部与欧氏空间同胚的空间,换言之,它在局部具有欧氏空间的性质,能用欧氏距离来进行距离计算。这给降维方法带来了很大的启发:若低维流形嵌入到高维空间中,则数据样本在高维空间的分布虽然看上去非常复杂但在局部上仍具有欧氏空间的性质,因此,可以容易地在局部建立降维映射关系,然后再设法将局部映射关系推广到全局。当维数被降至二维或三维时,能对数据进行可视化展示,因此流形学习也可被用于可视化。
10.5.1 等度量映射
等度量映射(Isometric Mapping,简称Isomap)的基本出发点,是认为低维流形嵌入到高维空间之后,直接在高维空间中计算直线距离具有误导性,因为高维空间中的直线距离在低维嵌入流形上是不可达的如图 10.7(a)所示,低维嵌入流形上两点间的距离是“测地线”(geodesic)距离想象一只虫子从一点爬到另一点,如果它不能脱离曲面行走,那么图10.7(a)中的红色曲线是距离最短的路径,即S曲面上的测地线,测地线距离是两点之间的本真距离。显然,直接在高维空间中计算直线距离是不恰当的

在近邻连接图上计算两点间的最短路径,可采用著名的Diikstra算法或Floyd 算法,在得到任意两点的距离之后,就可通过 10.2节介绍的 MDS 方法来获得样本点在低维空间中的坐标。图10.8给出了Isomap 算法描述

Isomap仅是得到了训练样本在低维空间的坐标,对于新样本如何将其映射到低维空间呢?这个问题的常用解决方案,是将训练样本的高维空间坐标作为输入、低维空间坐标作为输出,训练一个回归学习器来对新样本的低维空间坐标进行预测,这显然仅是一个权宜之计,但目前似乎并没有更好的办法。
对近邻图的构建通常有两种做法,一种是指定近邻点个数,例如欧氏距离最近的 k k k个点为近邻点,这样得到的近邻图称为 k k k近邻图;另一种是指定距离阈值 ϵ \epsilon ϵ,距离小于 ϵ \epsilon ϵ的点被认为是近邻点,这样得到的近邻图称为 ϵ \epsilon ϵ近邻图。两种方式均有不足,例如若近邻范围指定得较大,则距离很远的点可能被误认为近邻,这样就出现“短路”问题:近邻范围指定得较小,则图中有些区域可能与其他区域不存在连接,这样就出现“断路”问题。短路与断路都会给后续的最短路径计算造成误导
10.5.2 局部线性嵌入
与Isomap试图保持近邻样本之间的距离不同,局部线性嵌入(LocallyLinear Embedding,简称LLE)试图保持邻域内样本之间的线性关系,如图10.9所示,假定样本点 x i x_i xi的坐标可以通过它的邻域样本 x j x_j xj, x k x_k xk, x l x_l xl的坐标通过线性组合来表示,即
x i = w i j x j + w i k x k + w i l x l x_i=w_{ij}x_j+w_{ik}x_k+w_{il}x_l xi=wijxj+wikxk+wilxl

LLE先为每个样本KaTeX parse error: Expected group after '_' at position 2: x_̲找到其近邻下标集合 Q i Q_i Qi,然后计算出基于 Q i Q_i Qi;中的样本点 x i x_i xi对;进行线性重构的系数 w i w_i wi:
w i j = ∑ k ∈ Q i C j k − 1 ∑ l , s ∈ Q i C l s − 1 w_{ij}=\frac{\sum_{k\in Q_i}C_{jk}^{-1}}{\sum _{l,s\in Q_i}C_{ls}^{-1}} wij=∑l,s∈QiCls−1∑k∈QiCjk−1
然后去求解低维坐标:
Z = ( z 1 , z 2 , ⋯ , z m ) ∈ R d ′ ∗ m , ( W ) i j = w i j Z=(z_1,z_2,\cdots,z_m)\in {R}^{{d}'*m},(W)_{ij}=w_{ij} Z=(z1,z2,⋯,zm)∈Rd′∗m,(W)ij=wij
M = ( I − W ) T ( I − W ) M=(I-W)^T(I-W) M=(I−W)T(I−W)
最后可以得到:
KaTeX parse error: Undefined control sequence: \; at position 19: …nderset{z}{min}\̲;̲ \; tr(ZMZ^T)\;…
LLE 的算法描述如图 10.10所示。

10.6 度量学习
在机器学习中,对高维数据进行降维的主要目的是希望找到一个合适的低维空间,在此空间中进行学习能比原始空间性能更好。事实上,每个空间对应了在样本属性上定义的一个距离度量,而寻找合适的空间,实质上就是在寻找一个合适的距离度量。那么,为何不直接尝试“学习”出一个合适的距离度量呢?这就是度量学习(metric learning)的基本动机。
对两个 d d d维样本 x i x_i xi和 x j x_j xj,,它们之间的平方欧氏距离可写为
d i s t e d 2 ( x i , x j ) = ∣ ∣ x i − x j ∣ ∣ 2 2 = d i s t i j , 1 2 + d i s t i j , 2 2 + ⋯ + d i s t i j , d 2 dist_{ed}^{2}(x_{i},x_{j})=||x_{i}-x_{j}||_{2}^{2}=dist_{ij,1}^{2}+dist_{ij,2}^{2}+\cdots+dist_{ij,d}^{2} disted2(xi,xj)=∣∣xi−xj∣∣22=distij,12+distij,22+⋯+distij,d2
其中 d i s t i j , k dist_{ij,k} distij,k表示 x i x_i xi与 x j x_j xj,在第k维上的距离。若假定不同属性的重要性不同,则可引入属性权重 w w w,得到:
d i s t w e d 2 ( x i , x j ) = ∣ ∣ x i − x j ∣ ∣ 2 2 = w 1 ⋅ d i s t i j , 1 2 + w 2 ⋅ d i s t i j , 2 2 + ⋯ + w d ⋅ d i s t i j , d 2 = ( x i − x j ) T W ( x i − x j ) dist_{wed}^{2}(x_{i},x_{j})=||x_{i}-x_{j}||_{2}^{2}=w_{1}\cdot dist_{ij,1}^{2}+w_{2}\cdot dist_{ij,2}^{2}+\cdots+w_{d}\cdot dist_{ij,d}^{2} =(x_{i}-x_{j})^{T}W(x_{i}-x_{j}) distwed2(xi,xj)=∣∣xi−xj∣∣22=w1⋅distij,12+w2⋅distij,22+⋯+wd⋅distij,d2=(xi−xj)TW(xi−xj)
其中 w i ≥ 0 w_i≥0 wi≥0, W = d i a g ( w ) W=diag(w) W=diag(w)是一个对角矩阵, ( W ) i i = w i (W)ii=w_i (W)ii=wi。
式(1033)中的 W W W可通过学习确定,但我们还能再往前走一步: W W W的非对角元素均为零,这意味着坐标轴是正交的,即属性之间无关;但现实问题中往往不是这样,例如考虑西瓜的“重量”和“体积”这两个属性,它们显然是正相关的,其对应的坐标轴不再正交。为此,将式(1033)中的 W W W替换为一个普通的半正定对称矩阵 M M M,于是就得到了马氏距离(Mahalanobis distance)
d i s t m a h 2 ( x i , x j ) = ( x i − x j ) T M ( x i − x j ) = ∣ ∣ x i − x j ∣ ∣ M 2 dist_{mah}^{2}(x_{i},x_{j})=(x_{i}-x_{j})^{T}M(x_{i}-x_{j})=||x_{i}-x_{j}||_{M}^{2} distmah2(xi,xj)=(xi−xj)TM(xi−xj)=∣∣xi−xj∣∣M2
其中 M M M亦称“度量矩阵”,而度量学习则是对 M M M进行学习。注意到为了保持距离非负且对称, M M M必须是(半)正定对称矩阵,即必有正交基 P P P使得 M M M能写为 M = P P T M=PP^T M=PPT
对M进行学习当然要设置一个目标。假定我们是希望提高近邻分类器的性能,则可将M直接嵌入到近邻分类器的评价指标中去,通过优化该性能指标相应地求得M。
相关文章:

机器学习 第10章-降维与度量学习
机器学习 第10章-降维与度量学习 10.1 k近邻学习 k近邻(k-Nearest Neighbor,简称kNN)学习是一种常用的监督学习方法其工作机制非常简单:给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个“邻居”的信息来进行预测。通…...
物理地址到虚拟地址映射)
linux驱动:(7)物理地址到虚拟地址映射
单片机、裸机、linux操控硬件方法 在单片机和裸机中操作硬件是通过指针来对寄存器赋值来进行操控 但对于linux中不能这样,不能直接对物理地址直接修改,因为linux使能了mmu,所以不能直接菜操作物理地址 如果要操作硬件,需要先把…...

浏览器用户文件夹详解 - Preferences(十)
1.Preferences简介 1.1 什么是Preferences文件? Preferences文件是Chromium浏览器中用于存储用户个性化设置和配置的一个重要文件。每当用户在浏览器中更改设置或安装扩展程序时,这些信息都会被记录在Preferences文件中。通过这些记录,浏览…...

Robot Operating System——电池电量通知
大纲 应用场景定义字段解释 案例 sensor_msgs::msg::BatteryState 是 ROS 2 中定义的消息类型,用于表示电池状态。它包含了电池电量、电压、电流、温度等信息。 应用场景 机器人 电池监控:在移动机器人中,电池是主要的电源。BatteryState 消…...

二进制安装docker
目录 一、准备 Docker CE 二进制包 二、解压.tgz包 三、复制二进制文件到/usr/bin/目录 四、创建用户组 五、配置相关服务配置文件 六、拷贝配置文件到指定目录 七、启动 dockerd 服务进程 八、shell脚本一键安装 一、准备 Docker CE 二进制包 https://download.docker…...

@SpringBootConfiguration重复加载报错
Junit单元测试Test启动报错,SpringBootConfiguration注解重复问题排查: SpringBootApplication 注解的 exclude 属性用于排除特定的自动配置类,而不是用于排除主配置类本身。因此,不能通过 exclude 属性来排除主配置类的加载。 …...

【SpringBoot】数据验证之分组校验
分组校验 在不同情况下,可能对JavaBean对象的数据校验规则有所不同,有时需要根据数据状态对JavaBean中的某些属性字段进行单独验证。这时就可以使用分组校验功能,即根据状态启用一组约束。 Hibernate Validator的注解提供了groups参数&#…...

MySQL Galera Cluster 部署与介绍
目录 主要特点 组件 一. 环境准备 二. 配置 1. 配置 galera1 主机的my.cnf的文件 2. 配置 galera2 主机的my.cnf的文件 3. 配置 galera3 主机的my.cnf的文件 4. 在给galera1 主机的my.cnf的文件增加节点 5. 写入数据验证同步 6. 配置 galera4 主机的my.cnf的文件 M…...

RuoYi-Vue-Plus (XXL-JOB任务调度中心二:配置管理与定时任务编写、执行策略、命令行任务、邮件报警等等
一、后端xxl job的配置属性介绍 enabled : 是否开启执行器,如果为false,调度中心就调用不了后端定时任务admin-addresses:调度中心的地址,多个则可以逗号拼接: url1,url2,url3access-token: 执行器通讯TOKEN ,必须和x…...

【docker】虚拟化与docker基础
一、虚拟化 1.虚拟化概述 什么是虚拟化? 虚拟化:将应用程序和系统内核资源进行解耦,以操作系统级别进行隔离,目的是提高资源利用率 2、虚拟化的功能 将虚拟化的性能优化趋近于物理资源的性能,主要用于提高资源利用…...

Vue3安装ffmpeg做视频截取报错
通过 yarn 安装 ffmpeg 时报错。 即,执行以下指令时报错: yarn add ffmpeg/ffmpeg^0.10.0 yarn add ffmpeg/core^0.10.0错误信息: node_modules\pngquant-bin: Command failed. Error: pngquant failed to build, make sure that libpng-d…...

如何在 Java 中实现自定义的排序算法?
在Java中实现自定义排序算法的步骤如下: 创建一个类,实现Java的Comparator接口,该接口包含一个compare方法,用于比较两个对象的大小。在compare方法中,根据自定义的排序规则,比较两个对象的大小并返回-1、…...

【Homebrew】brew 命令
Brew(也称为Homebrew)是Mac OS上的一款包管理器,它允许用户通过简单的命令行界面来安装、更新、卸载和管理软件包。以下是一些常用的Brew命令及其功能说明: 安装与卸载 安装Brew 命令(适用于大多数用户,可…...

【https】无法安装OpenSSL时如何在局域网开通https服务
【背景】 做Stream传输服务,需要用到fetch方法,所以自然也需要https服务。 公司的开发机由于某些管理上的原因无法直接安装openssl for win的安装包。 【分析】 没有命令行工具,就试试看万能的python包吧,直接安装cryptography包。 pip install cryptography【方法】 …...

OpenGL实现3D游戏编程【连载1】——初探3D世界
1、前言 在我学习C的过程中,研究了一下OpenGL编程,打开了3D世界的编程世界,3D世界的效果还是相当不错。而且OpenGL能够支持跨平台兼容,是不错的学习方向,于是就自己学习了网上的很多教程,并将所有学到的知…...
工程化实践:工程配置化设计
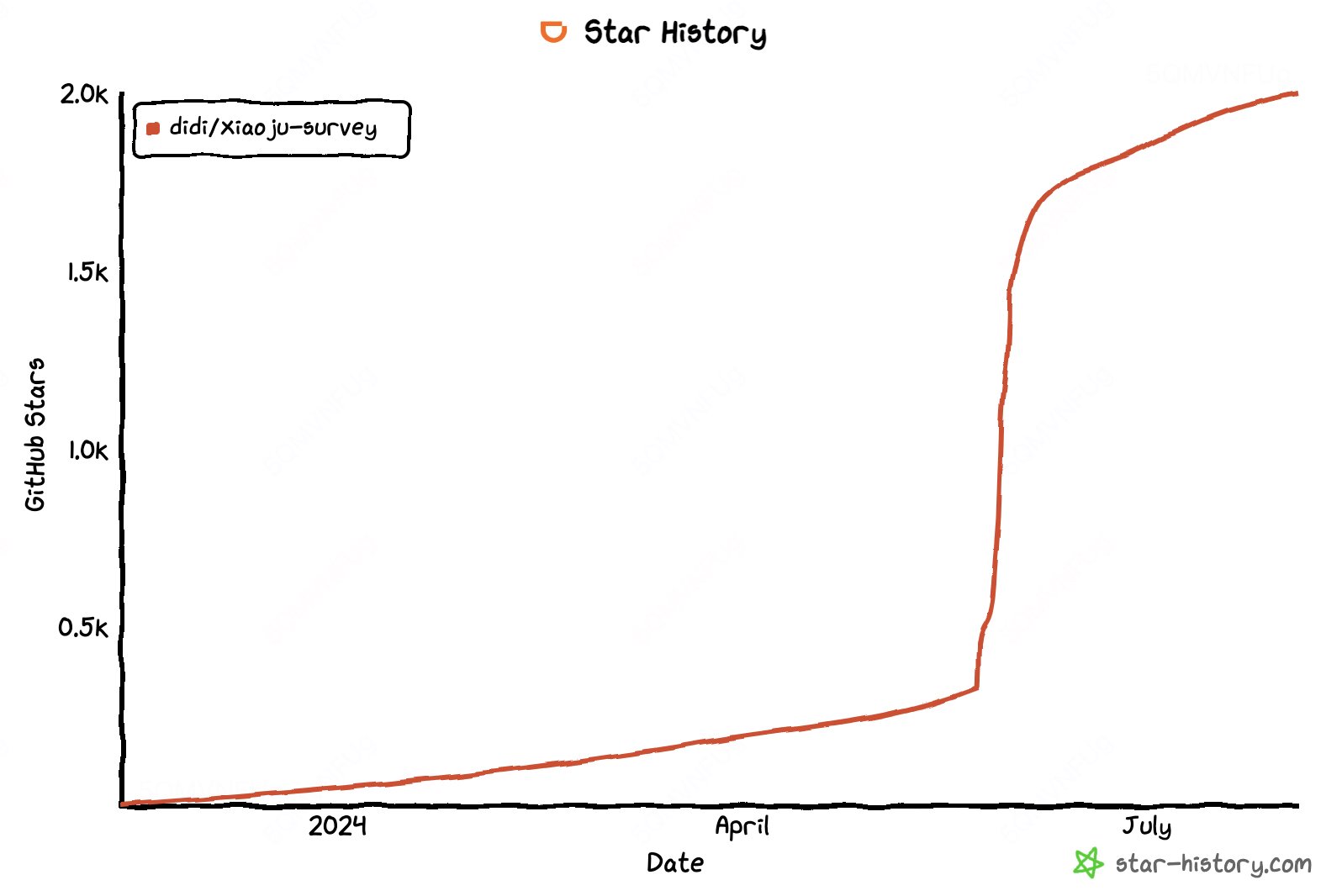
文内项目 Github:XIAOJUSURVEY 配置化是很灵活且很常见的使用,那XIAOJUSURVEY里有哪些地方应用到了呢? 基础模板 问卷模板 在创建问卷时,我们提供了多种问卷类型选择,例如普通问卷、投票、报名、NPS等。 为了实…...

浏览器事件循环详解
1. 浏览器的进程模型 1.1. 何为进程? 程序运行需要有它自己的专属内存空间,可以把这块内存空间简单的理解为进程。 每个应用至少有一个进程,进程之间相互独立,即使要通信,也需要双方同意。 1.2. 何为线程?…...
)
Linux:线程管理(线程创建、线程退出、线程回收、线程分离、其它线程函数)
线程管理 (1)What(什么是线程管理) 对程序中线程的创建、调度、同步、退出、回收等操作进行有效的控制和协调 (2)Why(为什么要管理线程) 充分利用系统资源,提高程序的并发的性能和稳定性。但如果管理不当,…...

【JVM】常见面试题
🥰🥰🥰来都来了,不妨点个关注叭! 👉博客主页:欢迎各位大佬!👈 文章目录 1. JVM 中的内存区域划分2. JVM 的类加载机制2.1 加载(Loading)✨双亲委派模型2.2 验证(Verification)2.3 准…...

0805作业+梳理
一、作业: 代码: create.c #include<myhead.h> int main(int argc, const char *argv[]) {//创建一个有名管道文件if(mkfifo("./linux",0664)-1){perror("mkfifo linux error");return -1;}getchar();system("rm linux…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
