数据结构(其四)--特殊矩阵的存储
目录
11.特殊矩阵的压缩存储
(1).一维数组的储存结构
(2).二维数组的存储结构
(3).普通矩阵的存储
(4).特殊矩阵的压缩存储
i.对称矩阵
ii.三角矩阵
iii.三对角矩阵
iiii.稀疏矩阵
11.特殊矩阵的压缩存储
(1).一维数组的储存结构
int a[10];
一维数组的地址是连续的,只要知道了起始地址(LOC,默认是a[0]的地址),就可以知道所有元素的地址。

a[i] 地址的计算 :LOC + i * sizeof(int) .
注意:有时候给出的LOC可能不是a[0] 的,此时,就要在上式子的i 中减去,如给出的是a[1]的,则计算公式变为 LOC + (i - 1) * sizeof(int).
(2).二维数组的存储结构
int b[2][4]
二维数组在内存中有两种存储方法,行优先和列优先。

当然,从逻辑视角上看,将数据配列成矩阵的样式,更方便进行操作。
有int b[M][N],b[0][0] 的地址为LOC,则b[i][j]
行优先:LOC + (i*N + j)*sizeof(int)
列优先:LOC + (j*M + i)*sizeof(int)
(3).普通矩阵的存储
一般是用二维数组,
需要注意的是,矩阵的下标是从(1, 1) 开始的,数组是从(0, 0) 开始的。
(4).特殊矩阵的压缩存储
i.对称矩阵
· 是方阵(n阶),
· 恒有 aij == aji,
因为对称,所以可以只存储下三角区和对称轴(或上三角区和对称轴)(这样就是所谓的压缩存储)

按行优先将各元素存入一维数组(也可以列优先),
如此便要思考,
数组的大小,显然,第一行一个元素,第二行两个元素...第N行N个元素,总数就是n*(n+1)/2.
数据的调用,因为矩阵的下标与数组的下标规则不同,可以写一个简单的映射函数进行转换
aij => b[k]
总结上图,可知
k = (i+1)*i/2 + j - 1 ,
即当前元素行数往上为等差数列求和,再加上列数,就是在数组中的第几个元素,再减一,就成了数组下标。(如果,题干给出的数组起始下标为1,k就不需要减去那个1)
ii.三角矩阵

压缩存储策略:储存aij的三角区,将常数储存在数组最后一位。(以下三角为例)
数组大小,n*(n+1)/2 + 1.
aij的ij 与数组下标之间的相互转换与上文相同。
获取常数项,数组下标就是 n*(n+1)/2。
值得一提的,在上三角中,求aij是数组中的第几个元素,观察图可知,每行的元素数由N个依次递减。所以,aij 前面有 [n + ... + (n - i + 2)] + (j - i)个元素,中括号里的是此行往上的,那个j-i是当前行内aij 之前的元素。
iii.三对角矩阵

以行优先为例,
数组大小,3n - 2。
数组下标(对于aij),前(i - 1)行,有3(i - 1) - 1个元素(每行有三个元素,但第一行只有两个);第i 行中,aij是第j - i + 2个元素,所以aij 就是第2i + j - 2(前后相加)。
k = 2i + j - 3
由数组下标逆推矩阵下标ij
已知b[k]
是第k + 1个元素,在前i-1行,与前i行之间,3(i - 1) - 1 < k + 1 <= 3i - 1
i >= (k + 2)/3,左式算出结果后向上取整就是i 值
(向上取整:如1.2,向上取整就是2,向下就是1)
iiii.稀疏矩阵

压缩策略:
① 顺序存储------设置一个类,其中包含三个数组,分别存储i、j、非零数据。
② 十字链表法----此为链式存储,

结点中,包含行、列、值以及两个指针。
两个指针分别指向同一列的下一个结点和同一行的下一个结点。
相关文章:

数据结构(其四)--特殊矩阵的存储
目录 11.特殊矩阵的压缩存储 (1).一维数组的储存结构 (2).二维数组的存储结构 (3).普通矩阵的存储 (4).特殊矩阵的压缩存储 i.对称矩阵 ii.三角矩阵 iii.三对角矩阵 iiii.稀疏矩…...

系统化学习 H264视频编码(06)哥伦布编码
说明:我们参考黄金圈学习法(什么是黄金圈法则?->模型 黄金圈法则,本文使用:why-what)来学习音H264视频编码。本系列文章侧重于理解视频编码的知识体系和实践方法,理论方面会更多地讲清楚 音视频中概念的…...

手机在网状态接口如何对接?(一)
一、什么是手机在网状态? 传入手机号码,查询该手机号的在网状态,返回内容有正常使用、停机、在网但不可用、不在网(销号/未启用/异常)、预销户等多种状态。 二、手机在网状态使用场景? 1.信贷审核&#…...

数据结构链表2(常考习题1)(C语言)
移除链表元素: . - 力扣(LeetCode) 题目: 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 解题思路: 情况1: 情…...

Rust的运行时多态
Rust的运行时多态 Rust的静态多态即编译时多态,通过**泛型特征约束(Generic Type Trait Constrait)**来实现; 那么动态多态(运行时多态)呢?答案是特征对象(Trait Objectÿ…...

sqllabs通关
sqllabs5:(报错注入) ?id1 回显You are in........... ?id2-1 回显You are in........... ?id1 回显 1 LIMIT 0,1 判断是字符型,闭合。?id1order by 3-- //页面显示正常我们试了4行得出是报错注入 我们先爆库名 http://127.0.0.1/sqli-labs-master/L…...
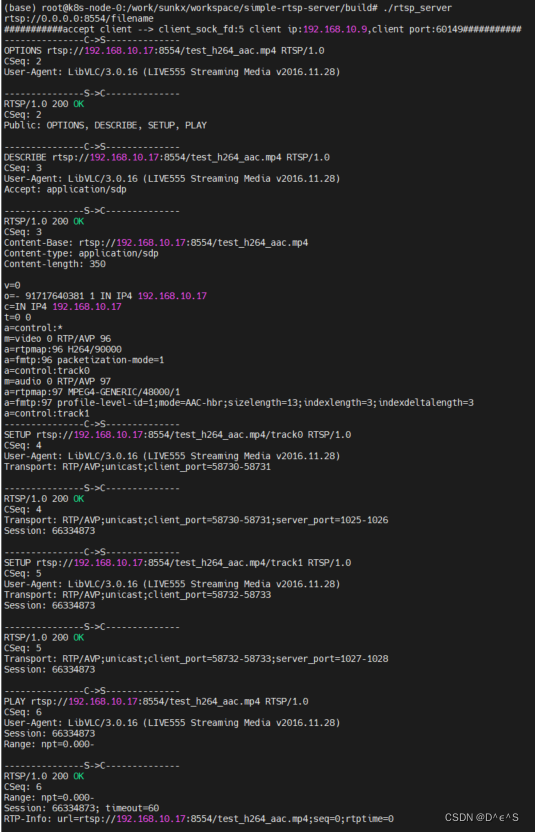
RTSP系列四:RTSP Server/Client实战项目
RTSP系列: RTSP系列一:RTSP协议介绍-CSDN博客 RTSP系列二:RTSP协议鉴权-CSDN博客 RTSP系列三:RTP协议介绍-CSDN博客 RTSP系列四:RTSP Server/Client实战项目-CSDN博客 目录 一、RTSP Server实战项目 1、准备 2、…...

sqli-labs-php7-master第11-16关
猜注入点 先来猜数字型 单引号字符型: 发现注入点找到了 猜测数据库有多少个字段: 1’ order by 4 # 密码随便输的。 这里没有使用--注释,因为没作用,可能是过滤掉了 继续猜。刚才没猜对 1 order by 2 # 没报错,猜…...

c++初阶 string的底层实现
string 基础函数成员成员变量构造函数析构函数:拷贝构造赋值构造 遍历下标访问迭代器 增删插开辟空间push_backappendinserterase 功能函数swapfindc_strsubstrclear 其他函数比较函数流提取<<流插入>>getline 完整版 声明:非纯手搓…...

微信小程序实现上传照片功能
案例: html: <view class"zhengjianCont fontSize30" style"margin-bottom: 40rpx;"><view class"kuai"><image binderror"imageOnloadError" bind:tap"upladPhoto" data-params"business…...

lombok安装成功但是找不到方法
2024.1.1版本的IDE的插件安装了默认的lombok(如图1),pom文件中也引入了lombok的依赖,在实体类写了Data的注解,当调用实体类的get和set方法运行时,报错找不到相应的方法,但是在调用get、set方法的…...

单细胞Seurat的umi矩阵-与feature、counts(用于质控)
目录 关于umi矩阵学习 用umi计算feature、counts值 ①meta数据查看 ②Count和Feature计算(生成Seurat时自动计算) 1)提取UMI矩阵 2)计算 其他指标 评估质量指标(重点) 1)UMI计数 2)基因计数 3)UMIs vs. genes detected 4)线粒体计数比率 5)综合过滤 过…...
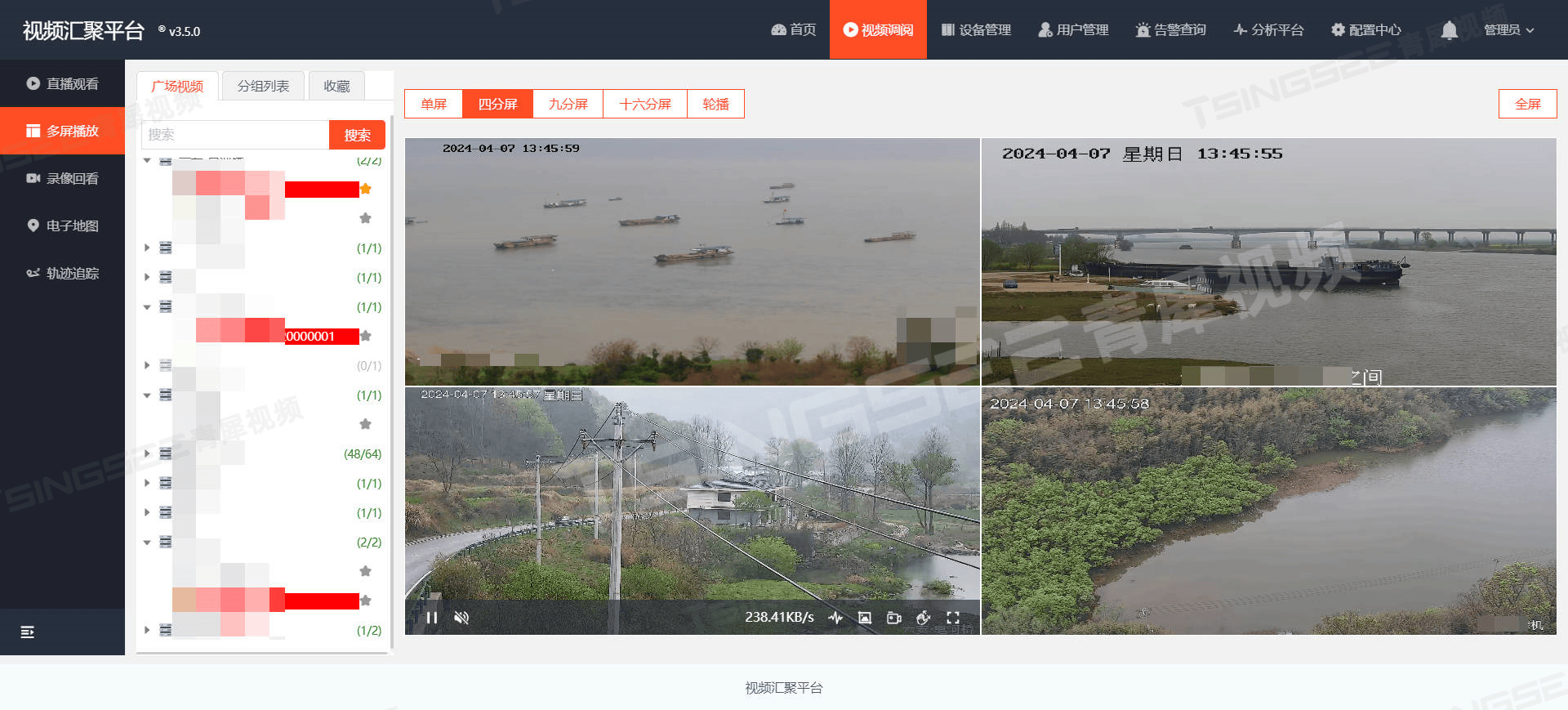
安防视频监控EasyCVR视频汇聚平台设备发送了GPS位置,但是订阅轨迹为空是什么原因?
安防视频监控EasyCVR视频汇聚平台兼容性强、支持灵活拓展,平台可提供视频远程监控、录像、存储与回放、视频转码、视频快照、告警、云台控制、语音对讲、GIS地图、轨迹跟踪、平台级联等视频能力。 用户描述,设备在电子地图中可以查看到定位信息ÿ…...

在 VueJS 中使用事件委托处理点击事件(事件委托,vue事件委托,什么是事件委托,什么是vue的事件委托)
前言 在开发 Vue 项目时,我们经常需要处理大量的点击事件。为每个可点击的元素单独添加事件监听器不仅会增加代码的复杂度,还会降低性能。事件委托是一种有效的优化方式,它可以显著减少事件监听器的数量,提高代码的可维护性和执行…...

密码学简史:时间密语
注:机翻,未校。 A brief history of cryptography: Sending secret messages throughout time Stemming from the Greek words for “hidden writing,” cryptography is the practice of encrypting transmitted information so that it can only b…...

【Java数据结构】---初始数据结构
乐观学习,乐观生活,才能不断前进啊!!! 我的主页:optimistic_chen 我的专栏:c语言 ,Java 欢迎大家访问~ 创作不易,大佬们点赞鼓励下吧~ 前言 从今天开始我们就要学习Java…...

MySQL--主从复制
前言:本博客仅作记录学习使用,部分图片出自网络,如有侵犯您的权益,请联系删除 一、什么是主从复制 1、定义 主从复制,是用来建立一个和主数据库完全一样的数据库环境,称为从数据库;主数据库一…...

Linux RT调度器之负载均衡
RT调度类的调度策略是:保证TopN(N为系统cpu个数)优先级的任务可以优先获得cpu资源。除了在任务选核时通过基于cpu优先级的选核策略保证这一点外,还有其它流程,我们姑且将这部分流程称作RT调度器的负载均衡(…...
--初识Pwn沙箱)
pwn学习笔记(8)--初识Pwn沙箱
初识Pwn沙箱 沙箱机制,英文sandbox,是计算机领域的虚拟技术,常见于安全方向。一般说来,我们会将不受信任的软件放在沙箱中运行,一旦该软件有恶意行为,则禁止该程序的进一步运行,不会对真实系…...
基础入门学习)
Day18_2--Vue.js Ajax(使用 Axios)基础入门学习
Vue.js 中的 Ajax 请求(使用 Axios) 什么是 Axios? Axios 是一个基于 Promise 的 HTTP 客户端,可以用于浏览器和 Node.js 环境中。它是现代化的 Ajax 库,用来替代传统的 XMLHttpRequest。 为什么选择 Axios…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
