虚拟机类加载机制
与那些编译时需要进行连接的语言不同,在java语言中,类型的
动态加载:编写一个面向接口的应用程序,可以等到运行时再指定其实现类。
类加载:加载-连接-初始化-使用-卸载
一个类被调用时,会将其class文件从磁盘中加载到虚拟机中。
加载
(1)通过一个类的全限定名来获取定义此类的二进制字节流。
(2)将这个流转换为方法区的静态文件结构。
(3)在内存中生成Class对象,作为方法区的访问入口。
连接的过程
先验证class文件的安全性,然后开辟类变量的空间和位置,将常量池中的符号引用替换为直接引用。
初始化
初始化阶段就是执行类构造器()方法的过程。
()是javac编译器自动生成的产物。
()是类中的所有类变量的赋值当作和静态static块语句合并产生的,按照程序顺序生成。
类加载器
根据类的全限定名获取所需要的类。
对于任意一个类,都必须由加载它的类加载器和这个类本身一起确认其唯一性。对于每一个类加载器,都有一个独立的类名称空间。这里的唯一性,体现在equals()方法,isInstance()方法。
启动类加载器:加载<java_home>/lib目录的java核心类
扩展类加载器:加载<java_home>/lib/ext目录下的类库
应用程序类加载器:是ClassLoader.getSystemClassLoader()方法的返回值,加载用户路径上的类,即用户自己写的类
双亲委派:如果一个类加载器加载类,会先委派给启动类加载器,然后是扩展类加载器,发现类不在其加载路径上,才会由应用类加载器加载
相关文章:

虚拟机类加载机制
与那些编译时需要进行连接的语言不同,在java语言中,类型的 动态加载:编写一个面向接口的应用程序,可以等到运行时再指定其实现类。 类加载:加载-连接-初始化-使用-卸载 一个类被调用时,会将其class文件从…...
——逐月筛选影像,并给影像集合添加新的属性)
Google Earth Engine(GEE)——逐月筛选影像,并给影像集合添加新的属性
简介 导入影像集合首先,您需要导入您要筛选的影像集合。使用Google Earth Engine的ImageCollection类来导入影像集合。您可以通过ee.ImageCollection()函数传递影像集合的ID或通过一个ee.ImageCollection()对象导入影像集合。 例如,导入Landsat 8卫星每月影像集合的代码如下…...
如何从智联招聘网站快速抓取职位详情?两大技巧揭秘
摘要: 本文将揭秘如何利用Python爬虫技术,高效且合法地从智联招聘网站抓取职位详情信息。通过实战示例,展现两大核心技巧,助你在大数据时代抢占先机,为你的市场分析、人才研究提供强大支持。 一、引言:数据…...

C#知识|ini文件操作
哈喽,你好啊,我是雷工! 本节学习ini文件的操作,之前练习过通过ini文件导出采集模块的配置信息,然后再另一个模块中导入配置信息,如此实现快速配置采集模块,提高效率。 以下为学习笔记。 01 认识ini文件 ini文件是一种文件格式,类似txt,xml等, ini文件在上位机开发中使…...

Linux系统学习之路
一、Linux基础训练 https://mp.weixin.qq.com/mp/appmsgalbum?actiongetalbum&__bizMzUxNjMwMzk4MQ&scene1&album_id3544800080551952390&count3#wechat_redirect...

DNS介绍与部署-Day 01
1. 什么是DNS DNS(Domain Name System)域名系统,是一种采用客户端/服务器机制,负责实现计算机名称与IP地址转换的系统。DNS作为一种重要的网络服务,既是Internet工作的基础,同时在企业内部网络中也得到了广…...

python 图片爬虫记录
感谢大家的点赞。再补充一点。 对于这个 url https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjEqB5nighYsMZE7kexaVNJfxy3OkRutNEKatksw9u5f-ckHNROLzFyx2Uty3zYWNEaeOmzsljGr3eARiDWaM9DM8G2hPuPf8uZP0NO3kNUCnM2Cjb3ZKtLhJDBwqeR4ElpJ7ID5_wIHGQ/s200 这个url最…...

本地安装Llama3.1与LobeChat可视化UI界面并实现远程访问大模型实战
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

MSF回弹木马在Ubuntu中测试
1.创建文件 网站地址为192.168.30.129 首先在Ubuntu中use/local/nginx/sbin路径下创建一个PHP文件; 如图所示: 然后进入网页下载PHP文件如图所示: 什么都不显示说明这个没有问题就怕访问失败。 2.使用蚂键连接网站 在蚂键中的URL地址栏中…...

大数据等保测评
在当今数字化浪潮汹涌澎湃的时代,大数据已成为企业和组织创新发展的核心驱动力。然而,随着大数据应用的日益广泛和深入,其安全问题也日益凸显。大数据等保测评作为保障大数据安全的重要手段,具有至关重要的意义。 大数据的特点决定…...

CSS对元素的分类
文章目录 概述置换元素/非置换元素置换元素非置换元素 行内元素/块级元素/行内块级元素行内元素块级元素行内块级元素 概述 CSS从两个维度上将HTML元素进行了分类: 从元素内容的表现形式上,将元素分为:置换元素、非置换元素。从元素自身的显…...
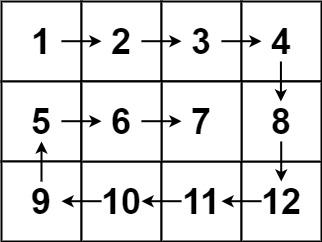
力扣第五十四题——螺旋矩阵
内容介绍 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2: 输入:matrix …...

中创算力:以知识产权转化运用促进高质量发展
创新是引领发展的第一动力,保护知识产权就是保护创新。为深入实施知识产权公共服务普惠工程,促进知识产权公共服务更好服务高水平科技,国家知识产权局发布关于全面提升知识产权公共服务效能的指导意见。 在政策落地过程中,如何精…...

C语言9~10 DAY(合集)
数组的概念 什么是数组 数组是相同类型,有序数据的集合。 数组的特征 数组中的数据被称为数组的元素,是同构的 数组中的元素存放在内存空间里 (char player_name[6]:申请在内存中开辟6块连续的基于char类型的变量空间) 衍生概念&#x…...

【Kubernetes】应用的部署(一):金丝雀部署
应用的部署(一):金丝雀部署 在项目迭代开发过程中,经常需要对应用进行上线部署。上线部署策略主要有 3 种:金丝雀部署、蓝绿部署 和 滚动部署。 金丝雀部署 也被叫作 灰度部署。金丝雀部署过程:先让一部分…...

1.面试准备篇
筛选简历 找实习用处不大 简历注意事项 注意职业技能和项目经历 职业技能 黄金位置 针对性 引导面试官提问 只写会的 不会的不能写 项目描述 主要设计… 展示指标 找练手项目 来源:Gitee 或者github 主要关注点:功能实现、常见问题、系统设计 面试过程 一面…...

Spring: try-catch 是否还会回滚
问题出现: try-catch 语句 依旧会抛出如下错误 org.springframework.transaction.TransactionSystemException: Could not commit JPA transaction; nested exception is javax.persistence.RollbackException: Transaction marked as rollbackOnlyat org.springf…...

spdlog日志库--基础介绍
文章目录 1. 简介1.1. spdlog代码特点1.2. 说明1.3. spdlog架构 2. spdlog的安装2.1. 使用包管理器安装2.2. 使用源码安装2.3. 仅使用头文件 3. 相关概念3.0 常用的头文件3.1. level_enum3.2. sink3.3. logger3.4 格式输出3.5 对齐方式3.6 截断3.7 字符串格式化fmt 4. 特性4.1.…...
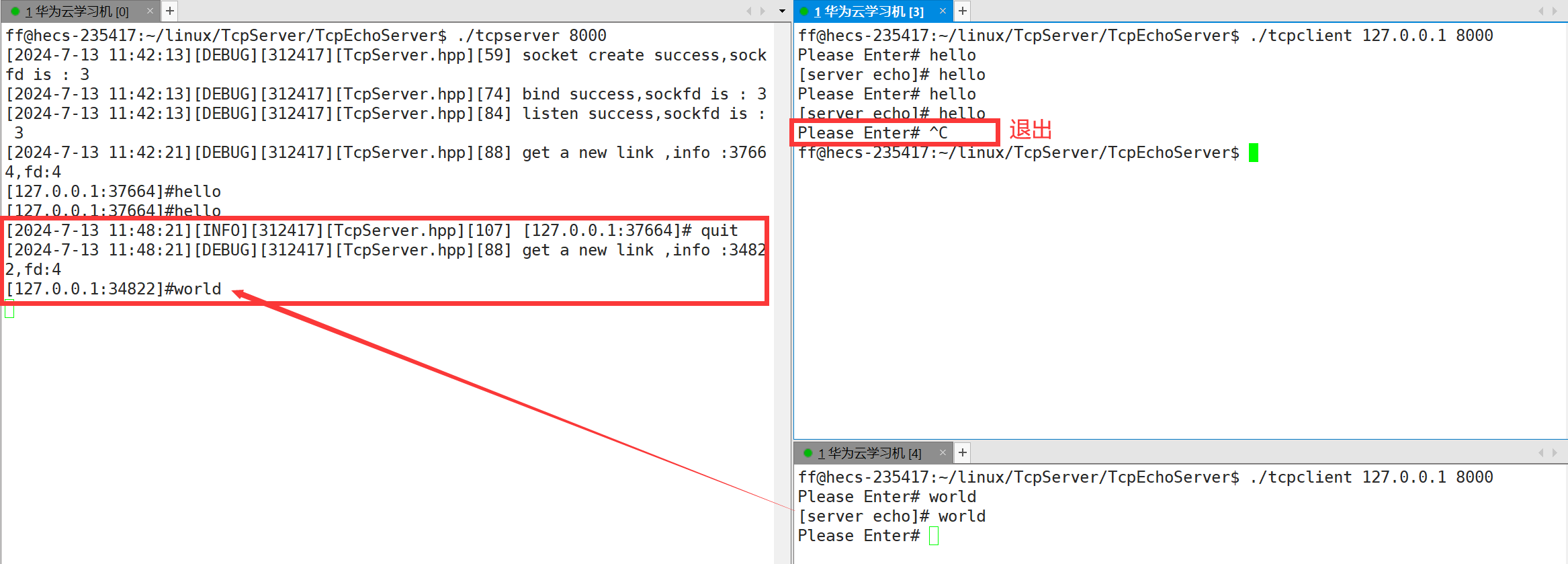
【网络】网络编程套接字(二)
网络编程套接字(二) 文章目录 1.单执行流的TCP网络程序1.1服务端创建套接字1.2服务端绑定1.3服务端监听1.4服务端获取链接1.5服务端处理请求1.6客户端创建套接字1.7客户端连接服务器1.8客户端发起请求 2.多进程版的TCP网络程序2.1单执行流的弊端2.2多进…...
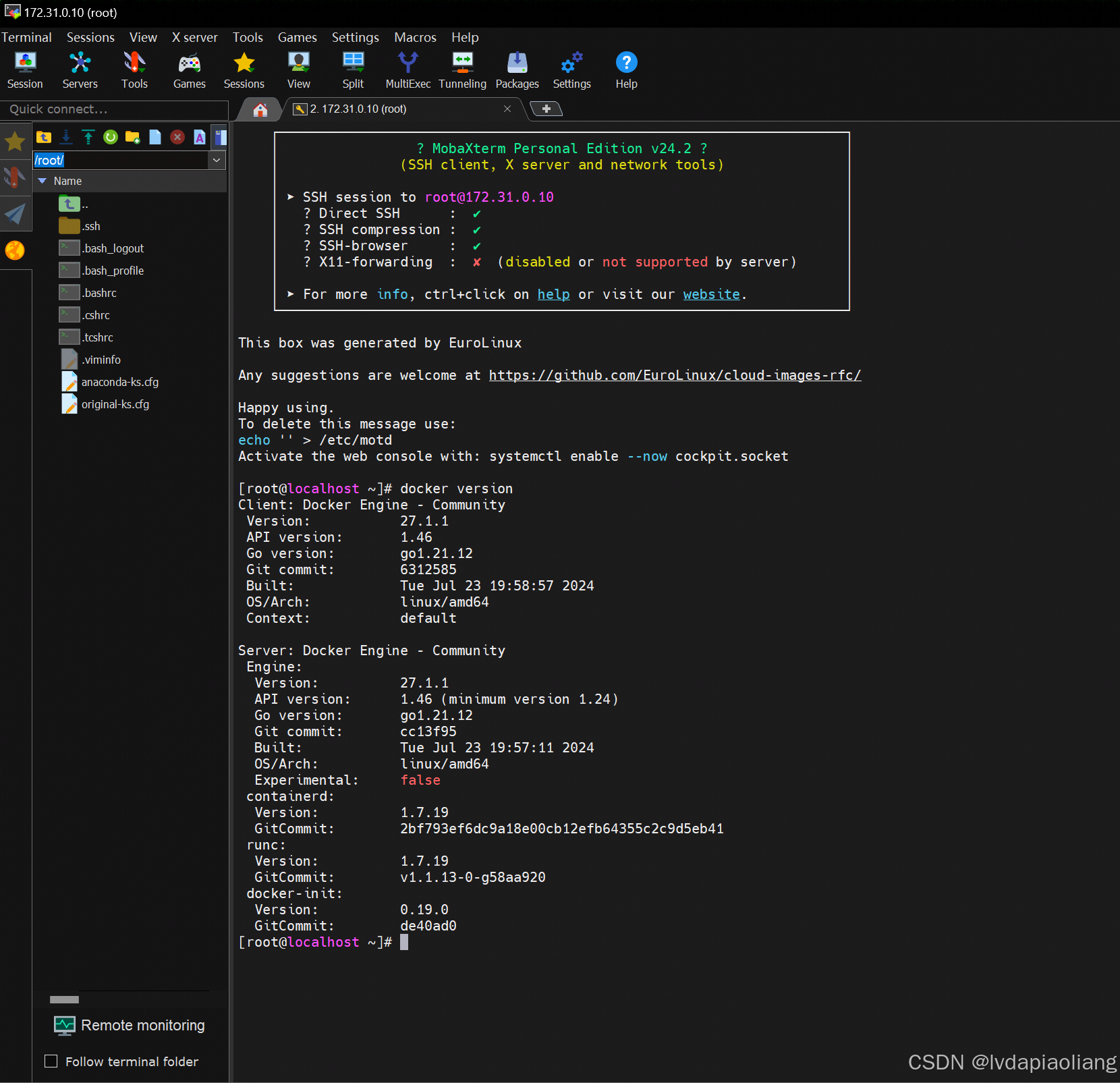
1.1、centos stream 9安装Kubernetes v1.30集群 环境说明
最近正在学习kubernetes,买了一套《Kubernetes权威指南 从Docker到Kubernetes实践全接触(第六版)》这本书讲得很好,上下两册,书中k8s的版本是V1.29,目前官网最新版本是v1.30。强烈建议大家买一套看看。 Kubernetes官网地址&#x…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
