力扣第五十四题——螺旋矩阵
内容介绍
给你一个
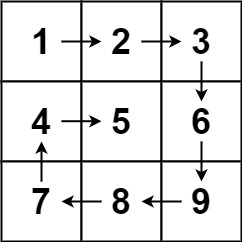
m行n列的矩阵matrix,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。示例 1:
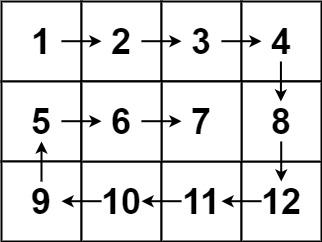
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7]提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
完整代码
int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};int* spiralOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize) {if (matrixSize == 0 || matrixColSize[0] == 0) {*returnSize = 0;return NULL;}int rows = matrixSize, columns = matrixColSize[0];int visited[rows][columns];memset(visited, 0, sizeof(visited));int total = rows * columns;int* order = malloc(sizeof(int) * total);*returnSize = total;int row = 0, column = 0;int directionIndex = 0;for (int i = 0; i < total; i++) {order[i] = matrix[row][column];visited[row][column] = true;int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {directionIndex = (directionIndex + 1) % 4;}row += directions[directionIndex][0];column += directions[directionIndex][1];}return order;
}
思路详解
一、问题背景
给定一个二维数组,要求按照螺旋顺序遍历数组,并返回一个一维数组,其中包含按螺旋顺序遍历得到的元素。
二、解题思路
-
边界处理:
- 首先检查数组是否为空,如果为空,则直接返回空数组。
-
初始化:
- 创建一个二维数组
visited,用于标记数组中已经遍历过的元素。 - 初始化数组的大小为行数乘以列数。
- 创建一个一维数组
order,用于存储按螺旋顺序遍历得到的元素。
- 创建一个二维数组
-
遍历策略:
- 定义一个方向数组
directions,包含四个方向:上、右、下、左。 - 初始化起点
row和column,以及方向索引directionIndex。 - 遍历数组,按照螺旋顺序填充
order数组。 - 在遍历过程中,如果下一个位置越界或者已经遍历过,则改变方向。
- 定义一个方向数组
-
结果返回:
- 遍历完成后,返回
order数组。
- 遍历完成后,返回
三、代码详解
- 边界处理:
- 如果数组为空,直接返回空数组。
if (matrixSize == 0 || matrixColSize[0] == 0) {*returnSize = 0;return NULL;
}
- 初始化:
- 创建
visited数组并初始化为0。 - 创建
order数组并分配内存。 - 初始化
rows、columns、total和directionIndex。
- 创建
int rows = matrixSize, columns = matrixColSize[0];
int visited[rows][columns];
memset(visited, 0, sizeof(visited));
int total = rows * columns;
int* order = malloc(sizeof(int) * total);
*returnSize = total;
- 遍历策略:
- 初始化起点
row和column,以及方向索引directionIndex。 - 遍历数组,按照螺旋顺序填充
order数组。 - 在遍历过程中,如果下一个位置越界或者已经遍历过,则改变方向。
- 初始化起点
int row = 0, column = 0;
int directionIndex = 0;
for (int i = 0; i < total; i++) {order[i] = matrix[row][column];visited[row][column] = true;int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {directionIndex = (directionIndex + 1) % 4;}row += directions[directionIndex][0];column += directions[directionIndex][1];
}
- 结果返回:
- 遍历完成后,返回
order数组。
- 遍历完成后,返回
return order;
四、总结
通过上述步骤,我们能够有效地遍历二维数组并按照螺旋顺序返回一维数组。关键在于正确地初始化数组、遍历策略和结果返回。这种方法的时间复杂度为O(n),其中n为数组的大小。空间复杂度为O(n),用于存储一维数组和二维数组。
知识点精炼
一、核心概念
- 边界条件检查:在开始遍历之前,检查输入的二维数组是否为空。
- 二维数组访问:使用两个索引变量来访问二维数组中的元素。
- 动态数组分配:在内存中动态分配一维数组来存储遍历结果。
- 方向数组:使用一个二维数组来表示遍历的方向。
二、知识点精炼
-
初始化:
- 创建一个二维数组
visited来标记数组中已经遍历过的元素。 - 创建一个一维数组
order来存储按螺旋顺序遍历得到的元素。
- 创建一个二维数组
-
遍历策略:
- 初始化起点
row和column,以及方向索引directionIndex。 - 遍历数组,按照螺旋顺序填充
order数组。 - 在遍历过程中,如果下一个位置越界或者已经遍历过,则改变方向。
- 初始化起点
-
结果返回:
- 遍历完成后,返回
order数组。
- 遍历完成后,返回
三、性能分析
- 时间复杂度:O(n),其中n为数组的大小。
- 空间复杂度:O(n),用于存储一维数组和二维数组。
四、实际应用
- 数据处理:在处理二维数据时,这种算法可以帮助我们按照特定顺序访问数据。
- 算法竞赛:在算法竞赛中,掌握这种算法对于解决与二维数组遍历相关的问题非常有帮助。
五、代码实现要点
- 边界条件检查:确保输入的二维数组不为空。
- 动态数组分配:正确分配内存空间,避免内存泄漏。
- 遍历策略:正确实现螺旋遍历策略,避免数组越界和重复访问。
- 结果返回:正确返回遍历结果。
减少空间复杂度的思路
在原始代码中,我们使用了一个二维数组visited来标记已经遍历过的元素,这导致了较高的空间复杂度。为了减少空间复杂度,我们可以使用一个一维数组来替代二维数组,这样可以将空间复杂度从O(n)降低到O(1)。
以下是优化后的代码:
int* spiralOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize) {if (matrixSize == 0 || matrixColSize[0] == 0) {*returnSize = 0;return NULL;}int rows = matrixSize, columns = matrixColSize[0];int* order = malloc(sizeof(int) * (rows * columns));*returnSize = rows * columns;int top = 0, bottom = rows - 1, left = 0, right = columns - 1;int index = 0;while (top <= bottom && left <= right) {// Traverse the top rowfor (int i = left; i <= right; i++) {order[index++] = matrix[top][i];}top++;// Traverse the rightmost columnfor (int i = top; i <= bottom; i++) {order[index++] = matrix[i][right];}right--;// If there is still a row leftif (top <= bottom) {// Traverse the bottom rowfor (int i = right; i >= left; i--) {order[index++] = matrix[bottom][i];}bottom--;}// If there is still a column leftif (left <= right) {// Traverse the leftmost columnfor (int i = bottom; i >= top; i--) {order[index++] = matrix[i][left];}left++;}}return order;
}
在这个优化版本中,我们使用了一个一维数组order来存储遍历结果,而不是使用一个二维数组visited来标记已经遍历过的元素。我们通过维护四个边界变量(top、bottom、left、right)来控制遍历的方向,并在每次迭代中只遍历尚未访问的部分。这种方法避免了使用额外的空间来存储已访问的元素,从而将空间复杂度降低到O(1)。
相关文章:
力扣第五十四题——螺旋矩阵
内容介绍 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2: 输入:matrix …...

中创算力:以知识产权转化运用促进高质量发展
创新是引领发展的第一动力,保护知识产权就是保护创新。为深入实施知识产权公共服务普惠工程,促进知识产权公共服务更好服务高水平科技,国家知识产权局发布关于全面提升知识产权公共服务效能的指导意见。 在政策落地过程中,如何精…...

C语言9~10 DAY(合集)
数组的概念 什么是数组 数组是相同类型,有序数据的集合。 数组的特征 数组中的数据被称为数组的元素,是同构的 数组中的元素存放在内存空间里 (char player_name[6]:申请在内存中开辟6块连续的基于char类型的变量空间) 衍生概念&#x…...

【Kubernetes】应用的部署(一):金丝雀部署
应用的部署(一):金丝雀部署 在项目迭代开发过程中,经常需要对应用进行上线部署。上线部署策略主要有 3 种:金丝雀部署、蓝绿部署 和 滚动部署。 金丝雀部署 也被叫作 灰度部署。金丝雀部署过程:先让一部分…...

1.面试准备篇
筛选简历 找实习用处不大 简历注意事项 注意职业技能和项目经历 职业技能 黄金位置 针对性 引导面试官提问 只写会的 不会的不能写 项目描述 主要设计… 展示指标 找练手项目 来源:Gitee 或者github 主要关注点:功能实现、常见问题、系统设计 面试过程 一面…...

Spring: try-catch 是否还会回滚
问题出现: try-catch 语句 依旧会抛出如下错误 org.springframework.transaction.TransactionSystemException: Could not commit JPA transaction; nested exception is javax.persistence.RollbackException: Transaction marked as rollbackOnlyat org.springf…...

spdlog日志库--基础介绍
文章目录 1. 简介1.1. spdlog代码特点1.2. 说明1.3. spdlog架构 2. spdlog的安装2.1. 使用包管理器安装2.2. 使用源码安装2.3. 仅使用头文件 3. 相关概念3.0 常用的头文件3.1. level_enum3.2. sink3.3. logger3.4 格式输出3.5 对齐方式3.6 截断3.7 字符串格式化fmt 4. 特性4.1.…...
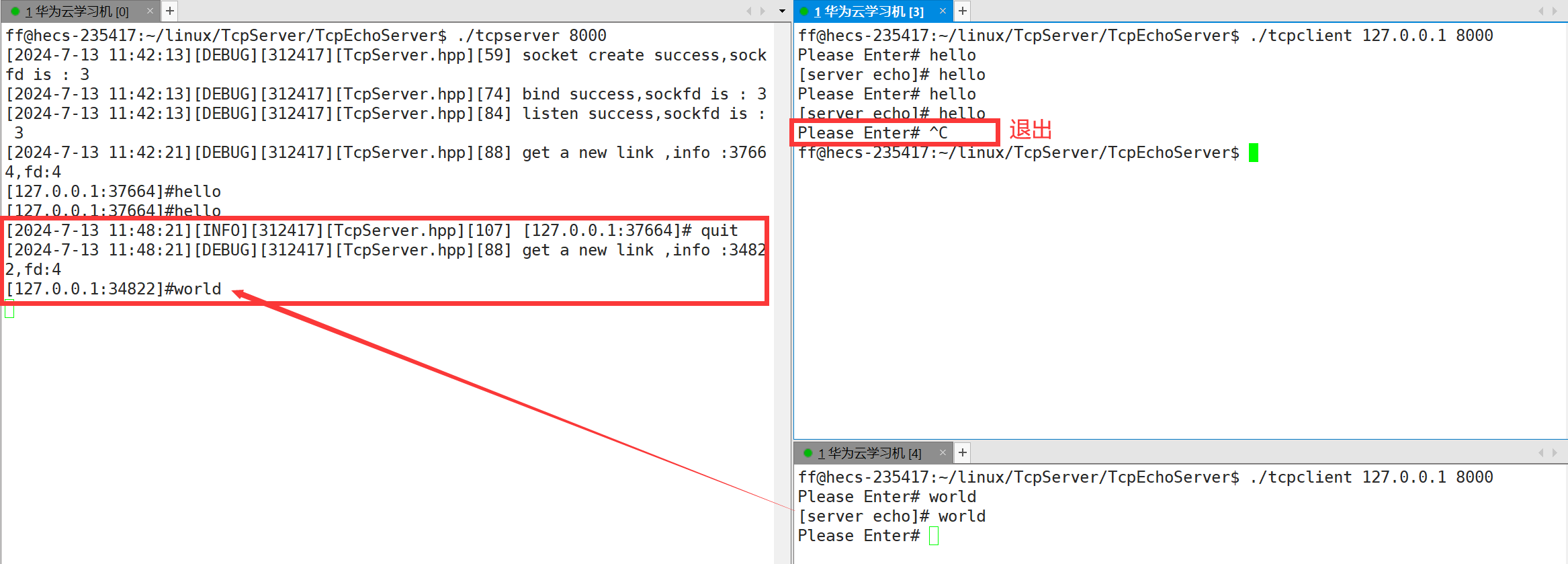
【网络】网络编程套接字(二)
网络编程套接字(二) 文章目录 1.单执行流的TCP网络程序1.1服务端创建套接字1.2服务端绑定1.3服务端监听1.4服务端获取链接1.5服务端处理请求1.6客户端创建套接字1.7客户端连接服务器1.8客户端发起请求 2.多进程版的TCP网络程序2.1单执行流的弊端2.2多进…...
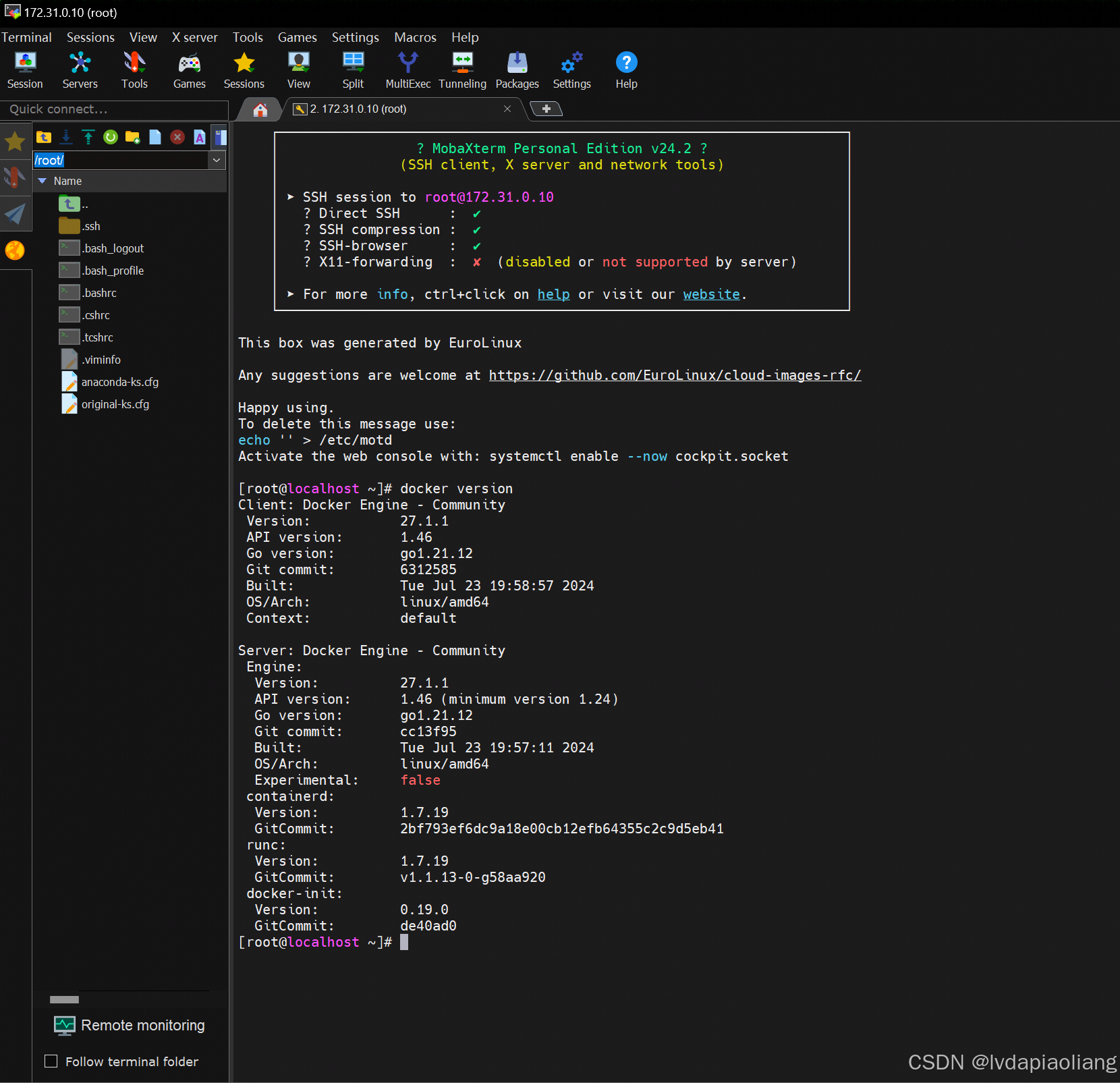
1.1、centos stream 9安装Kubernetes v1.30集群 环境说明
最近正在学习kubernetes,买了一套《Kubernetes权威指南 从Docker到Kubernetes实践全接触(第六版)》这本书讲得很好,上下两册,书中k8s的版本是V1.29,目前官网最新版本是v1.30。强烈建议大家买一套看看。 Kubernetes官网地址&#x…...

Redis3
目录 什么是缓存穿透?怎么解决? 什么是缓存雪崩?怎么解决? 如何保证数据库和缓存的数据一致性? 如何保证Redis服务高可用? 哨兵的作用 Redis虚拟槽分区有什么优点? 为什么Redis集群最大槽…...

Oracle数据巡检 - 设计巡检模板
设计巡检模板 明确巡检数据库等信息 包括数据库种类、版本、架构、数量等,例如 Oracle DG和Oracle RAC数据库巡检项肯定会有差异,Oracle 11g和12c版本巡检内容也会有所不同。 明确巡检项 这一块需要结合自身的运维经验,列出详尽的巡检项&…...

优盘未格式化数据恢复实战指南
在数字时代,优盘(USB闪存驱动器)作为便携存储媒介,承载着无数重要的文件与数据。然而,当您插入优盘准备访问资料时,却遭遇了“驱动器未被格式化”的提示,这无疑是一场突如其来的数据危机。本文将…...
)
【python基础】python基础习题练习(一)
文章目录 一. python语言简介二. python基本语法与常用函数三. python基本数据类型一.选择题二.编程题四. python组合数据类型一.选择题二.简答题三.编程题一. python语言简介 查看python是否安装成功的命令是:python -vPython IDE有:pyCharm、Spyder、Jupter NotebookPython…...

GESP 4级样题 ---> 绝对素数
这题需要判断一个数和它的反转后的数是否都为素数。 可以转成 string 后 reverse 一下。 AC CODE: #include <bits/stdc.h> using namespace std; typedef long long LL; bool isPrime(int x){if(x<2) return false;for(int i2;i*i<x;i){if(x%i0) re…...

大语言模型系列 - Transformer
1. 简介 1.1. 概述 大语言模型Transformer是一种由谷歌公司提出的基于注意力机制的神经网络模型,它在自然语言处理(NLP)领域取得了显著成就,并逐渐被应用于其他领域如语音识别、计算机视觉和强化学习等。 1.2. 学习资源 以下是一些学习大语言模型Transformer的资源地址…...

Java面试之操作系统
1、冯诺依曼模型 运算器、控制器、存储器、输入设备、输出设备 32位和64位CPU最主要区别是一次性能计算多少字节数据,如果计算的数额不超过 32 位数字的情况下,32 位和 64 位 CPU 之间没什么区别的,只有当计算超过 32 位数字的情况下&#…...
springboot船舶维保管理系统--论文源码调试讲解
第二章 相关技术 本次开发船舶维保管理系统使用的是Vue进行程序开发,船舶维保管理系统的数据信息选择MySQL数据库进行存放。 2.1 VUE介绍 Vue (读音 /vjuː/,类似于 view) 是一套用于构建用户界面的渐进式框架。与其它大型框架不同的是,Vue…...
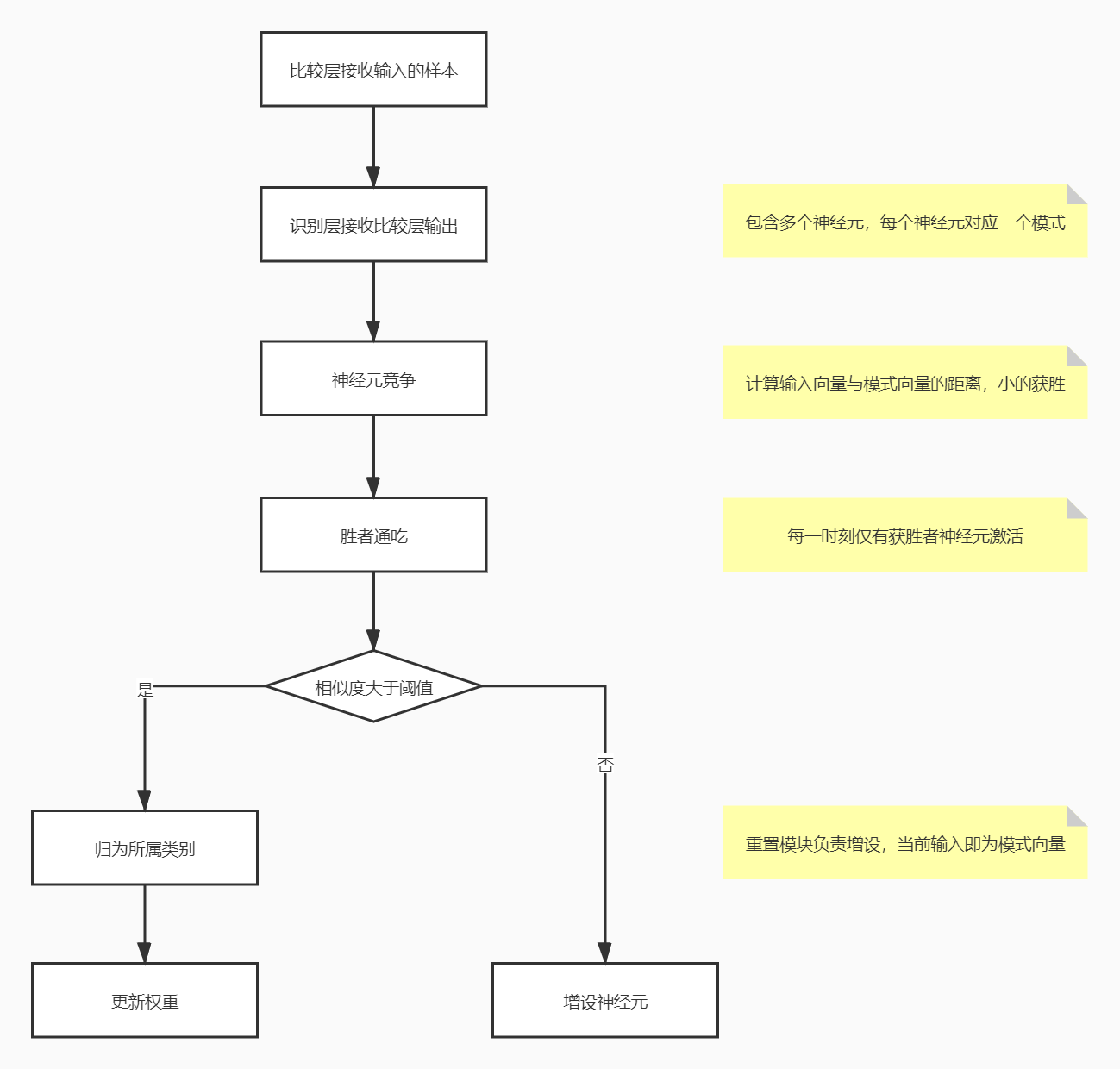
【机器学习西瓜书学习笔记——神经网络】
机器学习西瓜书学习笔记【第五章】 第五章 神经网络5.1神经元模型5.2 感知机与多层网络学习感知机学习率成本/损失函数梯度下降 5.3 BP神经网络(误差逆传播)5.4 全局最小与局部极小5.5 其他常见神经网络RBF网络RBF 与 BP 最重要的区别 ART网络 第五章 神…...

安装 electron 报错解决
1. 报错 大概率由镜像问题导致 2. 解决 2.1 打开 npm 配置 npm config edit 2.2 添加配置 registryhttps://registry.npmmirror.comelectron_mirrorhttps://cdn.npmmirror.com/binaries/electron/electron_builder_binaries_mirrorhttps://npmmirror.com/mirrors/electron…...

【Material-UI】Icon Button 组件详解
文章目录 一、基础用法1. 禁用状态 二、大小(Sizes)1. 小尺寸(Small)2. 大尺寸(Large) 三、颜色(Colors)1. 主题颜色2. 自定义颜色 四、高级用法和最佳实践1. 无障碍性(A…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...