174.地下城游戏——LeetCode
题目
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。

输入:dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出:7
解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。
解题思路
这个问题是一个典型的动态规划问题,我们需要找到从左上角到右下角的路径上,骑士所需的最小初始健康点数,使得在任何时候骑士的健康点数都不会降到0或以下。
动态规划的状态转移方程应该是这样的:
设 dp[i][j] 表示到达房间 (i, j) 时所需的最小生命值。由于骑士可以选择向下或向右移动,dp[i][j] 可以通过 dp[i+1][j](从上方房间来)或 dp[i][j+1](从左侧房间来)计算得出。我们需要考虑以下两种情况:
- 如果从上方房间
(i+1, j)来,骑士需要在当前房间(i, j)至少剩余dp[i+1][j] - dungeon[i+1][j]生命值。 - 如果从左侧房间
(i, j+1)来,骑士需要在当前房间(i, j)至少剩余dp[i][j+1] - dungeon[i][j+1]生命值。
我们需要取这两种情况中的较大者,因为骑士需要在进入房间前保证足够的生命值。然后,我们需要考虑当前房间 (i, j) 的效果 dungeon[i][j],如果 dungeon[i][j] 是负数,骑士将失去生命值。
因此,状态转移方程为:
解题过程
-
初始化
dp数组,其大小与dungeon相同。 -
设置右下角的
dp值,根据房间值决定初始健康点数。 -
从右下角开始向上和向左遍历
dungeon,填充dp数组。 -
对于每个格子
(i, j),计算从右边(i, j+1)和下面(i+1, j)到达的最小健康点数,并取较小者。 -
从计算结果中减去当前格子的值,确保结果至少为1(因为骑士不能有0或负的健康点数)。
-
循环结束后,
dp[0][0]就是所需的最小初始健康点数。
复杂度
-
时间复杂度:O(m×n)O(m×n),其中
m和n分别是dungeon的行数和列数。我们需要遍历整个dungeon。 -
空间复杂度:O(m×n)O(m×n),用于存储动态规划表
dp。如果只存储一行或一列的状态,可以优化到 O(min(m,n))O(min(m,n))。
Code
class Solution {public int calculateMinimumHP(int[][] dungeon) {final int m = dungeon.length, n = dungeon[0].length;int[][] dp = new int[m][n];// 初始化dp数组的右下角dp[m - 1][n - 1] = Math.max(1, 1 - dungeon[m - 1][n - 1]);// 从右下角开始向上和向左遍历for (int i = m - 2; i >= 0; i--) {dp[i][n - 1] = Math.max(1, dp[i + 1][n - 1] - dungeon[i][n - 1]);}for (int j = n - 2; j >= 0; j--) {dp[m - 1][j] = Math.max(1, dp[m - 1][j + 1] - dungeon[m - 1][j]);}// 动态规划填表for (int i = m - 2; i >= 0; i--) {for (int j = n - 2; j >= 0; j--) {// 取右边和下边的最小值,并减去当前房间的值dp[i][j] = Math.max(1, Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]);}}return dp[0][0];}
}相关文章:
174.地下城游戏——LeetCode
题目 恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。 骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻…...

登录相关功能的优化【JWT令牌+拦截器+跨域】
登录相关功能的优化 登录后显示当前登录用户el-dropdown: Element - The worlds most popular Vue UI framework <el-dropdown style"float: right; height: 60px; line-height: 60px"><span class"el-dropdown-link" style"color: white;…...

向日葵没有显示器会卡住
前言 有一台机器【ubuntu20】,用于远程开发,使用向日葵时候,如果不接显示器是会卡住的。。。 显示屏是有限的,所以现在解决一下这个问题。 卡在登录界面 双击启动 由于Ubuntu默认显示管理器是gdm,而向日葵使用的是l…...

【机器学习西瓜书学习笔记——聚类】
机器学习西瓜书学习笔记【第九章】 第九章 聚类9.1 聚类任务9.2 性能度量两类指标 9.3距离计算基本性质属性有序属性无序属性 混合距离加权距离 9.4 原型聚类K-MEANS聚类算法步骤优势劣势 学习向量量化高斯混合聚类步骤难点例子EM思想的体现小结 9.5 密度聚类9.6 层次聚类 第九…...

MATLAB(8)深度变化模型
一、前言 在MATLAB中模拟深度变化模型通常依赖于具体的应用场景,比如海洋深度、地下水深度、地形高度变化等。由于“深度变化”可以涉及多种物理过程和数学模型,我将提供一个简化的示例,该示例模拟了一个基于时间变化的深度变化模型ÿ…...

mp3格式转换器哪个好用?汇总七款音频格式转换方法(无损转换)
音乐已经成为我们生活中不可或缺的一部分。但是在播放的时候,可能会遇到音频格式不兼容的情况。特别是在一些下载站或音乐平台获取的音频,有些特殊格式在播放器上无法正常播放,一般这种情况我们需要借助mp3转换器解决。 mp3是一种常见的数字音…...

移行前的复盘:CodeCommit 的重要地位分析
前言 截至7月28日,关于AWS CodeCommit的现状如下: 现有账号的现有存储库可以继续使用CodeCommit,不受限制。之前未使用过CodeCommit的账号(或没有现有存储库的账号)无法创建新的存储库。 这并不意味着CodeCommit的服…...
)
Java中等题-括号生成(力扣)
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:["((()))","(()())","(())()","()(())","()()(…...

Flink 实时数仓(八)【DWS 层搭建(二)流量域、用户域、交易域搭建】
前言 今天的任务是完成流量域最后一个需求、用户域的两个需求以及交易域的部分需求; 1、流量域页面浏览各窗口汇总表 任务:从 Kafka 页面日志主题读取数据,统计当日的首页和商品详情页独立访客数。 注意:一般我们谈到访客&…...

gitlab-runner /var/run/docker.sock connect permission denied
usermod -aG docker gitlab-runner sudo service docker restart参考:https://gitlab.com/gitlab-org/gitlab-runner/-/issues/3492...

网络安全 - 应急响应检查表
前言 本项目旨在为应急响应提供全方位辅助,以便快速解决问题。结合自身经验和网络资料,形成检查清单,期待大家提供更多技巧,共同完善本项目。愿大家在应急之路一帆风顺。 图片皆来源于网络,如有侵权请联系删除。 一…...
)
AD常用PCB设计规则介绍 (详细版)
AD09常用PCB设计规则介绍 电气设计规则用来设置在电路板布线过程中所遵循的电气方面的规则,包括安全间距、短路、未布线网络和未连接引脚这四个方面的规则: (1)、安全间距规则(clearance) 该规则用于设定在PCB设计中࿰…...

mysql主从服务配置
主从MySQL服务器 [rootlocalhost ~]# yum -y install ntpdate [rootlocalhost ~]# ntpdate cn.ntp.org.cn [rootlocalhost ~]# yum -y install rsync [rootlocalhost ~]# vim mysql.sh #!/bin/bash yum list installed |grep libaio if [ $? ne 0 ]; then yum -y install…...
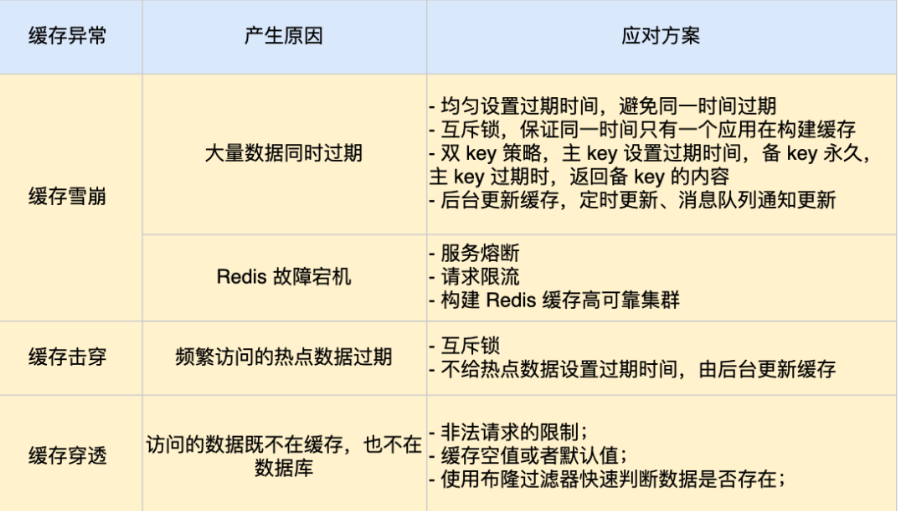
Redis基础总结、持久化、主从复制、哨兵模式、内存淘汰策略、缓存
文章目录 Redis 基础Redis 是什么,有哪些特点为什么要使用 Redis 而不仅仅依赖 MySQLRedis 是单线程吗Redis 单线程为什么还这么快 Redis 数据类型和数据结构五种基本数据结构及应用场景其他数据类型Redis 底层数据结构 Redis 持久化数据不丢失的实现AOF 日志RDB 快…...

Java与Python优劣势对比:具体例子与深入分析
在软件开发的世界里,Java和Python是两座不可忽视的高峰。它们各自拥有独特的优势和应用场景,为开发者提供了多样化的选择。本文将通过具体例子,深入分析Java和Python在不同方面的表现,以期为读者提供更为详尽的参考。 1. 语法简洁…...

C++内存泄漏介绍
C内存泄漏(Memory Leak)是指程序在运行过程中,动态分配的内存没有被适当地释放或回收,导致这部分内存始终被占用,无法再被程序或其他程序使用。这种情况通常发生在使用了new或malloc等函数动态分配内存后,忘…...
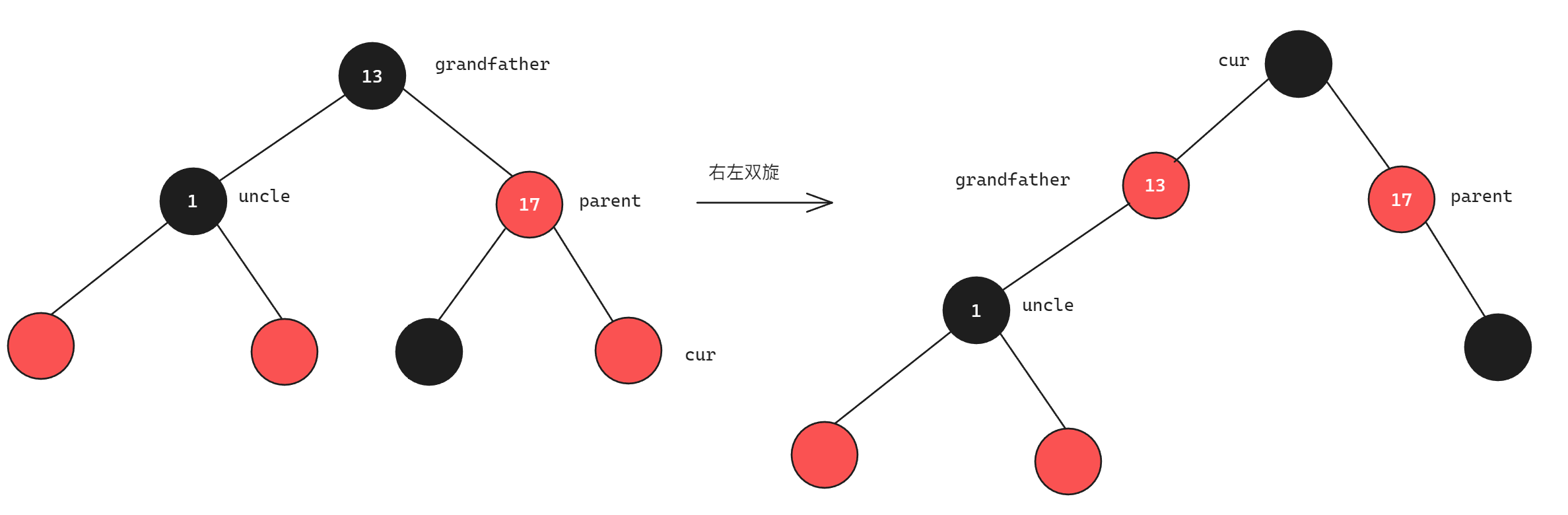
C++分析红黑树
目录 红黑树介绍 红黑树的性质与平衡控制关系 红黑树节点的插入 情况1:不需要调整 情况2:uncle节点为红色 情况3:uncle节点为黑色 总结与代码实现 红黑树的删除(待实现) 红黑树的效率 红黑树介绍 红黑树是第二种平衡二…...

mysql线上查询之前要性能调优
查询优化是数据库性能调优的关键方面,目的是减少查询的执行时间和资源消耗。以下是一些常见的查询优化技巧及其示例: 使用合适的索引 问题: 全表扫描导致查询缓慢优化: 为经常用于搜索条件的列添加索引示例: 假设有一…...

GPIO输出控制之LED闪烁、LED流水灯以及蜂鸣器应用案例
系列文章目录 STM32之GPIO(General Purpose Input/Output,通用型输入输出) 文章目录 系列文章目录前言一、LED和蜂鸣器简介1.1 LED1.2 蜂鸣器1.3 面包板 二、LED硬件电路2.1 低电平驱动电路2.2 高电平驱动电路 三、蜂鸣器硬件电路3.1 PNP型三…...

体系结构论文导读(三十四):Design of Reliable DNN Accelerator with Un-reliable ReRAM
文章核心 这篇文章主要讨论了一种在不可靠的ReRAM(阻变存储器)设备上设计可靠的深度神经网络(DNN)加速器的方法。文章提出了两种关键技术来解决ReRAM固有的不可靠性问题:动态定点(DFP)数据表示…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...

性能优化中,多面体模型基本原理
1)多面体编译技术是一种基于多面体模型的程序分析和优化技术,它将程序 中的语句实例、访问关系、依赖关系和调度等信息映射到多维空间中的几何对 象,通过对这些几何对象进行几何操作和线性代数计算来进行程序的分析和优 化。 其中࿰…...

Unity-ECS详解
今天我们来了解Unity最先进的技术——ECS架构(EntityComponentSystem)。 Unity官方下有源码,我们下载源码后来学习。 ECS 与OOP(Object-Oriented Programming)对应,ECS是一种完全不同的编程范式与数据架构…...
