洛谷练习(8.4/8.5)
题目
- P2036 PERKET
- 题目描述
- 思路
- 代码
- P3799 小 Y 拼木棒
- 题目描述
- 思路
- 代码
- P1010 幂次方
- 题目描述
- 思路
- 代码
- P1498 南蛮图腾
- 题目描述
- 思路
- 代码
- P1928 外星密码
- 题目描述
- 思路
- 代码
P2036 PERKET
题目描述
比较苦度和酸度的最小差值
思路
搜索最小差值
代码
void dfs(int sd,int kd,int cnt)
{if(cnt==n){int sum=abs(sd-kd);if(sum<summ&&kd!=0) summ=sum;//定义summ为一个特别大的数不断更新return ;}cnt++;dfs(sd*s[cnt],kd+b[cnt],cnt);//加上这个数dfs(sd,kd,cnt);//不加当前数
}
signed main()
{long long suma=1,sumb=0,sum=0;cin>>n;for(int i=1;i<=n;i++){cin>>s[i]>>b[i];dfs(1,0,0);} cout<<summ;return 0;
}
P3799 小 Y 拼木棒
题目描述
选取4根木棒摆成正三角形
思路
计算不同长度木棍的数量,排列组合
代码
int main()
{long long n,count[50000]={0},a,sum=0,ans=0;cin >> n;for (int i = 1; i <= n; i++){cin >> a;count[a]++;//计数} for (int i = 1; i <= 2500; i++) //因为最大值5000,因为两个数相加所以不超2500for (int j = i ; j <= 5000-i; j++){int c1=count[i];int c2=count[j];//两种短棍的数量int c3=count[i+j];//长棍的数量if(c3>=2){if(i==j&&c1>=2)//正好i等于j{sum=c1*(c1-1)/2*c3*(c3-1)/2%1000000007;//就是从c1个数中选两个,再从c3个数中选两个ans+=sum;}if(i!=j&&c1>=1&&c2>=1){sum=c1*c2*c3*(c3-1)/2%1000000007;//从c1,c2中各选一个,在c3中选两个ans+=sum;}}} cout << ans%1000000007;//数值太大要取模return 0;
}
P1010 幂次方
题目描述
把一个数用全是2或者0,表示出来
思路
递归/分治,先减去距离这个数最近的2的i的数,逐层递减
代码
void solve(int x)
{ for(int i=14;i>=0;i--)if(pow(2,i)<=x){if(i==1) cout<<"2";else if(i==0) cout<<"2(0)";else{cout<<"2(";solve(i);cout<<")"; } x-=pow(2,i);if(x!=0) cout<<"+";}
}
P1498 南蛮图腾
题目描述
画三角形的图腾
思路
分治,就是对三角形的复制移动(代码注释会详细一点)
代码
char a[2050][2050];
void sol(int x,int y,int n)//x表示纵向,y表示横向
{int ds=pow(2,n);//偏移距离if(n==1){a[x][y+1]='/';a[x+1][y]='/';a[x][y+2]='\\';a[x+1][y+3]='\\';a[x+1][y+1]='_';a[x+1][y+2]='_';//就是一个三角形的return ;}//下面是对,n为2 的时候有三个小三角形的,与一个三角形的位置移动对比sol(x,y+ds/2,n-1);//第一个sol(x+ds/2,y,n-1);//第二个sol(x+ds/2,y+ds,n-1);//第三个
}
int main()
{int n;cin>>n;int ds=pow(2,n);memset(a,' ',sizeof(a));sol(0,0,n);for(int i=0;i<ds;i++){for(int j=0;j<ds*2;j++)//因为横向距离是纵向的2倍cout<<a[i][j];cout<<'\n';}return 0;
}
P1928 外星密码
题目描述
就是把折叠的字符串展开
思路
递归,遇到’['后面数字是几就循环接到后面几次,遇到‘]’
返回
代码
string unfold() //定义string类型,便于直接接后面
{ int n;string s="",sj;char c;while(cin>>c){if(c=='['){cin>>n;sj=unfold();while(n--)s+=sj;把需要展开的接后面}else{if(c==']') return s;else s+=c;} } return s;
}
int main()
{cout<<unfold();return 0;
}
相关文章:
)
洛谷练习(8.4/8.5)
题目 P2036 PERKET题目描述思路代码 P3799 小 Y 拼木棒题目描述思路代码 P1010 幂次方题目描述思路代码 P1498 南蛮图腾题目描述思路代码 P1928 外星密码题目描述思路代码 P2036 PERKET 题目描述 比较苦度和酸度的最小差值 思路 搜索最小差值 代码 void dfs(int sd,int k…...
1)
DLMS/COSEM中的信息安全:加密算法(下)1
4.公钥算法 4.1概述 一般来说,公钥密码系统使用难以解决的问题作为算法的基础。RSA算法基于非常大的整数的素因子分解。椭圆曲线密码学(ECC)是基于求解椭圆曲线离散对数问题(ECDLP)的难度。与RSA相比,ECC提供了相似的安全级别,但密钥大小明显减少。ECC特别适用于嵌入式…...

ES6中的Promise、async、await,超详细讲解!
Promise是es6引入的异步编程新解决方案,Promise实例和原型上有reject、resolve、all、then、catch、finally等多个方法,语法上promise就是一个构造函数,用来封装异步操作并可以获取其成功或失败的结果,本篇文章主要介绍了ES6中的P…...

Modbus poll和Modbus Mbslave的使用
读取Modbus Mbslave中的数据 首先创建COM1和COM2端口 然后 using System.IO.Ports; namespace 通信 {internal class Program{static void Main(string[] args){Console.WriteLine("Hello, World!");SerialPort serialPort new SerialPort("COM1",960…...

树莓集团的全球化征程:数字媒体产业的本土与国际布局
在全球数字化转型的浪潮中,树莓集团正稳步推进数字媒体产业从本土到国际的全球化布局。在数字媒体产业这一新兴且充满活力的领域中,树莓集团不仅在国内市场树立了标杆,更以其独特的全球化战略布局,引领着行业的未来趋势。 本土深耕…...

LeetCode面试150——274H指数
题目难度:中等 默认优化目标:最小化平均时间复杂度。 Python默认为Python3。 目录 1 题目描述 2 题目解析 3 算法原理及代码实现 3.1 排序 3.2 排序时间优化(计数排序) 3.3 二分查找 参考文献 1 题目描述 给你一个整数数组 citations …...
【Linux】Linux重定向指南:探索输出重定向与追加重定向的奥秘!
欢迎来到 CILMY23 的博客 🏆本篇主题为:Linux重定向指南:探索输出重定向与追加重定向的奥秘! 🏆个人主页:CILMY23-CSDN博客 🏆系列专栏:Python | C | C语言 | 数据结构与算法 | 贪…...
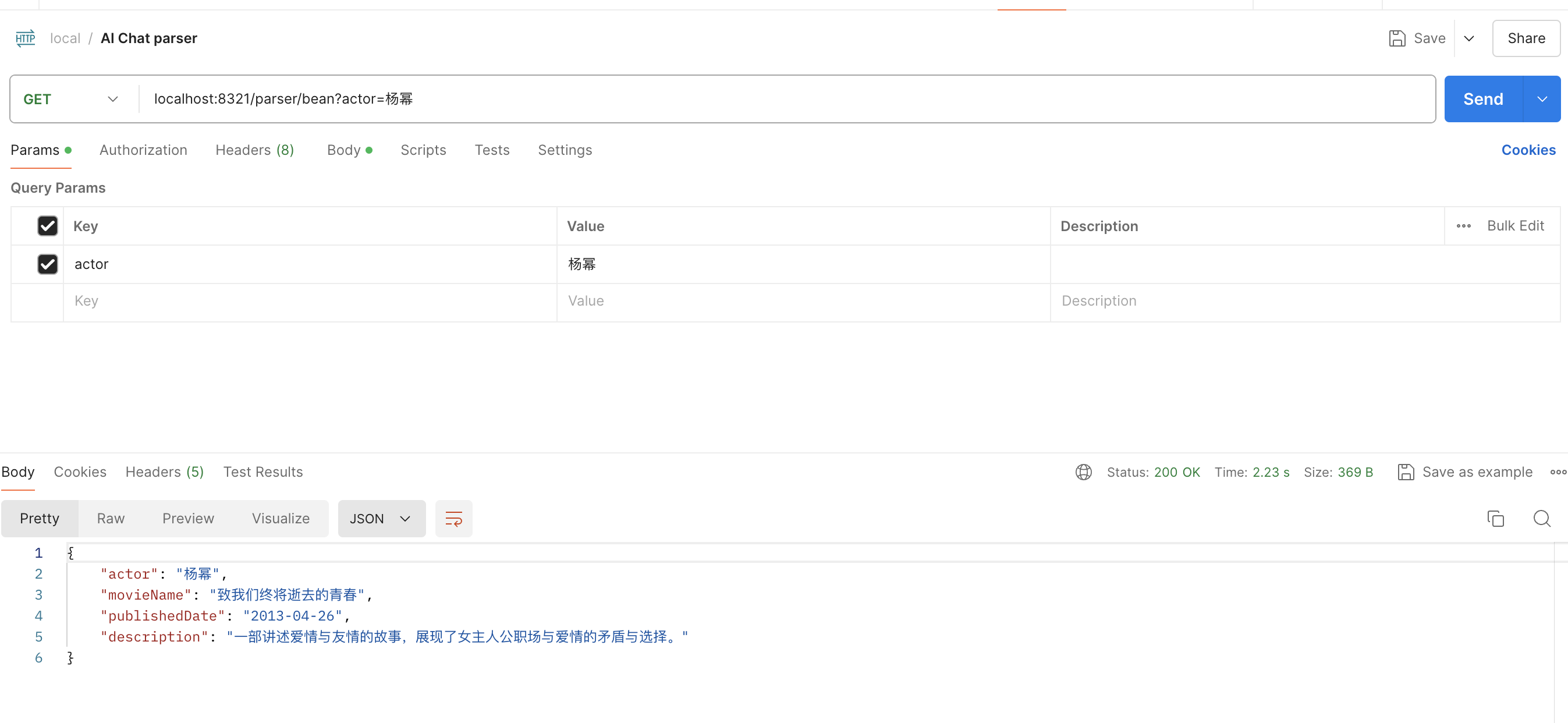
Spring AI -快速开发ChatGPT应用
Spring AI介绍 Spring AI是AI工程师的一个应用框架,它提供了一个友好的API和开发AI应用的抽象,旨在简化AI应用的开发工序,例如开发一款基于ChatGPT的对话、图片、音频等应用程序。 Spring AI已经集成了OpenAI的API,因此我们不需…...

Modern C++ 智能指针
Why? 原始指针存在缺陷,不符合现代编程语言的需要。 原始指针的缺陷: 指针指向一片内存,使用者无法得知到底是指向了什么,是数组还是对象?使用完指针是否需要销毁?什么时候销毁?如…...

Python的100道经典练习题,每日一练,必成大神!!!
Python的100道经典练习题是一个广泛而深入的学习资源,可以帮助Python初学者和进阶者巩固和提升编程技能 完整的100多道练习题可在下面图片免沸获取哦~ 整理了100道Python的题目,如果你是一位初学者,这一百多道题可以 帮助你轻松的使用Python…...

代码回滚命令
定位到当前分支 git branch回滚到指定的commit git reset --hard 85da0cb8322accad143cpush到远程分支 git push --force...

[ASIS 2019]Unicorn shop1
打开题目 随便输入信息看一下 操作失败,只让输入一个字符 不妨抓包看一下,信息,发现 从中可以发现源代码是如何处理price的 使用的是unicodedata.numeric() 但我们查看页面源码时,看到源码处理方式是utf-8 所以,前…...

LangChain与泛型编程:探索代码生成的新维度
LangChain与泛型编程:探索代码生成的新维度 在软件开发领域,泛型编程是一种允许创建可重用组件的技术,这些组件可以在多种数据类型上工作的编程范式。LangChain作为一个假设的编程辅助工具,如果存在,它可能会支持泛型…...

day25
一、进程间通信(IPC) 1.1 进程间通信的引入 1> 对于多个线程之间通信,我们可以使用临界资源来完成,通过一个线程任务对临界资源进行修改,另一个线程也可以使用已经修改过的临界资源,但是要注意使用…...

红黑树的概念和模拟实现[C++]
文章目录 红黑树的概念一、红黑树的性质红黑树原理二、红黑树的优势和比较 红黑树的模拟实现构建红黑树的数据结构定义节点的基本结构和初始化方式插入新节点插入新节点的颜色调整颜色和结构以满足红黑树性质 红黑树的应用场景 红黑树的概念 一、红黑树的性质 红黑树是一种自平…...

网络安全应急响应概述
前言 在网络安全领域,有一句广为人知的话:“没有绝对的安全”。这意味着任何系统都有可能被攻破。安全攻击的发生并不可怕,可怕的是从头到尾都毫无察觉。当系统遭遇攻击时,企业的安全人员需要立即进行应急响应,以将影响…...
【C++】链表操作技巧综合:重排链表(带你理顺链表的做题思路)
1.题目 2.算法思路 这是一道关于链表的综合题,一共涉及到三个步骤,其中每个步骤单拎出来就可以当一道单独的题目。所以需要大家对链表的操作十分熟悉,否则可能需要大量的时间做这道题目,而且还要很多的bug。 第一个步骤…...

行为型设计模式2:观察者/职责链/中介者/访问者
设计模式:观察者/职责链/中介者/访问者 (qq.com)...

叛逆,批判
1、对以往说法的批判之一(第一次这么公开批判是2004-2005年): 这部英文版的《数学百科全书》似乎是从俄语版翻译过来的?我查了三本引用的图书文献,都没有关于“nonsingular”和“singular”的类似下面的说法ÿ…...

Linux 命令,mkdir说明与使用
1:mkdir命令功用: 用于创建一个或多个目录,创建目录,必须在父目录中写上权限。 新目录的默认模式为0777,可以由系统或用的umask来修改。 2:命令构件: mkdir [options] directories 3:参数选项: -m&#x…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
