selfAttention 中的dk到底是什么
在Self-Attention机制中,为什么需要对 Q K T QK^T QKT 的结果进行缩放,除以 d k \sqrt{d_k} dk。以下是详细解释:
缩放的原因
除以 d k \sqrt{d_k} dk 的原因有两个:
- 防止输入过大:如果不缩放, Q K T QK^T QKT的值可能会非常大,这会导致Softmax的值非常小,接近于0,从而造成梯度消失问题。
- 归一化:缩放使得 Q ⋅ K Q\cdot K Q⋅K 的结果满足均值为0,方差为1的分布,类似于归一化的效果。
数学推导
假设 Q Q Q和 K K K中的元素是从均值为0,方差为1的独立同分布随机变量。设 X = q i X = q_i X=qi和 Y = k i Y = k_i Y=ki,则:
- E ( X ) = E ( Y ) = 0 E(X) = E(Y) = 0 E(X)=E(Y)=0
- D ( X Y ) = E ( X 2 ) E ( Y 2 ) − [ E ( X ) E ( Y ) ] 2 = 1 ⋅ 1 − 0 = 1 D(XY) = E(X^2)E(Y^2) - [E(X)E(Y)]^2 = 1 \cdot 1 - 0 = 1 D(XY)=E(X2)E(Y2)−[E(X)E(Y)]2=1⋅1−0=1
因此, D ( ∑ i = 1 d k q i k i ) = d k D\left(\sum_{i=1}^{d_k} q_i k_i\right) = d_k D(∑i=1dkqiki)=dk。
对 Q K T QK^T QKT 的缩放:
D ( Q K T d k ) = 1 d k D ( ∑ i = 1 d k q i k i ) = 1 d k ⋅ d k = 1 D\left(\frac{QK^T}{\sqrt{d_k}}\right) = \frac{1}{d_k} D\left(\sum_{i=1}^{d_k} q_i k_i\right) = \frac{1}{d_k} \cdot d_k = 1 D(dkQKT)=dk1D(∑i=1dkqiki)=dk1⋅dk=1
好的,让我们通过一个具体的例子来说明 (d_k) 的作用以及为什么要除以 (\sqrt{d_k})。
假设我们有一个查询向量 q \mathbf{q} q 和一个键向量 k \mathbf{k} k,它们的维度 d k = 4 d_k = 4 dk=4。这些向量的元素是均值为0、方差为1的独立同分布随机变量。我们具体来看下这两个向量的点积结果以及缩放后的结果。
假设:
q = [ 1.2 , − 0.5 , 0.3 , 0.8 ] \mathbf{q} = [1.2, -0.5, 0.3, 0.8] q=[1.2,−0.5,0.3,0.8]
k = [ 0.6 , − 0.1 , − 1.5 , 0.7 ] \mathbf{k} = [0.6, -0.1, -1.5, 0.7] k=[0.6,−0.1,−1.5,0.7]
计算点积:
q ⋅ k = 1.2 × 0.6 + ( − 0.5 ) × ( − 0.1 ) + 0.3 × ( − 1.5 ) + 0.8 × 0.7 \mathbf{q} \cdot \mathbf{k} = 1.2 \times 0.6 + (-0.5) \times (-0.1) + 0.3 \times (-1.5) + 0.8 \times 0.7 q⋅k=1.2×0.6+(−0.5)×(−0.1)+0.3×(−1.5)+0.8×0.7
= 0.72 + 0.05 − 0.45 + 0.56 = 0.72 + 0.05 - 0.45 + 0.56 =0.72+0.05−0.45+0.56
= 0.88 = 0.88 =0.88
不进行缩放时,这个点积结果直接用于Softmax计算。但是,当 (d_k) 很大时,这个值可能会非常大,导致Softmax输出非常尖锐。为了避免这种情况,我们将点积结果除以 (\sqrt{d_k}) 来进行缩放。
在本例中, d k = 4 d_k = 4 dk=4,因此 d k = 2 \sqrt{d_k} = 2 dk=2。
缩放后的点积结果:
q ⋅ k d k = 0.88 2 = 0.44 \frac{\mathbf{q} \cdot \mathbf{k}}{\sqrt{d_k}} = \frac{0.88}{2} = 0.44 dkq⋅k=20.88=0.44
现在我们来比较一下经过Softmax之前的值和经过缩放后的值在Softmax函数中的效果:
假设有另外两个查询向量和键向量的点积结果分别为2.0和0.5,计算Softmax之前和之后的值。
不缩放时的点积结果:
未缩放的点积值 = [ 0.88 , 2.0 , 0.5 ] \text{未缩放的点积值} = [0.88, 2.0, 0.5] 未缩放的点积值=[0.88,2.0,0.5]
Softmax计算:
Softmax ( 0.88 , 2.0 , 0.5 ) = [ e 0.88 e 0.88 + e 2.0 + e 0.5 , e 2.0 e 0.88 + e 2.0 + e 0.5 , e 0.5 e 0.88 + e 2.0 + e 0.5 ] \text{Softmax}(0.88, 2.0, 0.5) = \left[ \frac{e^{0.88}}{e^{0.88} + e^{2.0} + e^{0.5}}, \frac{e^{2.0}}{e^{0.88} + e^{2.0} + e^{0.5}}, \frac{e^{0.5}}{e^{0.88} + e^{2.0} + e^{0.5}} \right] Softmax(0.88,2.0,0.5)=[e0.88+e2.0+e0.5e0.88,e0.88+e2.0+e0.5e2.0,e0.88+e2.0+e0.5e0.5]
≈ [ 0.184 , 0.643 , 0.173 ] \approx [0.184, 0.643, 0.173] ≈[0.184,0.643,0.173]
缩放后的点积结果:
缩放的点积值 = [ 0.44 , 1.0 , 0.25 ] \text{缩放的点积值} = [0.44, 1.0, 0.25] 缩放的点积值=[0.44,1.0,0.25]
Softmax计算:
Softmax ( 0.44 , 1.0 , 0.25 ) = [ e 0.44 e 0.44 + e 1.0 + e 0.25 , e 1.0 e 0.44 + e 1.0 + e 0.25 , e 0.25 e 0.44 + e 1.0 + e 0.25 ] \text{Softmax}(0.44, 1.0, 0.25) = \left[ \frac{e^{0.44}}{e^{0.44} + e^{1.0} + e^{0.25}}, \frac{e^{1.0}}{e^{0.44} + e^{1.0} + e^{0.25}}, \frac{e^{0.25}}{e^{0.44} + e^{1.0} + e^{0.25}} \right] Softmax(0.44,1.0,0.25)=[e0.44+e1.0+e0.25e0.44,e0.44+e1.0+e0.25e1.0,e0.44+e1.0+e0.25e0.25]
≈ [ 0.272 , 0.459 , 0.269 ] \approx [0.272, 0.459, 0.269] ≈[0.272,0.459,0.269]
可以看到,经过缩放后,Softmax的输出分布更加平滑,不再像未缩放前那样有较大的差异,这有助于梯度的稳定性和模型的训练效果。
通过这个例子,我们可以清楚地看到为什么在自注意力机制中对点积结果进行缩放是必要的,这样可以防止数值过大导致的问题,并且让Softmax的输出更为合理。
结论
通过上述推导,我们可以看到:
- 对 (QK^T) 进行缩放,使其满足均值为0,方差为1的分布。
- 这样处理后的值更加稳定,输入到Softmax函数后可以避免梯度消失问题。
综合解释
- 为什么要缩放:缩放可以防止输入到Softmax的值过大,导致梯度消失,同时使得分布更稳定。
- 缩放因子 d k \sqrt{d_k} dk:因为键向量 K K K 的维度为 d k d_k dk,在计算点积时需要对结果进行缩放,使其方差为1,保持稳定性。
通过对这些细节的处理,Self-Attention机制能够在训练和推理过程中保持数值稳定性和计算效率。
相关文章:

selfAttention 中的dk到底是什么
在Self-Attention机制中,为什么需要对 Q K T QK^T QKT 的结果进行缩放,除以 d k \sqrt{d_k} dk 。以下是详细解释: 缩放的原因 除以 d k \sqrt{d_k} dk 的原因有两个: 防止输入过大:如果不缩放…...

安装MongoDB UI客户端工具:mongodb-compass-1.40.2-win32-x64.msi
文章目录 1、安装 mongodb-compass-1.40.2-win32-x64.msi2、安装后配置链接地址: 1、安装 mongodb-compass-1.40.2-win32-x64.msi 2、安装后配置链接地址:...
一行命令搞定内网穿透
一行命令搞定内网穿透 一款开源免费的内网穿透工具:localtunnel ,基于 nodejs 实现,无需修改 DNS 和防火墙设置,方便快捷的将内网服务暴露到外网,为开发人员、测试人员以及需要分享本地项目的人提供实时的公网访问方式…...

C语言——扫雷游戏
扫雷游戏通常是一个由方格组成的区域内进行的,其中随机分布着一定数量的地雷 。玩家的目标是通过点击方格来标记出所有地雷的位置,同时避免自己点到地雷而导致游戏失败。游戏开始时,玩家通常只能看到一部分方格,而其余的方格则需要…...

【LLM】-16-评估LLM-与标准答案的差距
目录 1、评估回答是否正确 1.1、util_zh 1.2、eval_zh 1.3、评估 2、评估生成答案与标准答案的差距 2.1、eval_zh2 2.2、评估 即使没有提供的理想答案,只要能制定一个评估标准,就可以使用一个 LLM 来评估另一个 LLM 的输出。 如果可以提供理想答…...

WeNet 2.0:更高效的端到端语音识别工具包
WeNet 2.0:更高效的端到端语音识别工具包 原文链接:[2203.15455] WeNet 2.0: More Productive End-to-End Speech Recognition Toolkit (arxiv.org) 1.摘要 WeNet是一个开源的端到端语音识别工具包,WeNet 2.0在此基础上进行了四项主要更新,…...

阿里大模型调用 = 》通义千问大语言模型
背景:简单的通过API或者SDK在线调用阿里云大模型(基于百炼平台),基于在线知识库 参考地址:安装阿里云百炼SDK_大模型服务平台百炼(Model Studio)-阿里云帮助中心 (aliyun.com) 1、获取API-KEY 当您通过API/SDK调用大模…...

idea使用free流程,2024idea免费使用
1.先到官网下载,这里选择win系统的,点击下图的.exe https://www.jetbrains.com/idea/download/?sectionwindows 2.下载好后基本上就是一直点击“下一步”到直到安装好,安装好后先打开软件后关闭退出 3.下载配配套资料 链接: https://pan.ba…...

算法_链表专题---持续更新
文章目录 前言两数相加题目要求题目解析代码如下 两两交换链表中的结点题目要求题目解析代码如下 重排链表题目要求题目解析代码如下 合并K个升序链表题目要求题目解析 K个一组翻转链表题目要求题目解析代码如下 前言 本文将记录leetcode链表算法题解,包含题目有&a…...

在Windows MFC\C++编程中,如何使用OnCopyData函数
在C中,OnCopyData 函数通常不是标准C库的一部分,而是与特定的图形用户界面(GUI)框架相关联,如Microsoft Foundation Classes (MFC) 或 Windows API 编程。在MFC应用程序中,OnCopyData 是用于处理来自其他应…...

【Qt】项目代码
main.cpp文件 argc:命令行参数个数。*argv[ ]:每一个命令行参数的内容。main的形参就是命令行参数。QApplication a(argc, argv) 编写一个Qt的图形化界面程序,一定需要QApplication对象。 widget w; 在创建项目的时候,勾选widg…...
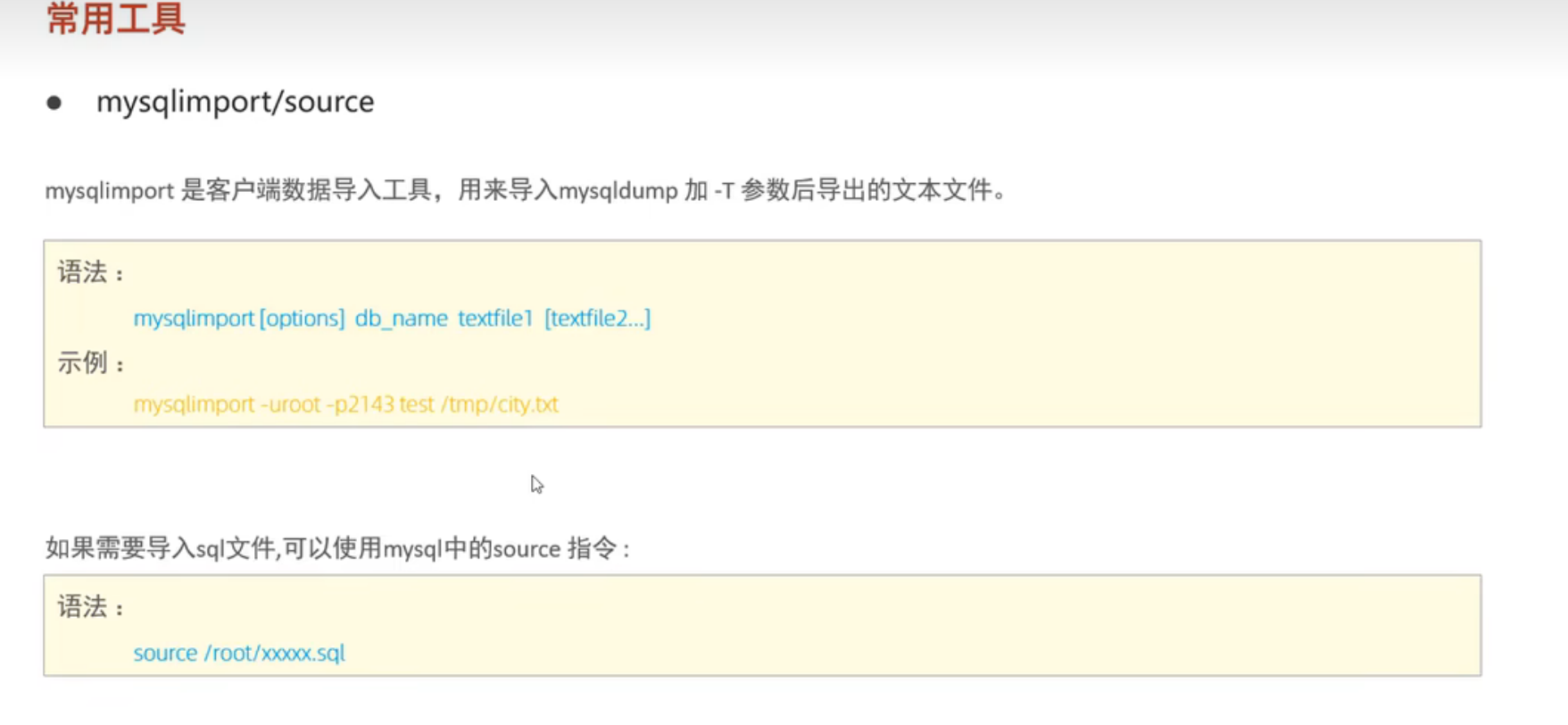
MySQL中常用工具
MySQL自带的系统数据库 常用工具 MySQL mysqladmin mysqlbinlog mysqldump mysqlimport/source mysqlimport只能导入文本文件,不能导入sql文件...
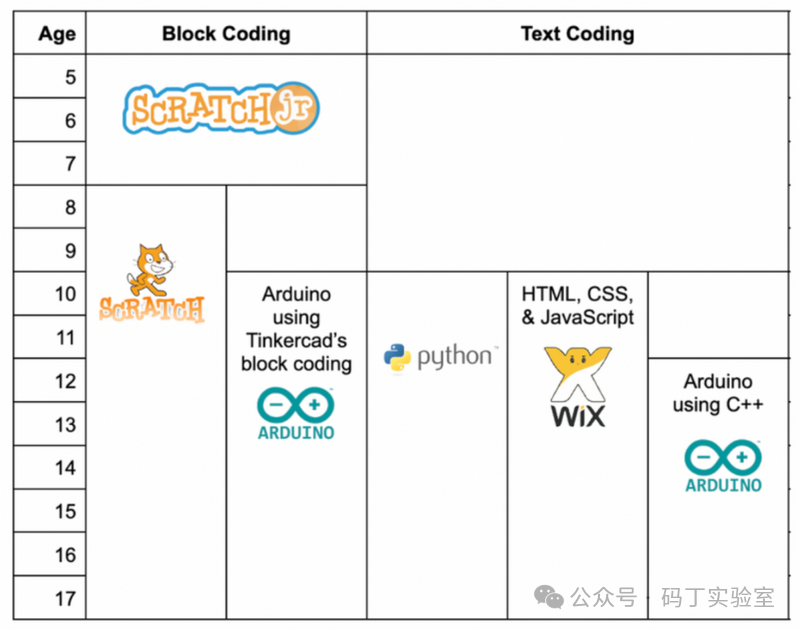
关于儿童编程语言
青少年通常会通过Scratch或Python开始学习编程。在这两种语言中,代码的编写(或者在Scratch中是构建)方式类似于英语,这使得初学者更容易学习。Scratch的一个重要卖点是对视觉和运动感知学习者非常友好。这些代码块按颜色编码&…...

[io]进程间通信 -信号函数 —信号处理过程
sighandler_t signal(int signum, sighandler_t handler); 功能: 信号处理函数 参数: signum:要处理的信号 handler:信号处理方式 SIG_IGN:忽略信号 SIG_DFL:执行默认操作 handler:捕捉信 …...

RoboDK的插件
目录 collision-free-planner: opc-ua: collision-free-planner: RoboDK 的无碰撞规划器插件使用概率路线图 (PRM) 自动在机器人工作空间内创建无碰撞路径。 有关无碰撞规划器的更多信息,请访问我们的 文档。 生成参数无碰撞…...

List<HashMap<String, Object>>排序
如果列表中的元素类型是List<HashMap<String, Object>>,排序时需要考虑到value可能是任意类型的对象。在这种情况下,你可以针对具体的类型进行比较,或者使用Comparable接口来确保对象可以被正确比较。 示例代码 假设我们想要根据…...

【大数据】探索大数据基础知识:定义、特征与生态系统
欢迎来到我的博客,很高兴能够在这里和您见面!欢迎订阅相关专栏: 工💗重💗hao💗:野老杂谈 ⭐️ 全网最全IT互联网公司面试宝典:收集整理全网各大IT互联网公司技术、项目、HR面试真题.…...

营销材料翻译质量对销售渠道的影响
在当今的全球市场中,与不同受众进行有效沟通的能力对于企业的成功至关重要。营销材料的高质量翻译在通过销售渠道塑造客户旅程方面发挥着重要作用,影响着知名度、参与度、转化率和保留率。方法如下: 提高品牌知名度 在销售渠道的顶端&#x…...

centos7.9安装k8s 1.3
centos7.9安装k8s 1.3 k8s环境规划:初始化修改网卡配置两台服务器都执行 配置阿里yum源 安装containerd服务安装初始化k8s需要的软件包kubeadm初始化k8s集群 扩容k8s集群-添加第一个工作节点安装kubernetes网络组件-Calico测试在k8s创建pod是否可以正常访问网络和co…...

【第七节】python多线程及网络编程
目录 一、python多线程 1.1 多线程的作用 1.2 python中的 threading 模块 1.3 线程锁 二、python网络编程 2.1 通过socket访问网络 2.2 python2.x中的编码问题 2.3 python3的编码问题 一、python多线程 1.1 多线程的作用 多线程技术在计算机编程中扮演着重要的角色&a…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
