【力扣】4.寻找两个正序数组的中位数
题目描述
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2] 输出:2.00000 解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4] 输出:2.50000 解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
AC代码
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {double ans;vector<double> num(2002);int m = nums1.size(), n = nums2.size(), m1 = 0, n1 = 0;int len = m + n;for (int i = 0; i <= len / 2; i++) {if (n1 == n) {num[i] = nums1[m1];m1++;}else if (m1 == m) {num[i] = nums2[n1];n1++;}else{num[i] = (nums1[m1] >= nums2[n1]) ? nums2[n1] : nums1[m1];if (nums1[m1] >= nums2[n1]) n1++;else m1++;}if ((m1 + n1) > (len / 2 + 1)) break;}if (len % 2) ans = num[len/2];else ans = (num[len/2-1] + num[len/2]) / 2.0;return ans;}
};相关文章:

【力扣】4.寻找两个正序数组的中位数
题目描述 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 算法的时间复杂度应该为 O(log (mn)) 。 示例 1: 输入:nums1 [1,3], nums2 [2] 输出:2.0…...

【C++】初识面向对象:类与对象详解
C语法相关知识点可以通过点击以下链接进行学习一起加油!命名空间缺省参数与函数重载C相关特性 本章将介绍C中一个重要的概念——类。通过类,我们可以类中定义成员变量和成员函数,实现模块化封装,从而构建更加抽象和复杂的工程。 &…...
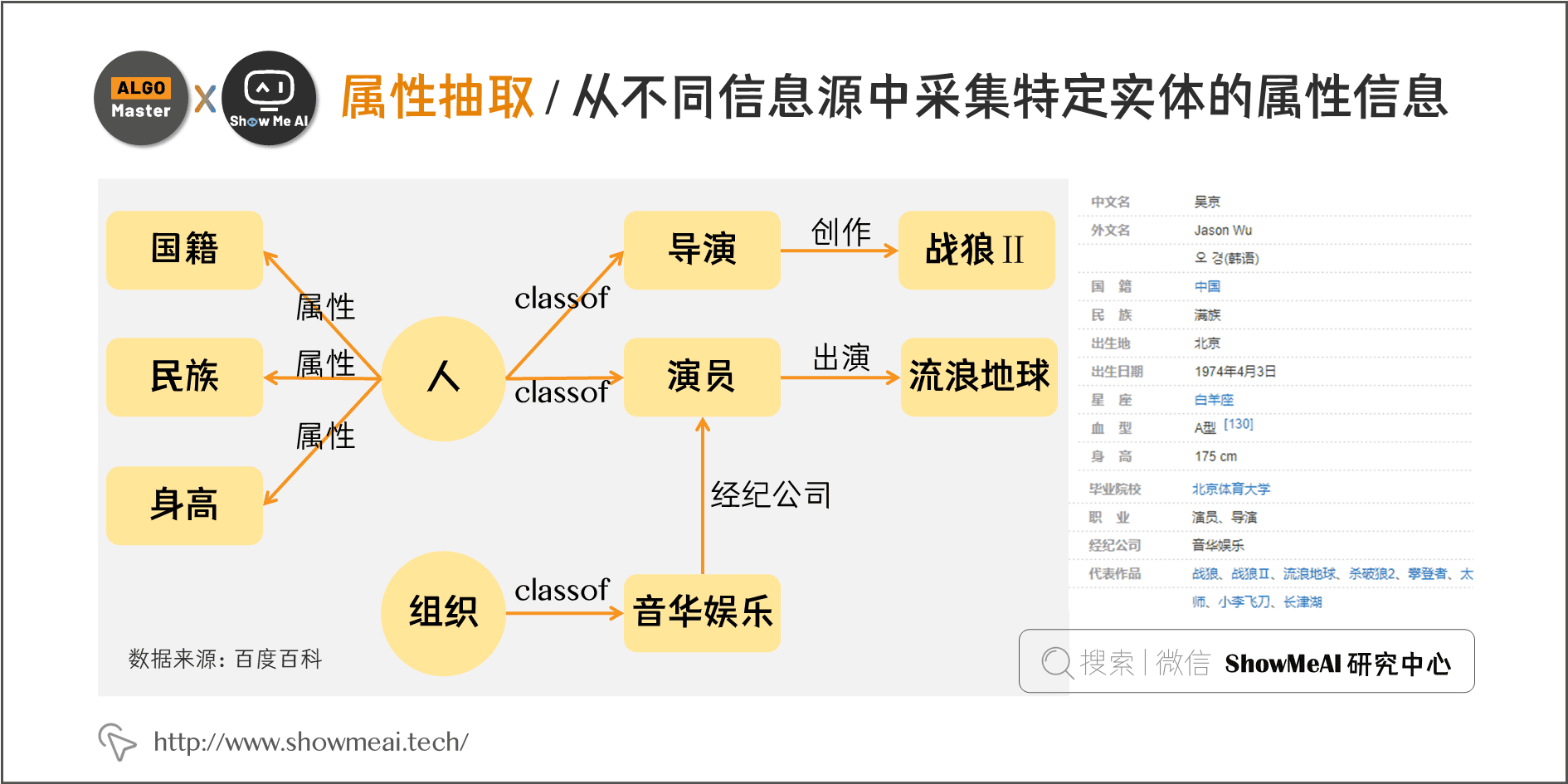
知识图谱学习总结
1 知识图谱的介绍 知识图谱,是结构化的语义知识库,用于迅速描述物理世界中的概念及其相互关系,通过知识图谱能够将Web上的信息、数据以及链接关系聚集为知识,使信息资源更易于计算、理解以及评价,并能实现知识的快速响…...

2021-10-23 51单片机LED1-8按秒递增闪烁
缘由51单片机,八个LED灯按LED1亮1s灭1s,LED1亮2s 灭2s以此类推的方式亮灭-编程语言-CSDN问答 #include "REG52.h" sbit K1 P1^0; sbit K2 P1^1; sbit K3 P1^2; sbit K4 P1^3; sbit P1_0P2^0; sbit P1_1P2^1; sbit P1_2P2^2; sbit P1_3P2^3; sbit P1_…...

在Linux中宏观的看待线程
线程一旦被创建,几乎所有的资源都是被所有的线程共享的。线程也一定要有自己私有的资源,什么样的资源应该是线程私有的? 1.PCB属性私有 2.要有一定的私有上下文结构 3.每个线程都要有独立的栈结构 ps -aL ##1. Linux线程概念 ###什么是线程…...

提示libfakeroot.so或libfakeroot-sysv.so出错处理方法
在RK3588 Buildroot SDK里面,uboot和kernel使用的是prebuild目录下的交叉编译链,而buildroot和APP编译则使用Buildroot生成的交叉编译链来编译(如:位于buildroot/output/rockchip_rk3588/host目录为交叉编译工具链目录)…...

【计算机网络】什么是socket编程?以及相关接口详解
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...

LeetCode.19.删除链表的倒数第n个节点
题目描述: 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点 输入输出实例: 思路:这道题目我们可以用双指针来做,让first和second指针之间的距离为n1,然后我们first和second指针…...

vue-cesium
vue-cesium: Vue 3.x components for CesiumJS. cesium 文档中文版 ArcGisMapServerImageryProvider - Cesium Documentation all参考 https://juejin.cn/post/7258119652726341669 cesium官网 Cesium Sandcastle...

《npm 学习过程中遇到的诸多问题》
npm 开发 1.开发过程中难免会使用到npm ,进行安装第三方包 遇到的问题 match 报错:npm i报错npm ERR! Cannot read property match of undefined 可以尝试清除本地的package-log.json 文件,再试试...

CentOS 介绍
引出 Linux 系统内核与 Linux 发行套件系统的区别? Linux 系统内核指的是一个由 Linus Torvalds(Linux之父,内核主要开发者)负责维护,提供硬件抽象层、磁盘、文件系统控制及多任务功能的系统核心程序。 Linux 发行套…...

模拟面试题1
目录 一、JVM的内存结构? 二、类加载器分为哪几类? 三、讲一下双亲委派机制 为什么要有双亲委派机制? 那你知道有违反双亲委派的例子吗? 四、IO 有哪些类型? 五、Spring Boot启动机制 六、Spring Boot的可执行…...

CTFHUB-web-RCE-综合过滤练习
开启题目 查看网页源代码发现这次网页对 | 、 && 、 || 、 \ 、 / 、; ,都进行了过滤处理 发现换行符 %0a 和回车符 %0d 可以进行测试,在 URL 后面拼接访问 127.0.0.1%0als 用 ls flag_is_here 查看 flag 文件中的内容,发现回显为空…...

Leetcode75-7 除自身以外数组的乘积
没做出来 本来的思路是遍历一遍得到所有乘积和然后除就行 但是题目不能用除法 答案的思路 for(int i0;i<n;i) //最终每个元素其左右乘积进行相乘得出结果{res[i]*left; //乘以其左边的乘积left*nums[i];res[n-1-i]*right; //乘以其右边的乘积right*nums[n-1-i]…...

AI绘画工具介绍:以新奇角度分析与探索AI绘画艺术与技术的交汇点
目录 前言 一、AI绘画工具的前沿技术 1.1 深度学习的进化 1.2 GANs的创新应用 1.3 风格迁移的多样化 1.4 交互式AI绘画的智能化 二、艺术与技术的交汇点 2.1 艺术创作的普及化 2.2 艺术风格的创新 2.3 艺术与科技的深度融合 三、新颖的思考角度 3.1 AI作为艺术创作…...

基于Springboot + Vue的宿舍管理系统
前言 文末获取源码数据库 感兴趣的可以先收藏起来,需要学编程的可以给我留言咨询,希望帮助更多的人 精彩专栏推荐订阅 不然下次找不到哟 Java精品毕设原创实战项目 作者的B站地址:程序员云翼的个人空间-程序员云翼个人主页-哔哩哔哩视频 csd…...

CTFHUB-web-RCE-eval执行
开启题目 查看源码发现直接用蚁剑连接就可以,连接之后发现成功了...

Oracle DBA常用 sql
文章目录 一、基础环境二、常用 sql三、参考资料 版权声明:本文为CSDN博主「杨群」的原创文章,遵循 CC 4.0 BY-SA版权协议,于2023年7月6日首发于CSDN,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.n…...

MindSearch:AI 时代的“思考型”搜索引擎
随着AI技术的飞速发展,搜索引擎领域也迎来了新的变革。继 OpenAI 发布 SearchGPT 之后,国内也涌现出一批优秀的AI搜索引擎,其中,由中科大和上海人工智能实验室联合研发的 MindSearch(思索)尤为引人注目。这…...
:基于SVM 的肥胖风险分类)
机器学习练手(四):基于SVM 的肥胖风险分类
总结:本文为和鲸python 机器学习原理与实践闯关训练营资料整理而来,加入了自己的理解(by GPT4o) 原活动链接 原作者:vgbhfive,多年风控引擎研发及金融模型开发经验,现任某公司风控研发工程师&…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
