当前位置： 首页 > news >正文

让B站直接变成一个纯粹的音乐平台的简单小方法

news 2026/2/9 4:56:52

可能在大多数人眼里，B站就是一个内容丰富的高质量视频平台

但实际上B站还是一个“音乐平台”，只不过大多数时候都是以视频的形式呈现，所以你们可能对此没啥感觉。

那么今天给大家分享一款神级插件，让B站变成一个纯粹的音乐平台，给你带来前所未有的体验~

ENO-M（浏览器插件）

这是一款来自谷歌商店的最新插件，目前用户并不多，只有4个评分，但打的都是满分，说明还是挺受用户认可的(不排除水军的可能)

安装完成以后，只需点击插件图标即可打开新世界大门~

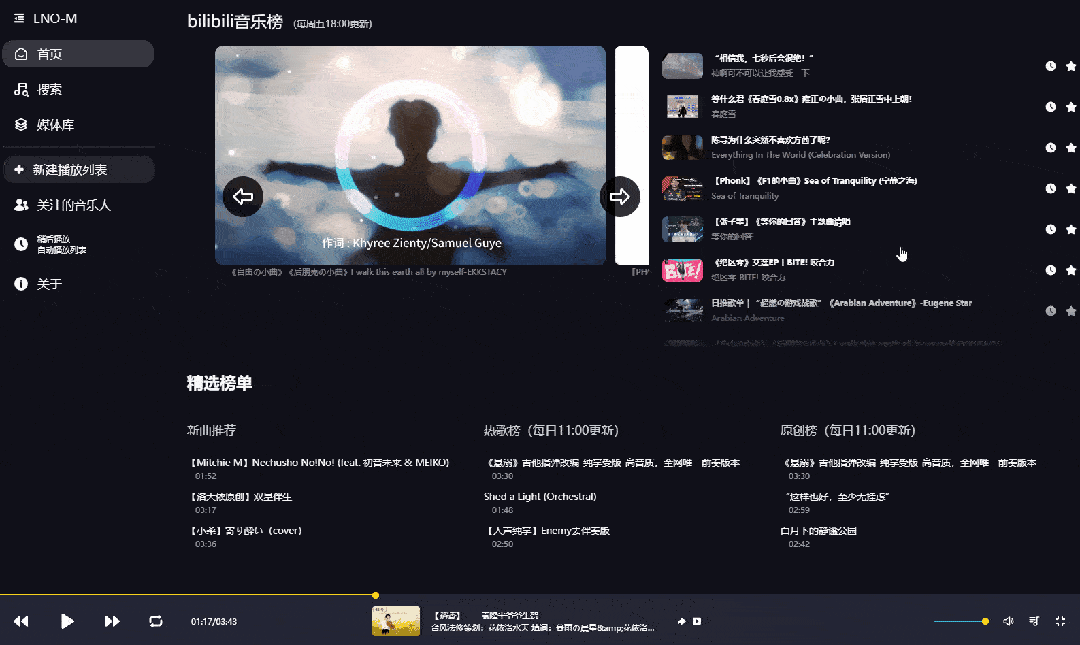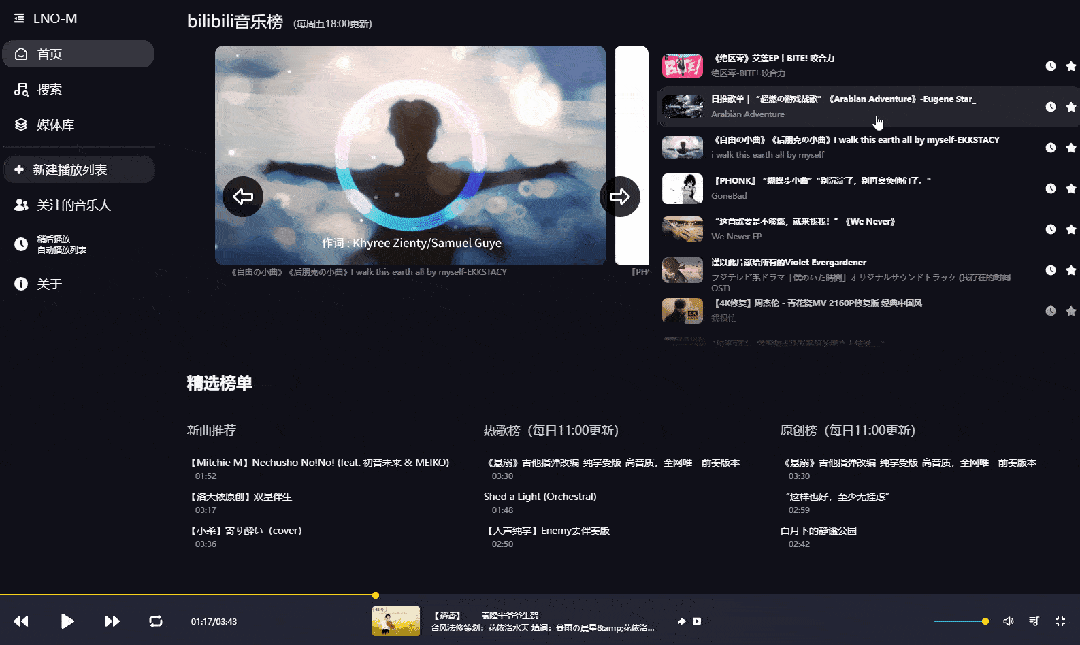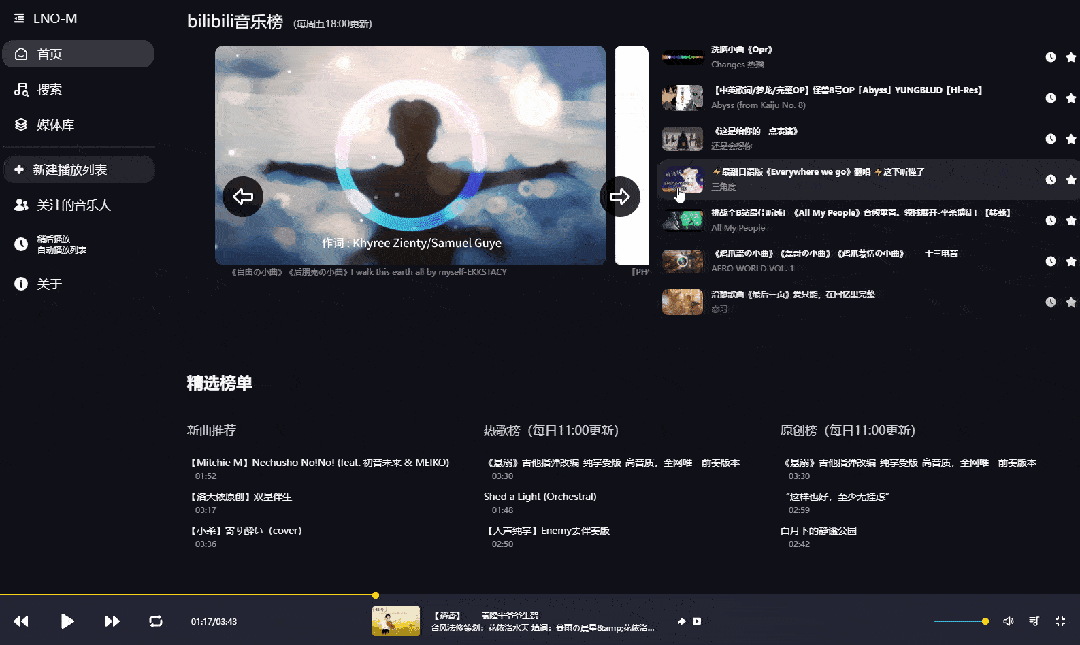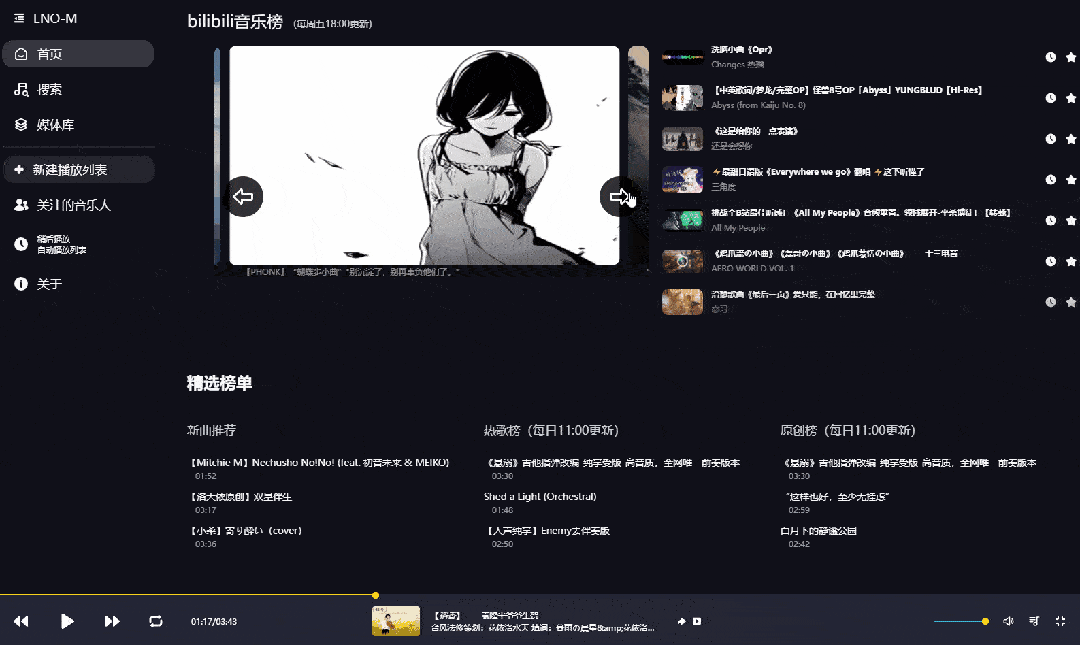
是的，你没看错，下面这个页面是改造后的B站界面，没有了视频推荐，取而代之的是各种音乐排行榜单，是不是有内味儿了？

由于里面的歌曲内容都来源于B站，所以点击底部的按钮还可以查看原视频。

其实说白了播放的并不是歌曲文件，而是以音乐播放器的形式来播放视频，但咱们不会有任何违和感

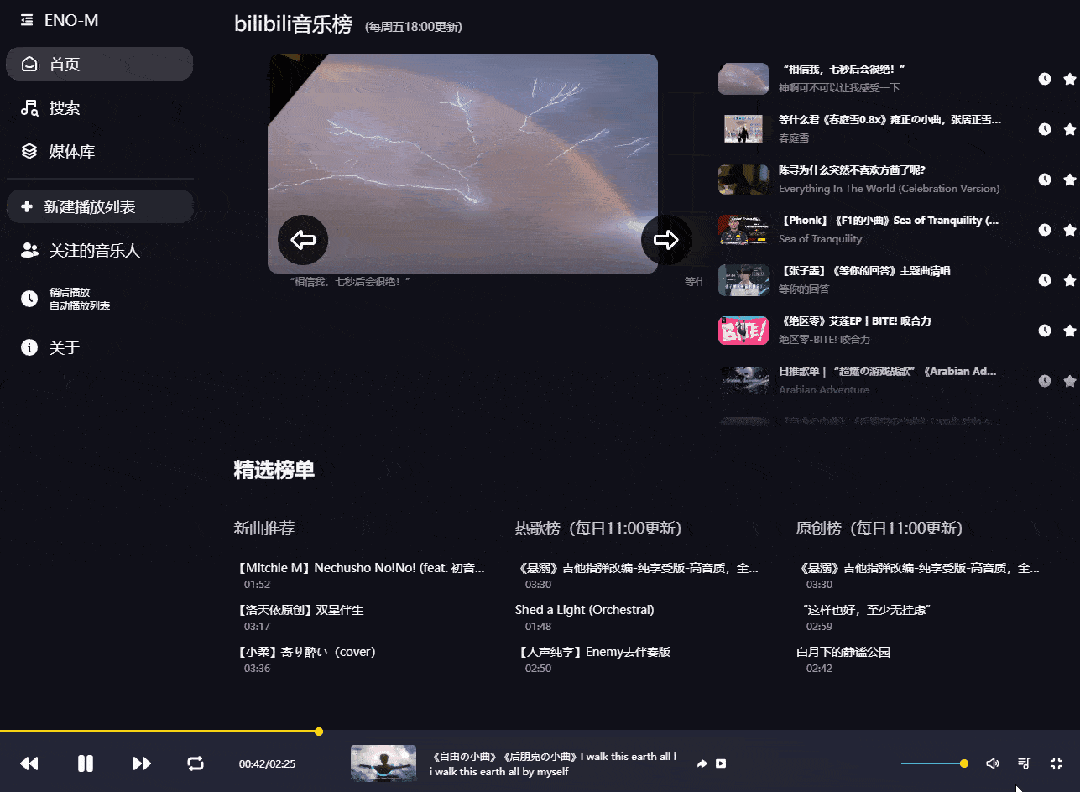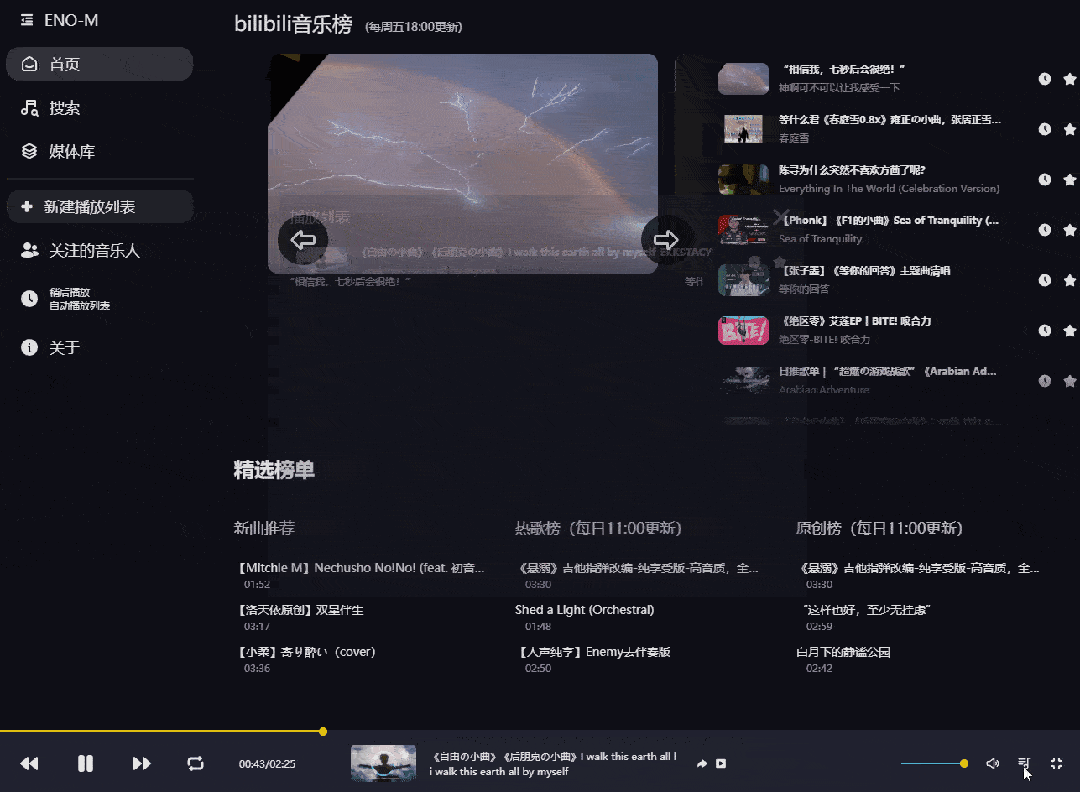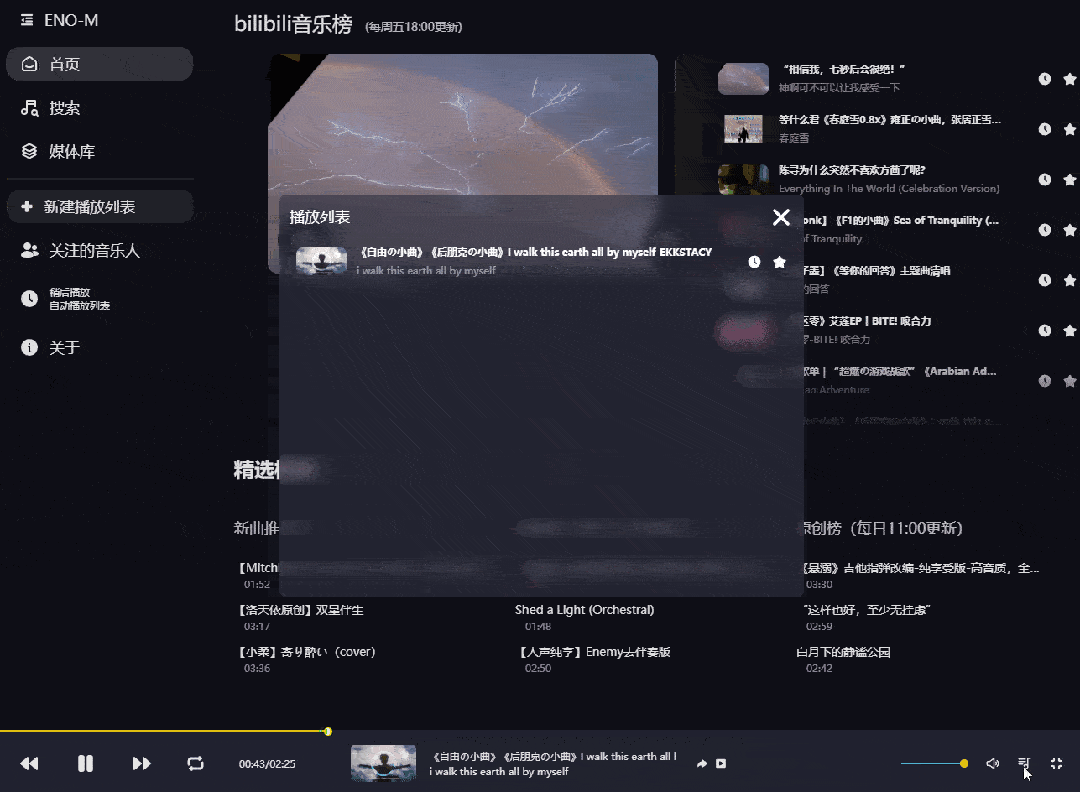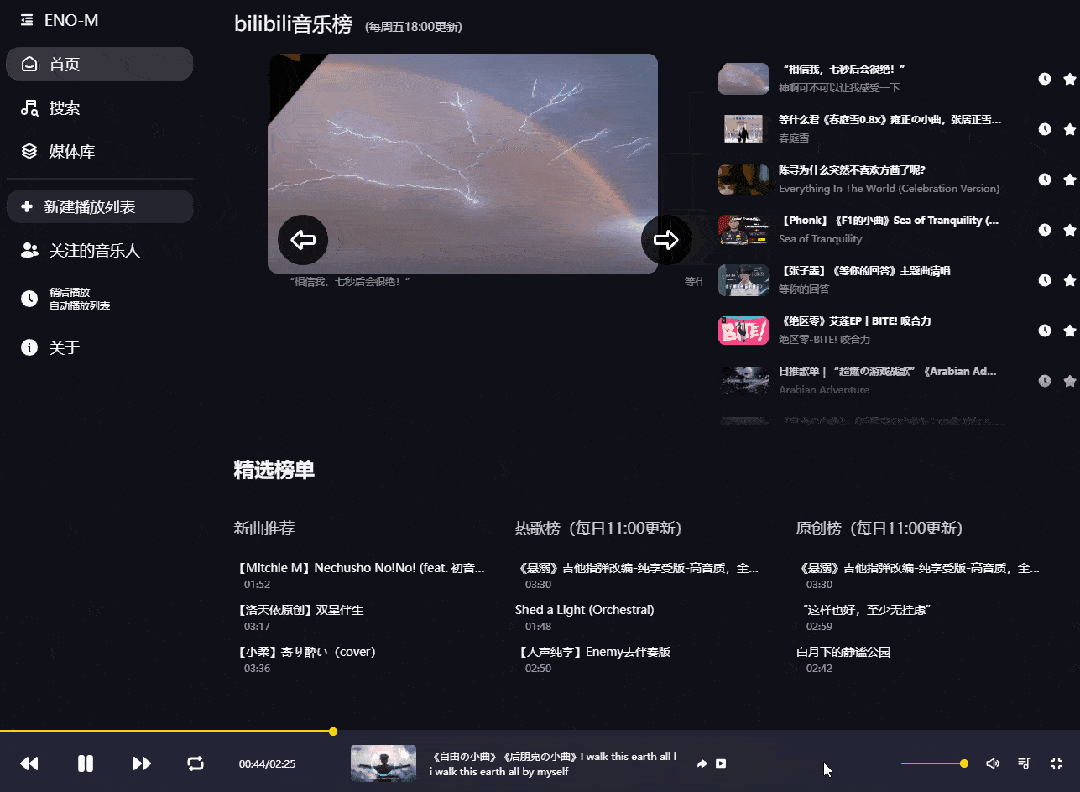
既然是音乐播放器，那么必然少不了「搜索功能」，你甚至还可以在这里白嫖周董的无损音乐，并且连MV都是60帧修复版。

当然，说到底还得归功于B站里热心的大佬

使用这款插件其实在一定程度上比用那些第三方的音乐APP要更为靠谱，不仅音乐资源很丰富，而且还不用担心版权风险。

毕竟里面的资源全都来源于B站，只不过换了种形式展现出来罢了~

相关文章：

让B站直接变成一个纯粹的音乐平台的简单小方法

可能在大多数人眼里，B站就是一个内容丰富的高质量视频平台 但实际上B站还是一个“音乐平台”，只不过大多数时候都是以视频的形式呈现，所以你们可能对此没啥感觉。 那么今天给大家分享一款神级插件，让B站变成一个纯粹的音乐平台&a…...

编程日记 2024/8/8 11:08:10

【MySQL 01】在 Ubuntu 22.04 环境下安装 MySQL

文章目录 🌈 1. 说明🌈 2. 卸载不必要的环境🌈 3. 安装 MySQL🌈 4. 启动和关闭 MySQL 服务🌈 5. 临时登录 MySQL🌈 6. 设置 MySQL 密码🌈 7. 配置 MySQL 🌈 1. 说明 在安装与卸载中…...

编程日记 2024/8/8 11:05:04

linux命令 根据某一字段去掉txt中重复的数据

前提： 文档为格式化好的数据。比如一行是一个json。 判断总共有多少行数据： grep No f.txt | wc -l 查询重复数据有多少行： grep No f.txt | sort -u | wc -l 找到重复的那行数据：(如果每行的json数据大，可忽略此操…...

编程日记 2024/8/8 11:03:01

LVS（Linux virual server）

一：环境准备： rhel9 软件：httpd， ipvsadm 四台纯净的rhel9机子：一台LVS调度设备（双网卡），两台webserver（单网卡仅主机），一台客户机 DR模式多…...

编程日记 2024/8/8 11:00:56

End-to-End Object Detection with Transformers(Detection Transformer)翻译

摘要 我们提出了一种新方法，将目标检测视为直接的集合预测问题。我们的方法简化了检测流程，有效消除了对许多手工设计组件的需求，如非极大值抑制过程或锚框生成，这些组件显式编码了我们对任务的先验知识。新框架称为检测变换器&a…...

编程日记 2024/8/8 10:59:54

uniapp打开地图直接获取位置

uniapp官网文档 https://en.uniapp.dcloud.io/api/location/open-location.html <view class"map-content" click.stop"kilometer(item)"><view class"km">{{item.distance||0}}km</view></view>import map from ../../…...

编程日记 2024/8/8 10:56:51

Qt的事件处理机制、信号和槽以及两者之间的区别

Qt的事件处理机制 Qt 的事件处理机制是其框架的核心部分之一&#xff0c;用于处理用户操作、系统事件以及其他各种事件。以下是 Qt 事件处理机制的关键组成部分和流程&#xff1a; 事件对象 (QEvent)&#xff1a; 所有事件在 Qt 中都是通过事件对象来表示的。QEvent 是所有事…...

编程日记 2024/8/8 10:55:50

LSTM实战之预测股票

&#x1f4c8; 用PyTorch搭建LSTM模型&#xff0c;轻松预测股票价格&#xff01;&#x1f680; Hey小伙伴们&#xff0c;今天给大家带来一个超级实用的项目教程——如何用PyTorch和LSTM模型来预测股票价格&#xff01;&#x1f31f; &#x1f50d; 项目背景 我们都知道股市是…...

编程日记 2024/8/8 10:54:49

30-50K｜抖音大模型｜社招3轮面经

情况介绍&#xff1a;我主要做nlp&#xff0c;也涉及到多模态和强化学习。现在大环境比较差&#xff0c;能投的公司不是很多&#xff0c;比如腾讯&#xff0c;主要还是高级别的&#xff0c;所以腾讯我就没投 抖音一面 1、聊项目。 2、AUC的两种公式是&#xff1f;你能证明这…...

编程日记 2024/8/8 10:51:45

ChatGPT首次被植入人类大脑：帮助残障人士开启对话

马斯克在脑机接口中最强大的竞争对手Synchron有了新的技术进展&#xff0c;他们首次将ChatGPT整合到其脑机系统中&#xff0c;以使瘫痪患者更容易控制他们的数字设备。Synchron凭借其独特的脑机接口&#xff08;BCI&#xff09;技术脱颖而出&#xff0c;该技术巧妙地运用了成熟…...

编程日记 2024/8/8 10:50:44

数据结构-常见排序的七大排序

1.排序的概念及其运用 1.1排序的概念 排序&#xff1a;所谓排序&#xff0c;就是使一串记录&#xff0c;按照其中的某个或某些关键字的大小&#xff0c;递增或递减的排列起来的操作。 稳定性&#xff1a;假定在待排序的记录序列中&#xff0c;存在多个具有相同的关键字的记录…...

编程日记 2024/8/8 10:47:40

程序员学CFA——财务报告与分析（四）

财务报告与分析&#xff08;四&#xff09; 资产负债表资产负债表的构成和格式资产负债表的要素资产负债所有者权益 资产负债表的格式分层的资产负债表基于流动性的资产负债表 资产的计量属性资产负债表科目金融资产持有至到期投资交易性金融资产可供出售金融资产 商誉少数股东…...

编程日记 2024/8/8 10:46:38

【消息队列】kafka如何保证消息不丢失？

&#x1f44f;大家好&#xff01;我是和风coding&#xff0c;希望我的文章能给你带来帮助&#xff01; &#x1f525;如果感觉博主的文章还不错的话&#xff0c;请&#x1f44d;三连支持&#x1f44d;一下博主哦 &#x1f4dd;点击 我的主页 还可以看到和风的其他内容噢&#x…...

编程日记 2024/8/8 10:45:37

不同随机数生成的含义

torch.manual_seed(all_args.seed) torch.cuda.manual_seed(all_args.seed) torch.cuda.manual_seed_all(all_args.seed) np.random.seed(all_args.seed) random.seed(all_args.seed) 这几种随机种子设置的含义如下&#xff1a; torch.manual_seed(all_args.seed): 设置PyTor…...

编程日记 2024/8/8 10:44:35

Jar工具完全指南：从入门到精通

Jar工具完全指南&#xff1a;从入门到精通的详尽教程 前言 欢迎来到Jar工具的完全指南&#xff01;无论你是Java编程的初学者&#xff0c;还是经验丰富的开发者&#xff0c;掌握Jar工具都是必不可少的。Jar&#xff08;Java Archive&#xff09;是Java生态系统中的一个核心组…...

编程日记 2024/8/8 10:43:34

前端使用docx-preview展示docx + 后端doc转docx

文章目录 后端 doc 转 docxdcox - preview安装导入使用注意 最近菜鸟刚搞完签字&#xff0c;结果需求就加了&#xff0c;如果合同有附件&#xff08;.doc.docx&#xff09;&#xff0c;签名就是签到附件里面&#xff0c;没有附件才是签到那个html里面&#xff01; 这里附件签名…...

编程日记 2024/8/8 10:41:32

Vue3 组件通信

目录 create-vue创建项目 一. 父子通信 1. 父传子 2. 子传父 二. 模版引用(通过ref获取实例对象) 1.基本使用 2.defineExpose 三. 跨层通信 - provide和inject 1. 作用和场景 2. 跨层传递普通数据 3. 跨层传递响应式数据 4. 跨层传递方法 create-vue创建项目 npm ini…...

编程日记 2024/8/8 10:38:28

如何在Ubuntu 14.04上安装、配置和部署Rocket.Chat

前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家。点击跳转到网站。 简介 Rocket.Chat 是一个使用 Meteor 构建的开源消息应用程序。它支持视频会议、文件共享、语音消息&#xff0c;具有完整的 API 等功能…...

编程日记 2024/8/8 10:35:24

ISO 26262中的失效率计算：IEC TR 62380-Section 15-Switches and keyboards

目录 概要 1 开关和键盘的分类 2 开关和键盘失效率的计算 2.1 Switches and keyboards 2.1.1 Base失效率 2.1.2 接触数量 2.1.3 温度循环De-rating系数 概要 IEC TR 62380《电子组件、PCBs和设备的可靠性预计通用模型》是涵盖电路、半导体分立器件、光电组件、电阻器、电…...

编程日记 2024/8/8 10:33:22

Linux安全与高级应用（五）深入探讨Linux Shell脚本应用：从基础到高级

文章目录 深入探讨Linux Shell脚本应用&#xff1a;从基础到高级引言一、Shell脚本基础知识1. Shell的作用与分类2. 编写第一个Shell脚本 二、Shell变量的使用1. 变量的类型与定义2. 引号的使用3. 位置变量与预定义变量 三、重定向与管道操作1. 重定向操作2. 管道操作 四、计划…...

编程日记 2024/8/8 10:30:18

MFC内存泄露

1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

编程新知 2026/1/22 15:14:25

【HarmonyOS 5.0】DevEco Testing：鸿蒙应用质量保障的终极武器

——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的​​一体化测试平台​​&#xff0c;覆盖应用全生命周期测试需求&#xff0c;主要提供五大核心能力&#xff1a; ​​测试类型​​​​检测目标​​​​关键指标​​功能体验基…...

编程新知 2026/1/28 8:17:53

CMake基础：构建流程详解

目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

编程新知 2026/2/2 7:39:34

dedecms 织梦自定义表单留言增加ajax验证码功能

增加ajax功能模块&#xff0c;用户不点击提交按钮&#xff0c;只要输入框失去焦点&#xff0c;就会提前提示验证码是否正确。 一&#xff0c;模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

编程新知 2026/2/5 17:51:52

微服务商城-商品微服务

数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

编程新知 2026/1/29 18:30:30

华为云Flexus+DeepSeek征文｜DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建

华为云FlexusDeepSeek征文&#xff5c;DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色&#xff0c;华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型&#xff0c;能助力我们轻松驾驭 DeepSeek-V3/R1&#xff0c;本文中将分享如何…...

编程新知 2026/2/2 2:30:58

什么是Ansible Jinja2

理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具&#xff0c;可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板&#xff0c;允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板&#xff0c;并通…...

编程新知 2026/2/6 1:00:25

使用 SymPy 进行向量和矩阵的高级操作

在科学计算和工程领域&#xff0c;向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能&#xff0c;能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作&#xff0c;并通过具体…...

编程新知 2026/2/8 21:52:30

Android第十三次面试总结（四大 组件基础）

Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成&#xff0c;用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机&#xff1a; ​onCreate()​​ ​调用时机​&#xff1a;Activity 首次创建时调用。​…...

编程新知 2025/10/15 15:07:34

对象回调初步研究

_OBJECT_TYPE结构分析 在介绍什么是对象回调前&#xff0c;首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例&#xff0c;用_OBJECT_TYPE这个结构来解析它&#xff0c;0x80处就是今天要介绍的回调链表&#xff0c;但是先不着急&#xff0c;先把目光…...

编程新知 2026/1/26 18:44:47