24/8/7 算法笔记 支持向量机回归问题天猫双十一
import numpy as np
from sklearn.svm import SVR
import matplotlib.pyplot as pltX = np.linspace(0,2*np.pi,50).reshape(-1,1)
y = np.sin(X)
plt.scatter(X,y)
建模
线性核函数
svr = SVR(kernel = 'linear')
svr.fit(X,y.ravel())#变成一维y_ = svr.predict(X)
plt.scatter(X,y)plt.plot(X,y_,color='red')
poly多项式核函数
svr = SVR(kernel = 'poly',degree=2)
svr.fit(X,y.ravel())#变成一维y_ = svr.predict(X)
plt.scatter(X,y)plt.plot(X,y_,color='red')
rbf高斯核函数
svr = SVR(kernel = 'rbf')
svr.fit(X,y.ravel())y_ = svr.predict(X)
plt.scatter(X,y)plt.plot(X,y_,color='red')
天猫双十一销量数据
X= np.arange(2009,2020) - 2008
y = np.array([0.5,9.36,52,191,350,571,912,1207,1632,2135,2684])
plt.scatter(X,y,color = 'red')
标准化
X_test=np.linspace(2009,2019,100).reshape(-1,1)-2008svr = SVR(kernel = 'linear')
svr.fit(X.reshape(-1,1),y)y_= svr.predict(X_test)plt.scatter(X,y,color = 'red')plt.plot(X_test.ravel(),y_,color='green')
svr = SVR(kernel = 'rbf')
svr.fit(X.reshape(-1,1),y)y_= svr.predict(X_test)plt.scatter(X,y,color = 'red')plt.plot(X_test.ravel(),y_,color='green')
svr = SVR(kernel = 'poly',coef0=200)#多项式
svr.fit(X.reshape(-1,1),y)y_= svr.predict(X_test)plt.scatter(X,y,color = 'red')plt.plot(X_test.ravel(),y_,color='green')
可以看见poly核函数最好
在机器学习中,特别是在支持向量机(SVM)算法中,核函数是一种将数据从原始特征空间映射到更高维特征空间的数学函数,以便在新的空间中更容易地进行线性分割。以下是三种常见核函数的区别:
-
线性核函数(Linear Kernel):
- 公式:K(x,y)=x⋅yK(x,y)=x⋅y
- 描述:线性核函数实际上不进行映射,它直接在原始特征空间中计算两个点的点积。这意味着它不会增加特征的维度。
- 适用情况:当数据已经是线性可分的,或者特征空间的维度不是问题时,线性核函数是一个很好的选择。
-
多项式核函数(Polynomial Kernel,也称为Poly Kernel):
- 公式:K(x,y)=(γ⋅x⋅y+r)dK(x,y)=(γ⋅x⋅y+r)d
- 参数:γγ 是核函数的系数,rr 是偏置项,dd 是多项式的度数。
- 描述:多项式核函数将数据映射到一个多项式特征空间。通过调整度数 dd,可以控制映射后的维度和复杂性。
- 适用情况:当数据具有非线性特征,需要通过增加特征的组合来提高模型的表达能力时。
-
径向基函数(Radial Basis Function,RBF或Gaussian Kernel):
- 公式:K(x,y)=exp(−γ∥x−y∥2)K(x,y)=exp(−γ∥x−y∥2)
- 参数:γγ 是核函数的系数,控制了高斯函数的宽度。
- 描述:RBF核函数通过计算两个点之间的欧几里得距离的平方,并将其作为指数函数的输入,从而实现非线性映射。这种核函数可以捕捉数据中的复杂模式。
- 适用情况:RBF核是SVM中最常用的核函数之一,适用于大多数非线性问题,特别是当数据的分布不是线性的,或者需要捕捉更复杂的边界时。
每种核函数都有其特点和适用场景。选择哪种核函数通常取决于数据的特性和问题的需求。在实践中,可能需要通过交叉验证等方法来确定最佳的核函数和参数。
相关文章:

24/8/7 算法笔记 支持向量机回归问题天猫双十一
import numpy as np from sklearn.svm import SVR import matplotlib.pyplot as plt X np.linspace(0,2*np.pi,50).reshape(-1,1) y np.sin(X) plt.scatter(X,y) 建模 线性核函数 svr SVR(kernel linear) svr.fit(X,y.ravel())#变成一维y_ svr.predict(X) plt.scatter(…...

win7系统利用定时启动+脚本实现MySQL文件自动备份
前言 最近接到项目,数据量不大但对运行数据的安全性要求极高,为避免因不可抗拒因素导致的数据丢失,选择机械硬盘作为数据存储盘,并使用脚本方式对文件进行备份 一、脚本 下面为自动备份文件的 脚本,可根据自身情况进…...

基于Java多线程处理数据
基于Java多线程处理数据 背景代码实现 背景 在日常工作中,有一个同步企微客户-学员关系接口的定时任务在执行中随着数据量的不断增长,定时任务的执行结束时间也出现了当天执行不完的情况,影响到了正常业务的运行。基于这种情况,在…...

日常知识点之遇到问题结构体按位构造协议时和期望不一致,研究记录一下
遇到一个问题,在做业务的时候,涉及到协议相关,按位进行设计,用结构体来模拟协议时,发现内存存储和实际目的不一致,知道是大小端以及计算机底层存储逻辑相关,所以研究了一下。 1:简单…...

spring mvc 文件下载
在web中下载的方式大多基于servlet,在web.xml中配置下载路径,这里再介绍json(转成base64字符串)和blob的使用方式 servlet WEB-INF/web.xml <!--url映射--> <servlet-mapping><servlet-name>DowloadServlet</servlet-name>&l…...

Qt WebEngine基于WebEngineScript注入js脚本
在之前的文章中,我们介绍了Qt WebEngine注入js的用法,及runJavaScript()的用法,该方法主要是用在页面加载完成后,为了和网页做一些交互时使用。有时候需要监听网页加载完成的一些状态或信息,则需要网页加载前注入js来实…...
案例分享-国外UI设计界面赏析
国外UI设计倾向于简洁的布局和清晰的排版,减少视觉干扰,提升用户体验。通过合理的色彩搭配和图标设计,营造舒适愉悦的使用氛围。 设计师不拘泥于传统框架,勇于尝试新元素和理念,使界面独特有趣。同时,强调以…...
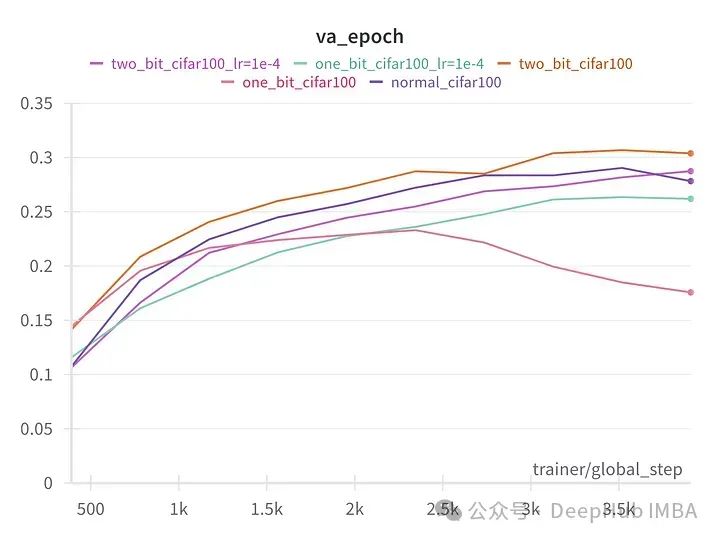
用PyTorch 从零开始构建 BitNet 1.58bit
我们手动实现BitNet的编写,并进行的一系列小实验证实,看看1.58bit 模型是否与全精度的大型语言模型相媲美! 什么是量化以及为什么需要它? 量化是用更少的比特数表示浮点数的过程。当两个数字使用不同的比特数进行量化时…...

信创安全 | 新一代内网安全方案—零信任沙盒
在当今数字化时代,访问安全和数据安全成为企业面临的重要挑战。传统的边界防御已经无法满足日益复杂的内网办公环境,层出不穷的攻击手段已经让市场单一的防御手段黔驴技穷。当企业面临越来越复杂的网络威胁和数据泄密风险时,更需要一种综合的…...
)
Redis的回收策略(淘汰策略)
volatile-lru :从已设置过期时间的数据集( server.db[i].expires )中挑选最近最少使用的数据淘汰 volatile-ttl : 从已设置过期时间的数据集( server.db[i].expires ) 中挑选将要过期的数据淘汰 volatile…...

Electron-builder 打包
项目比较简单,仅使用了 Electron 原生js 安装 electron-builder npm install electron-builder --dev配置 package.json 中的打包命令 {"script":{// ..."dev": "electron .","pack": "electron-builder"} }添…...

笔试练习day3
目录 BC149 简写单词题目解析代码 dd爱框框题目解析解析代码方法一暴力解法方法二同向双指针(滑动窗口) 除2!题目解析解法模拟贪心堆 感谢各位大佬对我的支持,如果我的文章对你有用,欢迎点击以下链接 🐒🐒🐒 个人主页 🥸…...

企业想要将大模型技术应用到企业管理中需具备什么条件?
#企业 #企业管理 #大模型 企业想要将大模型技术应用到企业管理中,需要考虑以下几个关键条件: 1.明确的需求定位:企业应首先诊断自身的业务场景、数据、算法、基础设施预算以及战略等能力,明确大模型能够为企业带来的具体赋…...

go 事件机制(观察者设计模式)
背景: 公司目前有个业务,收到数据后,要分发给所有的客户端或者是业务模块,类似消息通知这样的需求,自然而然就想到了事件,观察者比较简单就自己实现以下,确保最小功能使用支持即可,其…...

RISC-V竞赛|第二届 RISC-V 软件移植及优化锦标赛报名正式开始!
目录 赛事背景 赛道方向 适配夺旗赛 优化竞速赛 比赛赛题(总奖金池8万元!) 🔥竞速赛 - OceanBase 移植与优化 比赛赛程(暂定) 赛事说明 「赛事背景」 为了推动 RISC-V 软件生态更快地发展࿰…...

【VTK】ubuntu手动编译VTK9.3 Generating qmltypes file 失败
环境 硬件:Jetson Xavier NX 套件 系统:Ubuntu 20.04 软件 :QT5.15.6 解决 0、问题 最近在Jetson Xavier NX 套件上编译VTK库,因为想要配合QQuick使用,所以cmake配置时勾选了VTK_MODULE_ENABLE_VTK_GUISupportQtQu…...

学习java的日子 Day64 学生管理系统 web2.0 web版本
MVC设计模式 概念 - 代码的分层 MVC:项目分层的思想 字母表示层理解MModle模型层业务的具体实现VView视图层展示数据CController控制器层控制业务流程(跳转) 1.细化理解层数 Controller:控制器层,用于存放Servlet&…...

【第14章】Spring Cloud之Gateway路由断言(IP黑名单)
文章目录 前言一、内置路由断言1. 案例(Weight)2. 更多断言 二、自定义路由断言1. 黑名单断言2. 全局异常处理3. 应用配置4. 单元测试 总结 前言 Spring Cloud Gateway可以让我们根据请求内容精确匹配到对应路由服务,官方已经内置了很多路由断言,我们也…...

3、pnpm yarn npm
项目里实际上就只有这些依赖 node module 里却有很多的包 原因: 比如说vue,vue内部有依赖了其余的包。工具又依赖了别的依赖 造成的问题:我可以直接去用这个包,但是这个包在package.json中却没有看到-----幽灵依赖 那如果说别…...

❄️5. Kubernetes核心资源之名称空间和Pod实战
**什么是名称空间Namespace: ** Namespace是k8s系统中的一种非常重要资源,它的主要作用是用来实现多套环境的资源隔离或者多用户的资源隔离。默认情况下,k8s集群中的所有的Pod都是可以相互访问的。但是在实际中,可能不想让两个Pod之间进行互…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
