使用太极taichi写一个只有一个三角形的有限元
公式来源
https://blog.csdn.net/weixin_43940314/article/details/128935230
GAME103
https://games-cn.org/games103-slides/
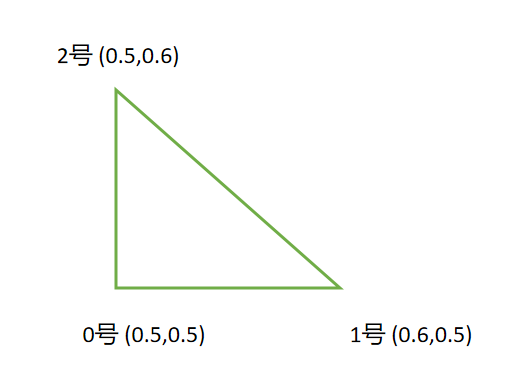
初始化我们的三角形
全局的坐标范围为0-1
我们的三角形如图所示
@ti.kernel
def init():X[0] = [0.5, 0.5]X[1] = [0.5, 0.6]X[2] = [0.6, 0.5]x[0] = X[0] + [0, 0.01]x[1] = X[1]x[2] = X[2]
X是rest pos
x是current pos
这里给一个小的增量是为了看出来被拉了,否则产生不了弹性力
公式抄录
[f1f2]=−ArefFS[X10X20]−T\begin{bmatrix} \mathbf{f_1} & \mathbf{f_2} \end{bmatrix}= -A^{ref} \mathbf{F} \mathbf{S } \begin{bmatrix} \mathbf{X_{10}} & \mathbf{X_{20}} \end{bmatrix}^{-T} [f1f2]=−ArefFS[X10X20]−T
F=[x10x20][X10X20]−1F=\begin{bmatrix} x_{10} & x_{20} \end{bmatrix}\begin{bmatrix} X_{10} & X_{20} \end{bmatrix}^{-1} F=[x10x20][X10X20]−1
S=2μG+λtrace(C)IS = 2 \mu G + \lambda trace(C) I S=2μG+λtrace(C)I
G=12(FTF−I)G = \frac{1}{2} (F^T F -I) G=21(FTF−I)
0. 设定一下材料参数
dim=2
n_particles = 3
n_elements = 1
area = 0.1*0.1*0.5
dt = 1e-4
E, nu = 1e3, 0.33 # Young's modulus and Poisson's ratio
mu, lam = E / 2 / (1 + nu), E * nu / (1 + nu) / (1 - 2 * nu) # Lame parameters
1 计算F
根据上面的公式,我们要先算F
@ti.kernel
def substep():#compute deformation gradientfor i in range(n_elements):Dm =ti.Matrix([[x[1][0]-x[0][0], x[2][0]-x[0][0]], [x[1][1]-x[0][1], x[2][1]-x[0][1]]])Dm_inv[i] = Dm.inverse()Ds = ti.Matrix([[X[1][0]-X[0][0], X[2][0]-X[0][0]], [X[1][1]-X[0][1], X[2][1]-X[0][1]]])F[i] = Ds @ Dm_inv[i]
2 计算格林应变
#compute green strain
for i in range(n_elements):G[i] = 0.5 * (F[i].transpose() @ F[i] - ti.Matrix([[1, 0], [0, 1]]))
3 计算PK1
#compute second Piola Kirchhoff stress
for i in range(n_elements):S[i] = 2 * mu *G[i] + lam * (G[i][0,0]+G[i][1,1]) * ti.Matrix([[1, 0], [0, 1]])
4 计算粒子上的力
#compute force(先暂且就计算一个三角形的力,后面再考虑多个三角形的情况)
force_matrix = F[0] @ S[0] @ Dm_inv[0].transpose() * area
force[1] = ti.Vector([force_matrix[0, 0], force_matrix[1, 0]])
force[2] = ti.Vector([force_matrix[0, 1], force_matrix[1, 1]])
force[0] = -force[1] - force[2]
5 加个重力
#gravityfor i in range(n_particles):force[i][1] -= 0.16 时间积分 同时处理边界条件
#time integration(with boundary condition)eps = 0.01for i in range(n_particles):vel[i] += dt * force[i]#boundary conditioncond = (x[i] < eps) & (vel[i] < 0) | (x[i] > 1) & (vel[i] > eps)for j in ti.static(range(dim)):if cond[j]:vel[i][j] = 0 x[i] += dt * vel[i]
完整的程序
# ref: https://blog.csdn.net/weixin_43940314/article/details/128935230import taichi as ti
import numpy as npti.init(arch=ti.cpu, debug=True)dim=2
n_particles = 3
n_elements = 1
area = 0.1*0.1*0.5
# lam = 1
# mu = 1
dt = 1e-4
E, nu = 1e3, 0.33 # Young's modulus and Poisson's ratio
mu, lam = E / 2 / (1 + nu), E * nu / (1 + nu) / (1 - 2 * nu) # Lame parametersx = ti.Vector.field(dim, dtype=float, shape=n_particles) #deformed position
force = ti.Vector.field(dim, dtype=float, shape=n_particles)
vel = ti.Vector.field(dim, dtype=float, shape=n_particles)
X = ti.Vector.field(dim, dtype=float, shape=n_particles) #undeformed position
S = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) #Second Piola Kirchhoff stress
F = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) #deformation gradient
G = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) #green strain@ti.kernel
def init():X[0] = [0.5, 0.5]X[1] = [0.5, 0.6]X[2] = [0.6, 0.5]x[0] = X[0] + [0, 0.01]x[1] = X[1]x[2] = X[2]Dm_inv = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements)
@ti.kernel
def substep():#compute deformation gradientfor i in range(n_elements):Dm =ti.Matrix([[x[1][0]-x[0][0], x[2][0]-x[0][0]], [x[1][1]-x[0][1], x[2][1]-x[0][1]]])Dm_inv[i] = Dm.inverse()Ds = ti.Matrix([[X[1][0]-X[0][0], X[2][0]-X[0][0]], [X[1][1]-X[0][1], X[2][1]-X[0][1]]])F[i] = Ds @ Dm_inv[i]# print(F[0])#compute green strainfor i in range(n_elements):G[i] = 0.5 * (F[i].transpose() @ F[i] - ti.Matrix([[1, 0], [0, 1]]))#compute second Piola Kirchhoff stressfor i in range(n_elements):S[i] = 2 * mu *G[i] + lam * (G[i][0,0]+G[i][1,1]) * ti.Matrix([[1, 0], [0, 1]])#compute force(先暂且就计算一个三角形的力,后面再考虑多个三角形的情况)force_matrix = F[0] @ S[0] @ Dm_inv[0].transpose() * areaforce[1] = ti.Vector([force_matrix[0, 0], force_matrix[1, 0]])force[2] = ti.Vector([force_matrix[0, 1], force_matrix[1, 1]])force[0] = -force[1] - force[2]# print(force[0])#gravityfor i in range(n_particles):force[i][1] -= 0.1#time integration(with boundary condition)eps = 0.01for i in range(n_particles):vel[i] += dt * force[i]#boundary conditioncond = (x[i] < eps) & (vel[i] < 0) | (x[i] > 1) & (vel[i] > eps)for j in ti.static(range(dim)):if cond[j]:vel[i][j] = 0 x[i] += dt * vel[i]def main():init()gui = ti.GUI('my', (1024, 1024))while gui.running:for e in gui.get_events():if e.key == gui.ESCAPE:gui.running = Falseelif e.key == 'r':init()for i in range(30):substep()vertices_ = np.array([[0, 1, 2]], dtype=np.int32)particle_pos = x.to_numpy()a = vertices_.reshape(n_elements * 3)b = np.roll(vertices_, shift=1, axis=1).reshape(n_elements * 3)gui.lines(particle_pos[a], particle_pos[b], radius=1, color=0x4FB99F)gui.circles(particle_pos, radius=5, color=0xF2B134)gui.show()if __name__ == '__main__':main()

相关文章:

使用太极taichi写一个只有一个三角形的有限元
公式来源 https://blog.csdn.net/weixin_43940314/article/details/128935230 GAME103 https://games-cn.org/games103-slides/ 初始化我们的三角形 全局的坐标范围为0-1 我们的三角形如图所示 ti.kernel def init():X[0] [0.5, 0.5]X[1] [0.5, 0.6]X[2] [0.6, 0.5]x[0…...
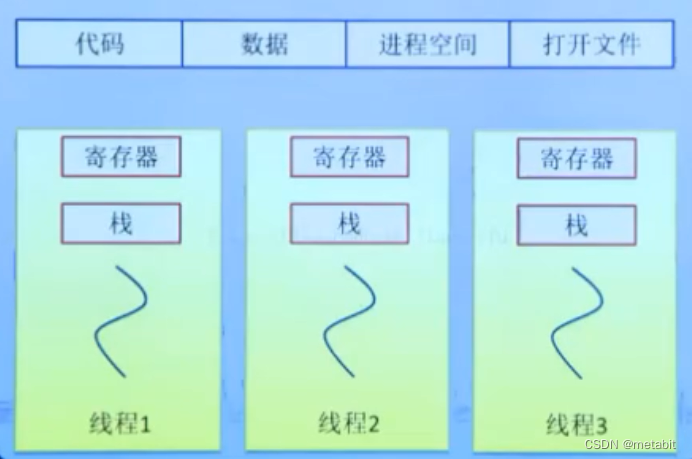
进程,线程
进程是操作系统分配资源的基本单位,线程是CPU调度的基本单位。 PCB:进程控制块,操作系统描述程序的运行状态,通过结构体task,struct{…},统称为PCB(process control block)。是进程管理和控制的…...

第03章_基本的SELECT语句
第03章_基本的SELECT语句 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 1. SQL概述 1.1 SQL背景知识 1946 年,世界上第一台电脑诞生,如今,借由这台电脑发展…...

干货 | 简单了解运算放大器...
运算放大器发明至今已有数十年的历史,从最早的真空管演变为如今的集成电路,它在不同的电子产品中一直发挥着举足轻重的作用。而现如今信息家电、手机、PDA、网络等新兴应用的兴起更是将运算放大器推向了一个新的高度。01 运算放大器简述运算放大器&#…...
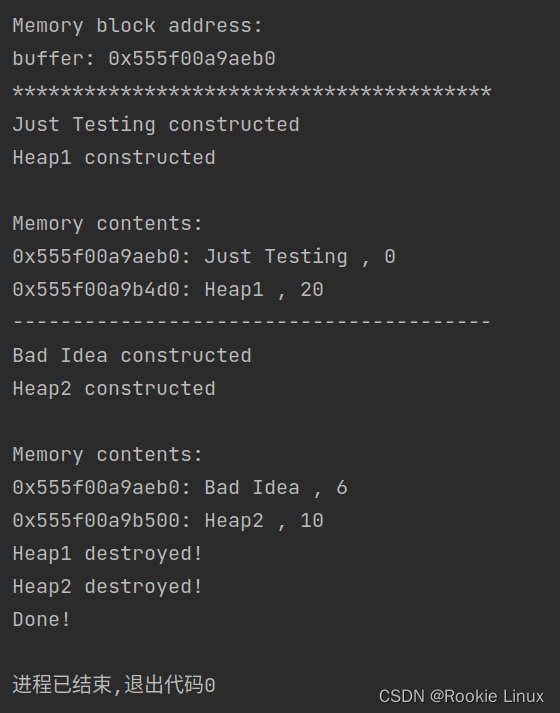
C++定位new用法及注意事项
使用定位new创建对象,显式调用析构函数是必须的,这是析构函数必须被显式调用的少数情形之一!, 另有一点!!!析构函数的调用必须与对象的构造顺序相反!切记!!&a…...

【Android笔记75】Android之翻页标签栏PagerTabStrip组件介绍及其使用
这篇文章,主要介绍Android之翻页标签栏PagerTabStrip组件及其使用。 目录 一、PagerTabStrip翻页标签栏 1.1、PagerTabStrip介绍 1.2、PagerTabStrip的使用 (1)创建布局文件...

【Kafka】【二】消息队列的流派
消息队列的流派 ⽬前消息队列的中间件选型有很多种: rabbitMQ:内部的可玩性(功能性)是⾮常强的rocketMQ: 阿⾥内部⼀个⼤神,根据kafka的内部执⾏原理,⼿写的⼀个消息队列中间 件。性能是与Kaf…...

现代 cmake (cmake 3.x) 操作大全
cmake 是一个跨平台编译工具,它面向各种平台提供适配的编译系统配置文件,进而调用这些编译系统完成编译工作。cmake 进入3.x 版本,指令大量更新,一些老的指令开始被新的指令集替代,并加入了一些更加高效的指令/参数。本…...
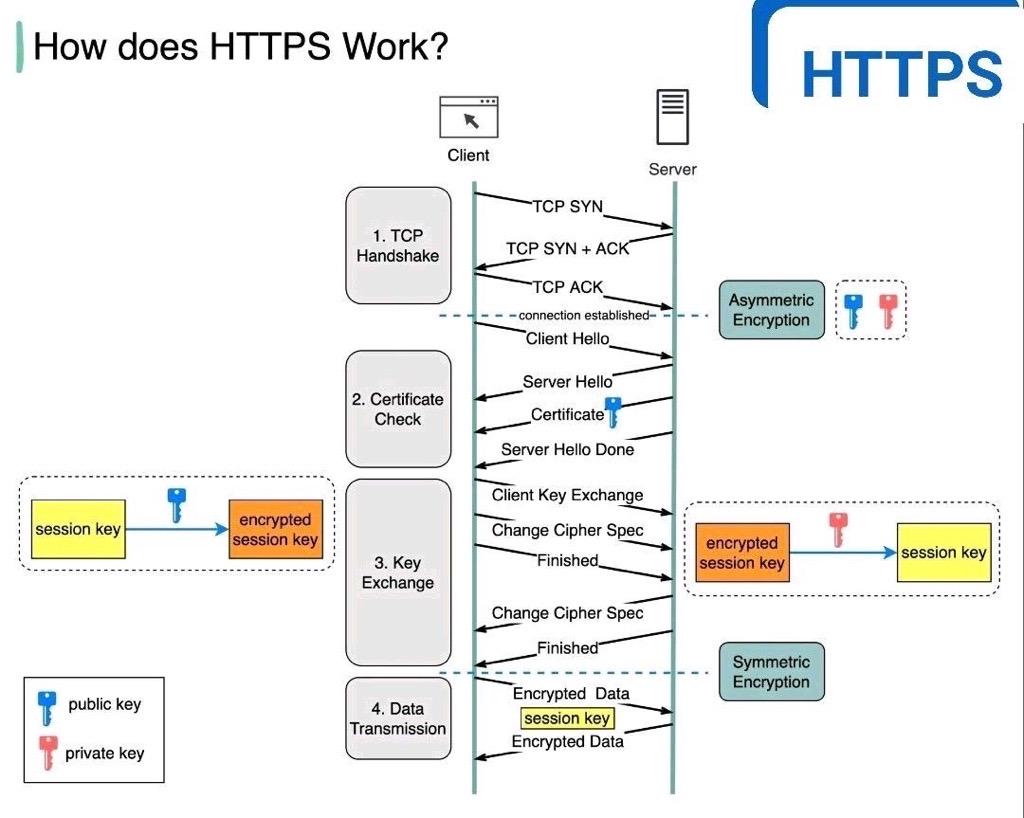
how https works?https工作原理
简单一句话: https http TLShttps 工作原理:HTTPS (Hypertext Transfer Protocol Secure)是一种带有安全性的通信协议,用于在互联网上传输信息。它通过使用加密来保护数据的隐私和完整性。下面是 HTTPS 的工作原理:初始化安全会…...

Docker的资源控制管理
目录 一、CPU控制 1、设置CPU使用率上限 2、设置CPU资源占用比(设置多个容器时才有效) 3、设置容器绑定指定的CPU 二、对内存使用进行限制 1、创建指定物理内存的容器 2、创建指定物理内存和swap的容器 3、 对磁盘IO配额控制(blkio&a…...

MMSeg无法使用单类自定义数据集训练
文章首发及后续更新:https://mwhls.top/4423.html,无图/无目录/格式错误/更多相关请至首发页查看。 新的更新内容请到mwhls.top查看。 欢迎提出任何疑问及批评,非常感谢! 摘要:将三通道图像转为一通道图像,…...

Redis使用方式
一、Redis基础部分: 1、redis介绍与安装比mysql快10倍以上 *****************redis适用场合**************** 1.取最新N个数据的操作 2.排行榜应用,取TOP N 操作 3.需要精确设定过期时间的应用 4.计数器应用 5.Uniq操作,获取某段时间所有数据排重值 6.实时系统,反垃圾系统7.P…...
 枪械名 红字效果 元素属性 清图评分 Boss战评分 泛用性评分 特殊性评分 最终评级 掉落点 掉率 图片 瘟疫传播)
无主之地3重型武器节奏评分榜(9.25) 枪械名 红字效果 元素属性 清图评分 Boss战评分 泛用性评分 特殊性评分 最终评级 掉落点 掉率 图片 瘟疫传播
无主之地3重型武器节奏评分榜(9.25) 枪械名 红字效果 元素属性 清图评分 Boss战评分 泛用性评分 特殊性评分 最终评级 掉落点 掉率 图片 瘟疫传播者 发射巨大能量球,能量球会额外生成追踪附近敌人的伴生弹 全属性 SSS SSS SSS - T0 伊甸6号-…...

什么是编程什么是算法
1.绪论 编程应在一个开发环境中完成源程序的编译和运行。首先,发现高级语言开发环境,TC,Windows系统的C++,R语言更适合数学专业的学生。然后学习掌握编程的方法,在学校学习,有时间的人可以在网上学习,或者购买教材自学。最后,编写源程序,并且在开发环境中实践。 例如…...

【c++】函数
文章目录函数的定义函数的调用值传递常见样式函数的声明函数的分文件编写函数的作用: 将一段经常使用的代码封装起来,减少重复代码。 一个较大的程序,一般分为若干个程序块,每个模板实现特定的功能。 函数的定义 返回值类型 函数…...

[golang gin框架] 1.Gin环境搭建,程序的热加载,路由GET,POST,PUT,DELETE
一.Gin 介绍Gin 是一个 Go (Golang) 编写的轻量级 http web 框架,运行速度非常快,如果你是性能和高效的追求者,推荐你使用 Gin 框架.Gin 最擅长的就是 Api 接口的高并发,如果项目的规模不大,业务相对简单,这…...
【开源】祁启云网络验证系统V1.11
简介 祁启云免费验证系统 一个使用golang语言、Web框架beego、前端Naive-Ui-Admin开发的免费网络验证系统 版本 当前版本1.11 更新方法 请直接将本目录中的verification.exe/verification直接覆盖到你服务器部署的目录,更新前,请先关闭正在运行的验…...

震源机制(Focal Mechanisms)之沙滩球(Bench Ball)
沙滩球包含如下信息: a - 判断断层类型,可根据球的颜色快速判断 b - 判断断层的走向(strike),倾角(dip) c - 确定滑移角/滑动角(rake) 走向 ,倾角,滑移角 如不了解断层的定义,可以先阅读:震…...

C++入门:多态
多态按字面的意思就是多种形态。当类之间存在层次结构,并且类之间是通过继承关联时,就会用到多态。C 多态意味着调用成员函数时,会根据调用函数的对象的类型来执行不同的函数。1、纯虚函数声明如下: virtual void funtion1()0; 纯…...
(C++实现))
华为OD真题_工位序列统计友好度最大值(100分)(C++实现)
题目描述 工位由序列F1,F2…Fn组成,Fi值为0、1或2。其中0代表空置,1代表有人,2代表障碍物。 1、某一空位的友好度为左右连续老员工数之和 2、为方便新员工学习求助,优先安排友好度高的空位 给出工位序列,求所有空位中友好度的最大值。 输入描述 第一行为工位序列:F1,F…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
