力扣第五十七题——插入区间
内容介绍
给你一个 无重叠的 ,按照区间起始端点排序的区间列表
intervals,其中intervals[i] = [starti, endi]表示第i个区间的开始和结束,并且intervals按照starti升序排列。同样给定一个区间newInterval = [start, end]表示另一个区间的开始和结束。在
intervals中插入区间newInterval,使得intervals依然按照starti升序排列,且区间之间不重叠(如果有必要的话,可以合并区间)。返回插入之后的
intervals。注意 你不需要原地修改
intervals。你可以创建一个新数组然后返回它。示例 1:
输入:intervals = [[1,3],[6,9]], newInterval = [2,5] 输出:[[1,5],[6,9]]示例 2:
输入:intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8] 输出:[[1,2],[3,10],[12,16]] 解释:这是因为新的区间[4,8]与[3,5],[6,7],[8,10]重叠。提示:
0 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 105intervals根据starti按 升序 排列newInterval.length == 20 <= start <= end <= 105
完整代码
int** insert(int** intervals, int intervalsSize, int* intervalsColSize, int* newInterval, int newIntervalSize, int* returnSize, int** returnColumnSizes) {*returnSize = 0;int left = newInterval[0];int right = newInterval[1];bool placed = false;int** ans = malloc(sizeof(int*) * (intervalsSize + 1));*returnColumnSizes = malloc(sizeof(int*) * (intervalsSize + 1));for (int i = 0; i < intervalsSize; ++i) {int* interval = intervals[i];if (interval[0] > right) {// 在插入区间的右侧且无交集if (!placed) {int* tmp = malloc(sizeof(int) * 2);tmp[0] = left, tmp[1] = right;(*returnColumnSizes)[*returnSize] = 2;ans[(*returnSize)++] = tmp;placed = true;}int* tmp = malloc(sizeof(int) * 2);memcpy(tmp, interval, sizeof(int) * 2);(*returnColumnSizes)[*returnSize] = 2;ans[(*returnSize)++] = tmp;} else if (interval[1] < left) {// 在插入区间的左侧且无交集int* tmp = malloc(sizeof(int) * 2);memcpy(tmp, interval, sizeof(int) * 2);(*returnColumnSizes)[*returnSize] = 2;ans[(*returnSize)++] = tmp;} else {// 与插入区间有交集,计算它们的并集left = fmin(left, interval[0]);right = fmax(right, interval[1]);}}if (!placed) {int* tmp = malloc(sizeof(int) * 2);tmp[0] = left, tmp[1] = right;(*returnColumnSizes)[*returnSize] = 2;ans[(*returnSize)++] = tmp;}return ans;
}
思路详解
一、问题背景
给定一个二维数组intervals,其中每个子数组表示一个区间,我们需要合并这些区间,使得没有重叠的区间尽可能紧密相连。同时,我们有一个新的区间newInterval,需要将其插入到intervals中。
二、解题思路
-
排序:
- 首先,我们需要对
intervals数组进行排序。排序的依据是每个子数组的第一个元素,因为合并的目的是让没有重叠的区间尽可能紧密相连。
- 首先,我们需要对
-
插入新区间:
- 创建一个
List<int[]>,用于存储合并后的区间。 - 遍历排序后的
intervals数组,对于每个区间,根据合并策略添加或更新列表中的区间。 - 同时,插入新区间
newInterval,根据新区间与当前区间的相对位置,决定是否需要更新列表中的区间。
- 创建一个
-
返回结果:
- 遍历完成后,将
List<int[]>转换为二维数组并返回。
- 遍历完成后,将
三、代码详解
- 排序:
- 使用
Arrays.sort方法对intervals数组进行排序,比较器比较的是每个子数组的第一个元素。
- 使用
Arrays.sort(intervals, new Comparator<int[]>() {public int compare(int[] interval1, int[] interval2) {return interval1[0] - interval2[0];}
});
- 插入新区间:
- 遍历排序后的
intervals数组,对于每个区间,根据合并策略添加或更新列表中的区间。 - 同时,插入新区间
newInterval,根据新区间与当前区间的相对位置,决定是否需要更新列表中的区间。
- 遍历排序后的
for (int i = 0; i < intervalsSize; ++i) {int* interval = intervals[i];if (interval[0] > right) {// 在插入区间的右侧且无交集if (!placed) {int* tmp = malloc(sizeof(int) * 2);tmp[0] = left, tmp[1] = right;(*returnColumnSizes)[*returnSize] = 2;ans[(*returnSize)++] = tmp;placed = true;}int* tmp = malloc(sizeof(int) * 2);memcpy(tmp, interval, sizeof(int) * 2);(*returnColumnSizes)[*returnSize] = 2;ans[(*returnSize)++] = tmp;} else if (interval[1] < left) {// 在插入区间的左侧且无交集int* tmp = malloc(sizeof(int) * 2);memcpy(tmp, interval, sizeof(int) * 2);(*returnColumnSizes)[*returnSize] = 2;ans[(*returnSize)++] = tmp;} else {// 与插入区间有交集,计算它们的并集left = fmin(left, interval[0]);right = fmax(right, interval[1]);}
}
- 返回结果:
- 遍历完成后,将
List<int[]>转换为二维数组并返回。
- 遍历完成后,将
return ans;
四、总结
通过上述步骤,我们能够有效地合并区间,并将新区间插入到区间列表中。关键在于正确地排序区间并合并它们。这种方法的时间复杂度为O(n log n),其中n是intervals数组的长度,因为排序操作的时间复杂度为O(n log n)。空间复杂度为O(n),用于存储合并后的区间。
知识点精炼
一、核心概念
- 排序算法:在解决组合问题时,排序可以帮助我们找到最优解或近似解。
- 动态规划:在某些情况下,我们可以通过动态规划来优化算法,减少重复计算。
- 二维数组:在处理与位置相关的数据时,二维数组是一个非常有用的数据结构。
二、知识点精炼
-
区间合并问题:
- 给定一个二维数组
intervals,其中每个子数组表示一个区间,需要合并这些区间,使得没有重叠的区间尽可能紧密相连。
- 给定一个二维数组
-
插入新区间:
- 创建一个
List<int[]>,用于存储合并后的区间。 - 遍历排序后的
intervals数组,对于每个区间,根据合并策略添加或更新列表中的区间。 - 同时,插入新区间
newInterval,根据新区间与当前区间的相对位置,决定是否需要更新列表中的区间。
- 创建一个
-
返回结果:
- 遍历完成后,将
List<int[]>转换为二维数组并返回。
- 遍历完成后,将
三、性能分析
- 时间复杂度:O(n log n),其中n是
intervals数组的长度,因为排序操作的时间复杂度为O(n log n)。 - 空间复杂度:O(n),用于存储合并后的区间。
四、实际应用
- 数据处理:在处理与位置相关的数据时,这种算法可以帮助我们合并区间,使得没有重叠的区间尽可能紧密相连。
- 算法竞赛:在算法竞赛中,掌握这种算法对于解决与区间合并相关的问题非常有帮助。
五、代码实现要点
- 排序:正确使用
Arrays.sort方法进行排序。 - 合并区间:正确实现合并策略,避免数组越界和重复添加。
- 返回结果:正确返回合并后的区间数组。
相关文章:

力扣第五十七题——插入区间
内容介绍 给你一个 无重叠的 ,按照区间起始端点排序的区间列表 intervals,其中 intervals[i] [starti, endi] 表示第 i 个区间的开始和结束,并且 intervals 按照 starti 升序排列。同样给定一个区间 newInterval [start, end] 表示另一个区…...

跟《经济学人》学英文:2024年08月03日这期 India’s economic policy will not make it rich
India’s economic policy will not make it rich A new World Bank report takes aim at emerging-market growth plans 原文: The developing world has fallen back in love with economic planning. As protectionism sweeps the West, poor countries are n…...

js 深拷贝、浅拷贝深度解析
赋值操作: let obj{a:1,b:[1,2,3],c:{m:2}}let newObjobjnewObj.a2newObj.b.push(4)newObj.c.m3console.log(obj,newObj); 将一个对象赋值给一个变量,其实就是将这个对象在栈内存中的引用地址复制给了这个变量,这两个对象指向堆内存中的同一个…...

CSS文本两端对齐
背景 如果我们要写了列表或表单类的样式,名称长短不一,但是想要两端对齐,如下面这样的: 你是怎么写的? 是这样的吗,在HTML里调整加空格: <ul><li>用户名</li><li>账 …...

C#中的foreach和自定义比较
在C#中foreach不能修改集合里面的值 在C#中,使用 foreach 循环遍历集合时,通常不建议修改集合中的元素,因为 foreach 循环是针对集合的枚举器进行操作的,而枚举器通常不支持修改集合中的元素。如果尝试在 foreach 循环中修改集合…...
有序转化数组(LeetCode)
题目 给你一个已经 排好序 的整数数组 和整数 、 、 。对于数组中的每一个元素 ,计算函数值 ,请 按升序返回数组 。 解题 在时间复杂度为解决问题 def sortTransformedArray(nums, a, b, c):def f(x):return a * x * x b * x cn len(nums)result…...

大数据信用报告查询有什么作用?怎么选择查询平台?
随着互联网的快速发展,人们的金融行为越来越多地依赖于网络平台。然而,网络上的金融交易存在着一定的风险,为了有效地防范这些风险,金融机构采用了大数据技术进行风险控制,下面,小易大数据平台将详细介绍大…...

import cv2ModuleNotFoundError: No module named ‘cv2‘
import cv2 ModuleNotFoundError: No module named cv2 (base) PS D:\CAMERA-D861T\LabelImg> pip3 install cv2 ERROR: Could not find a version that satisfies the requirement cv2 (from versions: none) ERROR: No matching distribution found for cv2 办法1 试了无…...

[Modbus] Modbus协议开发-基本概念(一)
历史 ModBus官网是Modicon(Modicon早年已被施耐德收购)公司为其PLC通讯而开发的一种通讯协议。 概述 通过Modbus协议,控制器之间、或控制器经由网络(如以太网)可以和其它设备之间进行通信。 优点 免费、好用、成熟…...

爬虫代理的使用:提升爬虫效率
爬虫代理的基本概念 爬虫代理,简单来说,就是位于客户端和目标服务器之间的一个中转站。当爬虫发起请求时,不是直接发送给目标服务器,而是先发送给代理服务器,再由代理服务器转发给目标服务器。目标服务器响应后&#…...

【gcc】基于gpt和python的流程和延迟梯度分析
Core Flow and Algorithm Concepts of GCC (Google Congestion Control) 【TWCC 】基于gpt和python简化分析webrtc拥塞控制论文: Analysis and Design of the Google Congestion Contro for Web Real-time Communication (WebRTC)参考大神的理解发送码率(send bitrate)影响了网…...

前端CSS总结
目录 前言 正文 CSS基础介绍: CSS选择器: 元素选择器: id和class选择器: 后代选择器和群组选择器: 盒子模型 content: padding: border: margin: 字体样式 …...

Linux/C 高级——指针函数
1.概念 本质是函数,函数的返回值为指针。类比着指针数组。 指针数组:本质是数组,数组中存放指针。 数据类型 *数组名[元素个数]; int a[2][3]; int *arr[2] {a[0],a[1]}; //*(*(arri)j) *(arr[i]j) arr[i][j] 2.定义格式 格式: 数…...
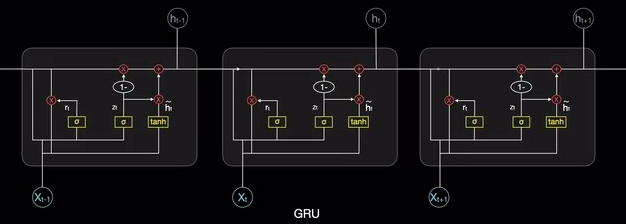
GRU门控循环单元【数学+图解】
文章目录 1、简介2、门控机制3、公式4、图解GRU4.1、重置门和更新门4.2、候选隐藏状态和隐藏状态⭐ 5、LSTM与GRU的对比6、应用7、训练技巧 🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习ÿ…...
、bellman_ford之判断负权回路)
代码随想录算法训练营第六十一天|Bellman_ford 队列优化算法(又名SPFA)、bellman_ford之判断负权回路
卡码网:94. 城市间货物运输 I from collections import dequeclass Edge:def __init__(self, to, val):self.to to # 链接的节点self.val val # 边的权重def main():n, m map(int, input().split())grid [list() for _ in range(n 1)] # 初始化邻接表for _…...
已完结)
ArrayList集合源码解读(二)已完结
ArrayList集合源码解读(二) 前言 这篇文章已经把 ArrayList 更完了。各位还想看什么源码可以私信我~~ 上节课带大家阅读了 ArrayList 中的核心扩容代码,那么今天带大家阅读下List集合中我们常用的几个方法的底层实现逻辑! 常用…...

光伏逆变器、MPPT、PCS储能变流器、BMU、BCU、BDU和液冷机组
一、光伏逆变器 光伏逆变器(PV inverter或solar inverter)可以将光伏(PV)太阳能板产生的可变直流电压转换为市电频率交流电(AC)的逆变器,可以反馈回商用输电系统,或是供离网的电网使…...

OpenHarmony编译
简介:本文将会介绍编译OpendHarmony环境的搭建、编译、和刷机(rk3568) 使用场景:修改系统源码,需要验证修改的功能是否正确、编译镜像、编译SDK 1、VS Code,下载链接,用于修改源码 2、linux环…...

C语言典型例题30
《C程序设计教程(第四版)——谭浩强》 习题2.7 从银行贷了一笔款d,准备每月还款额为p,月利率为r,计算多少个月能还清。 设d30000元,p6000元,r1%。对求得的月份取小数点后一位,对第二…...

springMVC @RestControllerAdvice注解使用方式
使用 RestControllerAdvice 的主要场景包括: 全局异常处理:处理所有控制器中抛出的未捕获异常。数据校验失败处理:处理 Bean Validation 校验失败的情况。自定义响应:统一定义响应格式或错误信息。 RestControllerAdvice 注解的…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
shellcode混淆uuid/ipv6/mac)
【免杀】C2免杀技术(十五)shellcode混淆uuid/ipv6/mac
针对 shellcode 混淆(Shellcode Obfuscation) 的实战手段还有很多,如下表所示: 类型举例目的编码 / 加密XOR、AES、RC4、Base64、Poly1305、UUID、IP/MAC改变字节特征,避开静态签名或 YARA结构伪装PE Stub、GIF/PNG 嵌入、RTF OLE、UUID、IP/MAC看起来像合法文件/数据,弱…...

Ansys Maxwell:线圈和磁体的静磁 3D 分析
本博客展示了如何在 Ansys Maxwell 中执行静磁 3D 分析,以计算载流线圈和永磁体之间相互作用产生的扭矩。在这个例子中,线圈中的电流产生一个沿 Y 轴指向的磁场,而永磁体沿 X 轴被磁化。这种配置导致围绕 Z 轴的扭矩。分步工作流程包括构建几…...
