XCPC第十一站,带你学会图论基本算法

我们约定:以下n表示点的数目,m表示边的数目。
引子1——邻接表存储图的方法()(暂时不考虑重边和自环)
现在我们有n个点(编号为1~n)和m条边,要用数组存储它们,我们可以怎么做呢?我们可以采取逐条加边的方法。假如我们要存储一条从a指向b的长度为w的边(注意,这里的a、b代表的是端点的具体编号而非端点被加入图中的次序号。为了不与下面的idx“编号”发生混淆,我们这里称a、b分别为加入的边的起点和终点的值)
const int K = ……(此处根据题目所给数据范围确定)
int h[K],e[K],ne[K],w[K],idx;
void add(int a,int b,int w)
{e[idx] = b;ne[idx] = h[a];w[idx] = w;h[a] = idx++;
}
//初始化
memset(h,-1,sizeof h);
以上便是经典的邻接表加边函数的代码。下面我们详尽解释各变量、数组和代码的含义。至于为什么它们的含义如此我们将在下面的模拟图中看出。
idx:编号(下文中的“编号”指的是在e数组中的编号,编号是几就是第几加一条被存进数组的边的终点的编号减1)。在最后的idx++执行完后,表示当前图中有idx条边,(idx+1)个点,下一条要加入的边(如果有的话)的终点在e数组中的下标为idx。
h数组:存储编号的数组。h[k]表示值为k的点指向的下一个点的编号x(如果有多个“下一个点”,则表示的是最后加入的那一个)。这里很多资料说h数组存储的是头节点,但实际上,h数组的下标的值并不总是某条路径的头,因此这种说法是不正确的。
w数组:存储边的长度。w[k]表示第(k+1)条被加入的边的长度
ne数组:虚拟指针数组。邻接表保证了每个节点(除头节点无出边外)都必定有入边和出边(若某个节点没有真正的出边,就让它指向-1)。ne[k]表示编号为k的点的下一个点的编号
e数组:存储值的数组。e[k]表示第(k+1)条加入的边的终点的值。
那么,我们自然可以推导出遍历所有边的代码——
for(int i = h[u];i!=-1;i = ne[i])
………………

引子2——邻接矩阵存储图
邻接矩阵存储图较为简单。我们开一个二维数组g,其中g[i][j]表示从值为i的点到值为j的点的距离。
一.朴素Dijkstra算法(适用于求解稠密图且所有边权威正的单源最短路问题,复杂度为O(n^2))

基本思想:循环n次,找到每个点到起点的最短距离,并且用已经更新过的点去更新未被更新的点。
#include<iostream>
#include<cstring>
using namespace std;const int N = 510;
//g[i][j]表示点i到点j的距离,dis[i]表示当前(注意是当前,未必是最小)第i个点到起点的最短距离
int g[N][N],dis[N],n,m;
//isConfirmed集合用于记录某点到起点距离的最小值是否已经被确定
bool isConfirmed[N];int Dijkstra()
{dis[1] = 0;//之所以要有最外层循环,是因为我们一共有n个点,每次我们只能找到一个不在isConfirmed集合里的且离起点最近的点,我们一共要找n个这样的点。i = k表示当前最短路径上一共有了k个点for(int i = 1;i<=n;i++){//t表示所有不在已经生成的路径中的点中离起点最近的点,初始时未确定,因此赋值-1int t = -1;//枚举所有点,找到不在isConfirmed集合中离起点最近的点赋予给tfor(int j = 1;j<=n;j++){if(!isConfirmed[j]&&(t==-1||dis[t]>dis[j])) t = j;}isConfirmed[t] = true;//找到不在isConfirmed集合中离起点最近的点后,用该点更新它所有相邻点到起点的最短距离for(int j = 1;j<=n;j++)dis[j] = min(dis[j],g[t][j]+dis[t]);}//不要直接返回无穷大,否则可能出现无法预料的后果//0x3f和0x3f3f3f3f不同,它们仅在用memset初始化时可以互换!if(dis[n]==0x3f3f3f) return -1;else return dis[n];
}int main()
{//刚开始所有点到起点的距离都还没有确定,因此赋值为正无穷memset(dis,0x3f,sizeof dis);cin>>n>>m;for(int i = 1;i<=n;i++){for(int j = 1;j<=n;j++){//处理自环if(i==j) g[i][j] = 0;else g[i][j] = 0x3f3f3f;}}while(m--){int x,y,z;cin>>x>>y>>z;//若存在重边,取最短边g[x][y] = min(g[x][y],z);}printf("%d",Dijkstra());return 0;
}
二.堆优化版的Dijkstra算法(适用于求解稀疏图且所有边权为正的单源最短路问题,复杂度为O(mlogn))
基本思想:在Dijkstra算法中有求不在isConfirmed集合中的到起点距离最短的点的操作,这一步可以用堆进行优化。

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 200000;
int h[N],e[N],ne[N],w[N],dis[N],idx,n,m;
//因为要存储编号和到起点的距离两个量,所以要用pair
typedef pair<int,int> PII;
bool isConfirmed[N];int add(int a,int b,int c)
{e[idx] = b;ne[idx] = h[a];//这里是w[idx]而非w[b],w[k]表示第k条边的长度w[idx] = c;h[a] = idx++;
}int Dijkstra()
{dis[1] = 0;//定义小根堆priority_queue<PII, vector<PII>, greater<PII>> heap; //把起点放进堆中//这个顺序不能倒。因为heap首先是根据距离排序而不是点的编号heap.push({0,1});//由于堆中存的是不在isConfirmed集合中的点,当堆不空,意味着还有没确定最短距离的点while(heap.size()){//取出堆顶,这就是当前不在isConfirmed集合中距离起点最近的点(这里的“距离”并不指最终的最短距离,而是更新到当前为止的最短距离)PII t = heap.top();heap.pop();int number = t.second;int distance = t.first;//这句话必不可少。因为若number这个点到起点的最短距离已经确定,我们再进行操作的话会导致复杂度增加.为了不爆TLE,我们应该在操作完毕后停止if(isConfirmed[number] == true) continue;isConfirmed[number] = true;//用当前不在isConfirmed集合中且离起点最近的点来更新它能到达的点到起点的最短距离for(int i = h[number];i!=-1;i = ne[i]){//得到当前点的编号int j = e[i];//如果j到起点的最短距离已经被确定,就不用继续做下去了if(!isConfirmed[j]&&dis[j]>distance+w[i]){dis[j] = distance+w[i];//在这一步,重边和自环被无形中处理掉了。若有重边,只有长度最短的那一条边对应的距离会进堆。heap.push({dis[j],j});//这里不能写isConfirmed[j] = true。因为j的“最短”只是暂时的,是当前已经生成的最短路径下到起点的最小值}}}if(dis[n]==0x3f3f3f3f) return -1;else return dis[n];
}int main()
{memset(dis,0x3f,sizeof dis);memset(h,-1,sizeof h);scanf("%d%d",&n,&m);while(m--){int x,y,z;scanf("%d%d%d",&x,&y,&z);add(x,y,z);}cout<<Dijkstra();return 0;
}三.Bellman_ford算法(适用于求解存在负权边或限制经过的边数的单源最短路问题,复杂度为O(nm))

#include<iostream>
#include<cstring>
using namespace std;
const int K = 10010;
//这里也可以用结构体数组存
int backup[K],dist[K],n,m,k;struct Edge
{int a,b,w;
}edges[K];bool bellman_ford()
{memset(dist,0x3f,sizeof dist);dist[1] = 0;for(int i = 1;i<=k;i++){memcpy(backup,dist,sizeof dist);//这里j开始的下标要和main函数中i开始的下标相同,这样才访问到edges数组的同一个地方for(int j = 1;j<=m;j++)//遍历所有边,每条边终点到源点的最短距离等于该点到源点的直接距离与该边起点到源点的最短距离和该边长度的和的较小值//j是编号不是值,这样恰好符合dist数组的定义。dist[k]表示编号为k(这里的编号指的是该点第几个被插入)的点到源点的最短距离。edges[j].w指的是跟第j个出现(被输入)的点相连的边的长度dist[edges[j].b] = min(dist[edges[j].b],backup[edges[j].a]+edges[j].w);}//这里由于可能出现负权边,导致dist[n]被更新成比0x3f3f3f3f小一点的数,但是又不会小太多,所以我们改为dist[n]比某个较大的数大就可以认为它是正无穷了。if(dist[n]>0x3f3f3f/2) return false;else return true;
}int main()
{cin>>n>>m>>k;for(int i = 1;i<=m;i++)cin>>edges[i].a>>edges[i].b>>edges[i].w;if(!bellman_ford()) cout<<"impossible";else cout<<dist[n];return 0;
}
四.spfa算法(Bellman_ford的优化版。一般情况下复杂度为O(m),最坏为O(nm))

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int K = 100010;
int h[K],e[K],ne[K],w[K],dist[K],n,m,idx;
bool isInQueue[K];void add(int a,int b,int c)
{e[idx] = b;ne[idx] = h[a];w[idx] = c;h[a] = idx++;
}bool spfa()
{memset(dist,0x3f,sizeof dist);dist[1] = 0;//队列用于存储可以更新别的距离的点queue<int> q;q.push(1);isInQueue[1] = true;//当队列不空,说明我们还有材料更新别的点,说明我们的最短距离未全部确定while(q.size()){int t = q.front();q.pop();isInQueue[t] = false;for(int i = h[t];i!=-1;i = ne[i]){int j = e[i];if(dist[j]>dist[t]+w[i]){dist[j] = dist[t]+w[i];if(!isInQueue[j]){q.push(j);isInQueue[j] = true;}}}}if(dist[n] > 0x3f3f3f3f/2) return false;else return true;}int main()
{memset(h,-1,sizeof h);cin>>n>>m;while(m--){int x,y,z;cin>>x>>y>>z;add(x,y,z);}if(!spfa()) puts("impossible");else cout<<dist[n];return 0;
}五.floyd算法(求解多源头最短路问题)

#include<iostream>
using namespace std;
const int N = 210,M = 20010;
int g[N][N],n,m,k;void floyd()
{for(int k = 1;k<=n;k++)for(int i = 1;i<=n;i++)for(int j = 1;j<=n;j++)g[i][j] = min(g[i][j],g[i][k]+g[k][j]);
}int main()
{cin>>n>>m>>k;for(int i = 1;i<=n;i++){for(int j = 1;j<=n;j++){if(i==j) g[i][j] = 0;else g[i][j] = 0x3f3f3f3f;}}while(m--){int x,y,z;cin>>x>>y>>z;g[x][y] = min(g[x][y],z);}floyd();while(k--){int x,y;cin>>x>>y;if(g[x][y]>0x3f3f3f3f/2) cout<<"impossible"<<endl;else cout<<g[x][y]<<endl;}return 0;}
六.Prim算法(用于求最小生成树,复杂度O(n^2))

最小生成树是怎么生成的呢?我们看下面一个图就明白了。
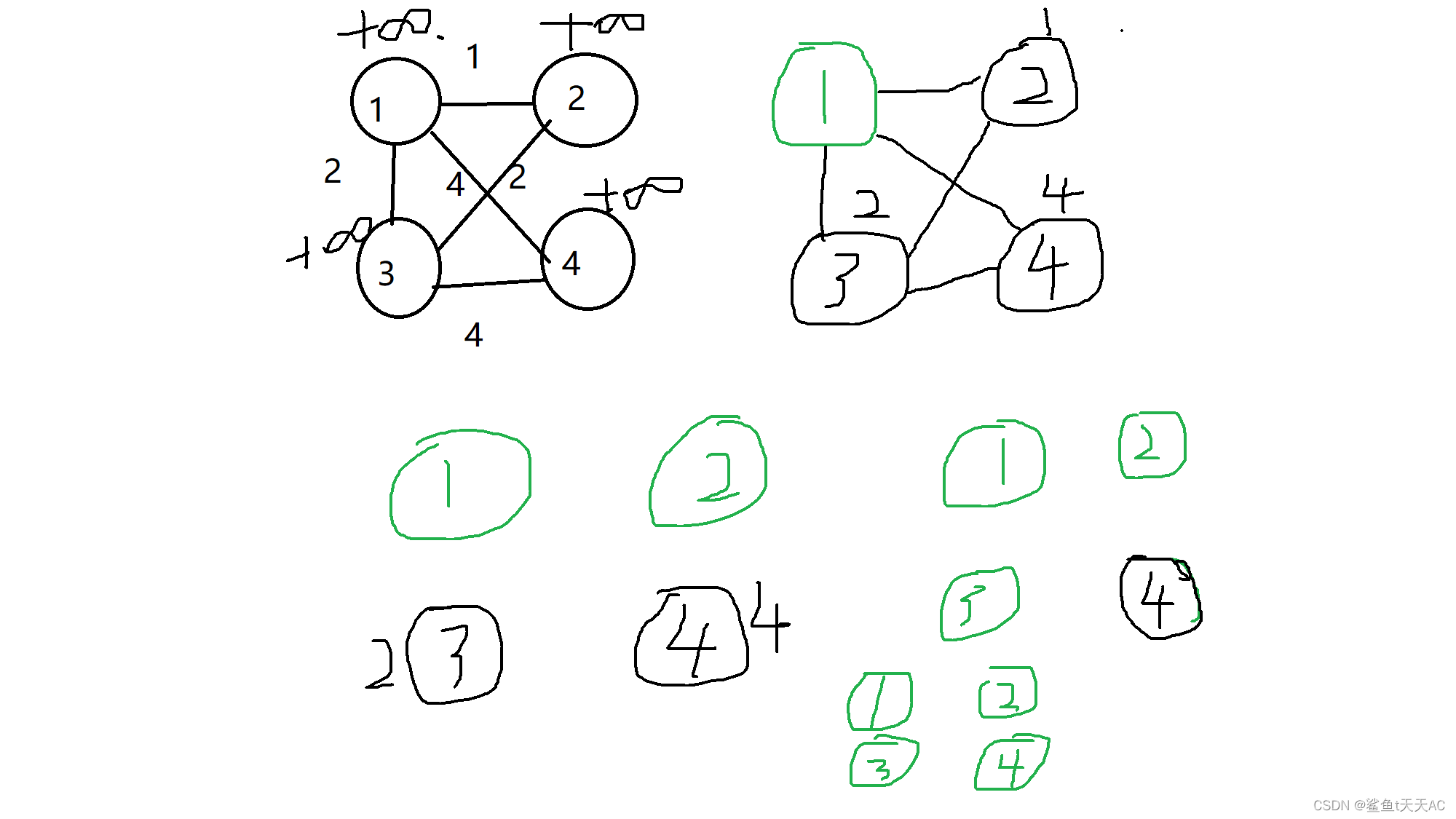
我们用S表示所有在已有连通块(即生成树)中的点构成的集合。最开始还没有生成树,点1、2、3、4到连通块的距离均为正无穷。然后选取一个距离已有连通块(这时为空)最近(这时1、2、3、4都是正无穷,一样近,那就选1好了)的点加入到连通块中,并用这个点更新其它在连通块外的点到连通块的距离。(某点到连通块的距离定义为该点到连通块中所有点的距离的最小值)以此类推,我们可以得到最小生成树。Prim算法的想法与Dijkstra类似,循环n次,每次找到不在连通块中且离连通块最近的点。具体的代码实现如下——
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510;
//因为边的数量较多(~N^2),这里我们用邻接矩阵来存储图
int g[N][N],dist[N],n,m,res;
bool isInTree[N];
int prim()
{memset(dist,0x3f,sizeof dist);//这里不能初始化dist[1]为0.因为此时还没有连通块,dist[1]也应该被看作正无穷//尽可能把所有点都包进连通块中for(int i = 0;i<n;i++){int t = -1;//找到当前不在连通块中离连通块最近的点for(int j = 1;j<=n;j++)if(!isInTree[j]&&(t==-1||dist[t]>dist[j])) t = j;//如果此时找到的最短距离都是无穷大,那么说明此时剩下的所有点根连通块都是不连通的,就返回正无穷表示不存在生成树//如果找到的不是第一个点(第一个点编号为0)而且到已有连通块的距离为正无穷,说明不连通。为什么要排除第一个点呢?因为第一个点到已有连通块的距离本来就应该是负无穷,因为彼时还没有连通块。if(i&&dist[t]==0x3f3f3f3f) return 0x3f3f3f3f;if(i) res+=dist[t];isInTree[t] = true;//遍历t的所有邻边,用这个找到的离连通块最近的点更新其它点到连通块的距离for(int j = 1;j<=n;j++)//这里不需要像Dijkstra那样再加上dist[t],因为dist[i]表示第i个点到已有连通块的距离而非源点的距离。既然t已经在连通块中,那么只要取dist[i]和个g[t][j]中的较小值即可dist[j] = min(dist[j],g[t][j]);}return res;
}int main()
{//先输入再初始化!!!!!!cin>>n>>m;for(int i = 1;i<=n;i++){for(int j = 1;j<=n;j++){if(i==j) g[i][j] = 0;else g[i][j] = 0x3f3f3f3f;}}while(m--){int u,v,w;cin>>u>>v>>w;g[u][v] = g[v][u] = min(g[u][v],w);}int l = prim();if(l==0x3f3f3f3f) puts("impossible");else cout<<l;return 0;
}
七.Kruskal算法(用于求最小生成树,复杂度O(mlogn))
Kruskal算法的想法很简单,就是将所有边按照边长从小到大排序,然后再枚举每条边即可。
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 100010, M = 200010, INF = 0x3f3f3f3f;int n, m;
int p[N];
//用结构体存储所有边和点即可,不用邻接表或邻接矩阵
struct Edge
{int a, b, w;
//重载小于号,按照边的长度将所有边排序bool operator< (const Edge &W)const{return w < W.w;}
}edges[M];
//并查集模板,寻找祖宗节点
int find(int x)
{if (p[x] != x) p[x] = find(p[x]);return p[x];
}int kruskal()
{//按照边的长度将所有边排序sort(edges, edges + m);for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
//res表示所有边的长度之和int res = 0, cnt = 0;//从小到大枚举每条边for (int i = 0; i < m; i ++ ){int a = edges[i].a, b = edges[i].b, w = edges[i].w;
//如果a和b的祖宗节点不同,说明不在同一个连通块中,这时候就把它们连起来
//cnt表示当前生成树中边的条数a = find(a), b = find(b);if (a != b){p[a] = b;res += w;cnt ++ ;}}if (cnt < n - 1) return INF;return res;
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < m; i ++ ){int a, b, w;scanf("%d%d%d", &a, &b, &w);edges[i] = {a, b, w};}int t = kruskal();if (t == INF) puts("impossible");else printf("%d\n", t);return 0;
}
相关文章:

XCPC第十一站,带你学会图论基本算法
我们约定:以下n表示点的数目,m表示边的数目。 引子1——邻接表存储图的方法()(暂时不考虑重边和自环) 现在我们有n个点(编号为1~n)和m条边,要用数组存储它们,…...
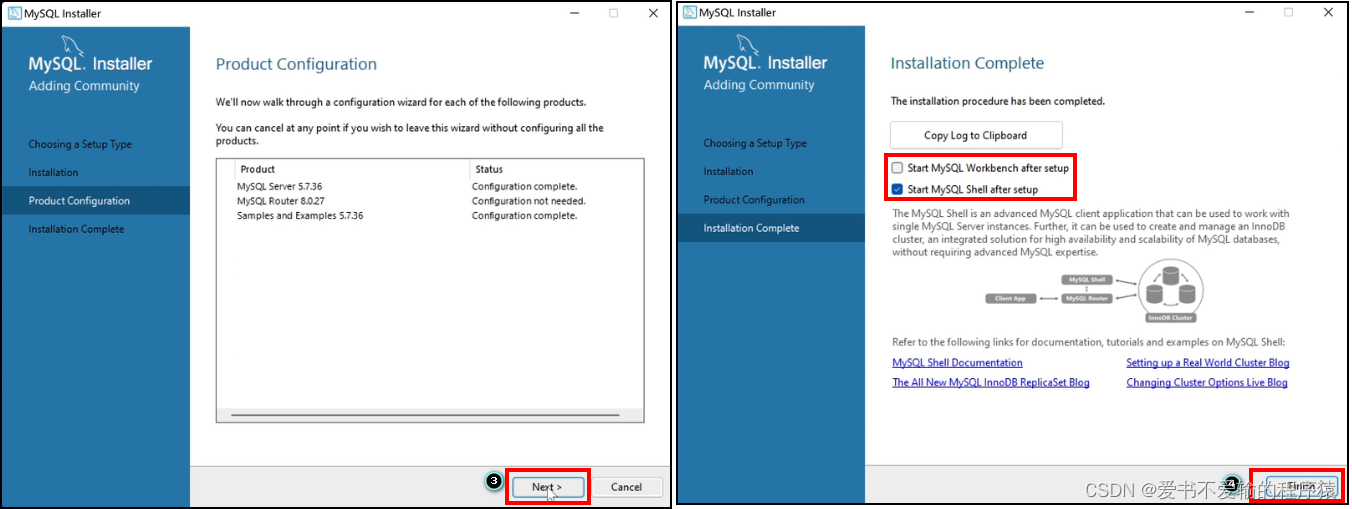
【MySQL】1 MySQL的下载、安装与配置|提供安装包
欢迎来到爱书不爱输的程序猿的博客, 本博客致力于知识分享,与更多的人进行学习交流 目前,已开了以下专栏,欢迎关注与指导 1️⃣Java基础知识系统学习(持续更文中…) 2️⃣UML(已更完) 3️⃣MySQL(持续更文中…) MYSQL的下载、安装与配置1.下载MySQL5.71.1安装包的获…...

Redis 事务
目录Redis 事务一、Redis事务的概念:二、redis事务提出的逻辑:三、redis事务的基本操作四、事务的执行流程五、redis锁六、redis分布式锁Redis 事务 一、Redis事务的概念: Redis 事务的本质是一组命令的集合。事务支持一次执行多个命令&…...

【linux】:进程控制
文章目录 前言一、什么是写时拷贝二、进程控制 1.进程终止2.进程等待三丶进程程序替换总结前言 了解上一篇文章中的进程地址空间后,我们再来说说进程控制的概念,进程控制我们需要搞清楚三个问题:如何进程终止,如何解决僵尸进程问…...
在recyclerview中使用其item布局的ViewBinding类需要注意的问题
问题描述 最近在使用RecycerView的瀑布流布局,我想直接用ViewBinding取得item中的一个TextView然后根据position进行赋值。 比如我点击测试标题2,它在日志中应该能打印出测试标题2才对。 但是他却打印出“测试标题0” 按理来说标题应该更点击的位置对…...

基于EB工具的TC3xx_MCAL配置开发05_ADC模块硬件Pwm触发Demo配置
目录 1.概述2. Pwm相关配置2.1 PWM->General配置2.2 PWM->PwmChannel配置2.2.1 Reference Pwm通道配置2.2.2 触发ADC采集的Pwm通道配置3. ADC相关配置3.1 AdcHwExtTrigSelect配置4. MCU相关配置4.1 GTM配置4.1.1 McuGtmTomAllocationConf配置4.1.2 GtmTriggerForAdc配置1…...

Qt示例3:用Qt画一个温度计
示例1 以下是用Qt绘制一个简单的温度计的示例代码: #include <QPainter> #include <QWidget> #include <QApplication> class Thermometer : public QWidget { public:Thermometer(QWidget *parent 0); protected:void paintEvent(QPaintEvent …...
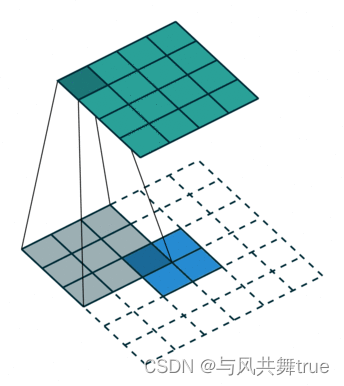
全卷积网络FCN
这里写目录标题全卷积网络FCN1、FCN2、FCN上采样3、 FCN具体实现过程转置卷积全卷积网络FCN 引用:http://t.csdn.cn/pDcjL 1、FCN FCN: FCN是对图像进行像素级的分类(也就是每个像素点都进行分类),从而解决了语义级别的图像分割…...

【Linux】基础IO流(上)
文章目录1. 预备知识2. 回忆C接口fopenfputsfprintfsnprintf追加方式—— a以读方式—— r3.操作系统如何进行读写文件操作open操作系统是如何让用户给自己传递标志位的理解标记位的问题新创建文件权限不正确解决 umask的权限write默认不会对原始文件清空系统层面追加系统层面 …...
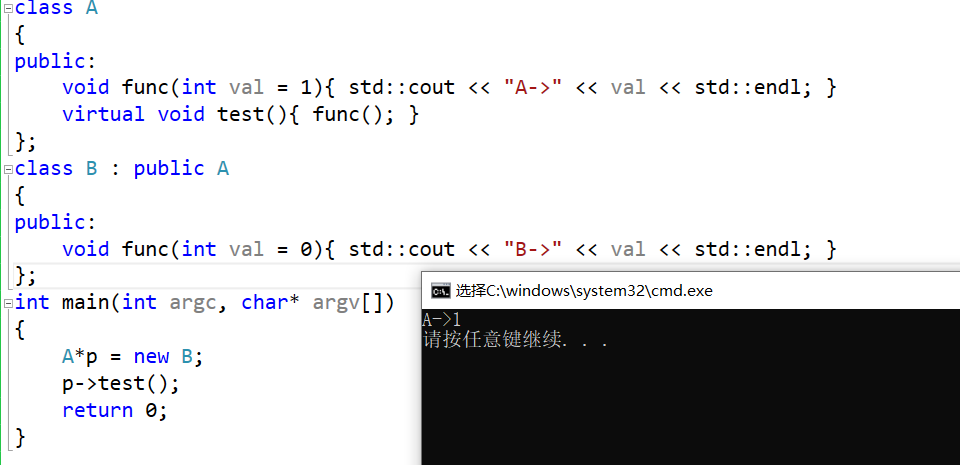
【C++】类和对象三大特性--多态
文章目录1. 多态的基本概念2. 多态的定义及实现2.1多态的构成条件2.2 虚函数2.3虚函数的重写2.4 虚函数不能重写和检查是否重写 (C11 )2.5 重载、覆盖(重写)、隐藏(重定义)的对比3. 纯虚函数和抽象类3.1 概念3.2 接口继承和实现继承4.多态的实现原理4.1虚…...

【微前端】qiankun + vite + vue3
专栏: 【微前端】什么是微前端【微前端】qiankun【微前端】qiankun vite vue3 一、整体结构 在 qiankun 体系下,一个微前端工程包含一个主应用和多个子应用。本质上,每个工程(主应用)都可以单独开发、运行。 1.1…...

模型部署之TorchScript
一.关于torchscript和jit介绍 1.关于torchscript TorchScript是Pytorch模型(继承自nn.Module)的中间表示,保存后的torchscript模型可以在像C这种高性能的环境中运行 TorchScript是一种从PyTorch代码创建可序列化和可优化模型的方法。任何T…...
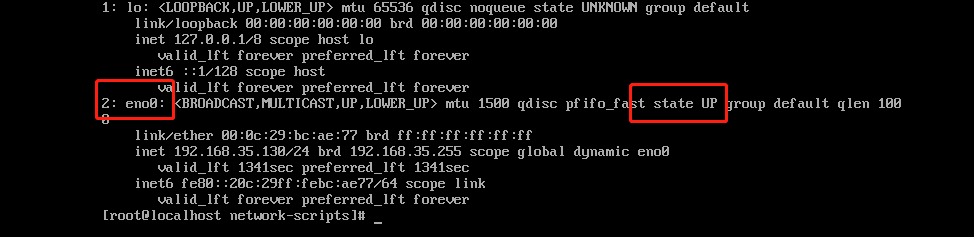
修改linux网卡配置文件的文件名
修改linux网卡配置文件的文件名 查看自己系统中网卡配置文件的文件名 #查看网卡的配置文件名,已经网络的状态 ip a查看系统是否可以使用ifconfig命令 #输入命令 ifconfig #出现以下图片表示ifconfig的命令可用。可能出现的错误:ifconfig command no foun…...

年轻人为啥热衷去寺庙?
年轻人的苦,寺庙最清楚。 周末的寺庙挤满了年轻人,北京雍和宫限流了,杭州灵隐寺十八籽的手串限购了,南京鸡鸣寺从地铁站出口就开始排队了...... “上班和上学,你选择哪个?” ”我选择上香“ 工作和学习…...

Java Spring 框架
当今世界,Java Spring 成为了最流行的 Java 开发框架之一。Spring 框架是一个轻量级的、高效的框架,它是 Java 应用程序开发的理想选择。在本文中,我们将深入探讨 Java Spring 框架的特性、优点以及如何使用它来构建高质量的应用程序。 1.Ja…...

基于OpenCV的人脸识别
目录 🥩 前言 🍖 环境使用 🍖 模块使用 🍖 模块介绍 🍖 模块安装问题: 🥩 OpenCV 简介 🍖 安装 OpenCV 模块 🥩 OpenCV 基本使用 🍖 读取图片 🍗 【…...

一文带你看懂电压放大器和功率放大器的区别
很多人对于电压放大器和功率放大器总是分不太清,在实际应用过程中,电压放大器和功率放大器所起到的作用都是相同的。对于功率放大器和电压放大器的区别,今天就让安泰电子来带我们一起看看。功率放大器和电压放大器的主要区别是:功…...
C++虚函数与多态
C虚函数与多态虚函数抽象类纯虚函数虚析构函数多态虚函数的几个问题纯虚函数和ADT虚函数 virtual修饰的成员函数就是虚函数, 1.虚函数对类的内存影响:增加一个指针类型大小(32位和64位) 2.无论有多少个虚函数,只增加一…...

蓝桥杯Web前端练习-----渐变色背景生成器
介绍 相信做过前端开发的小伙伴们对渐变色在 UI 设计中的流行度一定不陌生,网页上也时常可以看到各类复杂的渐变色生成工具。使用原生的 CSS 变量加一些 JS 函数就能做出一个简单的渐变色背景生成器。 现在渐变色生成器只完成了颜色选取的功能,需要大家…...

Python中的微型巨人-Flask
文章目录前言主要内容优点及特性主要使用创建实例定义路由获取请求定制响应渲染Jinja2模板重定向和反向解析抛出HTTP异常总结更多宝藏前言 😎🥳😎🤠😮🤖🙈💭🍳…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...

中国政务数据安全建设细化及市场需求分析
(基于新《政务数据共享条例》及相关法规) 一、引言 近年来,中国政府高度重视数字政府建设和数据要素市场化配置改革。《政务数据共享条例》(以下简称“《共享条例》”)的发布,与《中华人民共和国数据安全法》(以下简称“《数据安全法》”)、《中华人民共和国个人信息…...

DriveGPT4: Interpretable End-to-end Autonomous Driving via Large Language Model
一、研究背景与创新点 (一)现有方法的局限性 当前智驾系统面临两大核心挑战:一是长尾问题,即系统在遇到新场景时可能失效,例如突发交通状况或非常规道路环境;二是可解释性问题,传统方法无法解释智驾系统的决策过程,用户难以理解车辆行为的依据。传统语言模型(如 BERT…...

如何在Spring Boot中使用注解动态切换实现
还在用冗长的if-else或switch语句管理多个服务实现? 相信不少Spring Boot开发者都遇到过这样的场景:需要根据不同条件动态选择不同的服务实现。 如果告诉你可以完全摆脱条件判断,让Spring自动选择合适的实现——只需要一个注解,你是否感兴趣? 本文将详细介绍这种优雅的…...

Pycharm的终端无法使用Anaconda命令行问题详细解决教程
很多初学者在Windows系统上安装了Anaconda后,在PyCharm终端中运行Conda命令时,会遇到以下错误: conda : 无法将“conda”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。 请检查名称的拼写,如果包括路径,请确保…...
