002 | 常见的金融量化指标计算
金融量化指标
在金融量化分析中,常用的指标可以帮助我们判断市场走势、评估风险和收益,以及构建交易策略。以下是一些常见的金融量化指标及其计算方法的详细教程,包括公式与Python代码实现。
1. 移动平均线(Moving Average, MA)
简介:移动平均线是对特定时期内的数据进行平均,以平滑价格波动,从而帮助识别趋势方向。
公式:
M A n = P 1 + P 2 + . . . + P n n MA_n = \frac{P_1 + P_2 + ... + P_n}{n} MAn=nP1+P2+...+Pn
其中, P i P_i Pi 是第 i i i天的收盘价, n n n 是移动平均的周期。
Python代码:
import pandas as pddef moving_average(prices, window):return prices.rolling(window=window).mean()# 示例
data = pd.Series([100, 102, 101, 104, 106, 108])
ma = moving_average(data, 3)
print(ma)
2. 指数平滑移动平均线(Exponential Moving Average, EMA)
简介:EMA对最近的数据赋予更大的权重,从而比简单移动平均线更快地响应价格变化。
公式:
E M A t = α × P t + ( 1 − α ) × E M A t − 1 EMA_t = \alpha \times P_t + (1 - \alpha) \times EMA_{t-1} EMAt=α×Pt+(1−α)×EMAt−1
其中, α = 2 n + 1 \alpha = \frac{2}{n+1} α=n+12, n n n 是平滑周期。
Python代码:
def exponential_moving_average(prices, window):return prices.ewm(span=window, adjust=False).mean()# 示例
ema = exponential_moving_average(data, 3)
print(ema)
3. 相对强弱指数(Relative Strength Index, RSI)
简介:RSI衡量股票价格的上涨和下跌的速度,用于判断市场是否超买或超卖。
公式:
R S I = 100 − 100 1 + R S RSI = 100 - \frac{100}{1 + RS} RSI=100−1+RS100
其中,(RS = \frac{\text{平均上涨值}}{\text{平均下跌值}})。
Python代码:
def relative_strength_index(prices, window=14):delta = prices.diff()gain = (delta.where(delta > 0, 0)).rolling(window=window).mean()loss = (-delta.where(delta < 0, 0)).rolling(window=window).mean()rs = gain / lossrsi = 100 - (100 / (1 + rs))return rsi# 示例
rsi = relative_strength_index(data, 14)
print(rsi)
4. 移动平均收敛散度(Moving Average Convergence Divergence, MACD)
简介:MACD是两条指数移动平均线之间的差值,用于判断价格走势的变化趋势。
公式:
M A C D = E M A 12 − E M A 26 MACD = EMA_{12} - EMA_{26} MACD=EMA12−EMA26
S i g n a l = E M A 9 ( M A C D ) Signal = EMA_{9}(MACD) Signal=EMA9(MACD)
Python代码:
def macd(prices, short_window=12, long_window=26, signal_window=9):ema_short = exponential_moving_average(prices, short_window)ema_long = exponential_moving_average(prices, long_window)macd_line = ema_short - ema_longsignal_line = exponential_moving_average(macd_line, signal_window)return macd_line, signal_line# 示例
macd_line, signal_line = macd(data)
print(macd_line, signal_line)
5. 布林带(Bollinger Bands)
简介:布林带由三条线组成,中间的线是移动平均线,上下两条线分别是移动平均线加减一定倍数的标准差,用于衡量价格的波动范围。
公式:
上轨 = M A + k × σ \text{上轨} = MA + k \times \sigma 上轨=MA+k×σ
下轨 = M A − k × σ \text{下轨} = MA - k \times \sigma 下轨=MA−k×σ
其中, M A MA MA 是移动平均线, σ \sigma σ 是价格的标准差, k k k 是调整因子,一般取2。
Python代码:
def bollinger_bands(prices, window=20, num_std_dev=2):ma = moving_average(prices, window)std_dev = prices.rolling(window=window).std()upper_band = ma + num_std_dev * std_devlower_band = ma - num_std_dev * std_devreturn upper_band, lower_band# 示例
upper_band, lower_band = bollinger_bands(data)
print(upper_band, lower_band)
6. 平均真实波动范围(Average True Range, ATR)
简介:ATR用于衡量市场的波动性,反映了价格波动的剧烈程度。
公式:
T R = max ( 当前最高价 − 当前最低价 , ∣ 当前最高价 − 前一收盘价 ∣ , ∣ 当前最低价 − 前一收盘价 ∣ ) TR = \max(\text{当前最高价} - \text{当前最低价}, |\text{当前最高价} - \text{前一收盘价}|, |\text{当前最低价} - \text{前一收盘价}|) TR=max(当前最高价−当前最低价,∣当前最高价−前一收盘价∣,∣当前最低价−前一收盘价∣)
A T R = ∑ i = 1 n T R i n ATR = \frac{\sum_{i=1}^{n} TR_i}{n} ATR=n∑i=1nTRi
Python代码:
def true_range(high, low, close):return pd.concat([high - low, (high - close.shift()).abs(), (low - close.shift()).abs()], axis=1).max(axis=1)def average_true_range(high, low, close, window=14):tr = true_range(high, low, close)atr = tr.rolling(window=window).mean()return atr# 示例
high = pd.Series([105, 107, 110, 112])
low = pd.Series([100, 102, 104, 109])
close = pd.Series([102, 106, 108, 111])
atr = average_true_range(high, low, close)
print(atr)
7. 威廉指标(Williams %R)
简介:威廉指标用于判断市场的超买或超卖状态,数值范围在-100到0之间。
公式:
% R = 最高价 n − 收盘价 最高价 n − 最低价 n × ( − 100 ) \%R = \frac{\text{最高价}_n - \text{收盘价}}{\text{最高价}_n - \text{最低价}_n} \times (-100) %R=最高价n−最低价n最高价n−收盘价×(−100)
其中, 最高价 n \text{最高价}_n 最高价n 和 最低价 n \text{最低价}_n 最低价n 分别为过去n天内的最高和最低价格。
Python代码:
def williams_r(high, low, close, window=14):highest_high = high.rolling(window=window).max()lowest_low = low.rolling(window=window).min()wr = (highest_high - close) / (highest_high - lowest_low) * -100return wr# 示例
wr = williams_r(high, low, close)
print(wr)
8. 随机指标(Stochastic Oscillator)
简介:随机指标用于衡量收盘价在最近一段时间价格范围内的位置,判断价格的超买或超卖情况。
公式:
K = 收盘价 − 最低价 n 最高价 n − 最低价 n × 100 K = \frac{\text{收盘价} - \text{最低价}_n}{\text{最高价}_n - \text{最低价}_n} \times 100 K=最高价n−最低价n收盘价−最低价n×100
D = ∑ K 3 D = \frac{\sum K}{3} D=3∑K
Python代码:
def stochastic_oscillator(high, low, close, window=14):lowest_low = low.rolling(window=window).min()highest_high = high.rolling(window=window).max()k = (close - lowest_low) / (highest_high - lowest_low) * 100d = k.rolling(window=3).mean()return k, d# 示例
k, d = stochastic_oscillator(high, low, close)
print(k, d)
9. 平滑异同平均指标(Smoothed Moving Average, SMA)
简介:SMA是将移动平均和当前价格进行平滑处理的指标,比EMA更加平滑。
公式:
S M A t = ∑ i = 1 n P i n SMA_t = \frac{\sum_{i=1}^{n} P_i}{n} SMAt=n∑i=1nPi
其中, P i P_i Pi 是价格数据, n n n 是时间周期。
Python代码:
def smoothed_moving_average(prices, window):return prices.rolling(window=window).mean()# 示例
sma = smoothed_moving_average(data, 3)
print(sma)
10. 波动率(Volatility)
简介:波动率是衡量价格变化的剧烈程度的重要指标,通常用标准差表示。
公式:
Volatility = ∑ i = 1 n ( P i − M A ) 2 n \text{Volatility} = \sqrt{\frac{\sum_{i=1}^{n} (P_i - MA)^2}{n}} Volatility=n∑i=1n(Pi−MA)2
Python代码:
def volatility(prices, window):return prices.rolling(window=window).std()# 示例
vol = volatility(data, 10)
print(vol)
11. 商品通道指数(Commodity Channel Index, CCI)
简介:CCI衡量价格相对于其均值的偏离程度,用于判断市场的超买或超卖状态。
公式:
C C I = P t − M A t 0.015 × M D CCI = \frac{P_t - MA_t}{0.015 \times MD} CCI=0.015×MDPt−MAt
其中,(P_t) 是典型价格,(MA_t) 是移动平均,(MD) 是均方差。
Python代码:
def commodity_channel_index(high, low, close, window=20):tp = (high + low + close) / 3ma = tp.rolling(window=window).mean()md = tp.rolling(window=window).apply(lambda x: pd.Series(x).mad())cci = (tp - ma) / (0.015 * md)return cci# 示例
cci = commodity_channel_index(high, low, close)
print(cci)
12. 恐慌指数(VIX)
简介:VIX是衡量市场对未来30天价格波动预期的指标,通常被称为“恐慌指数”。
公式:VIX的计算比较复杂,通常基于标普500指数期权的隐含波动率来计算。它的公式涉及多个期权的计算,这里简化为波动率的代表。
Python代码:
import numpy as npdef vix(prices):log_returns = np.log(prices / prices.shift(1))vol = log_returns.rolling(window=30).std() * np.sqrt(252)return vol# 示例
vix_index = vix(data)
print(vix_index)
13. 收益率(Rate of Return, RoR)
简介:收益率是衡量投资或资产在特定时间内的增长或减少百分比。它通常用来评估投资的盈利能力。
公式:
-
简单收益率:
Simple Return = P t − P t − 1 P t − 1 × 100 % \text{Simple Return} = \frac{P_t - P_{t-1}}{P_{t-1}} \times 100\% Simple Return=Pt−1Pt−Pt−1×100%
其中,(P_t) 是当前价格,(P_{t-1}) 是前一时间点的价格。 -
对数收益率:
Log Return = ln ( P t P t − 1 ) \text{Log Return} = \ln\left(\frac{P_t}{P_{t-1}}\right) Log Return=ln(Pt−1Pt)
Python代码:
import numpy as npdef simple_return(prices):return (prices / prices.shift(1)) - 1def log_return(prices):return np.log(prices / prices.shift(1))# 示例
simple_r = simple_return(data)
log_r = log_return(data)
print(simple_r, log_r)
使用 Tushare 计算所有指标的综合示例
Tushare 是一个用于获取中国市场数据的开源Python包。我们将使用 Tushare 下载股票数据并计算上面介绍的指标。
1. 安装 Tushare
如果你还没有安装 Tushare,可以使用以下命令进行安装:
pip install tushare
2. 获取股票数据
首先,我们需要获取股票的历史价格数据。
import tushare as ts
import pandas as pd# 设置你的 Tushare token
ts.set_token('your_token_here')
pro = ts.pro_api()# 获取某只股票的日线数据
data = pro.daily(ts_code='000001.SZ', start_date='20220101', end_date='20221231')# 将数据按日期排序并设置日期为索引
data['trade_date'] = pd.to_datetime(data['trade_date'])
data = data.sort_values(by='trade_date')
data.set_index('trade_date', inplace=True)# 提取收盘价、高低价等数据
close = data['close']
high = data['high']
low = data['low']
3. 计算所有指标
我们将结合之前编写的函数,计算所有的指标:
# 移动平均线
ma_20 = moving_average(close, 20)# 指数平滑移动平均线
ema_20 = exponential_moving_average(close, 20)# 相对强弱指数
rsi_14 = relative_strength_index(close, 14)# 移动平均收敛散度
macd_line, signal_line = macd(close)# 布林带
upper_band, lower_band = bollinger_bands(close)# 平均真实波动范围
atr_14 = average_true_range(high, low, close, 14)# 威廉指标
wr_14 = williams_r(high, low, close, 14)# 随机指标
k, d = stochastic_oscillator(high, low, close, 14)# 平滑异同平均指标
sma_20 = smoothed_moving_average(close, 20)# 波动率
vol_10 = volatility(close, 10)# 商品通道指数
cci_20 = commodity_channel_index(high, low, close, 20)# 恐慌指数(这里使用对数收益率的波动率表示)
vix_index = vix(close)# 简单收益率
simple_r = simple_return(close)# 对数收益率
log_r = log_return(close)
4. 将所有指标汇总为一个 DataFrame
# 将所有计算的指标放入一个 DataFrame 中
indicators = pd.DataFrame({'MA_20': ma_20,'EMA_20': ema_20,'RSI_14': rsi_14,'MACD_Line': macd_line,'Signal_Line': signal_line,'Upper_Band': upper_band,'Lower_Band': lower_band,'ATR_14': atr_14,'WR_14': wr_14,'K': k,'D': d,'SMA_20': sma_20,'Volatility_10': vol_10,'CCI_20': cci_20,'VIX_Index': vix_index,'Simple_Return': simple_r,'Log_Return': log_r
})print(indicators.head())
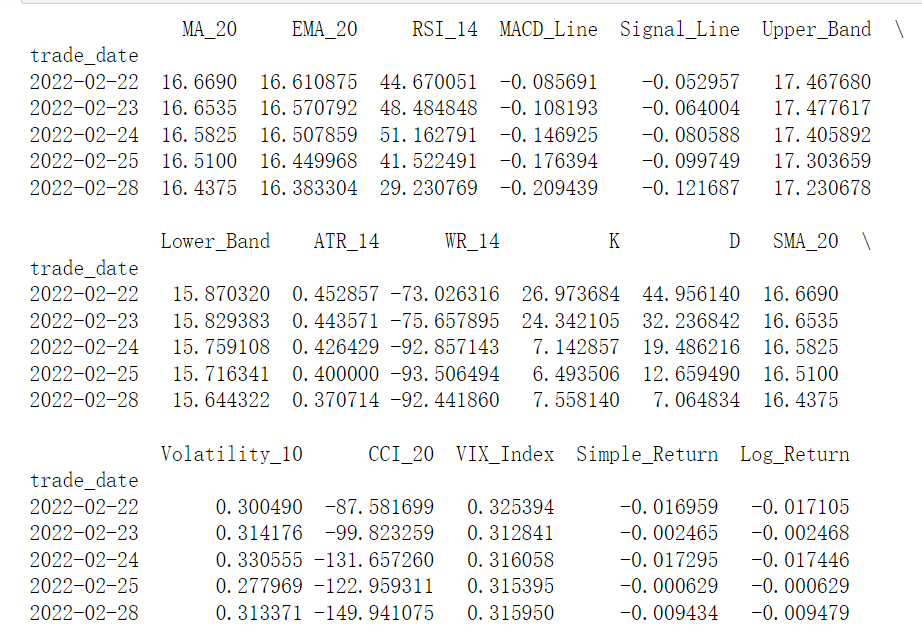
总结
通过上述代码,我们展示了如何使用 Tushare 获取股票数据,并计算多种常见的金融量化指标。这些指标可以帮助分析市场趋势、评估风险和收益,从而构建更为复杂的交易策略。在实际应用中,可以根据自己的需求调整指标的参数和选择的时间窗口,并结合其他数据源和工具进行更深入的分析。
相关文章:

002 | 常见的金融量化指标计算
金融量化指标 在金融量化分析中,常用的指标可以帮助我们判断市场走势、评估风险和收益,以及构建交易策略。以下是一些常见的金融量化指标及其计算方法的详细教程,包括公式与Python代码实现。 1. 移动平均线(Moving Average, MA&…...

Web Vitals:提升用户体验的关键指标
Web Vitals 是 Google 提出的一套核心网页性能指标,旨在帮助开发者理解和优化网站的用户体验。这些指标分为核心 Web Vitals 和附加 Web Vitals,涵盖了加载性能、交互性和视觉稳定性三个方面。以下是详细的介绍和如何使用 Web Vitals 来优化你的网站。 …...

c#中的约束、TimeSpan、defult、operator
c#中的约束 在C#中,约束(Constraints)用于限制泛型类型参数的类型,以确保泛型类型或方法在编译时能够满足特定的要求。约束允许开发者指定泛型类型参数必须满足的条件,比如实现特定的接口或继承自特定的类。以下是一些…...

挖矿木马攻破了服务器
最近被国外的挖矿木马攻破了服务器 根据非法登录,用 #last指令查看登录ip 首先删掉登录主机 #kill -9 pts/0 第二步 #top 看看什么占用cpu高 第三步杀死狂刷CPU的服务 过一分钟后,服务又开始狂刷cpu。 第四步根据pid查到服务地址 #systemctl status…...

从容应对技术面试:策略、技巧与成功案例
欢迎来到我的博客,很高兴能够在这里和您见面!欢迎订阅相关专栏: 工💗重💗hao💗:野老杂谈 ⭐️ 全网最全IT互联网公司面试宝典:收集整理全网各大IT互联网公司技术、项目、HR面试真题. ⭐️ AIGC时代的创新与未来:详细讲解AIGC的概念、核心技术、应用领域等内容。 ⭐…...

Spring Boot 整合 RestTemplate:详解与实战
Spring Boot 整合 RestTemplate:详解与实战指南 一、引言二、依赖添加Maven 示例:Gradle 示例: 三、创建 RestTemplate 实例四、使用 RestTemplate 发起请求五、处理响应六、高级用法1. 自定义 RestTemplate 实例2. 文件上传、下载以及常见的…...

【利用模板模式和责任链模式实现数据校验】
利用模板模式和责任链模式实现数据校验 一、业务背景二、模板模式和责任链模式代码实现1、数据校验抽象处理器ValidateHandler2、数据校验责任链工具类ValidateChainUtil3、网元调整数据校验抽象类AbstractNodeCheckHandler4、依次定义3个责任链handler,通过Order注…...

学习笔记第十九天
1.标准I/O的基本概念 标准输入(stdin):默认是指键盘输入。 标准输出(stdout):默认是指显示器输出。 标准错误(stderr):用于输出错误信息,也是指向显示器&…...

设计模式 - 单例模式
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝你生活愉快! 文章目录 引言一、单例模…...

fastapi之WebSockets
文章目录 WebSockets基本概念FastAPI 中的 WebSocket 支持WebSocket 应用示例示例 1: 简单的 WebSocket 连接解释 示例 2: 广播消息的 WebSocket 实现解释 客户端代码示例 完整示例项目结构服务器端代码 (main.py)解释 简单的前端客户端 (static/index.html)解释 测试 相关代码…...

Kotlin 和 Java区别
Kotlin 和 Java 是两种主要用于 Android 开发的编程语言,它们之间有一些关键的区别: 1. 语法简洁性: Kotlin:具有更简洁的语法,减少了冗余代码。例如,Kotlin 支持类型推断,避免了大量的样板…...

windows 达梦到ORACLE dblink
达梦通过DBLINK访问Oracle数据库有两种: 方式一:通过Oracle oci接口; 方式二:一种是通过ODBC数据源的方式。 本案例选择使用Oralce OCI的方式去访问Oracle数据库。 配置Oracle OCI客户端 下载地址:https://www.oracle.com/database/techno…...

大数据应用组件
1、数据存储1.1、hive->hdfs、mapredus1.2、ClickHouse1.3、Elasticsearch1.4、PostgreSQL1.5、HBase 2、数据抽取2.1、Kettle2.2、DataX2.3、Canal2.4、Flink CDC2.5、Sqoop2.6、Filebeat&Logstash(日志) 3、任务编排3.1、Apache DolphinScheduler 4、数据处理4.1、spa…...
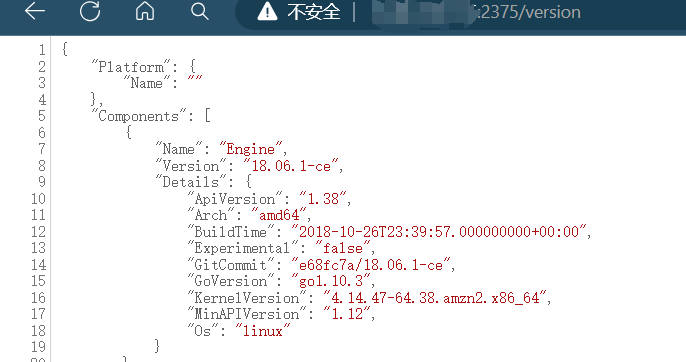
Docker Remote API未授权访问漏洞
9.Docker Remote API未授权访问漏洞 步骤一:使用以下Fofa语句对Docker产品进行搜索. port"2375" 步骤二:直接使用浏览器访问以下路径 /version#查看版本信息 /info#查看容器信息 漏洞修复 1.端口访问控制 对2375端口做网络访问控制,如设置iptables…...

算法训练.
一.扩散 题解: 计算点之间的距离,然后对图进行处理即可,这个数据规模较小,因此我使用了floyd,还有最小生成树和二份答案加并查集的写法; 代码: #include <iostream> #include <cstring> #in…...

08、MySQL-事务
目录 1、事务简介 2、事务操作 2.1 方式一 2.2 方式二 3、事务四大特性 4、并发事务问题 5、事务隔离级别 1、事务简介 事务是一组操作的集合,它是一个不可分割的工作单位,事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求,…...

2024 年的 Node.js 生态系统
数据来源于 Node.js Toolbox,网站展示了 Node.js 生态系统中积极维护且流行的库。...

LVS(Linux Virtual Server)
简介 LVS(Linux Virtual Server)是一个高性能的开源负载均衡解决方案,它通过在Linux内核中实现IPVS(IP Virtual Server)模块来提供负载均衡功能。LVS能够将外部请求根据特定的算法分发到后端的多个服务器上,…...

回顾Python
一、python基础 1、环境python2、python3 [rootpython ~]# yum list installed | grep python #检查是否有python包 [rootpython ~]# yum list installed | grep epel #检查是否有epel包 [rootpython ~]# yum -y install epel-release [rootpython ~]# yum -y install …...

【数据结构】队列,你必须知道的内部原理!!!
🌞🌞🌞生活本就沉闷,但跑起来就会有风 ~~~ 前言: 🌟🌟Hello家人们,这期讲解数据结构队列的基础知识,希望你能帮到屏幕前的你。 📚️上期博客在这里࿱…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
