JavaDS —— 位图(BitSet)与 布隆过滤器
位图
引入问题:给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。
首先要注意 40 亿个数据如果使用 整型(int) 来存放的话,就是要 40 亿个整型,一个整型有4个字节,一个字节有8个比特位,我们换算一下,40亿个字节差不多需要 15 GB 来存储,我们可以这样简便的记忆 10亿 个字节约等于 1GB
一般情况下,大家的电脑运行内存为 16GB 或者 更大的 32GB,但是我们不可能真的把这40亿 的整型数据存储进去,我们的电脑运行内存还有其他应用程序也占用着,所以我们就要想办法去缩小存储空间,这时候就可以考虑位图了
概念
位图,就是用每一位来存放某种状态,适用于海量数据,整数,数据无重复的场景。通常是用来判
断某个数据存不存在的。
位图并不是将数据存储进去,而是将这个数据的状态存储进去(即该数据存在或者不存在),位图利用比特位的 0 与 1 来表示数据的状态,通过映射关系来进行存储与读取。
举个例子:
这是位图的初始状态:

位图上面的红色 7 ~ 0 的数字大家可以自行定义顺序,可以逆序,也可以顺序,只是映射关系不同,我这里使用的是逆序
我们来插入数据,使用映射关系:使用除法式子确定下标,取模来确定具体的比特位


模拟实现
成员变量,这里我使用字节数组 byte[] 来模拟位图,源码底层是使用 long[] ,然后再加上一个统计目前元素个数的成员变量 useSize.
提供两个构造方法,注意带参数的构造方法是为了让用户自行设置大小,但是用户设计的是元素的多少,而实际我们每次开辟一个字节就可以保存 8 个元素,这里要注意换算关系。
public MyBitSet() {this.elem = new byte[1];}public MyBitSet(int size) {if(size < 0) {throw new IndexOutOfBoundsException("设置的大小无效");}int num = size / 8 + 1;this.elem = new byte[num];}
在存储数据的时候,先通过映射关系来确定下标,如果下标越界,数据就要扩容,然后再存储数据,这里该如何存储数据,我们可以让 1 左移 val % 8 个位置,这样就可以对齐到这个数据的具体的比特位,然后我们再考虑使用什么位运算符来进行计算,如果比特位本身为1说明再次存储相同的数据还是为 1 ,从这里就可以看出位图无法存储相同的数据(有去重的功能),如果比特位原本为 0 那插入数据之后就要变成 1, 可以看出 这里要使用的是 或运算(|)
public void set(int val) {int index = val / 8;if(index > elem.length) {elem = Arrays.copyOf(elem, (index + 1) * 2);}elem[index] |= 1 << (val % 8);useSize++;}
是否存在某个元素:
这里要注意的是要使用的是 & 运算符
public boolean get(int val) {int index = val / 8;if(index >= elem.length) {return false;}if((elem[index] & (1 << (val % 8))) == 0) {return false;}return true;}
删除:
删除元素的时候,要注意是只删除对应的元素,如果该元素存在对应的比特位为 1,先按位取反 (1 << (val % 8)) 然后再与运算,这样就可以删除成功了。
public boolean remove(int val) {int index = val / 8;if(index >= elem.length) {return false;}elem[index] &= (~(1 << (val % 8)));useSize--;return true;}
获取元素个数:
public int size() {return useSize;}
最终代码
public class MyBitSet {private byte[] elem;private int useSize;public MyBitSet() {this.elem = new byte[1];}public MyBitSet(int size) {if(size < 0) {throw new IndexOutOfBoundsException("设置的大小无效");}int num = size / 8 + 1;this.elem = new byte[num];}public void set(int val) {int index = val / 8;if(index >= elem.length) {elem = Arrays.copyOf(elem, (index + 1) * 2);}elem[index] |= (1 << (val % 8));useSize++;}public boolean get(int val) {int index = val / 8;if(index >= elem.length) {return false;}if((elem[index] & (1 << (val % 8))) == 0) {return false;}return true;}public boolean remove(int val) {int index = val / 8;if(index >= elem.length) {return false;}elem[index] &= (~(1 << (val % 8)));useSize--;return true;}public int size() {return useSize;}
}
BitSet
在java.util这个包下有一个 BitSet 的类,这个就是Java提供给我们的位图的数据结构:
| 方法 | 说明 |
|---|---|
| BitSet() | 无参的构造方法 |
| BitSet(int nbits) | 可以设置位图的大小 |
| void set(int bitIndex) | 插入数据 |
| boolean get(int bitIndex) | 查看数据是否存在 |
| int size() | 位图存放的元素总数 |
位图的应用
- 快速查找某个数据是否在一个集合中
- 排序 + 去重
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
排序是因为位图存放的数据已经有序,我们只需要遍历位图依次打印出数据即为有序。
布隆过滤器
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结
构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函
数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
引用场景:
一个像 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件(email)提供商,总是需要过滤来自发送垃
圾邮件的人(spamer)的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者
不停地在注册新的地址,全世界少说也有几十亿个发垃圾邮件的地址,将他们都存起来则需要大量的网络服
务器。
如果用哈希表,每存储一亿个 email 地址, 就需要 1.6GB 的内存(用哈希表实现的具体办法是将每一个
email 地址对应成一个八字节的信息指纹,然后将这些信息指纹存入哈希表,由于哈希表的存储效率一般只有
50%,因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB, 即十六亿字节的内存)。因此
存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机,一般服务器是无法存储的。
小结:
- 用哈希表存储用户记录,缺点:浪费空间
- 用位图存储用户记录,缺点:位图一般只能处理整形,如果内容编号是字符串,就无法处理了。
- 将哈希与位图结合,即布隆过滤器
插入
布隆过滤器的思想是将一个元素用多个不同的哈希函数映射到一个位图中,因此被映射到的位置的比特位一定为1
具体使用多少个哈希函数是可以通过数学进行计算的。并且哈希函数的设置也是有规定的,作为开发人员我们就使用就可以了。


查找
分别计算每个哈希值对应的比特位置存储的是否为零,只要有一个为零,代表该元素一定不在哈希表中,否则可能在哈希表中。
注意:布隆过滤器如果说某个元素不存在时,该元素一定不存在,如果该元素存在时,该元素可能存在,因
为有些哈希函数存在一定的误判。
举个例子:如果一个字符串通过不同的哈希函数映射到的位置分别为 0,3,4,刚好和 上面的 world 重合,但是这个字符串却本身不存在,只是正好哈希值和另一个元素重合,所以可能会存在误判
删除
传统的布隆过滤器不能直接支持删除工作,因为在删除一个元素时,可能会影响其他元素。
一种支持删除的方法:将布隆过滤器中的每个比特位扩展成一个小的计数器,插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一,删除元素时,给k个计数器减一,通过多占用几倍存储空间的代价来增加删除操作。
缺陷:
- 无法确认元素是否真正在布隆过滤器中【会有误判】
- 存在计数回绕【回绕意思为:溢出】
模拟实现
class SimpleHash {public int cap;//当前容量public int seed;//随机值public SimpleHash(int cap,int seed) {this.cap = cap;this.seed = seed;}//根据seed不同 创建不能的哈希函数int hash(String key) {int h;return (key == null) ? 0 : (seed * (cap-1)) & ((h = key.hashCode()) ^ (h >>> 16));}}public class BloomFilter {//默认大小public static final int DEFAULT_SIZE = 1 << 20;//位图public BitSet bitSet;//记录存了多少个数据public int usedSize;public static final int[] seeds = {5,7,11,13,27,33};public SimpleHash[] simpleHashes;public BloomFilter() {bitSet = new BitSet(DEFAULT_SIZE);simpleHashes = new SimpleHash[seeds.length];for (int i = 0; i < simpleHashes.length; i++) {simpleHashes[i] = new SimpleHash(DEFAULT_SIZE,seeds[i]);}}public void set(String val) {for (int i = 0; i < simpleHashes.length; i++) {int hash = simpleHashes[i].hash(val);bitSet.set(hash);}usedSize++;}public boolean get(String val) {for (int i = 0; i < simpleHashes.length; i++) {int hash = simpleHashes[i].hash(val);if(!bitSet.get(hash)) {return false;}}return true;}public int size() {return usedSize;}
}
布隆过滤器优点
- 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
- 哈希函数相互之间没有关系,方便硬件并行运算
- 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
- 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
- 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
- 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
布隆过滤器缺陷
- 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
- 不能获取元素本身
- 一般情况下不能从布隆过滤器中删除元素
- 如果采用计数方式删除,可能会存在计数回绕问题
布隆过滤器使用场景
- google的guava包中有对Bloom Filter的实现
- 网页爬虫对URL的去重,避免爬去相同的URL地址。
- 垃圾邮件过滤,从数十亿个垃圾邮件列表中判断某邮箱是否是垃圾邮箱。
- 解决数据库缓存击穿,黑客攻击服务器时,会构建大量不存在于缓存中的key向服务器发起请求,在数
据量足够大的时候,频繁的数据库查询会导致挂机。 - 秒杀系统,查看用户是否重复购买。
海量数据处理
哈希切割
给一个超过 100G 大小的log file,log 存在log中存着IP地址, 设计算法找到出现次数最多的IP地址? 与上题条件相同,如何找到top K的IP?
答:使用哈希切割,将这个大文件通过哈希切割分成若干个小文件,每一个小文件只存储一个IP地址,剩下的就简单了。
位图应用
1.给定100亿个整数,设计算法找到只出现一次的整数?
答:解法一:使用哈希切割,将数字哈希到对应的小文件中
解法二:使用两个位图(bitSet1 和 bitSet2),当插入数据的时候,先检查 bitSet1 的比特位是否为0,是则变为1,不是则在 bitSet2插入,这样的话,我们还可以进一步划分,当 bitSet1 为0 、bitSet2 也为0 时,则该数据重未出现过,
当 bitSet1 为0 、bitSet2 也为0 时,则该数据出现过一次,
当 bitSet1 为0 、bitSet2 也为0 时,则该数据出现过两次,
当 bitSet1 为0 、bitSet2 也为0 时,则该数据出现过三次及以上
解法三:使用一个位图,这时候我们可以利用解法二,将两个比特位表示一个数据的状态:
这样的话,就不能直接使用Java 提供的位图了,我们需要自己手动搓一个位图,映射关系也要修改。
举个例子:如果插入数据 4 ,4 / 4 = 1 (说明要插入到 数组的 1 下标)4 % 4 * 2= 0(说明要修改的是 0 号位置与 1 号位置)
所以这时候映射关系应该为 index = num / 4, i = num % 4 * 2
2.给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
答:解法一:使用哈希切割
解法二:使用一个位图:遍历第一个文件将数据保存到 bitSet1 ,遍历第二个文件,在遍历第二个文件的同时,检查数据是否也出现在 bitSet1
或者使用两个位图,分别保存两个文件的数据,然后将两个位图按位与 &
拓展:
并集:两个位图按位或 |
差集:(差集 的概念是所有属于A且不属于B的元素构成的集合),这里指属于位图1但不属于位图2 和 属于位图2但不属于位图1 的元素集合,那么将位图1 按位异或 ^ 位图2
3.位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
答:解法一:使用哈希切割
解法二:使用两个位图
解法三:使用一个位图(两个比特位表示一个整数的状态)
布隆过滤器应用
1.给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和
近似算法
精确算法:使用哈希切割或者两个位图
近似算法:使用布隆过滤器,先将第一个文件存储进布隆过滤器中,再遍历第二个文件同时查看布隆过滤器。
2.如何扩展BloomFilter使得它支持删除元素的操作
布隆过滤器中的每个比特位扩展成一个小的计数器,删除的时候计数器减1
相关文章:

JavaDS —— 位图(BitSet)与 布隆过滤器
位图 引入问题:给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。 首先要注意 40 亿个数据如果使用 整型(int) 来存放的话,就是要 40 亿个整型,一个整型有…...

如何确保场外个股期权交易的安全?
如何确保场外个股期权交易的安全?投资者可以采取以下措施,以提高交易的安全性和减少风险: 增强知识储备:深入学习期权的基础知识,包括不同类型的期权、它们的权利和义务、定价方式以及风险特性,从而提升自…...

第2章:LabVIEW FPGA未来发展方向《LabVIEW ZYNQ FPGA宝典》
2.1:NI的LabVIEW FPGA未来战略部署 在展望NI公司的LabVIEW FPGA技术未来发展趋势之前,让我们先来回顾一下LabVIEW与FPGA的技术发展历程,如图2-1所示。可以看出,NI公司的LabVIEW FPGA软件一方面是跟随Xilinx最新的FPGA硬件可持续发…...

苹果电脑维护工具:CleanMyMac X让你的Mac焕发新生!
在我们的数字生活中,苹果电脑(Mac)已成为不可或缺的一部分,无论是为工作披星戴月,还是为娱乐畅游云端。但是,就像任何长时间运行的机器一样,Mac也可能会因为积累的文件和不必要的数据而开始变慢…...

MySQL2 DML数据操纵语言和SQL约束
DML和SQL约束 SQL-DML1.添加数据2.修改数据3.删除 TRUNCATE和DELETE的区别:SQL-约束Primary Key创建主键约束单列主键联合主键**验证主键约束**删除主键约束设置主键自增AUTO_INCREMENTdelete和truncate删除后,主键的自增 SQL-唯一约束UNIQUE创建唯一约束…...

Ubuntu 20.04 中安装 Nginx (通过传包编译的方式)、开启关闭防火墙、开放端口号
文章目录 前言一、安装包下载二、上传服务器并解压缩三、依赖配置安装四、生成编译脚本五、编译六、查看是否编译完成七、开始安装八、查看是否安装成功九、设置为开机自启动 前言 参考大佬文章并在基础上做了点修改,发篇文章记录下 防止下次遇到。 参考文章&#…...

解决no main manifest attribute错误
文章目录 0. 背景1. java程序如何运行2. jar是什么3. java -jar test-1.0-SNAPSHOT.jar:4. 添加执行入口 0. 背景 在开发Spring boot项目的时候,有时候会需要使用java -jar test-1.0-SNAPSHOT.jar指令来运行开发的java应用,但是很不幸&#…...
002 | 常见的金融量化指标计算
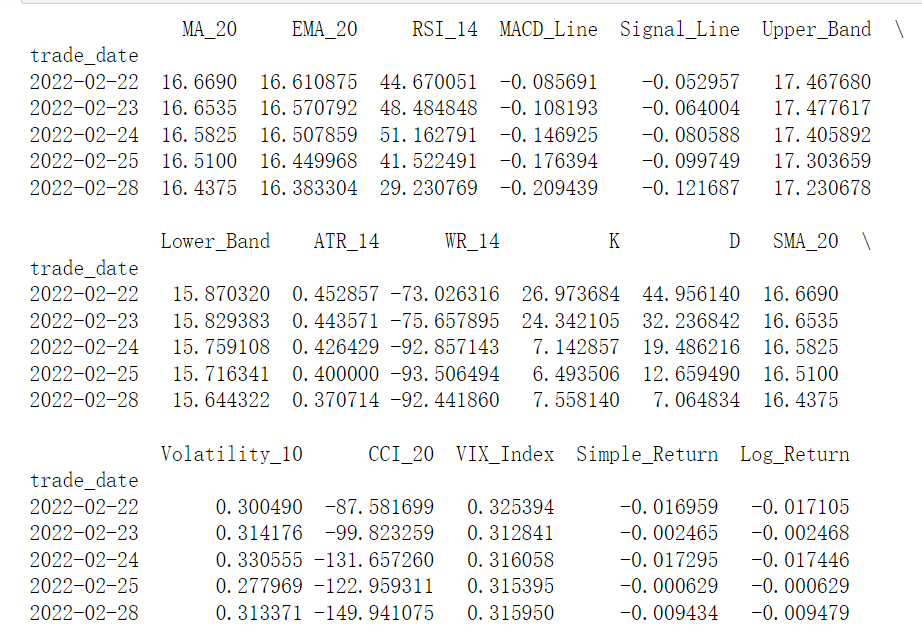
金融量化指标 在金融量化分析中,常用的指标可以帮助我们判断市场走势、评估风险和收益,以及构建交易策略。以下是一些常见的金融量化指标及其计算方法的详细教程,包括公式与Python代码实现。 1. 移动平均线(Moving Average, MA&…...

Web Vitals:提升用户体验的关键指标
Web Vitals 是 Google 提出的一套核心网页性能指标,旨在帮助开发者理解和优化网站的用户体验。这些指标分为核心 Web Vitals 和附加 Web Vitals,涵盖了加载性能、交互性和视觉稳定性三个方面。以下是详细的介绍和如何使用 Web Vitals 来优化你的网站。 …...

c#中的约束、TimeSpan、defult、operator
c#中的约束 在C#中,约束(Constraints)用于限制泛型类型参数的类型,以确保泛型类型或方法在编译时能够满足特定的要求。约束允许开发者指定泛型类型参数必须满足的条件,比如实现特定的接口或继承自特定的类。以下是一些…...

挖矿木马攻破了服务器
最近被国外的挖矿木马攻破了服务器 根据非法登录,用 #last指令查看登录ip 首先删掉登录主机 #kill -9 pts/0 第二步 #top 看看什么占用cpu高 第三步杀死狂刷CPU的服务 过一分钟后,服务又开始狂刷cpu。 第四步根据pid查到服务地址 #systemctl status…...

从容应对技术面试:策略、技巧与成功案例
欢迎来到我的博客,很高兴能够在这里和您见面!欢迎订阅相关专栏: 工💗重💗hao💗:野老杂谈 ⭐️ 全网最全IT互联网公司面试宝典:收集整理全网各大IT互联网公司技术、项目、HR面试真题. ⭐️ AIGC时代的创新与未来:详细讲解AIGC的概念、核心技术、应用领域等内容。 ⭐…...

Spring Boot 整合 RestTemplate:详解与实战
Spring Boot 整合 RestTemplate:详解与实战指南 一、引言二、依赖添加Maven 示例:Gradle 示例: 三、创建 RestTemplate 实例四、使用 RestTemplate 发起请求五、处理响应六、高级用法1. 自定义 RestTemplate 实例2. 文件上传、下载以及常见的…...

【利用模板模式和责任链模式实现数据校验】
利用模板模式和责任链模式实现数据校验 一、业务背景二、模板模式和责任链模式代码实现1、数据校验抽象处理器ValidateHandler2、数据校验责任链工具类ValidateChainUtil3、网元调整数据校验抽象类AbstractNodeCheckHandler4、依次定义3个责任链handler,通过Order注…...

学习笔记第十九天
1.标准I/O的基本概念 标准输入(stdin):默认是指键盘输入。 标准输出(stdout):默认是指显示器输出。 标准错误(stderr):用于输出错误信息,也是指向显示器&…...

设计模式 - 单例模式
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝你生活愉快! 文章目录 引言一、单例模…...

fastapi之WebSockets
文章目录 WebSockets基本概念FastAPI 中的 WebSocket 支持WebSocket 应用示例示例 1: 简单的 WebSocket 连接解释 示例 2: 广播消息的 WebSocket 实现解释 客户端代码示例 完整示例项目结构服务器端代码 (main.py)解释 简单的前端客户端 (static/index.html)解释 测试 相关代码…...

Kotlin 和 Java区别
Kotlin 和 Java 是两种主要用于 Android 开发的编程语言,它们之间有一些关键的区别: 1. 语法简洁性: Kotlin:具有更简洁的语法,减少了冗余代码。例如,Kotlin 支持类型推断,避免了大量的样板…...

windows 达梦到ORACLE dblink
达梦通过DBLINK访问Oracle数据库有两种: 方式一:通过Oracle oci接口; 方式二:一种是通过ODBC数据源的方式。 本案例选择使用Oralce OCI的方式去访问Oracle数据库。 配置Oracle OCI客户端 下载地址:https://www.oracle.com/database/techno…...

大数据应用组件
1、数据存储1.1、hive->hdfs、mapredus1.2、ClickHouse1.3、Elasticsearch1.4、PostgreSQL1.5、HBase 2、数据抽取2.1、Kettle2.2、DataX2.3、Canal2.4、Flink CDC2.5、Sqoop2.6、Filebeat&Logstash(日志) 3、任务编排3.1、Apache DolphinScheduler 4、数据处理4.1、spa…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

Angular中Webpack与ngx-build-plus 浅学
Webpack 在 Angular 中的概念 Webpack 是一个模块打包工具,用于将多个模块和资源打包成一个或多个文件。在 Angular 项目中,Webpack 负责将 TypeScript、HTML、CSS 等文件打包成浏览器可以理解的 JavaScript 文件。Angular CLI 默认使用 Webpack 进行项目…...
