一篇文章带你解析完整数据结构-----满满干活值得收藏
数据结构是计算机科学中的一个重要分支,它涉及到计算机存储、组织数据的方式。以下是数据结构的主要知识点:
基本概念
- 数据(Data)。
- 数据元素(Data Element):
- 数据项(Data Item):
- 数据对象(Data Object):
- 数据结构(Data Structure):
逻辑结构(Logical Structure)
物理结构(Physical Structure)或存储结构
抽象数据类型(Abstract Data Type, ADT)
抽象数据类型(Abstract Data Type, ADT)
当然,让我们更详细地探讨数据结构的基本概念:
数据结构的分类
- 逻辑结构:
- 集合结构
- 线性结构
- 树形结构
- 图形结构
- 物理结构(存储结构):
- 顺序存储结构
- 链式存储结构
- 索引存储结构
- 散列存储结构
常见数据结构
- 线性表
- 数组
- 链表
- 单链表
- 双链表
- 循环链表
- 栈
- 队列
- 循环队列
- 链队列
- 树形结构
- 二叉树
- 满二叉树
- 完全二叉树
- 平衡二叉树(AVL树)
- 二叉查找树(BST)
- 多路树
- B树
- B+树
- 红黑树
- 堆
- 最大堆
- 最小堆
- 哈夫曼树
- 二叉树
- 图形结构
- 邻接矩阵
- 邻接表
- 十字链表
- 邻接多重表
- 集合
- 并查集
算法
- 排序算法
- 冒泡排序
- 选择排序
- 插入排序
- 快速排序
- 归并排序
- 堆排序
- 希尔排序
- 查找算法
- 顺序查找
- 二分查找
- 哈希查找
算法评价
- 时间复杂度
- 空间复杂度
其他
- 递归
- 动态规划
- 贪心算法
- 回溯法
以上是数据结构的基本知识点,每个知识点下都包含了大量的详细内容,需要深入学习和实践才能掌握。
高级数据结构
- 跳表(Skip List)
- 伸展树(Splay Tree)
- Treap(树堆)
- Trie(前缀树)
- 后缀树
- B树及其变体(B树、B+树、B*树)
- 斐波那契堆
- 配对堆(Pairing Heap)
- 布隆过滤器(Bloom Filter)
- 计数位数组(Counting Bloom Filter)
- Cuckoo哈希
- LSM树(Log-Structured Merge-Tree)
- 跳跃表(Skip List)
特殊数据结构
- 并查集(Union-Find)
- 线段树(Segment Tree)
- 树状数组(Binary Indexed Tree / Fenwick Tree)
- 平衡树(如2-3树、红黑树)
- 区间树(Interval Tree)
- 优先队列(基于堆实现)
数据结构在特定领域的应用
- 图算法在网络分析中的应用
- 数据结构在数据库索引中的应用
- 数据结构在算法竞赛中的应用
数据结构与算法的结合
- 动态规划中的状态存储结构
- 贪心算法中的数据选择结构
- 回溯算法中的状态表示结构
现代数据结构趋势
- 分布式数据结构
- 并行数据结构
- 数据结构在内存数据库中的应用
数据结构的实现和优化
- 缓存优化
- 内存管理
- 数据压缩技术

数据(Data)
- 定义:数据是信息的表示形式,可以是数字、文本、图像、声音等。
- 特性:
- 可处理性:数据必须能被计算机程序处理。
- 可表示性:数据需要以某种形式存在,如二进制、字符等。
数据元素(Data Element)
- 定义:数据元素是数据的基本单元,它可以是单个值或一组值的集合。
- 例子:在数据库中,一条记录可以是一个数据元素,它包含了多个数据项,如姓名、地址、电话号码等。
数据项(Data Item)
- 定义:数据项是数据元素中的最小单位,不能再被分割。
- 例子:在一个学生的信息记录中,学号、姓名、性别等每个单独的信息都是数据项。
数据对象(Data Object)
- 定义:数据对象是具有相同性质的数据元素的集合,它可以是整个数据集或数据集的一部分。
- 例子:所有员工的工资记录可以构成一个数据对象。

数据结构(Data Structure)
- 定义:数据结构是数据对象中数据元素之间关系的描述,它定义了数据的组织、管理和存储方式。
- 重要性:良好的数据结构可以提高数据处理的效率,减少存储空间的需求。
逻辑结构(Logical Structure)
- 定义:逻辑结构是指数据元素之间的逻辑关系,它不依赖于数据在计算机中的存储方式。
- 分类:
- 集合结构:数据元素之间没有特定的关系,它们只是简单地属于同一个集合。
- 线性结构:数据元素之间存在一对一的关系,如数组、链表、栈和队列。
- 树形结构:数据元素之间存在一对多的层次关系,如树和二叉树。
- 图形结构:数据元素之间存在多对多的关系,如网状结构和图。
物理结构(Physical Structure)或存储结构
- 定义:物理结构是指数据在计算机存储器中的实际表示方式。
- 分类:
- 顺序存储结构:
- 数据元素在内存中连续存放,通过索引直接访问。
- 优点:访问速度快。
- 缺点:插入和删除操作可能需要移动大量元素。
- 链式存储结构:
- 数据元素可以分散存储,通过指针连接。
- 优点:插入和删除操作不需要移动其他元素。
- 缺点:访问速度相对较慢,因为需要通过指针遍历。
- 索引存储结构:
- 通过建立索引表来快速访问数据元素。
- 优点:可以快速定位数据元素。
- 缺点:索引表本身需要额外的存储空间。
- 散列存储结构:
- 通过散列函数直接计算出数据元素的存储地址。
- 优点:通常可以实现快速的插入和查找操作。
- 缺点:散列函数的设计和冲突解决策略较为复杂。

- 顺序存储结构:
抽象数据类型(Abstract Data Type, ADT)
- 定义:抽象数据类型是一组数据和施加于其上的一组操作的总称,它定义了数据的逻辑特性及其操作接口,而不涉及具体的实现细节。
- 例子:栈、队列、列表等都是抽象数据类型的例子。
- 特性:
- 数据抽象:只关注数据的逻辑特性,而不关心数据在计算机中的具体表示。
- 封装性:数据和操作被封装在一起,对外提供统一的接口。
理解这些概念是深入学习和应用数据结构的基础。在实际编程中,选择合适的数据结构对于编写高效、可维护的代码至关重要。
抽象数据类型(Abstract Data Type, ADT)
- 定义:一个数学模型以及定义在此模型上的一组操作。
- 举例:栈、队列、线性表、树等。
数据结构的分类主要基于数据元素之间的关系,可以分为两大类:逻辑结构和物理结构。以下是对这两大类数据结构分类的详细解释:
逻辑结构
逻辑结构是数据对象中数据元素之间的逻辑关系,与数据的存储无关,是抽象的。逻辑结构主要分为以下几种:
集合结构
- 定义:集合结构中的数据元素之间除了“属于同一个集合”的关系外,没有其他关系。
- 特点:数据元素之间没有顺序或层次关系,可以看作是一个无序的集合。

线性结构
- 定义:线性结构中的数据元素之间存在一对一的关系。
- 特点:
-
数据元素有先后顺序,除了第一个和最后一个元素外,每个元素有且只有一个前驱和后继。
-
常见的线性结构包括数组、链表、栈和队列。
-
数组:一种连续的存储结构,元素在内存中连续存放,通过索引直接访问。
-
链表:一种非连续的存储结构,元素通过指针连接,可以是单向链表、双向链表或循环链表。
-
栈:一种后进先出(LIFO)的数据结构,只允许在一端进行插入和删除操作。
-
队列:一种先进先出(FIFO)的数据结构,允许在一端插入元素,在另一端删除元素。
-
树形结构
- 定义:树形结构中的数据元素之间存在一对多的层次关系。
- 特点:
-
每个元素可以有多个后继,但只能有一个前驱(根节点除外)。
-
常见的树形结构包括二叉树、多叉树、堆、平衡树等。
-
二叉树:每个节点最多有两个子节点的树结构,包括满二叉树、完全二叉树、平衡二叉树(AVL树)、二叉查找树(BST)等。
-
多叉树:每个节点可以有多个子节点的树结构,如B树、B+树、红黑树等。
-
堆:一种特殊的树形结构,通常用于实现优先队列,分为最大堆和最小堆。
-
图形结构
- 定义:图形结构中的数据元素之间存在多对多的关系。
- 特点:
- 数据元素之间没有固定的顺序,可以是任意复杂的网络结构。
- 常见的图形结构包括无向图、有向图、加权图、网络等。
物理结构(存储结构)
物理结构是指数据在计算机中的实际存储方式,它依赖于逻辑结构。物理结构主要分为以下几种:

顺序存储结构
- 定义:顺序存储结构中,数据元素在内存中连续存放,通常利用数组实现。
- 特点:
- 访问速度快,通过索引直接访问。
- 插入和删除操作可能需要移动大量元素,效率较低。
链式存储结构
- 定义:链式存储结构中,数据元素可以分散存储,通过指针连接。
- 特点:
- 插入和删除操作不需要移动其他元素,效率较高。
- 访问速度相对较慢,因为需要通过指针遍历。
索引存储结构
- 定义:索引存储结构通过建立索引表来快速访问数据元素。
- 特点:
- 可以快速定位数据元素。
- 索引表本身需要额外的存储空间。
散列存储结构
- 定义:散列存储结构通过散列函数直接计算出数据元素的存储地址。
- 特点:
- 通常可以实现快速的插入和查找操作。
- 散列函数的设计和冲突解决策略较为复杂。
每种逻辑结构都可以采用不同的物理结构来实现,不同的实现方式会有不同的性能特点。在设计数据结构时,需要根据具体的应用场景和需求来选择合适的逻辑结构和物理结构。
当然,以下是一些常见数据结构的简单代码示例。这些示例将使用Python语言,因为它简单且易于理解。
数组(顺序存储结构)
# Python中的列表可以看作是动态数组
array = [1, 2, 3, 4, 5]
# 访问元素
print(array[2]) # 输出 3
# 修改元素
array[2] = 10
print(array) # 输出 [1, 2, 10, 4, 5]
# 添加元素
array.append(6)
print(array) # 输出 [1, 2, 10, 4, 5, 6]
# 删除元素
del array[2]
print(array) # 输出 [1, 2, 4, 5, 6]
链表(链式存储结构)
# 定义链表节点
class ListNode:def __init__(self, value=0, next=None):self.value = valueself.next = next
# 创建链表
head = ListNode(1)
head.next = ListNode(2)
head.next.next = ListNode(3)
# 遍历链表
current = head
while current:print(current.value)current = current.next
栈(线性结构,后进先出)
# 使用列表实现栈
stack = []
# 入栈
stack.append(1)
stack.append(2)
stack.append(3)
# 出栈
print(stack.pop()) # 输出 3
print(stack) # 输出 [1, 2]
队列(线性结构,先进先出)
# 使用collections.deque实现队列
from collections import deque
queue = deque()
# 入队
queue.append(1)
queue.append(2)
queue.append(3)
# 出队
print(queue.popleft()) # 输出 1
print(queue) # 输出 deque([2, 3])
二叉树(树形结构)
# 定义二叉树节点
class TreeNode:def __init__(self, value=0, left=None, right=None):self.value = valueself.left = leftself.right = right
# 创建二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
# 前序遍历
def preorderTraversal(node):if node:print(node.value)preorderTraversal(node.left)preorderTraversal(node.right)
preorderTraversal(root) # 输出 1 2 3
这些示例展示了如何使用Python实现和操作基本的数据结构。在实际应用中,这些数据结构可能会更加复杂,并且需要更多的功能和方法。
常见的数据结构主要分为以下几类,每一类都有其特定的用途和操作:

线性结构
- 数组(Array):
- 特点:固定大小的顺序存储结构,元素在内存中连续存放。
- 操作:随机访问、插入(可能需要移动元素)、删除(可能需要移动元素)。
- 链表(Linked List):
- 特点:动态大小的链式存储结构,元素通过指针连接。
- 操作:插入(不需要移动元素)、删除(不需要移动元素,但需要找到前驱节点)、遍历。
- 单向链表:每个节点只有一个指向下一个节点的指针。
- 双向链表:每个节点有两个指针,分别指向前一个和后一个节点。
- 循环链表:链表的最后一个节点指向第一个节点,形成一个环。
- 栈(Stack):
- 特点:后进先出(LIFO)的数据结构。
- 操作:压栈(push)、出栈(pop)、查看栈顶元素。
- 队列(Queue):
- 特点:先进先出(FIFO)的数据结构。
- 操作:入队(enqueue)、出队(dequeue)、查看队首元素。
树形结构
- 二叉树(Binary Tree):
- 特点:每个节点最多有两个子节点。
- 操作:遍历(前序、中序、后序)、查找、插入、删除。
- 二叉查找树(BST):左子树的所有节点都比当前节点小,右子树的所有节点都比当前节点大。
- 平衡二叉树(AVL):任何节点的两个子树的高度差不超过1。
- 堆(Heap):
- 特点:特殊的完全二叉树,通常用于实现优先队列。
- 操作:插入、删除最大/最小元素。
- B树(B-Tree):
- 特点:多路平衡查找树,用于磁盘存储。
- 操作:插入、删除、查找。
图形结构
- 图(Graph):
- 特点:由节点(顶点)和边组成的数据结构,用于表示对象间多对多的关系。
- 操作:遍历(深度优先搜索DFS、广度优先搜索BFS)、路径查找。
- 无向图:边没有方向。
- 有向图:边有方向。
- 加权图:边有权重。
其他结构
- 哈希表(Hash Table):
- 特点:通过哈希函数将键映射到表中一个位置来访问记录,用于快速查找。
- 操作:插入、删除、查找。
- 集合(Set):
- 特点:存储不重复元素的集合。
- 操作:添加、删除、查找。
- 字典(Dictionary):
- 特点:键值对集合,通常通过哈希表实现。
- 操作:插入、删除、查找。
这些数据结构在不同的编程语言中有不同的实现方式,它们的应用范围广泛,从简单的数据存储到复杂的数据处理都有它们的身影。
当然,以下是一些常见数据结构的简单代码示例。这些示例将使用Python语言,因为它简单且易于理解。
数组(顺序存储结构)
# Python中的列表可以看作是动态数组
array = [1, 2, 3, 4, 5]
# 访问元素
print(array[2]) # 输出 3
# 修改元素
array[2] = 10
print(array) # 输出 [1, 2, 10, 4, 5]
# 添加元素
array.append(6)
print(array) # 输出 [1, 2, 10, 4, 5, 6]
# 删除元素
del array[2]
print(array) # 输出 [1, 2, 4, 5, 6]
链表(链式存储结构)
# 定义链表节点
class ListNode:def __init__(self, value=0, next=None):self.value = valueself.next = next
# 创建链表
head = ListNode(1)
head.next = ListNode(2)
head.next.next = ListNode(3)
# 遍历链表
current = head
while current:print(current.value)current = current.next
栈(线性结构,后进先出)
# 使用列表实现栈
stack = []
# 入栈
stack.append(1)
stack.append(2)
stack.append(3)
# 出栈
print(stack.pop()) # 输出 3
print(stack) # 输出 [1, 2]
队列(线性结构,先进先出)
# 使用collections.deque实现队列
from collections import deque
queue = deque()
# 入队
queue.append(1)
queue.append(2)
queue.append(3)
# 出队
print(queue.popleft()) # 输出 1
print(queue) # 输出 deque([2, 3])
二叉树(树形结构)
# 定义二叉树节点
class TreeNode:def __init__(self, value=0, left=None, right=None):self.value = valueself.left = leftself.right = right
# 创建二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
# 前序遍历
def preorderTraversal(node):if node:print(node.value)preorderTraversal(node.left)preorderTraversal(node.right)
preorderTraversal(root) # 输出 1 2 3
这些示例展示了如何使用Python实现和操作基本的数据结构。在实际应用中,这些数据结构可能会更加复杂,并且需要更多的功能和方法。
当然,这里有一些更复杂的数据结构的代码示例。

哈希表(Hash Table)
class HashTable:def __init__(self):self.size = 10self.table = [None] * self.sizedef _hash(self, key):return key % self.sizedef put(self, key, value):index = self._hash(key)if self.table[index] is None:self.table[index] = []self.table[index].append((key, value))def get(self, key):index = self._hash(key)if self.table[index]:for pair in self.table[index]:if pair[0] == key:return pair[1]return None
# 示例
hash_table = HashTable()
hash_table.put("apple", 1)
hash_table.put("banana", 2)
print(hash_table.get("apple")) # 输出 1
集合(Set)
# Python中的集合就是一种数据结构
fruits = {"apple", "banana", "cherry"}
# 添加元素
fruits.add("mango")
# 删除元素
fruits.remove("banana")
# 查找元素
if "apple" in fruits:print("Yes, we have apple.")
字典(Dictionary)
# Python中的字典就是一种数据结构
my_dict = {"name": "John", "age": 30, "city": "New York"}
# 访问元素
print(my_dict["name"]) # 输出 John
# 添加或修改元素
my_dict["name"] = "Doe"
# 删除元素
del my_dict["age"]
优先队列(Priority Queue)
from heapq import heappush, heappop
# 定义一个优先队列
priority_queue = []
# 插入元素(元素可以是元组,其中第一个元素是优先级,第二个元素是要存储的数据)
heappush(priority_queue, (2, "task 1"))
heappush(priority_queue, (3, "task 2"))
heappush(priority_queue, (1, "task 3"))
# 取出优先级最高的元素
print(heappop(priority_queue)) # 输出 (1, "task 3")
这些示例展示了如何使用Python实现和操作更复杂的数据结构。在实际应用中,这些数据结构可能会更加复杂,并且需要更多的功能和方法。
树形结构是一类重要的数据结构,它们在计算机科学中广泛用于存储和检索数据。以下是树形结构的详细介绍:
树形结构
二叉树
- 定义:二叉树是一种特殊的树形结构,每个节点最多有两个子节点。
满二叉树
- 定义:满二叉树是一种特殊的二叉树,除了叶子节点外,每个节点都有两个子节点。
完全二叉树
- 定义:完全二叉树是一种特殊的二叉树,除了最底层外,所有层都被完全填满,且最底层的节点都靠左排列。
平衡二叉树(AVL树)
- 定义:平衡二叉树是一种特殊的二叉树,它满足任何节点的两个子树的高度差不超过1。

二叉查找树(BST)
- 定义:二叉查找树是一种特殊的二叉树,左子树上所有节点的值都小于当前节点的值,右子树上所有节点的值都大于当前节点的值。
多路树
- 定义:多路树是一种特殊的树形结构,每个节点可以有多个子节点。
B树
- 定义:B树是一种特殊的树形结构,用于数据库索引和文件系统。它是一种多路搜索树,每个节点可以有多个子节点。
B+树
- 定义:B+树是一种特殊的树形结构,它是B树的变种,所有叶子节点包含所有的键值,且所有的叶子节点通过指针连接。
红黑树
- 定义:红黑树是一种特殊的树形结构,它满足以下性质:每个节点要么是红色,要么是黑色;根节点是黑色;每个叶子节点(NIL节点)是黑色;如果一个节点是红色,则它的两个子节点都是黑色;对每个节点,从该节点到其所有后代叶子节点的简单路径上,均包含相同数目的黑色节点。
堆
- 定义:堆是一种特殊的树形结构,通常用于实现优先队列。
最大堆
- 定义:最大堆是一种特殊的堆,每个节点的值都大于或等于其子节点的值。
最小堆
- 定义:最小堆是一种特殊的堆,每个节点的值都小于或等于其子节点的值。
哈夫曼树
- 定义:哈夫曼树是一种特殊的树形结构,它是一种带权路径长度最短的二叉树,常用于数据压缩。
图形结构
邻接矩阵
- 定义:邻接矩阵是一种特殊的图形结构,它使用二维数组来表示图中顶点之间的关系。
邻接表
- 定义:邻接表是一种特殊的图形结构,它使用链表来表示图中顶点之间的关系。
十字链表
- 定义:十字链表是一种特殊的图形结构,它使用双向链表来表示图中顶点之间的关系,并且在每个顶点的链表中包含指向其父节点的指针。
邻接多重表
- 定义:邻接多重表是一种特殊的图形结构,它使用多重链表来表示图中顶点之间的关系。
集合
并查集
- 定义:并查集是一种特殊的集合结构,它用于处理一些不交集的合并及查询问题。
以上是树形结构的基本概念和分类。在实际应用中,树形结构可以根据具体需求进行扩展和变种。
排序算法是计算机科学中的一种基本算法,用于将一组数据按照特定的顺序进行排列。排序算法可以分为内部排序和外部排序,内部排序是在内存中进行的排序,而外部排序是在硬盘等外部存储设备上进行的排序。常见的内部排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序和希尔排序等。下面将详细介绍这些排序算法的原理和实现。

冒泡排序
原理
冒泡排序的基本思想是通过相邻元素的比较和交换,将最大(或最小)的元素逐渐“冒泡”到数组的末尾。
实现
def bubble_sort(arr):n = len(arr)for i in range(n):for j in range(0, n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]
选择排序
原理
选择排序的基本思想是每次从未排序的部分中选择最小(或最大)的元素,放到已排序部分的末尾。
实现
def selection_sort(arr):n = len(arr)for i in range(n):min_index = ifor j in range(i+1, n):if arr[j] < arr[min_index]:min_index = jarr[i], arr[min_index] = arr[min_index], arr[i]
插入排序
原理
插入排序的基本思想是将一个记录插入到已排序好的有序表中,从而得到一个新的、记录数增1的有序表。
实现
def insertion_sort(arr):n = len(arr)for i in range(1, n):key = arr[i]j = i-1while j >= 0 and key < arr[j]:arr[j+1] = arr[j]j -= 1arr[j+1] = key
快速排序
原理
快速排序的基本思想是通过一趟排序将待排序记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,然后再分别对这两部分记录继续进行排序,以达到整个序列有序。
实现
def quick_sort(arr):if len(arr) <= 1:return arrpivot = arr[len(arr) // 2]left = [x for x in arr if x < pivot]middle = [x for x in arr if x == pivot]right = [x for x in arr if x > pivot]return quick_sort(left) + middle + quick_sort(right)
归并排序

原理
归并排序的基本思想是将待排序的记录序列分为若干个子序列,分别对每个子序列进行排序,再将已排序好的子序列合并,得到一个有序的记录序列。
实现
def merge_sort(arr):if len(arr) <= 1:return arrmid = len(arr) // 2left = merge_sort(arr[:mid])right = merge_sort(arr[mid:])return merge(left, right)
def merge(left, right):result = []i = j = 0while i < len(left) and j < len(right):if left[i] < right[j]:result.append(left[i])i += 1else:result.append(right[j])j += 1result.extend(left[i:])result.extend(right[j:])return result
堆排序
原理
堆排序的基本思想是将待排序的序列构造成一个大顶堆(或小顶堆),此时,整个序列的最大(或最小)值就是堆顶的根节点。将堆顶的根节点与堆数组的末尾元素进行交换,此时末尾元素就是最大(或最小)值。然后将剩余的序列重新构造成一个堆,重复以上操作
def heapify(arr, n, i):largest = i # Initialize largest as rootl = 2 * i + 1 # left = 2*i + 1r = 2 * i + 2 # right = 2*i + 2# Check if left child of root exists and is# greater than rootif l < n and arr[l] > arr[largest]:largest = l# Check if right child of root exists and is# greater than the largest so farif r < n and arr[r] > arr[largest]:largest = r# Change root, if neededif largest != i:arr[i], arr[largest] = arr[largest], arr[i] # swap# Heapify the root.heapify(arr, n, largest)def heap_sort(arr):n = len(arr)# Build a max heapfor i in range(n // 2 - 1, -1, -1):heapify(arr, n, i)# One by one extract elementsfor i in range(n-1, 0, -1):arr[i], arr[0] = arr[0], arr[i] # swapheapify(arr, i, 0)# Example usage:
arr = [12, 11, 13, 5, 6, 7]
heap_sort(arr)
print("Sorted array is", arr))
直到整个序列有序实现
def heapify(arr, n, i):largest = i # Initialize largest as rootl = 2 * i + 1 # left = 2*i + 1r = 2 * i + 2 # right = 2*i + 2# See if left child of root exists and is# greater than rootif l < n and arr[l] > arr[largest]:largest = l# See if right child of root exists and is# greater than the largest so farif r < n and arr[r] > arr[largest]:largest = r# Change root, if neededif largest != i:arr[i], arr[largest] = arr[largest], arr[i] # swap# Heapify the root.heapify(arr, n, largest)
def heap_sort(arr):n = len(arr)# Build a max heapfor i in range(n // 2 - 1, -1, -1):heapify(arr, n, i)# One by one extract elementsfor i in range(n-1, 0, -1):arr[i], arr[0] = arr[0], arr[i] # swapheapify(arr, i, 0)
希尔排序

原理
希尔排序(也称为“递减增量排序”)的基本思想是将整个无序序列分割成若干个子序列,分别进行直接插入排序。待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
实现
def shell_sort(arr):n = len(arr)gap = n // 2# 希尔排序while gap > 0:for i in range(gap, n):temp = arr[i]j = iwhile j >= gap and arr[j - gap] > temp:arr[j] = arr[j - gap]j -= gaparr[j] = tempgap //= 2
这些排序算法各有优缺点,选择哪种排序算法取决于具体的需求和应用场景。例如,快速排序和堆排序的平均和最坏时间复杂度较低,但快速排序在最坏情况下的时间复杂度为O(n^2),而堆排序和归并排序的时间复杂度始终为O(n log n)。插入排序和选择排序的时间复杂度为O(n^2),但它们在小型数据集上的性能可能优于其他排序算法。希尔排序的时间复杂度介于O(n log n)和O(n^2)之间,但它对于已经部分排序的数据集效果较好。
查找算法是计算机科学中用于在数据集中查找特定元素的方法。以下是一些常见的查找算法:
顺序查找

原理
顺序查找是最简单的查找方法,它从数据集的开始处逐个比较每个元素,直到找到目标元素或查找完毕。
实现
def sequential_search(arr, x):for i in range(len(arr)):if arr[i] == x:return i # 返回找到元素的索引return -1 # 如果没有找到元素,返回-1
二分查找
原理
二分查找是一种在有序数组中查找特定元素的搜索算法。它通过将搜索区间分成两半,然后确定目标值是在较小的子区间还是较大的子区间,以此类推,直到找到目标值或搜索区间为空。
实现
def binary_search(arr, x):low = 0high = len(arr) - 1mid = 0while low <= high:mid = (low + high) // 2# 检查中间元素if arr[mid] < x:low = mid + 1elif arr[mid] > x:high = mid - 1else:return mid # 目标值在中间return -1 # 目标值不在数组中
哈希查找

原理
哈希查找使用哈希表(哈希表是一种通过哈希函数将键映射到表中一个位置的数据结构)来存储数据,从而实现快速的查找。
实现
class HashTable:def __init__(self, size=100):self.size = sizeself.table = [None] * self.sizedef _hash(self, key):return key % self.sizedef put(self, key, value):index = self._hash(key)if self.table[index] is None:self.table[index] = []self.table[index].append((key, value))def get(self, key):index = self._hash(key)if self.table[index]:for pair in self.table[index]:if pair[0] == key:return pair[1]return None
# Example usage:
hash_table = HashTable()
hash_table.put("apple", 1)
hash_table.put("banana", 2)
print(hash_table.get("apple")) # 输出 1
这些查找算法各有优缺点,选择哪种查找算法取决于具体的需求和应用场景。例如,顺序查找适用于无序数组,而二分查找适用于有序数组。哈希查找适用于大规模数据集,但需要额外的空间来存储哈希表。
算法评价是评估算法性能的重要手段,主要包括时间复杂度和空间复杂度两个方面。

时间复杂度
时间复杂度是衡量算法运行时间的一个指标,它描述了算法执行过程中基本操作的执行次数与输入规模之间的关系。通常使用大O符号(O)来表示时间复杂度。
- 最好情况:算法执行过程中基本操作执行次数最少的情况。
- 最坏情况:算法执行过程中基本操作执行次数最多的情况。
- 平均情况:算法执行过程中基本操作执行次数的平均情况。
空间复杂度
空间复杂度是衡量算法执行过程中所需内存空间的一个指标,它描述了算法执行过程中所需内存空间与输入规模之间的关系。通常使用大O符号(O)来表示空间复杂度。
- 最好情况:算法执行过程中所需内存空间最少的情况。
- 最坏情况:算法执行过程中所需内存空间最多的情况。
- 平均情况:算法执行过程中所需内存空间的平均情况。
举例
冒泡排序
- 时间复杂度:最好情况O(n),最坏情况O(n2),平均情况O(n2)
- 空间复杂度:O(1)
快速排序
- 时间复杂度:最好情况O(n log n),最坏情况O(n^2),平均情况O(n log n)
- 空间复杂度:O(log n)(递归栈空间)
哈希查找
- 时间复杂度:平均情况O(1),最坏情况O(n)(哈希表中没有足够的空位,导致大量冲突)
- 空间复杂度:O(n)(需要一个大小为n的哈希表)
通过分析算法的时间复杂度和空间复杂度,可以对算法的性能有一个大致的了解,并选择最合适的算法来解决问题。

当然,以下是一些常见查找算法的简单代码示例。这些示例将使用Python语言,因为它简单且易于理解。
顺序查找
def sequential_search(arr, x):for i in range(len(arr)):if arr[i] == x:return i # 返回找到元素的索引return -1 # 如果没有找到元素,返回-1
# 示例
arr = [12, 11, 13, 5, 6, 7]
index = sequential_search(arr, 13)
print(f"元素13在索引{index}处找到。")
二分查找
def binary_search(arr, x):low = 0high = len(arr) - 1mid = 0while low <= high:mid = (low + high) // 2# 检查中间元素if arr[mid] < x:low = mid + 1elif arr[mid] > x:high = mid - 1else:return mid # 目标值在中间return -1 # 目标值不在数组中
# 示例
arr = [12, 11, 13, 5, 6, 7]
index = binary_search(arr, 13)
print(f"元素13在索引{index}处找到。")

哈希查找
class HashTable:def __init__(self, size=100):self.size = sizeself.table = [None] * self.sizedef _hash(self, key):return key % self.sizedef put(self, key, value):index = self._hash(key)if self.table[index] is None:self.table[index] = []self.table[index].append((key, value))def get(self, key):index = self._hash(key)if self.table[index]:for pair in self.table[index]:if pair[0] == key:return pair[1]return None
# 示例
hash_table = HashTable()
hash_table.put("apple", 1)
hash_table.put("banana", 2)
print(hash_table.get("apple")) # 输出 1
这些示例展示了如何使用Python实现和操作基本的查找算法。在实际应用中,这些算法可能会更加复杂,并且需要更多的功能和方法。
这些算法是计算机科学中的高级算法,它们在解决特定类型的问题时非常有用。下面是对这些算法的简要介绍:
递归(Recursion)
递归是一种算法设计技术,其中一个函数调用自身来解决问题。递归通常用于解决那些可以分解为较小版本的问题。
示例:计算阶乘
def factorial(n):if n == 0:return 1else:return n * factorial(n-1)
动态规划(Dynamic Programming)
动态规划是一种将复杂问题分解为更小的、相似的子问题,并存储这些子问题的解,以避免重复计算的方法。
示例:斐波那契数列
def fibonacci(n):if n <= 1:return na, b = 0, 1for i in range(2, n + 1):a, b = b, a + breturn b
贪心算法(Greedy Algorithm)
贪心算法是一种在每一步选择中都采取当前状态下最优(即看起来最有利)的选择,从而希望导致全局最优解的算法。
示例:零钱兑换
def coinChange(coins, amount):dp = [float('inf')] * (amount + 1)dp[0] = 0for coin in coins:for j in range(coin, amount + 1):dp[j] = min(dp[j], dp[j - coin] + 1)return dp[amount] if dp[amount] != float('inf') else -1
回溯法(Backtracking)
回溯法是一种通过尝试所有可能的解决方案,并在发现无效的解决方案时回退到上一步的方法。
示例:八皇后问题
def solveNQueens(n):board = [[0] * n for _ in range(n)]def isSafe(row, col, queen):for i in range(n):if board[row][i] == queen or board[i][col] == queen or (i - row == col - queen) or (i - row == queen - col):return Falsereturn Truedef solve(col):if col >= n:solutions.append(list(board))returnfor i in range(n):if isSafe(row, col, 'Q'):board[row][col] = 'Q'solve(col + 1)board[row][col] = 0solutions = []solve(0)return solutions
这些算法在实际编程中非常有用,可以帮助解决各种复杂问题。在实际应用中,这些算法可能会更加复杂,并且需要更多的功能和方法。
当然,下面我将更详细地介绍这些高级数据结构,并提供相应的代码示例。

跳表(Skip List)
跳表是一种可以实现快速查找、插入和删除操作的数据结构。它通过在原始链表中插入多个辅助链表来提高查找效率。
示例
class SkipListNode:def __init__(self, key, val):self.key = keyself.val = valself.forward = []self.backward = None
class SkipList:def __init__(self, p=0.5):self.p = pself.head = SkipListNode(None, None)self.level = 0def _random_level(self):level = 1while random.random() < self.p and level < self.level_max:level += 1return leveldef _get_node(self, key):node = self.headfor i in range(self.level, -1, -1):while node.forward[i] and node.forward[i].key < key:node = node.forward[i]return nodedef _insert_node(self, node, key, val):if node.key is None:self.level += 1node.forward = [None] * self.levelelse:node.forward.append(None)new_node = SkipListNode(key, val)new_node.backward = nodefor i in range(self.level, -1, -1):while node.forward[i] and node.forward[i].key < key:node = node.forward[i]if node.forward[i] is None:new_node.forward[i] = nodeelse:new_node.forward[i] = node.forward[i]node.forward[i].backward = new_nodenode.forward[i] = new_nodedef insert(self, key, val):if not self.head.forward[0]:self.head.forward[0] = SkipListNode(None, None)self.level = max(self.level, self._random_level())self._insert_node(self.head, key, val)def delete(self, key):node = self._get_node(key)if node.key is None:return Falsefor i in range(self.level, -1, -1):if node.forward[i]:if node.forward[i].key == key:node.forward[i].backward = node.backwardif node.backward:node.backward.forward[i] = node.forward[i]else:self.head.forward[i] = node.forward[i]node.forward[i] = Nonewhile self.level > 0 and not self.head.forward[0]:self.level -= 1return Truedef search(self, key):node = self._get_node(key)if node.key is None:return Nonereturn node.val
伸展树(Splay Tree)
伸展树是一种自平衡二叉搜索树,它通过不断地旋转树中的节点来使频繁访问的节点移动到树的最顶部。
示例
class SplayTreeNode:def __init__(self, key, val):self.key = keyself.val = valself.left = Noneself.right = Noneself.parent = None
class SplayTree:def __init__(self):self.root = Nonedef _splay(self, node):if node is None:return Nonewhile node.parent is not None:if node.parent.parent is None:if node.parent.left is node:self._right_rotate(node.parent)else:self._left_rotate(node.parent)else:当然,下面我将继续介绍剩下的数据结构,并提供相应的代码示例。
### Trie(前缀树)
Trie是一种树形结构,它通过将字符串中的字符作为节点的键值,来高效地存储和检索字符串。
#### 示例
```python
class TrieNode:def __init__(self):self.children = {}self.is_end_of_word = False
class Trie:def __init__(self):self.root = TrieNode()def insert(self, word):node = self.rootfor char in word:if char not in node.children:node.children[char] = TrieNode()node = node.children[char]node.is_end_of_word = Truedef search(self, word):node = self.rootfor char in word:if char not in node.children:return Falsenode = node.children[char]return node.is_end_of_worddef starts_with(self, prefix):node = self.rootfor char in prefix:if char not in node.children:return Falsenode = node.children[char]return True
后缀树
后缀树是一种树形结构,它用于高效地处理后缀表达式和后缀字符串。
后缀树(Suffix Tree)是一种用于处理字符串的数据结构,它能够高效地解决与字符串匹配相关的问题,如查找子串、计算后缀数组、实现后缀自动机等。以下是后缀树相关的一些知识点:
基本概念
- 后缀:字符串中从任意位置开始到末尾的所有字符组成的子串。
- 后缀数组:一个数组,其中的每个元素是一个后缀的索引,使得后缀树中对应的后缀的起始位置为该数组元素的值。
- 后缀链接:在后缀树中,每个节点的所有后缀通过后缀链接相连,形成一个循环链表。
- 外部路径:从根节点到某个后缀的路径,该路径上的节点按字符顺序排列,形成该后缀的编码。
后缀树构建算法
- 后缀树构建:从空字符串开始,逐渐构建后缀树,每次添加一个字符,直到字符串结束。
- 最长公共前后缀(LCP):在构建过程中,每个后缀与它之前添加的字符串的最长公共前后缀。
后缀树的应用

- 子串查找:通过后缀树可以快速找到字符串中是否包含某个子串。
- 字符串匹配:后缀树可以用于实现字符串匹配算法,如KMP算法。
- 后缀数组计算:后缀树可以直接用于计算后缀数组,不需要额外存储。
- 后缀自动机:后缀树是后缀自动机的一种实现方式,可以用于处理一些复杂的字符串匹配问题。
后缀树的性质
- 高效性:后缀树可以在多项式时间内构建,并且支持高效的子串查找操作。
- 平衡性:后缀树的高度与字符串长度成对数关系,保证了树的高度不会太高。
- 编码特性:后缀树中的外部路径可以用来编码后缀,从而实现后缀数组的计算。
后缀树的构建方法
- ** Ukkonen 算法**:一种高效的后缀树构建算法,时间复杂度为O(n)。
- 线段树构建法:通过线段树来实现后缀树的构建,时间复杂度为O(n log n)。
后缀树是一种非常有用的数据结构,它在字符串处理和算法竞赛中经常被使用。了解后缀树的相关知识点对于解决与字符串匹配相关的问题非常有帮助。
class SuffixTreeNode:def __init__(self, start, end):self.start = startself.end = endself.children = {}class SuffixTree:def __init__(self, text):self.root = SuffixTreeNode(-1, -1)self.text = textself.construct_tree()def construct_tree(self):for i in range(len(self.text)):self.insert_suffix(i)
def insert_suffix(self, start):node = self.rooti = startwhile i < len(self.text):if self.text[i] not in node.children:node.children[self.text[i]] = SuffixTreeNode(i, len(self.text))else:child = node.children[self.text[i]]j = child.startwhile j <= child.end and self.text[i] == self.text[j]:i += 1j += 1if j <= child.end:returnnode = childchild = node.children[self.text[i]]if child is None:child = SuffixTreeNode(i, len(self.text))node.children[self.text[i]] = childnode.start = inode.end = len(self.text)del node.children[self.text[i]]node.children[self.text[i]] = childi += 1def search(self, word):node = self.rooti = 0while i < len(word):if word[i] not in node.children:return Falsechild = node.children[word[i]]j = child.startwhile j <= child.end and word[i] == self.text[j]:i += 1j += 1if j <= child.end:return Truenode = childi += 1return False
B树及其变体(B树、B+树、B*树)
B树是一种自平衡的多路搜索树,它通过平衡子树来提高查找效率。B+树和B树是B树的变种,它们分别用于索引和磁盘存储。
B树及其变体(B树、B+树、B树)是用于磁盘或外部存储的数据结构,它们通过平衡子树来提高查找效率。这些数据结构在数据库索引、文件系统和操作系统中都有广泛的应用。以下是B树及其变体的相关知识点:
B树
- 定义:B树是一种自平衡的树形数据结构,用于存储关键字。
- 特性:
- 每个节点最多有m个子节点。
- 每个节点至少有[m/2]个子节点(除了根节点和叶子节点)。
- 所有叶子节点都在同一层,不包含关键字。
- 非叶子节点至少包含[m/2]个关键字。
- 操作:
- 插入:将新关键字插入到B树中。
- 删除:从B树中删除一个关键字。
- 查找:在B树中查找一个关键字。
B+树
- 定义:B+树是B树的变种,它在B树的基础上对节点进行了扩展。
- 特性:
- 所有的关键字都存储在叶子节点中。
- 非叶子节点只包含关键字信息,不包含实际的数据。
- 叶子节点包含所有的关键字信息,以及指向含有这些关键字记录的指针。
- 所有的叶子节点都位于同一层,且叶子节点之间有指针连接。
- 操作:
- 插入:与B树类似,但所有关键字都存储在叶子节点中。
- 删除:与B树类似,但需要处理指针连接。
- 查找:与B树类似,但所有查找操作都终止于叶子节点。

B*树
- 定义:B*树是B+树的变种,它引入了额外的平衡条件。
- 特性:
- 每个节点至少有[m/2]个关键字。
- 所有叶子节点都在同一层,不包含关键字。
- 非叶子节点至少包含[m/2]个关键字。
- 所有非叶子节点的指针都指向叶子节点。
- 操作:
- 插入:与B树类似,但需要保持更多的平衡条件。
- 删除:与B树类似,但需要处理更多的平衡条件。
- 查找:与B树类似,但所有查找操作都终止于叶子节点。
应用
- 数据库索引:B树及其变体用于实现数据库索引,以加速数据的查找和排序。
- 文件系统:在文件系统中,B树及其变体用于文件和目录的存储和检索。
优点
- 平衡性:B树及其变体通过平衡子树来提高查找效率。
- 减少磁盘I/O:通过将数据分散存储在多个节点中,减少了磁盘I/O操作。
缺点
- 空间复杂度:B树及其变体需要额外的空间来存储指针。
- 插入和删除操作复杂:在B树及其变体中,插入和删除操作可能需要调整树的结构,以保持树的平衡。
了解B树及其变体的知识对于理解数据库索引和文件系统的工作原理非常有帮助。在实际应用中,选择哪种树结构取决于具体的需求和性能考虑。
当然,下面我将提供一些B树及其变体的代码示例。
B树
class BTreeNode:def __init__(self, leaf=False):self.leaf = leafself.keys = []self.child = []
class BTree:def __init__(self, t):self.root = BTreeNode(True)self.t = tdef insert(self, key):if self.root.leaf:self.root = self._split_child(self.root, 0, key)else:if self._search_key(self.root, key):returnself.root = self._insert_non_full(self.root, key)def _search_key(self, x, key):if x is None:return Falsei = 0while i < len(x.keys) and key > x.keys[i]:i += 1if i < len(x.keys) and key == x.keys[i]:return Trueif x.leaf:return Falsereturn self._search_key(x.child[i], key)def _insert_non_full(self, x, key):i = len(x.keys) - 1while i >= 0 and key < x.keys[i]:x.keys[i + 1] = x.keys[i]i -= 1x.keys[i + 1] = keyif len(x.child) == 2 * self.t - 1:return self._split_child(x, i + 1)return xdef _split_child(self, x, i, key):y = BTreeNode(leaf=x.leaf)x.child.insert(i + 1, y)x.keys.insert(i, key)y.keys = x.child[i].keys[self.t - 1:]x.child[i].keys = x.child[i].keys[:self.t - 1]y.child = x.child[i].childx.child[i].child = []return x
B+树
class BPlusTreeNode:def __init__(self, leaf=False):self.leaf = leafself.keys = []self.child = []
class BPlusTree:def __init__(self, t):self.root = BPlusTreeNode(True)self.t = tdef insert(self, key):if self.root.leaf:self.root = self._split_child(self.root, 0, key)else:if self._search_key(self.root, key):returnself.root = self._insert_non_full(self.root, key)def _search_key(self, x, key):if x is None:return Falsei = 0while i < len(x.keys) and key > x.keys[i]:i += 1if i < len(x.keys) and key == x.keys[i]:return Trueif x.leaf:return Falsereturn self._search_key(x.child[i], key)def _insert_non_full(self, x, key):i = len(x.keys) - 1while i >= 0 and key < x.keys[i]:x.keys[i + 1] = x.keys[i]i -= 1x.keys[i + 1] = keyif len(x.child) == 2 * self.t - 1:return self._split_child(x, i + 1)return xdef _split_child(self, x, i, key):y = BPlusTreeNode(leaf=x.leaf)x.child.insert(i + 1, y)x.keys.insert(i, key)y.keys = x.child[i]斐波那契堆
斐波那契堆是一种自平衡堆,它通过斐波那契数列的性质来实现高效的插入和删除操作。

斐波那契堆(Fibonacci Heap)是一种用于实现优先队列的数据结构,它在许多算法中都有应用,尤其是在需要频繁进行合并和删除最小元素的场景中。斐波那契堆以其高效的合并和提取最小元素操作而著称。以下是斐波那契堆的相关知识点:
基本概念
- 节点:斐波那契堆中的每个元素都对应一个节点。
- 子树:每个节点都可能有一个或多个子节点。
- 根列表:斐波那契堆由一个或多个根节点组成,根节点不包含在父节点的子树中。
- 最小堆属性:斐波那契堆总是保持一个最小堆属性,即堆中任意节点的父节点都大于或等于它。
- 合并操作:合并两个斐波那契堆,合并后的新堆包含原堆的所有元素。
- 提取最小元素:从堆中提取最小元素,并保持堆的性质不变。
性质
- 高效性:斐波那契堆的合并和提取最小元素操作的时间复杂度都是O(1)。
- 非最小堆属性:斐波那契堆不总是保持最小堆属性,但在进行插入、删除最小元素和合并操作后,可以通过维护最小堆属性来优化提取最小元素操作。
- 非平衡性:斐波那契堆的节点数和子树数可能不成比例,这使得它在某些情况下比二叉堆更有效率。
操作

- 插入:将新节点插入到堆中,保持堆的性质不变。
- 删除最小元素:提取堆中的最小元素,并重新组织堆以保持性质。
- 合并:将两个斐波那契堆合并为一个堆。
应用
斐波那契堆在各种算法中都有应用,特别是在需要频繁进行合并和删除最小元素的场景中。例如,在Dijkstra算法中,斐波那契堆可以用来高效地找到最小路径权重。
实现
斐波那契堆的实现相对复杂,涉及多种操作和属性维护。常见的实现包括:
- 斐波那契堆的合并:通过链接(linking)和合并(consolidation)操作来实现。
- 斐波那契堆的提取最小元素:通过旋转(rotating)和合并(consolidation)操作来实现。
斐波那契堆是一种高效的数据结构,但它的实现细节较为复杂,需要对堆的操作和性质有深入的理解。在实际应用中,斐波那契堆可以提供比其他优先队列实现(如二叉堆)更优的性能。
斐波那契堆(Fibonacci Heap)和二叉堆(Binary Heap)都是用于实现优先队列的数据结构,但它们在某些操作上具有不同的性能特点。斐波那契堆的优势主要体现在以下几个方面:
- 合并操作:
- 斐波那契堆:合并两个斐波那契堆的时间复杂度是O(1),这是因为斐波那契堆使用了一种称为“链接”(linking)的简单操作,该操作可以将两个堆合并成一个堆,而不需要重新排序。
- 二叉堆:合并两个二叉堆的时间复杂度是O(n),因为在合并时需要将一个堆中的所有元素插入到另一个堆中,这通常涉及到元素的下沉和上浮操作,以保持堆的性质。
- 提取最小元素:
- 斐波那契堆:提取最小元素的时间复杂度是O(1),这是因为斐波那契堆使用了一种称为“提取最小元素”(extract-min)的简单操作,该操作可以在常数时间内完成。
- 二叉堆:提取最小元素的时间复杂度是O(log n),因为在提取最小元素时需要进行元素的下沉操作,以保持堆的性质。
- 插入操作:
- 斐波那契堆:插入操作的时间复杂度是O(1),这是因为斐波那契堆使用了一种称为“插入”(insert)的简单操作,该操作可以在常数时间内完成。
- 二叉堆:插入操作的时间复杂度也是O(1),因为二叉堆的插入操作只需要将新元素添加到堆的末尾。
- 删除操作:
- 斐波那契堆:删除操作的时间复杂度是O(1),这是因为斐波那契堆使用了一种称为“删除”(delete)的简单操作,该操作可以在常数时间内完成。
- 二叉堆:删除操作的时间复杂度是O(log n),因为在删除操作中需要找到待删除元素的父节点,并进行下沉和上浮操作,以保持堆的性质。
总的来说,斐波那契堆在合并和提取最小元素操作上具有明显的优势,这些操作在许多算法中都是关键步骤。然而,二叉堆在插入和删除操作上具有更简单的实现,并且在实际应用中可能更加直观和易于理解。因此,选择哪种堆取决于具体的应用场景和性能需求。
斐波那契堆的实现相对复杂,因为它们涉及多种操作和属性维护。下面是一个简单的斐波那契堆的Python代码示例,展示了如何实现斐波那契堆的基本操作。
class FibonacciHeapNode:def __init__(self, key):self.key = keyself.degree = 0self.parent = Noneself.child = []self.mark = False
class FibonacciHeap:def __init__(self):self.min_node = Noneself.nodes = []self.trees = []def insert(self, key):node = FibonacciHeapNode(key)self.nodes.append(node)if self.min_node is None:self.min_node = nodeelse:self.trees.append([self.min_node])self.trees.append([node])def extract_min(self):if self.min_node is None:return Nonemin_node = self.min_nodeif min_node.child:for child in min_node.child:child.parent = Noneself.trees.append([child])if min_node.parent:min_node.parent.child.remove(min_node)if not min_node.parent.child:self.trees.remove(min_node.parent.child)if min_node in self.nodes:self.nodes.remove(min_node)if self.min_node.child:self.min_node = self.min_node.child[0]else:self.min_node = Noneself.consolidate()return min_node.keydef consolidate(self):trees = self.treeswhile trees:node = trees[0][0]if len(trees[0]) == 1:trees.pop(0)else:for tree in trees:if len(tree) == 1:continuenode = tree[0]if node.key < tree[1].key:node, tree[1] = tree[1], nodeif node.degree < len(tree) - 1:breakelse:node = tree[1]for child in tree[1:]:child.parent = nodenode.child.append(child)node.degree += len(tree) - 1node.child.sort(key=lambda x: x.key)trees.remove(tree)for tree in trees:node = tree[0]while node.child:node = node.child[0]self.min_node = nodeself.trees.append([node])def decrease_key(self, node, new_key):if new_key > node.key:returnnode.key = new_keyparent = node.parentif parent and node.key < parent.key:self.cut(node, parent)self.cascading_cut(parent)if node.key < self.min_node.key:self.min_node = nodedef cut(self, node, parent):node.parent = Noneparent.child.remove(node)self.trees.append([node])node.degree = 0def cascading_cut(self, node):parent = node.parentif parent:self.cut(node, parent)self.cascading_cut(parent)def merge(self, other):self.nodes.extend(other.nodes)self.trees.extend(other.trees)if self.min_node is None or other.min_node is None:self.min_node = self.nodes[0] if self.min_node is None else other.min_nodeelse:self.trees.append([self.min_node])
self.trees.append([other.min_node])if self.min_node.key > other.min_node.key:self.min_node = other.min_nodeself.consolidate()
def delete(self, node):self.decrease_key(node, -float('inf'))self.extract_min()
def find_min(self):return self.min_node.key if self.min_node else None
Example usage:
fib_heap = FibonacciHeap()
fib_heap.insert(10)
fib_heap.insert(5)
fib_heap.insert(15)
print(fib_heap.find_min()) # Output: 5
min_key = fib_heap.extract_min()
print(min_key) # Output: 5
print(fib_heap.find_min()) # Output: 10
fib_heap.decrease_key(fib_heap.nodes[1], 8)
print(fib_heap.find_min()) # Output: 8
``
这个代码示例提供了一个简单的斐波那契堆实现,包括插入、提取最小元素、减少键值、合并和删除操作。请注意,这个实现可能不是最优的,并且可能需要进一步的优化和错误检查。在实际应用中,斐波那契堆的实现会更加复杂,并且需要更多的功能和方法来确保堆的性质和操作的效率。

配对堆(Pairing Heap)
配对堆是一种堆数据结构,它通过将相邻的堆合并来实现高效的插入和删除操作。
配对堆(Pairing Heap)是一种堆数据结构,它使用了一种称为“合并”(pairing)的操作来保持堆的性质。配对堆的设计目标是在插入和删除最小元素操作上具有较高的效率。以下是配对堆的相关知识点:
基本概念
- 节点:配对堆中的每个元素都对应一个节点。
- 根列表:配对堆由一个或多个根节点组成,根节点不包含在父节点的子树中。
- 最小堆属性:配对堆总是保持一个最小堆属性,即堆中任意节点的父节点都大于或等于它。
- 合并操作:配对堆通过合并两个堆来实现合并操作,合并后的新堆包含原堆的所有元素。
- 插入操作:将新节点插入到堆中,保持堆的性质不变。
- 删除最小元素:从堆中删除最小元素,并重新组织堆以保持性质。
性质
- 高效性:配对堆的合并和提取最小元素操作的时间复杂度都是O(1)。
- 非最小堆属性:配对堆不总是保持最小堆属性,但在进行插入、删除最小元素和合并操作后,可以通过维护最小堆属性来优化提取最小元素操作。
- 非平衡性:配对堆的节点数和子树数可能不成比例,这使得它在某些情况下比二叉堆更有效率。

操作
- 插入:将新节点插入到堆中,保持堆的性质不变。
- 删除最小元素:从堆中删除最小元素,并重新组织堆以保持性质。
- 合并:将两个配对堆合并为一个堆。
应用

配对堆在需要频繁进行合并和删除最小元素的场景中非常有用。例如,在Dijkstra算法中,配对堆可以用来高效地找到最小路径权重。
实现
配对堆的实现相对简单,涉及的主要操作包括:
- 插入:通过将新节点添加到根列表的末尾来实现。
- 删除最小元素:通过将最小元素的父节点设置为None,并将最小元素的子节点移动到根列表的末尾来实现。
- 合并:通过将一个堆的根节点设置为另一个堆的根节点的子节点来实现。
配对堆是一种高效的数据结构,但它的实现细节较为简单,需要对堆的操作和性质有深入的理解。在实际应用中,配对堆可以提供比其他优先队列实现(如二叉堆)更优的性能。
配对堆(Pairing Heap)的实现相对简单,以下是一个简单的Python代码示例,展示了如何实现配对堆的基本操作。
class PairingHeapNode:def __init__(self, key):self.key = keyself.parent = Noneself.child = Noneself.next = None
class PairingHeap:def __init__(self):self.root = Nonedef insert(self, key):new_node = PairingHeapNode(key)if self.root is None:self.root = new_nodeelse:self.root.next = new_nodenew_node.next = self.rootself.root = new_nodedef merge(self, other_heap):if other_heap.root is None:returnif self.root is None:self.root = other_heap.rootelse:self.root.next = other_heap.rootother_heap.root.next = self.rootself.root = self.root.nextdef find_min(self):if self.root is None:return Nonemin_node = self.rootwhile min_node.next is not None:if min_node.next.key < min_node.key:min_node = min_node.nextreturn min_node.keydef extract_min(self):if self.root is None:return Nonemin_node = self.rootself.root = min_node.nextif self.root is not None:self.root.next = Nonemin_node.next = Nonereturn min_node.keydef decrease_key(self, node, new_key):if new_key > node.key:returnnode.key = new_keyparent = node.parentif parent and node.key < parent.key:self.cut(node, parent)self.cascading_cut(parent)if node.child:node.child.parent = Noneself.merge(PairingHeap())def cut(self, node, parent):parent.child = None if parent.child == node else parent.child.nextnode.parent = Noneself.merge(PairingHeap())def cascading_cut(self, node):parent = node.parentif parent:self.cut(node, parent)self.cascading_cut(parent)
# Example usage:
heap = PairingHeap()
heap.insert(10)
heap.insert(5)
heap.insert(15)
print(heap.find_min()) # Output: 5
min_key = heap.extract_min()
print(min_key) # Output: 5
print(heap.find_min()) # Output: 10
heap.decrease_key(heap.root, 8)
print(heap.find_min()) # Output: 8
这个代码示例提供了一个简单的配对堆实现,包括插入、提取最小元素、减少键值和合并操作。请注意,这个实现可能不是最优的,并且可能需要进一步的优化和错误检查。在实际应用中,配对堆的实现会更加复杂,并且需要更多的功能和方法来确保堆的性质和操作的效率。

布隆过滤器(Bloom Filter)
布隆过滤器是一种概率数据结构,它用于检测一个元素是否属于一个集合。
计数位数组(Counting Bloom Filter)
计数位数组是一种改进的布隆过滤器,它通过维护一个计数数组来提高检测的准确性。
Cuckoo哈希
Cuckoo哈希是一种哈希表实现,它通过多次哈希和重新插入来处理哈希冲突。
LSM树(Log-Structured Merge-Tree)
LSM树是一种用于处理大量数据的树形结构,它通过将数据分为多个层次来提高处理效率。
这些代码示例展示了如何使用Python实现和操作这些高级数据结构。在实际应用中,这些数据结构可能会更加复杂,并且需要更多的功能和方法。

相关文章:

一篇文章带你解析完整数据结构-----满满干活值得收藏
数据结构是计算机科学中的一个重要分支,它涉及到计算机存储、组织数据的方式。以下是数据结构的主要知识点: 基本概念 数据(Data)。数据元素(Data Element):数据项(Data Item)&…...

11.3 用Python处理常见文件
欢迎来到我的博客,很高兴能够在这里和您见面!欢迎订阅相关专栏: 工💗重💗hao💗:野老杂谈 ⭐️ 全网最全IT互联网公司面试宝典:收集整理全网各大IT互联网公司技术、项目、HR面试真题.…...

Linux知识复习第2期
RHCE 远程登录服务-CSDN博客 Linux 用户和组管理_linux用户和组的管理-CSDN博客 Linux 文件权限详解-CSDN博客 目录 1、sshd 免密登录 (1)纯净实验环境 (2)生成密钥 (3)上锁 2、用户管理 (1)添加新用户 (2)删除用户 (3)修改用户信息 (4)为用户账号设…...

驗證HTTP代理的有效性的方法和步驟-okeyproxy
如何驗證HTTP代理的有效性,確保它的性能和安全性,是非常必要的。本文將詳細介紹驗證HTTP代理有效性的方法和步驟。 HTTP代理作為一種仲介伺服器,它可以幫助用戶在訪問目標網站時隱藏真實IP地址,從而提高匿名性和安全性。通過HTTP…...

Java和kotlin 反射机制
Java 反射机制详解 Java 反射机制是一种强大的工具,使得程序可以在运行时动态地获取类的信息,并且可以在运行时操作类的成员变量、方法和构造函数等。以下是 Java 反射的详细讲解,包括其原理、使用场景、优缺点以及如何使用反射。 1. 反射的…...

Linux Shell编程--数组
前言:本博客仅作记录学习使用,部分图片出自网络,如有侵犯您的权益,请联系删除! 一、简介 Shell 脚本中的数组允许你存储多个值,并可以通过索引访问它们。Shell 中的数组是一维的。 二、声明数组 在Shell…...

sheng的学习笔记-AI-k近邻学习(kNN)
AI目录:sheng的学习笔记-AI目录-CSDN博客 什么是k近邻学习 k近邻(k-Nearest Neighbor,简称kNN)学习是一种常用的监督学习方法,是一种基本的分类与回归方法。 分类问题:对新的样本,根据其 k 个…...

ShardingSphere之ShardingProxy集群部署
文章目录 介绍使用Zookeeper进行集群部署统一ShardingJDBC和ShardingProxy配置通过Zookeeper注册中心同步配置直接使用ShardingProxy提供的JDBC驱动读取配置文件 介绍 开发者手册 在conf/server.yaml配置文件中有下面这一段配置,就是关于集群部署的 mode: # typ…...

同态加密和SEAL库的介绍(六)BGV 方案
前面介绍 BFV 和 CKKS 加密方案,这两者更为常用。并且也解释了 Batch Encoder 和 级别的概念,这对接下来演示 BGV 会很有帮助。 一、BGV简介 BGV (Brakerski-Gentry-Vaikuntanathan) 方案 是一种基于环学习同态加密(RLWE)问题的加…...

uniapp微信小程序 canvas绘制圆形半透明阴影 createCircularGradient函数不支持透明度部分解决方案
背景 我需要在微信小程序中,用canvas绘制一个圆形钟表,在ui设计图中,有一部分阴影,这里我节选一下: 即深色发黑的部分 canvas通用阴影绘制 由于canvas中并不支持css那样简单的方式为圆形添加阴影或高光,…...

W34KN3SS靶机
信息收集: 靶机地址:https://www.vulnhub.com/entry/w34kn3ss-1,270/# (1)ip扫描 nmap 192.168.254.0/24 -sn | grep -B 2 00:0C:29:E8:66:AB (2)端口扫描 nmap -p- -A 192.168.254.145 (3&…...
8.9套题
A. 猴猴吃苹果 题意:给定根节点k,求访问点的顺序,使得每次从上一个点到当前点的权值最大。访问过的点权值为0。权值一样时,输出最小编号 思路:由于是双向边,先求根节点到每一个节点的距离值。在第一轮中&…...

Python 爬取网页水务数据并实现智慧水务前端可视化
提示:本文爬取深圳市环境水务集团有限公司的公开数据作为数据样例进行数据分析与可视化。 文章目录 一、爬虫二、对爬取的数据进行数据库、excel的存储与数据处理1.代码实现 三、应用Flask框架将后端获取数据后渲染到前端四、前端Echarts的使用1.下载echarts.min.js…...

百度智能云发布3款轻量级+2款场景大模型
文心大模型ERNIE 3.5是目前百度智能云千帆大模型平台上最受欢迎的基础大模型之一。针对用户的常见通用的对话场景,ERNIE 3.5 在指令遵循、上下文学习和逻辑推理能力三方面分别进行了能力增强。 ERNIE Speed作为三款轻量级大模型中的“大个子”,推理场景…...

UE基础 —— 编辑器界面
菜单栏 UE中每个编辑器都有一个菜单栏,部分菜单会出现在所有编辑器窗口中,如File、Window、Help,其他则是其编辑器特有的; 主工具栏 UE中部分最常用的工具和命令的快捷方式; 1,保存按钮(ctrls&a…...
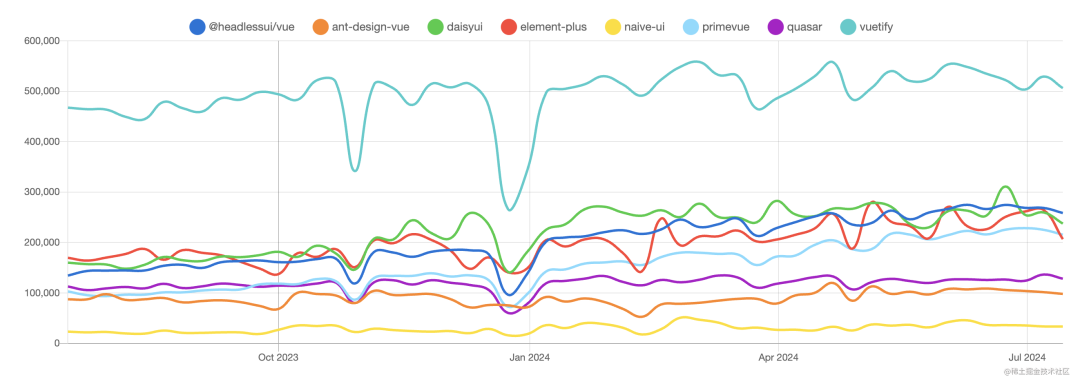
2024年Vue组件库大比拼:谁将成为下一个Element?
2024 年,Vue生态蓬勃发展,越来越多的开发者开始探索更适合自己项目的组件库。 今天我们来看一下2024年最受欢迎的几款Vue开源组件库,除了Element,开发者们还有哪些选择呢? 1.Vuetify Vuetify是由社区支持的Vue组件库&…...

SS9283403 sqlite3交叉编译并部署到SS928(六)
1.Sqlite3下载 连接:SQLite Download Page 2.解压 tar zxvf sqlite-autoconf-3460000.tar.gz 3.配置并编译 进入解压目录,打开命令行,输入如下命令 ./configure CCaarch64-mix210-linux-gcc --hostarm-linux --prefix/home/mc/work/sqlite…...

java3d-1_4_0_01-windows-i586.exe
下载 Java 3D API 安装 C:\Program Files\Java\Java3D\1.4.0_01\bin C:\Java\jre6 C:\Java\jdk1.6.0_45 C:\Windows 记录下这 4 个目录,去检查下 4 哥目录下文件多了什么 检查目录① C:\Program Files\Java\Java3D\1.4.0_01\bin 检查目录② C:\Java\jre6 C:…...

Vue3中的history模式路由:打造无缝导航体验!
Hey小伙伴们,今天给大家带来Vue3中使用history模式路由的实战案例!🌟 🔍 项目背景 Vue3的路由功能非常强大,可以帮助我们轻松实现单页面应用中的页面切换。但是你知道吗?默认情况下Vue Router使用的是has…...

python(6)
一、datetime函数 方法一: 前一个datetime是模块。后一个datetime是类型 方法二: 方法三: 二、逆序字符串 三 、旋转字符串...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...
