代码随想录第十天(28)
文章目录
- 28. 找出字符串中第一个匹配项的下标
- 看答案
- KMP
- next数组(前缀表)
- 最长公共前后缀
- 如何计算前缀表
- 前缀表与next数组
- 时间复杂度分析
28. 找出字符串中第一个匹配项的下标
莫得思路……好久没做题,都已经忘得差不多了
看答案
其实就是自己写一个String的indexOf函数,它的作用是返回某个字符串在另一个字符串中首次出现的位置。
利用的思想是KMP
KMP
例子:
要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf。
KMP主要应用在字符串匹配上。
KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
next数组(前缀表)
next数组就是一个前缀表(prefix table)。
前缀表有什么作用呢?
前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
那么什么是前缀表:记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
最长公共前后缀
文章中字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。
正确理解什么是前缀什么是后缀很重要!
所以字符串a的最长相等前后缀为0。 字符串aa的最长相等前后缀为1。 字符串aaa的最长相等前后缀为2。 等等…
匹配的过程在下标5的地方遇到不匹配,模式串是指向f:
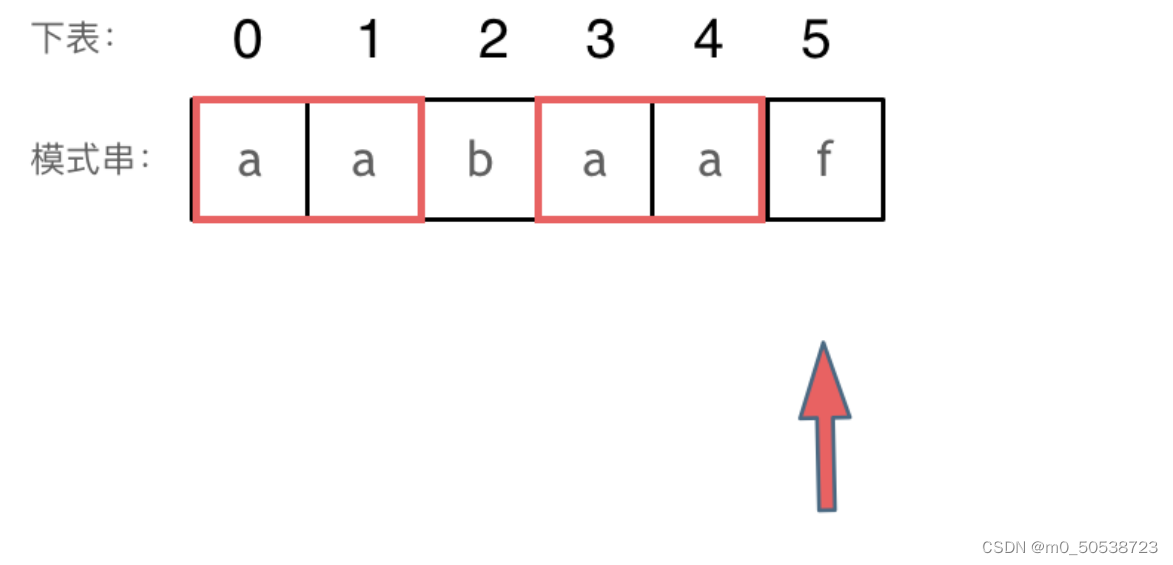
然后应该找到了下标2,指向b,继续匹配:如图:
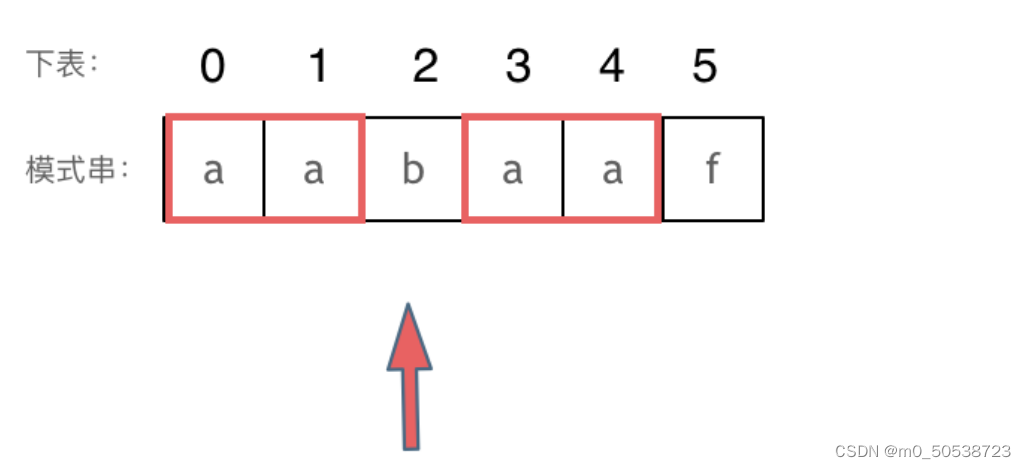
以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面重新匹配就可以了。
所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
如何计算前缀表
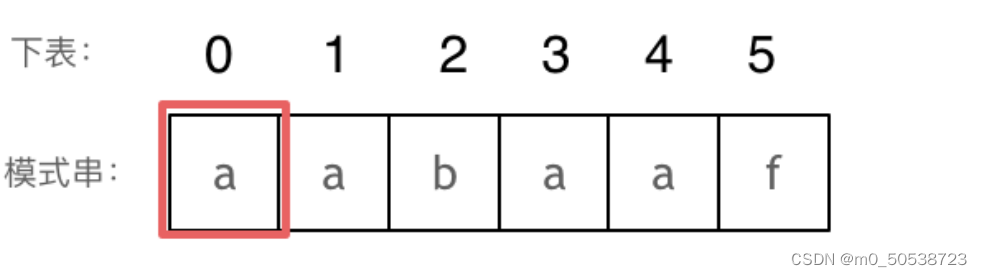
长度为前1个字符的子串a,最长相同前后缀的长度为0。
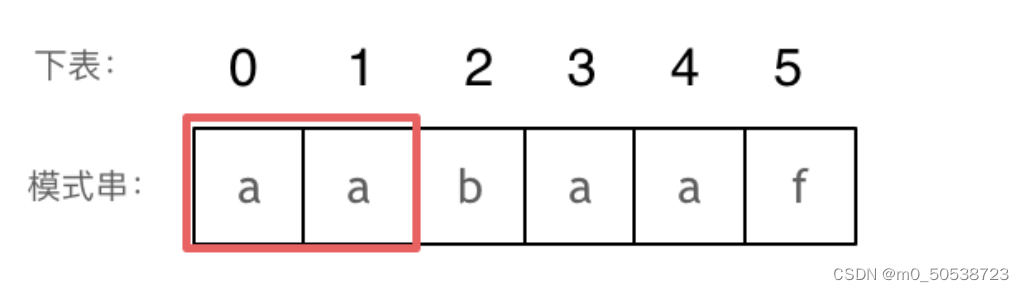
长度为前2个字符的子串aa,最长相同前后缀的长度为1。
长度为前3个字符的子串aab,最长相同前后缀的长度为0。
以此类推: 长度为前4个字符的子串aaba,最长相同前后缀的长度为1。 长度为前5个字符的子串aabaa,最长相同前后缀的长度为2。 长度为前6个字符的子串aabaaf,最长相同前后缀的长度为0。
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
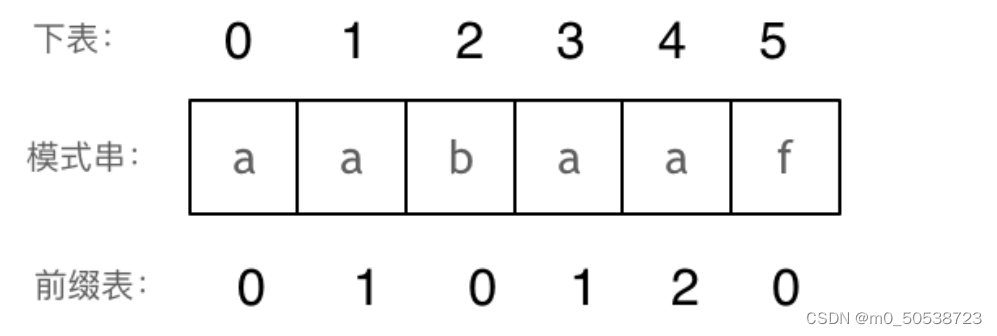
找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
然后移动到,从前一个字符处开始,它对应的前缀表是多少,就向前移多少个位置(不包括前一个元素本身),所以移动到b处
其实这里移动到的位置就是前缀表的元素代表的位置,不用前移多少个元素,比如aabaaf中,f处不匹配,应该移动到它的前一个元素a对应的前缀表元素所指的位置,即字符串下标为2的元素处,即b。
前缀表与next数组
很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
其实这并不涉及到KMP的原理,而是具体实现,next数组既可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。
时间复杂度分析
其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),之前还要单独生成next数组,时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
暴力的解法显而易见是O(n × m),所以KMP在字符串匹配中极大地提高了搜索的效率。
class Solution {public int strStr(String haystack, String needle) {int[] next=new int[needle.length()];next[0]=0;getNext(next,needle);int j=0;for(int i=0;i<haystack.length();i++){//这里的i是从0开始,此时的目的是要将//长的字符串和短的字符串从0号位置开始比较while(j>0&&haystack.charAt(i)!=needle.charAt(j)){j=next[j-1];}if(haystack.charAt(i)==needle.charAt(j)){j++;}if(j==needle.length()){return i-needle.length()+1;}}return -1;}//获得next数组public void getNext(int[] next,String s){int j=0;for(int i=1;i<s.length();i++){//因为要得到前后相等的公共字符串,而next的0位置的元素//一定是0,所以i取1,也就是从next数组的1号元素开始填充while(j>0&&s.charAt(i)!=s.charAt(j)){j=next[j-1];//回退到前个元素的next数组处}if(s.charAt(i)==s.charAt(j)){j++;}next[i]=j;}}
}
相关文章:

代码随想录第十天(28)
文章目录28. 找出字符串中第一个匹配项的下标看答案KMPnext数组(前缀表)最长公共前后缀如何计算前缀表前缀表与next数组时间复杂度分析28. 找出字符串中第一个匹配项的下标 莫得思路……好久没做题,都已经忘得差不多了 看答案 其实就是自己…...
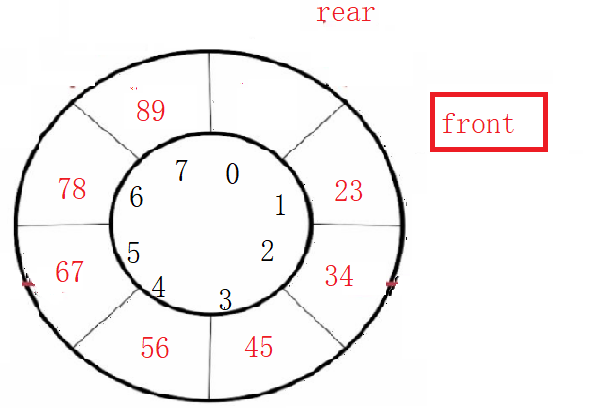
循环队列来了解一下!!
笔者在之前的一篇文章,详细的介绍了:队列之单向链表与双向链表的模拟实现:https://blog.csdn.net/weixin_64308540/article/details/128742090?spm1001.2014.3001.5502 感兴趣的各位老铁,可以参考一下啦!下面进入循环…...
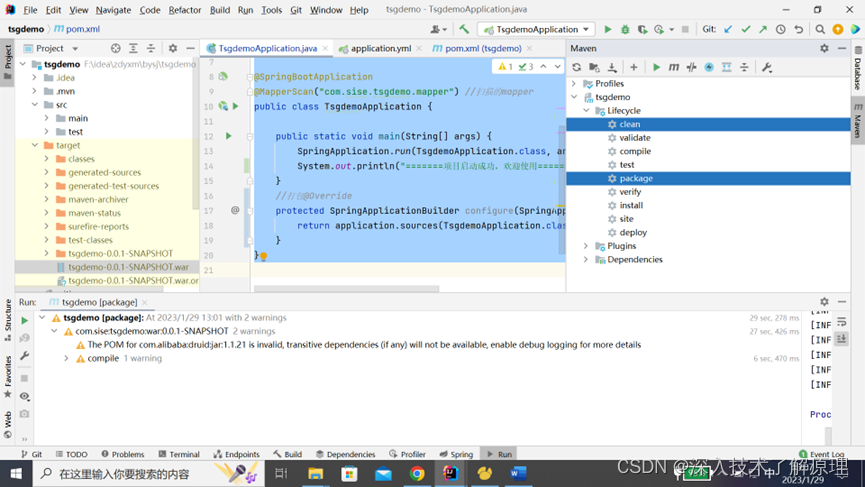
Idea打包springboot项目war包,测试通过
pom.xml文件 <!--包名以及版本号,这个是打包时候使用,版本可写可不写,建议写有利于维护系统--> <artifactId>tsgdemo</artifactId> <version>0.0.1-SNAPSHOT</version> <!--打包形式--> <packaging&…...

python+django高校师生健康信息管理系统pycharm
管理员功能模块 4.1登录页面 管理员登录,通过填写注册时输入的用户名、密码、角色进行登录,如图所示。 4.2系统首页 管理员登录进入师生健康信息管理系统可以查看个人中心、学生管理、教师管理、数据收集管理、问卷分类管理、疫情问卷管理、问卷调查管理…...
CUDA中的流序内存分配
文章目录CUDA中的流序内存分配1. Introduction2. Query for Support3. API Fundamentals (cudaMallocAsync and cudaFreeAsync)4. Memory Pools and the cudaMemPool_t注意:设备的内存池当前将是该设备的本地。因此,在不指定内存池的情况下进行分配将始终…...

开源、低成本的 Xilinx FPGA 下载器(高速30MHz)
目前主流的Xilinx下载器主要有两种:一种是Xilinx官方出品的Xilinx Platfom Cable USB,还有一个就是Xilinx的合作伙伴Digilent开发的JTAG-HS3 Programming Cable。 JTAG-HS系列最大支持30MHz下载速度,基于FTDI的FT2232方案。 JTAG-HS系列对比…...
Maven专题总结
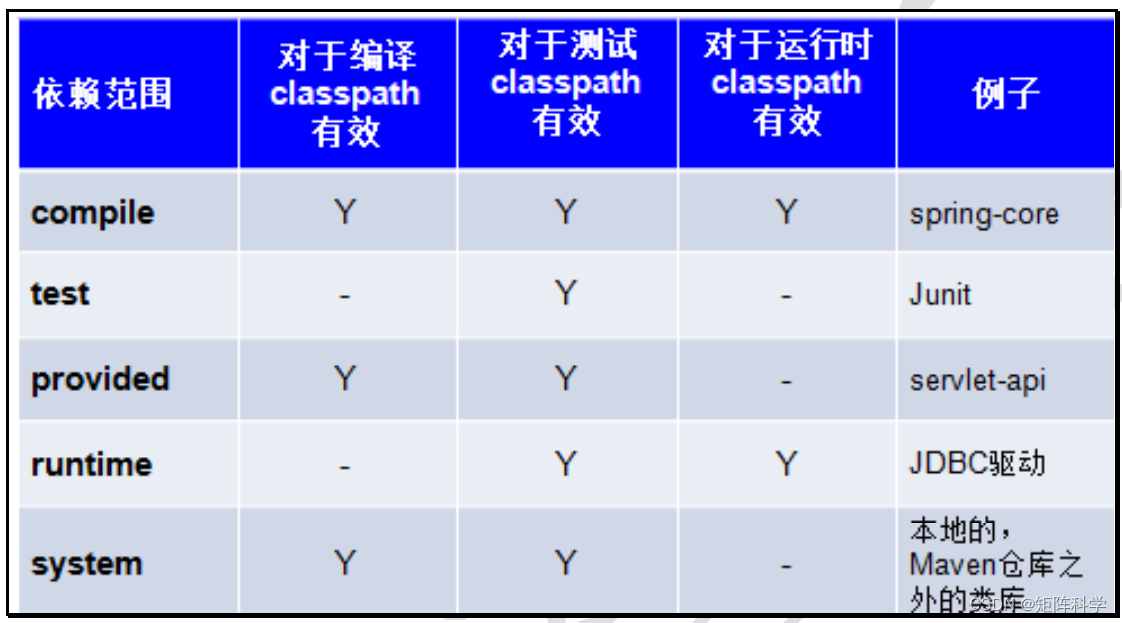
1. 什么是Maven Maven 是一个项目管理工具,它包含了一个项目对象模型 (POM: Project Object Model),一组标准集合,一个项目生命周期(Project Lifecycle),一个依赖管理系统(Dependency Management System),和…...
谷粒商城--SPU和SKU
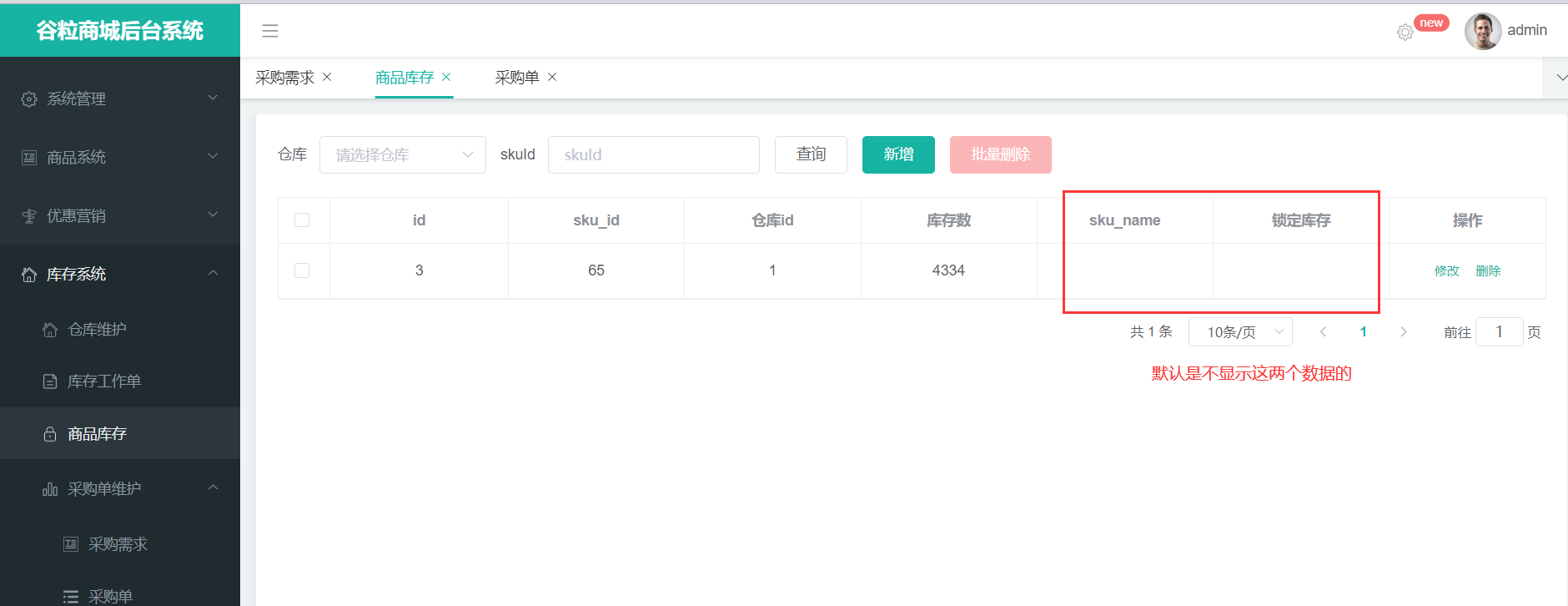
目录 1.SPU和SKU概念 2.表的关系理解 3.导入前端代码 4.完善后端接口 5.属性分组详情 6.规格参数详情 7. 销售属性详情 8.分组与属性关联 9.发布商品 10.仓库服务 1.SPU和SKU概念 SPU:standard product unit(标准化产品单元):是商品信息聚合的…...
二叉树OJ题(上)
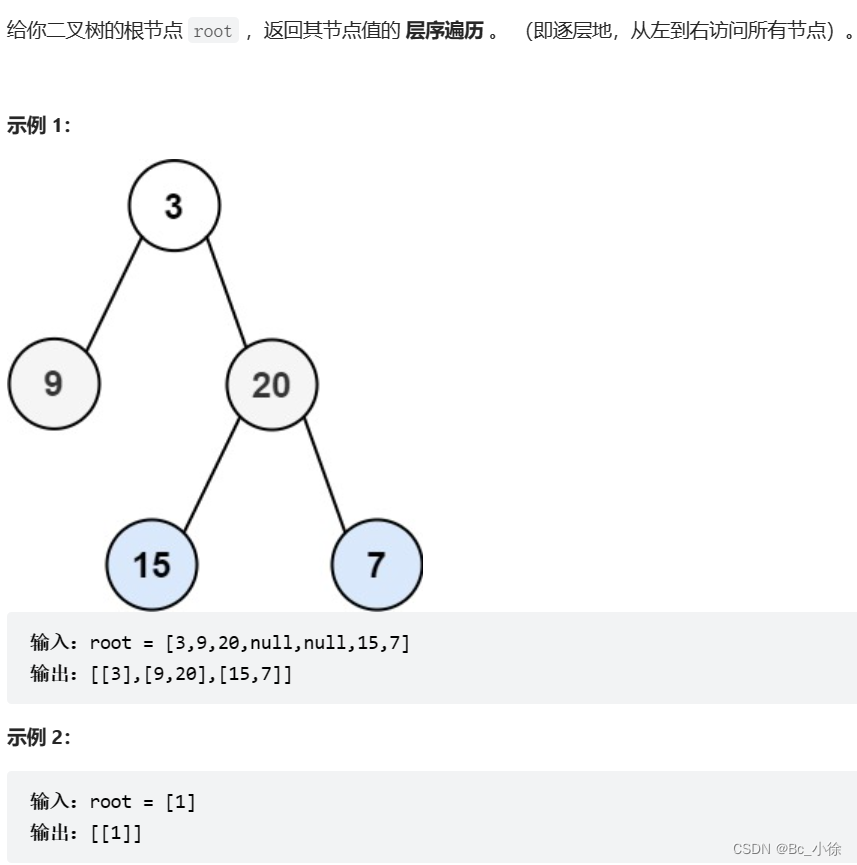
✅每日一练:100. 相同的树 - 力扣(LeetCode) 题目的意思是俩棵树的结构不仅要相同,而且每个节点的值还要相同,如果满足上面2个条件,则成立! 解题思路: 从三个方面去考虑࿱…...

第一章 PDF语法
第一章 PDF语法PDF ObjectsNull ObjectsBoolean ObjectsNumeric ObjectsName ObjectsString ObjectsArray ObjectsDictionary ObjectsName treesNumber treesStream ObjectsDirect versus Indirect ObjectsFile StructureWhite-SpaceThe Four Sections of a PDFHeaderTrailerBo…...
IntelliJ IDEA 创建JavaFX项目运行
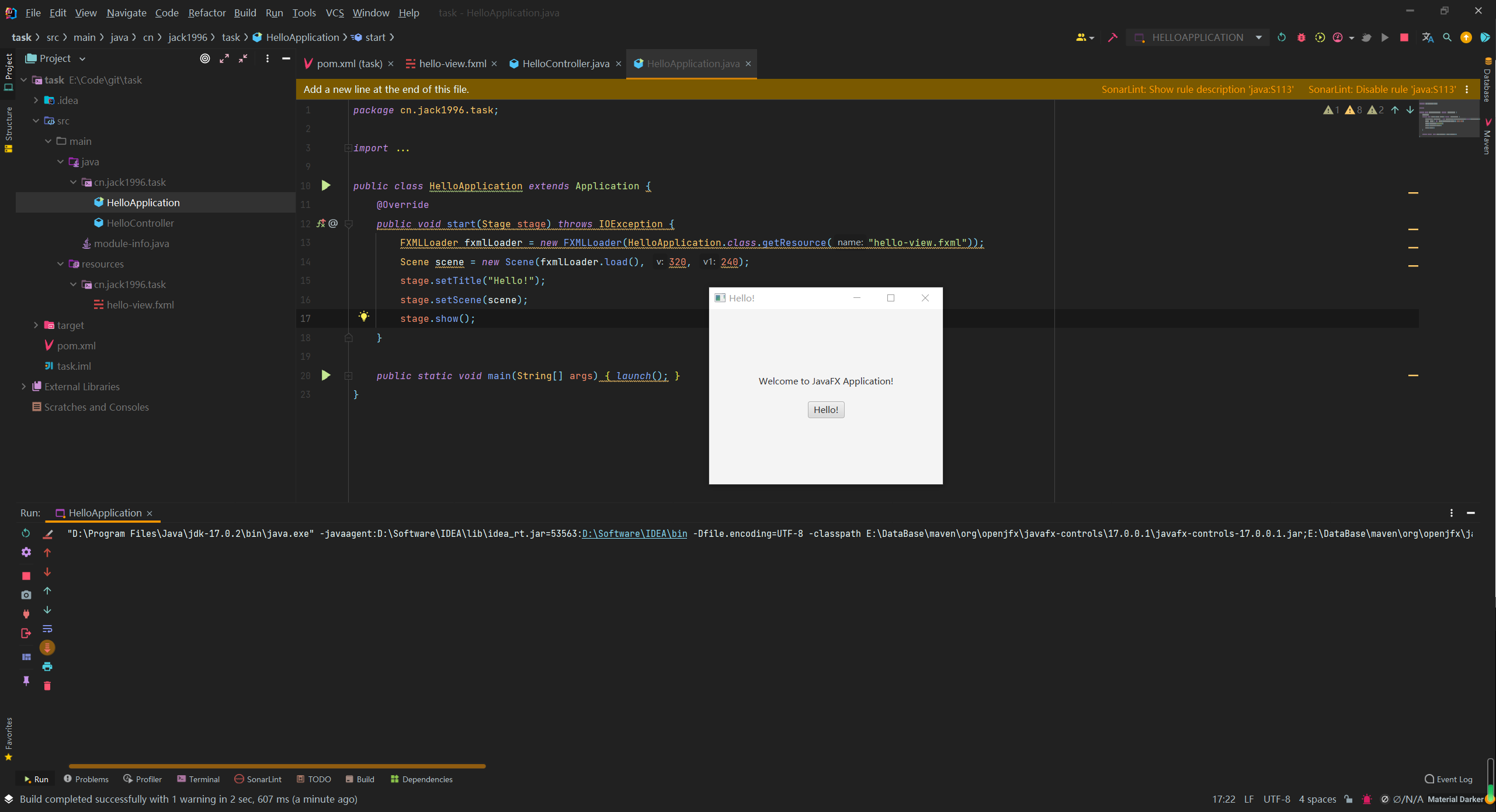
IntelliJ IDEA 创建JavaFX项目运行JavaFX官网文档:https://openjfx.io/openjfx-docs/ JavaFX 2008年12月05日诞生,是一个开源的下一代客户端应用程序平台,适用于基于 Java 构建的桌面、移动和嵌入式系统。这是许多个人和公司的协作努力&#…...

IC封装常见形式
参考:https://blog.csdn.net/dhs888888/article/details/127673300?utm_mediumdistribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-127673300-blog-115610343.pc_relevant_multi_platform_whitelistv4&spm1001.2101.3001.4242…...

Linux通配符、转义符讲解
目录 通配符 通过通配符定义匹配条件 转义符 将所有的逻辑操作符都转换成字符 通配符 通过通配符定义匹配条件 * 任意字符都可以通配(也可以匹配空值) ? 匹配单个字符 [a-z] 匹配单个的小写英文字母 [A-Z] 匹配单个的大写英文…...

[OpenMMLab]提交pr时所需的git操作
git开发流程 准备工作 作为一个开发者,fork一个仓库之后应该先做什么? 1、下载仓库,创建上游代码库,查看当前的分支情况 git clone https://github.com/<your_name>/<repo_name>.git git remote add upstream git…...
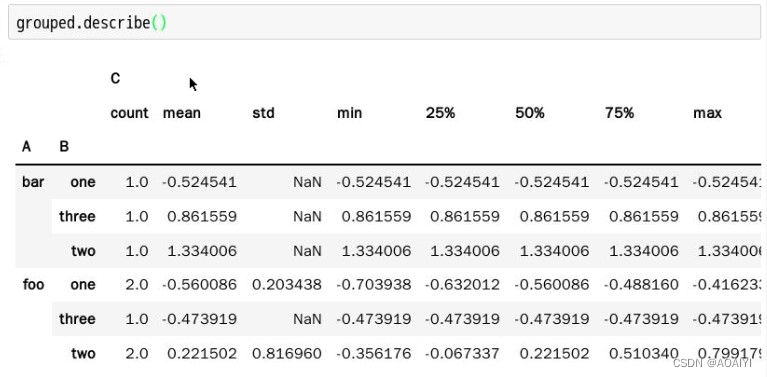
pandas——groupby操作
Pandas——groupby操作 文章目录Pandas——groupby操作一、实验目的二、实验原理三、实验环境四、实验内容五、实验步骤一、实验目的 熟练掌握pandas中的groupby操作 二、实验原理 groupby(byNone, axis0, levelNone, as_indexTrue, sortTrue, group_keysTrue, squeezeFalse&…...
webpack.config.js哪里找?react项目关闭eslint监测
目录 webpack.config.js哪里找? react项目关闭eslint监测 webpack.config.js哪里找? 在React项目中,当我们需要修改一些配置时,发现找不到webpack.config.js,是我们创建的项目有问题吗,还需新创建项目的项…...
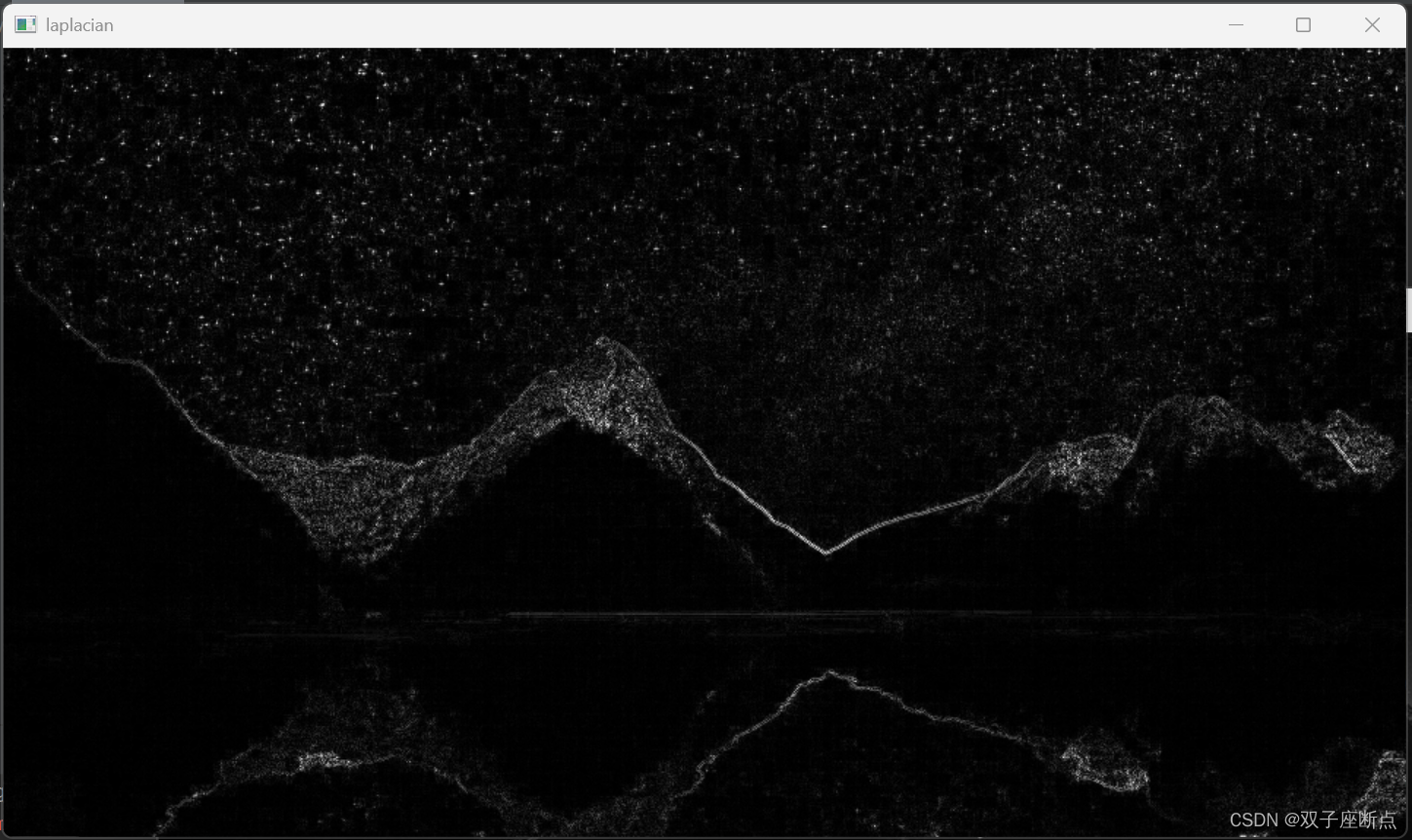
OpenCV 图像梯度算子
本文是OpenCV图像视觉入门之路的第12篇文章,本文详细的介绍了图像梯度算子的各种操作,例如:Sobel算子Scharr算子laplacian算子等操作。 OpenCV 图像梯度算子目录 1 Sobel算子 2 Scharr算子 3 laplacian算子 1 Sobel算子 Sobel算子是一种图…...
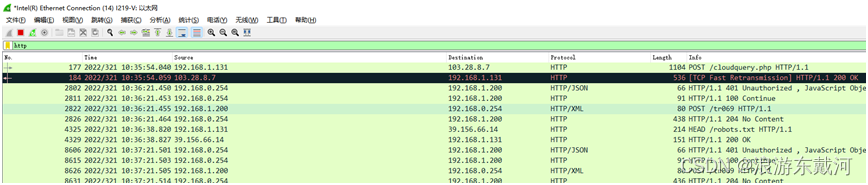
Linux c编程之Wireshark
Wireshark是一个网络报文分析软件,是网络应用问题分析必不可少的工具软件。网络管理员可以使用wireshark排查网络问题。程序开发人员可以用来分析应用协议、定位分析应用问题。无论是网络应用程序开发人员、测试人员、部署人员、技术支持人员,掌握wireshark的使用对于分析网络…...

极客时间_FlinkSQL 实战
一、批处理以及流处理技术发展 1.Lambda架构三层划分Batch Layer、Speed Layer和Serving Layer。 ①、Batch Layer:主要用于实现对历史数据计算结果的保存,每天计算的结果都保存成为一个Batch View,然后通过对Batch View的计算,实现历史数据的计算。 ②、Speed Layer正是用…...
Pytorch 混合精度训练 (Automatically Mixed Precision, AMP)
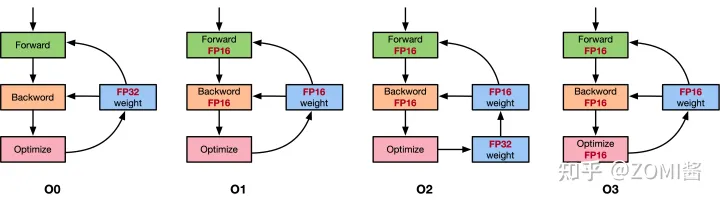
Contents混合精度训练 (Mixed Precision Training)单精度浮点数 (FP32) 和半精度浮点数 (FP16)为什么要用 FP16为什么只用 FP16 会有问题解决方案损失缩放 (Loss Scaling)FP32 权重备份黑名单Tensor CoreNVIDIA apex 库代码解读opt-level (o1, o2, o3, o4)apex 的 o1 实现apex …...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
