二叉树OJ题(上)
✅每日一练:100. 相同的树 - 力扣(LeetCode)
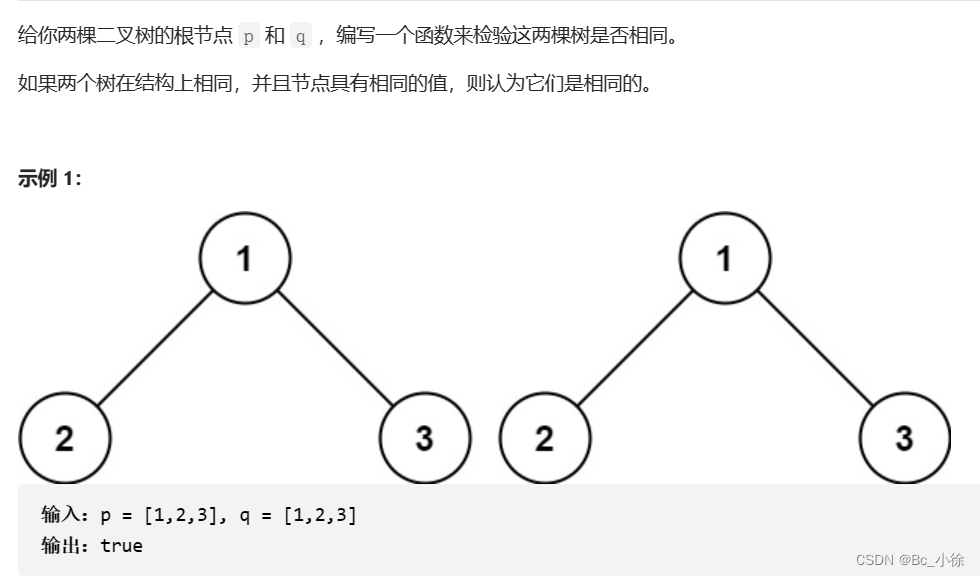
题目的意思是俩棵树的结构不仅要相同,而且每个节点的值还要相同,如果满足上面2个条件,则成立!
解题思路:
从三个方面去考虑:
1.如果p,q都为空,那么一定相同;
2.如果p为空,q不为空,或者p不为空,q为空,那么一定不相同;
3.如果二者都不为空,那么需要判断根节点,如果根节点不相同,那么一定不相同,如果相同,我们需要比较左右子树的值和左右子树的结构;
代码:
public boolean isSameTree(TreeNode p, TreeNode q) {//如果p,q都为空,那么这2个树一定相同if (p == null && q == null) {return true;}//如果q为空,p不为空,那么一定不相同,或者p为空,q不为空,那么一定不相同if (p != null && q == null||p == null && q != null) {return false;}//如果p,q都不为空,那么要判断值,如果值不相同,那么一定不相同if (p.val != q.val) {return false;}//如果p,q都不为空,并且p,q的值相同,那么要判断p,q的左右子树的值,如果相同为真,反之;return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}✅每日一练:572. 另一棵树的子树 - 力扣(LeetCode)
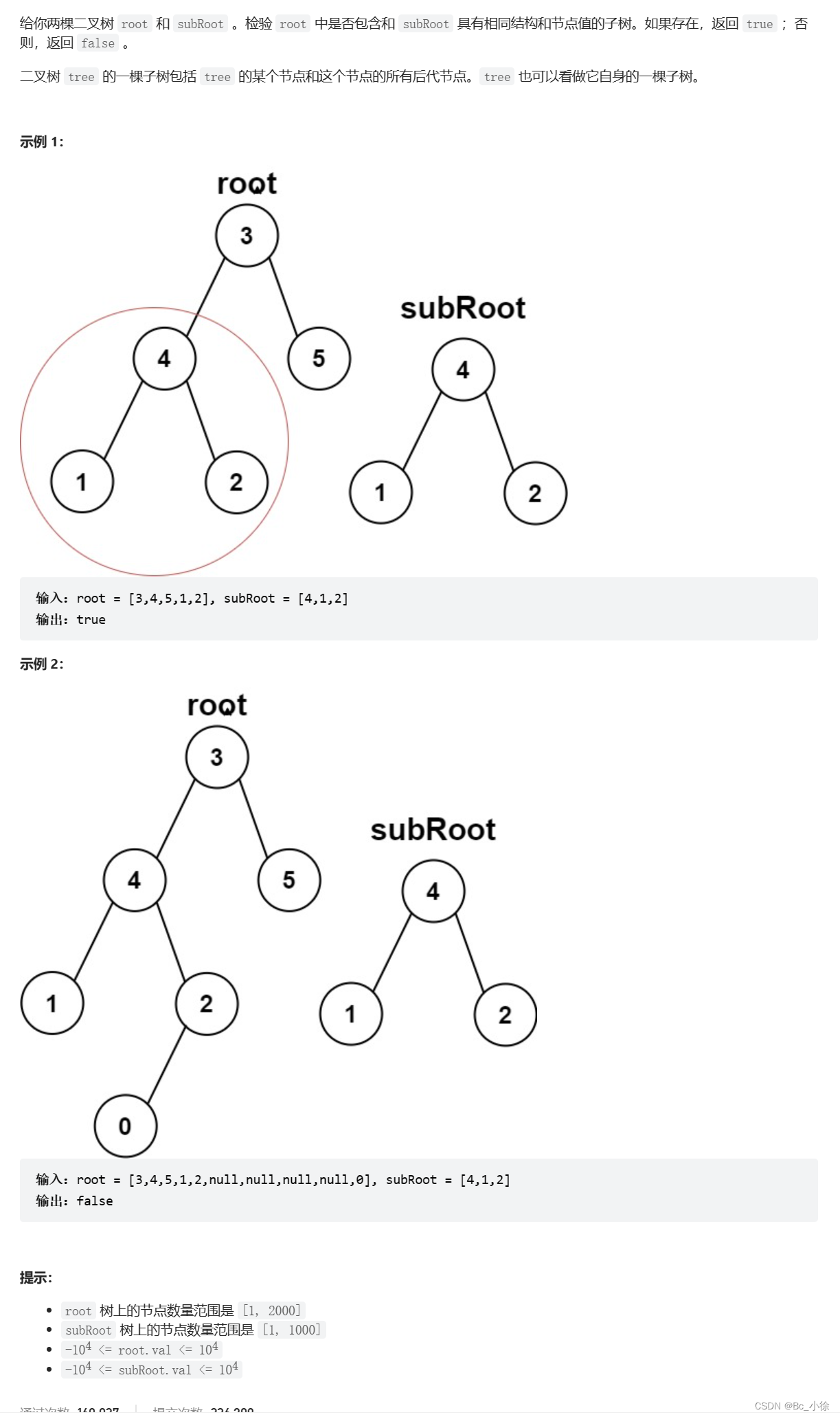
解题思路:
1.如果根节点为空,那么返回false;
2.如果根节点相同,那么我们需要判断这2棵树是否相同,我们可以借助上面写的isSameTree方法去判断,如果相同,则subRoot是root的子树;
3.如果根节点不相同,我们需要在左子树或者右子树去找是否有和subRoot相同的树;
代码:
public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(root == null||subRoot == null){return false;}//判断2棵树是否相同if(isSameTree(root,subRoot)){return true;}//判断左子树是否有subRootif(isSubtree(root.left,subRoot)){return true;}//判断右子树是否有subRootif(isSubtree(root.right,subRoot)){return true;}return false;}public boolean isSameTree(TreeNode p, TreeNode q) {//如果p,q都为空,那么这2个树一定相同if (p == null && q == null) {return true;}//如果q为空,p不为空,那么一定不相同if (p != null && q == null) {return false;}//如果p为空,q不为空,那么一定不相同if (p == null && q != null) {return false;}//如果p,q都不为空,那么要判断值,如果值不相同,那么一定不相同if (p.val != q.val) {return false;}//如果p,q都不为空,并且p,q的值相同,那么要判断p,q的左右子树的值,如果相同为真,反之;return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}✅每日一练:226. 翻转二叉树 - 力扣(LeetCode)
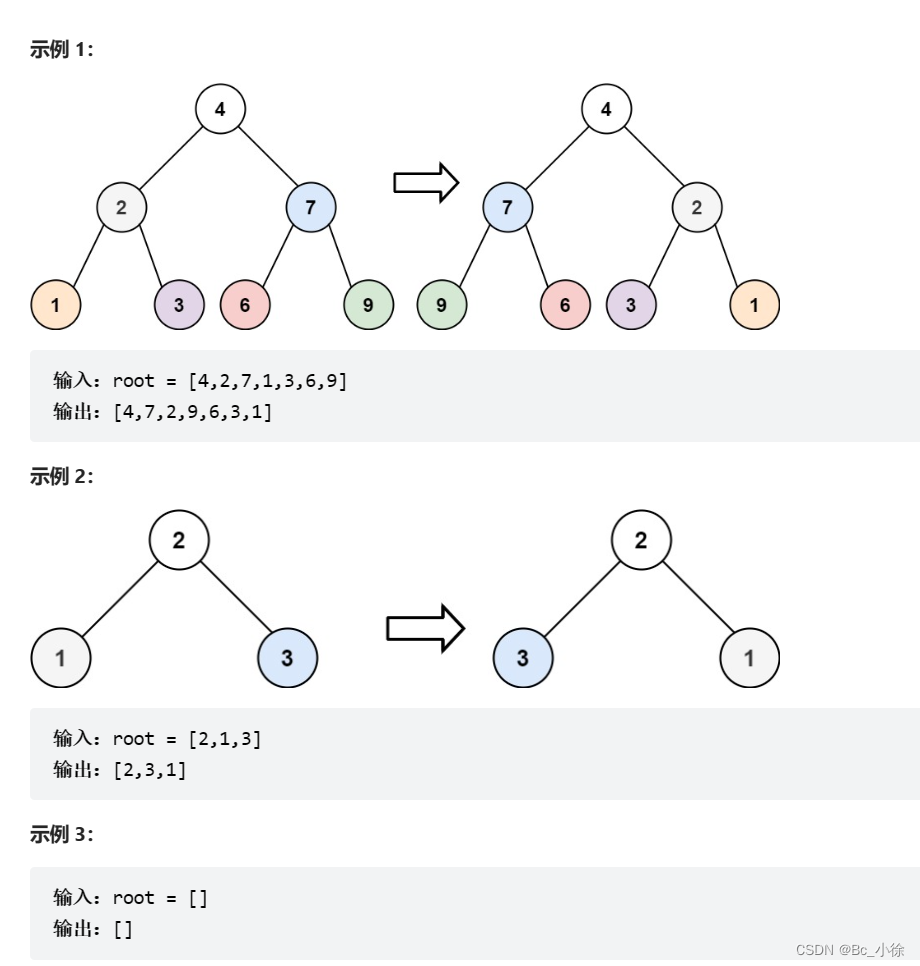
解题思路:
利用递归思想,如果根节点不为空,递归左右子树的值进行交换;
public TreeNode invertTree(TreeNode root) {if (root == null) {return null;}TreeNode tmp = root.left;root.left = root.right;root.right = tmp;invertTree(root.left);invertTree(root.right);return root;}✅每日一练:110. 平衡二叉树 - 力扣(LeetCode)
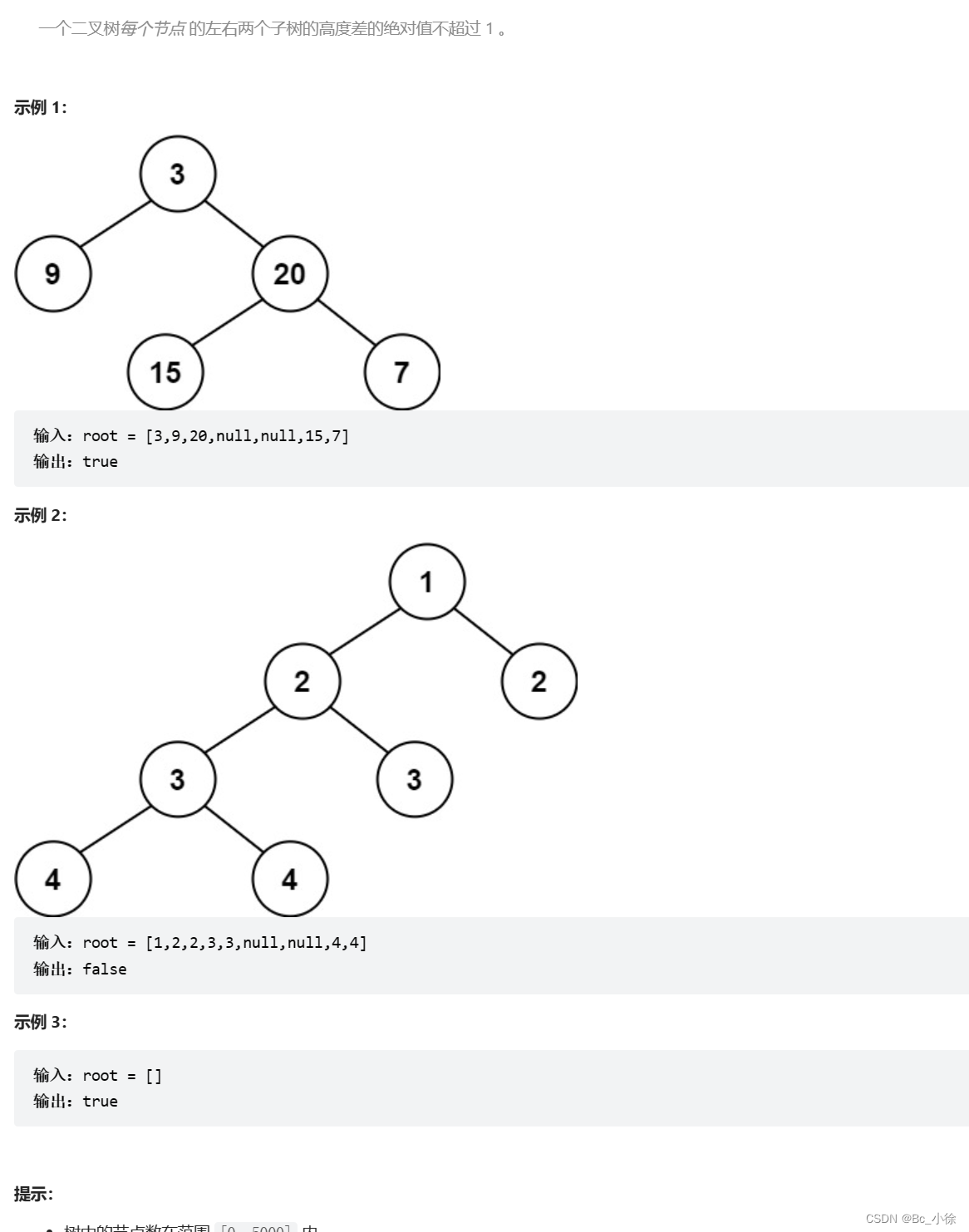
解题思路:
题目的意思就是每个节点的左右子树的高度差的绝对值不能超过1,就是平衡二叉树,则满足题目需求;
代码:
public boolean isBalanced(TreeNode root) {if(root == null){return true;}int leftH = getHeight(root.left);int rightH =getHeight(root.right);return Math.abs(leftH-rightH)<=1 && isBalanced(root.left) && isBalanced(root.right);}public int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}✅每日一练:101. 对称二叉树 - 力扣(LeetCode)
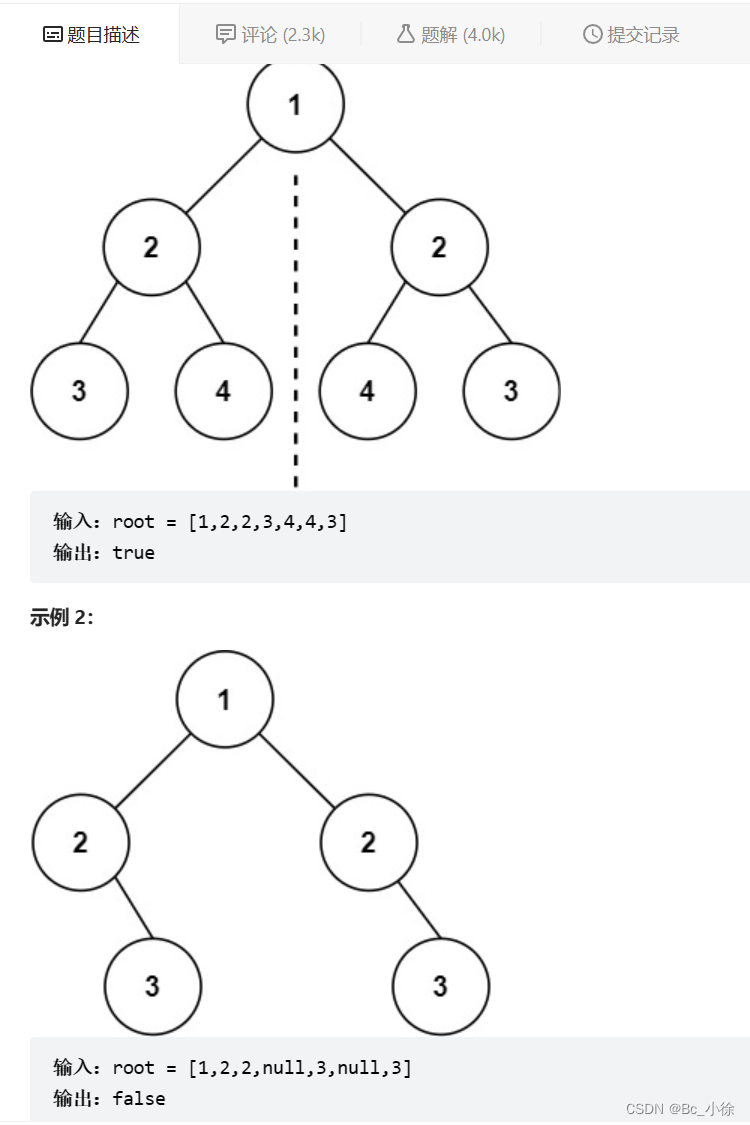
解题思路:
1.如果根节点为空,那么对称;
2.如果根节点不为空,根节点的左子树为空,根节点的右子树不为空,或者根节点的左子树不为空,根节点的右子树为空,那么一定不对称;
3.如果根节点的左子树的值和右子树的值不相等,那么一定不对称;
4.如果上面条件都没有满足到,那么我们需要判断左子树的左子树是否和右子树的右子树相等,左子树的右子树是否和右子树的左子树相等,如果相等,则对称;
代码:
public boolean isSymmetric(TreeNode root) {if (root == null) {return true;}return isSymmetricChild(root.left, root.right);}public boolean isSymmetricChild(TreeNode leftTree, TreeNode rightTree) {if (leftTree == null && rightTree == null) {return true;}if (leftTree != null && rightTree == null || leftTree == null && rightTree != null) {return false;}if (leftTree.val != rightTree.val) {return false;}return isSymmetricChild(leftTree.left, rightTree.right) && isSymmetricChild(leftTree.right, rightTree.left);}✅每日一练:102. 二叉树的层序遍历 - 力扣(LeetCode)
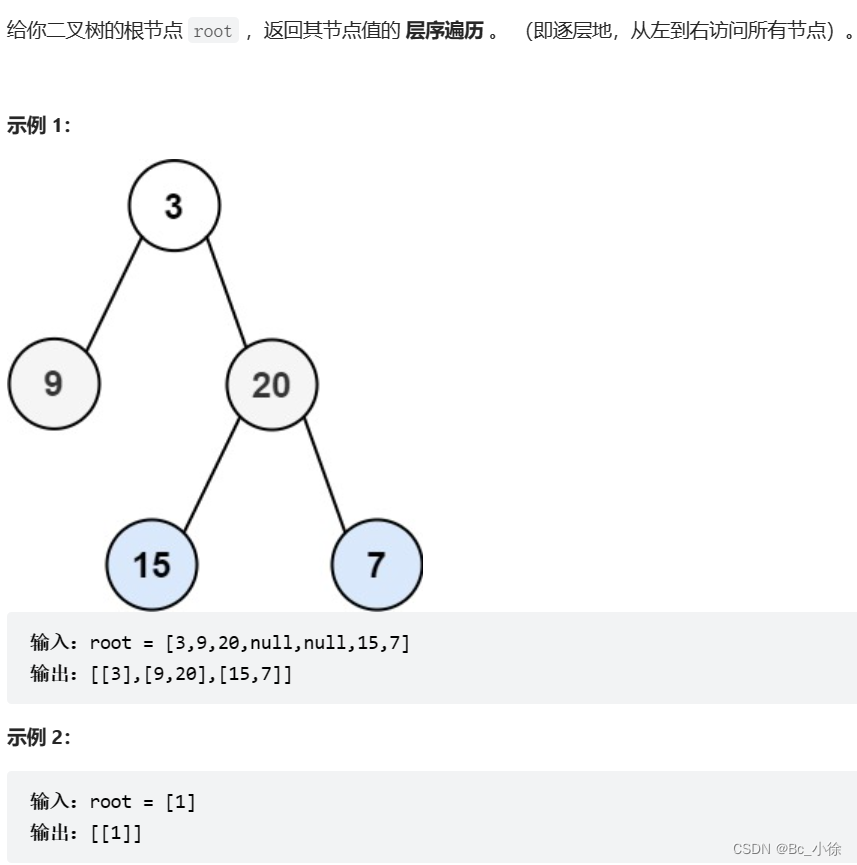
解题思路:
层序遍历就是从上到下,从左到右逐个遍历,层序遍历相对于其他遍历简单,但是代码实现起来没有那么简单 ,我们可以利用队列去实现他,利用队列先进先出的特点去实现:
首先判断根节点,如果为空就返回,如果不为空,就把根节点放进队列,用while循环来判断当前队列是否为空,再定义一个变量来存放根节点的值,然后打印,打印完再去判断根节点的左右子树,如果不为空,就入队,依次执行下去我们可以得到层序遍历,代码:
public void levelOrder1(TreeNode root) {if (root == null) {return;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode cur = queue.poll();System.out.print(cur.val + " ");if (cur.left != null) {queue.offer(cur.left);}if (cur.right != null) {queue.offer(cur.right);}}}这是没有返回值的方法,但是这道oj题的返回值是List<List<Integer>>,所以这是我们就要换种思路来写这题了,大致的思路就是,我们需要2的循环,用当前队列是否为空作为第一个循环条件,当前队列里面元素的个数的大小作为子循环条件,代码:
public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();if (root == null) {return list;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {int size = queue.size();//用来判断当前队列的大小//System.out.print(cur.val);List<Integer> tmp = new ArrayList<>();while (size != 0) {TreeNode cur = queue.poll();tmp.add(cur.val);size--;if (cur.left != null) {queue.offer(cur.left);}if (cur.right != null) {queue.offer(cur.right);}}list.add(tmp);//将每层的结果放到list中}return list;}相关文章:

二叉树OJ题(上)
✅每日一练:100. 相同的树 - 力扣(LeetCode) 题目的意思是俩棵树的结构不仅要相同,而且每个节点的值还要相同,如果满足上面2个条件,则成立! 解题思路: 从三个方面去考虑࿱…...

第一章 PDF语法
第一章 PDF语法PDF ObjectsNull ObjectsBoolean ObjectsNumeric ObjectsName ObjectsString ObjectsArray ObjectsDictionary ObjectsName treesNumber treesStream ObjectsDirect versus Indirect ObjectsFile StructureWhite-SpaceThe Four Sections of a PDFHeaderTrailerBo…...
IntelliJ IDEA 创建JavaFX项目运行
IntelliJ IDEA 创建JavaFX项目运行JavaFX官网文档:https://openjfx.io/openjfx-docs/ JavaFX 2008年12月05日诞生,是一个开源的下一代客户端应用程序平台,适用于基于 Java 构建的桌面、移动和嵌入式系统。这是许多个人和公司的协作努力&#…...

IC封装常见形式
参考:https://blog.csdn.net/dhs888888/article/details/127673300?utm_mediumdistribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-127673300-blog-115610343.pc_relevant_multi_platform_whitelistv4&spm1001.2101.3001.4242…...

Linux通配符、转义符讲解
目录 通配符 通过通配符定义匹配条件 转义符 将所有的逻辑操作符都转换成字符 通配符 通过通配符定义匹配条件 * 任意字符都可以通配(也可以匹配空值) ? 匹配单个字符 [a-z] 匹配单个的小写英文字母 [A-Z] 匹配单个的大写英文…...

[OpenMMLab]提交pr时所需的git操作
git开发流程 准备工作 作为一个开发者,fork一个仓库之后应该先做什么? 1、下载仓库,创建上游代码库,查看当前的分支情况 git clone https://github.com/<your_name>/<repo_name>.git git remote add upstream git…...
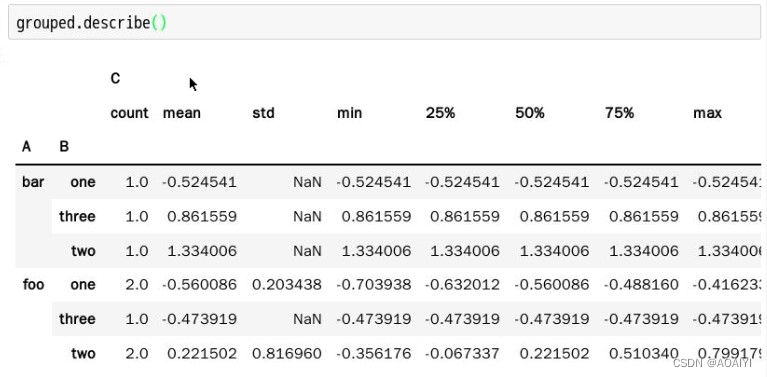
pandas——groupby操作
Pandas——groupby操作 文章目录Pandas——groupby操作一、实验目的二、实验原理三、实验环境四、实验内容五、实验步骤一、实验目的 熟练掌握pandas中的groupby操作 二、实验原理 groupby(byNone, axis0, levelNone, as_indexTrue, sortTrue, group_keysTrue, squeezeFalse&…...
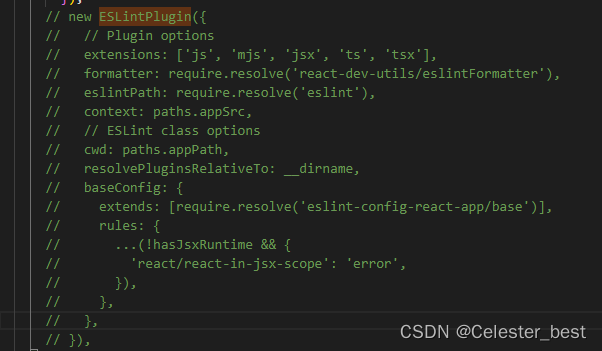
webpack.config.js哪里找?react项目关闭eslint监测
目录 webpack.config.js哪里找? react项目关闭eslint监测 webpack.config.js哪里找? 在React项目中,当我们需要修改一些配置时,发现找不到webpack.config.js,是我们创建的项目有问题吗,还需新创建项目的项…...
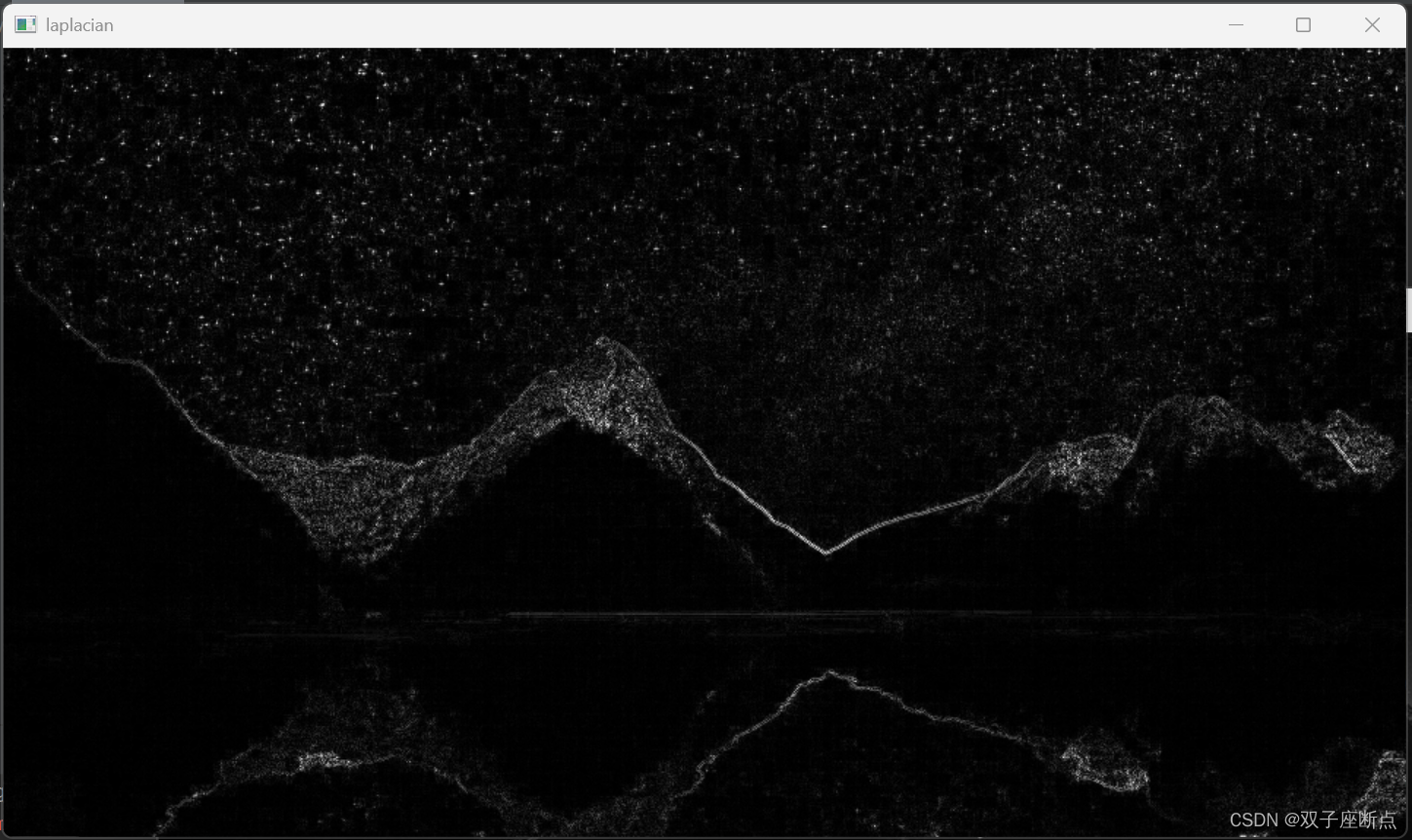
OpenCV 图像梯度算子
本文是OpenCV图像视觉入门之路的第12篇文章,本文详细的介绍了图像梯度算子的各种操作,例如:Sobel算子Scharr算子laplacian算子等操作。 OpenCV 图像梯度算子目录 1 Sobel算子 2 Scharr算子 3 laplacian算子 1 Sobel算子 Sobel算子是一种图…...
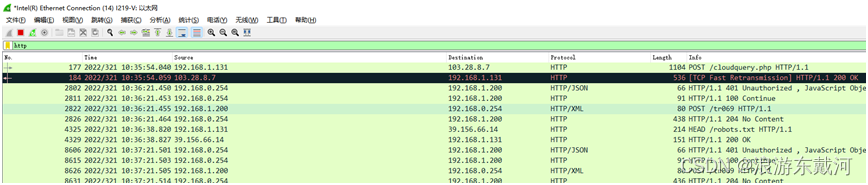
Linux c编程之Wireshark
Wireshark是一个网络报文分析软件,是网络应用问题分析必不可少的工具软件。网络管理员可以使用wireshark排查网络问题。程序开发人员可以用来分析应用协议、定位分析应用问题。无论是网络应用程序开发人员、测试人员、部署人员、技术支持人员,掌握wireshark的使用对于分析网络…...

极客时间_FlinkSQL 实战
一、批处理以及流处理技术发展 1.Lambda架构三层划分Batch Layer、Speed Layer和Serving Layer。 ①、Batch Layer:主要用于实现对历史数据计算结果的保存,每天计算的结果都保存成为一个Batch View,然后通过对Batch View的计算,实现历史数据的计算。 ②、Speed Layer正是用…...
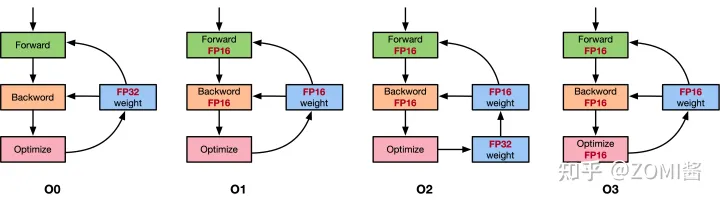
Pytorch 混合精度训练 (Automatically Mixed Precision, AMP)
Contents混合精度训练 (Mixed Precision Training)单精度浮点数 (FP32) 和半精度浮点数 (FP16)为什么要用 FP16为什么只用 FP16 会有问题解决方案损失缩放 (Loss Scaling)FP32 权重备份黑名单Tensor CoreNVIDIA apex 库代码解读opt-level (o1, o2, o3, o4)apex 的 o1 实现apex …...

使用太极taichi写一个只有一个三角形的有限元
公式来源 https://blog.csdn.net/weixin_43940314/article/details/128935230 GAME103 https://games-cn.org/games103-slides/ 初始化我们的三角形 全局的坐标范围为0-1 我们的三角形如图所示 ti.kernel def init():X[0] [0.5, 0.5]X[1] [0.5, 0.6]X[2] [0.6, 0.5]x[0…...
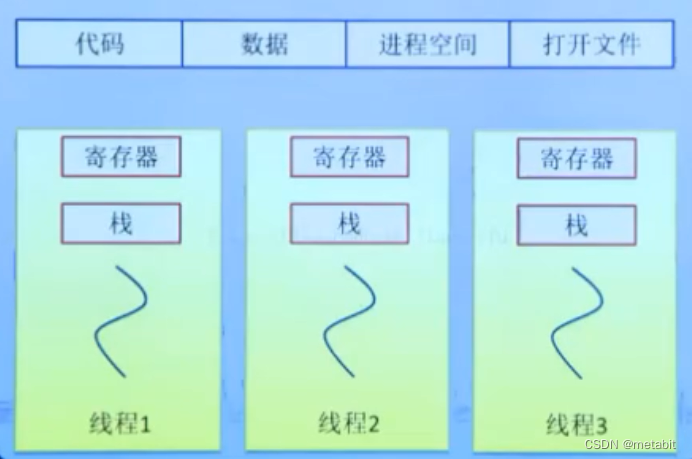
进程,线程
进程是操作系统分配资源的基本单位,线程是CPU调度的基本单位。 PCB:进程控制块,操作系统描述程序的运行状态,通过结构体task,struct{…},统称为PCB(process control block)。是进程管理和控制的…...

第03章_基本的SELECT语句
第03章_基本的SELECT语句 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 1. SQL概述 1.1 SQL背景知识 1946 年,世界上第一台电脑诞生,如今,借由这台电脑发展…...

干货 | 简单了解运算放大器...
运算放大器发明至今已有数十年的历史,从最早的真空管演变为如今的集成电路,它在不同的电子产品中一直发挥着举足轻重的作用。而现如今信息家电、手机、PDA、网络等新兴应用的兴起更是将运算放大器推向了一个新的高度。01 运算放大器简述运算放大器&#…...
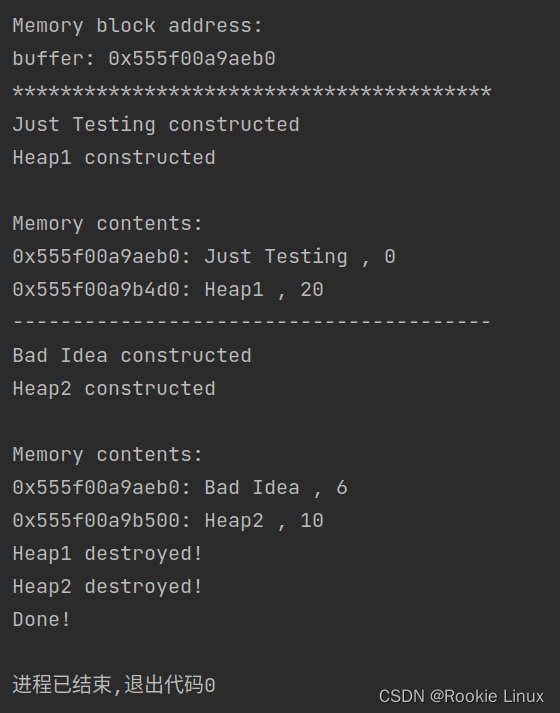
C++定位new用法及注意事项
使用定位new创建对象,显式调用析构函数是必须的,这是析构函数必须被显式调用的少数情形之一!, 另有一点!!!析构函数的调用必须与对象的构造顺序相反!切记!!&a…...

【Android笔记75】Android之翻页标签栏PagerTabStrip组件介绍及其使用
这篇文章,主要介绍Android之翻页标签栏PagerTabStrip组件及其使用。 目录 一、PagerTabStrip翻页标签栏 1.1、PagerTabStrip介绍 1.2、PagerTabStrip的使用 (1)创建布局文件...

【Kafka】【二】消息队列的流派
消息队列的流派 ⽬前消息队列的中间件选型有很多种: rabbitMQ:内部的可玩性(功能性)是⾮常强的rocketMQ: 阿⾥内部⼀个⼤神,根据kafka的内部执⾏原理,⼿写的⼀个消息队列中间 件。性能是与Kaf…...

现代 cmake (cmake 3.x) 操作大全
cmake 是一个跨平台编译工具,它面向各种平台提供适配的编译系统配置文件,进而调用这些编译系统完成编译工作。cmake 进入3.x 版本,指令大量更新,一些老的指令开始被新的指令集替代,并加入了一些更加高效的指令/参数。本…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
