Golang编译-如何忽略某些文件去编译
在 Go 语言中,编译好的二进制文件不会被再次加入到编译过程中。Go 编译器只会编译源代码文件(如 .go 文件),而不会将已经编译好的二进制文件(如可执行文件或静态库)作为输入来进行编译。
详细解释:
-
编译流程:
- Go 编译器从指定的源代码文件(
.go文件)中读取代码,并生成中间代码,然后生成最终的二进制可执行文件。 - 生成的二进制文件是最终的产物,不会作为输入再次被编译。
- Go 编译器从指定的源代码文件(
-
生成的二进制文件:
- 当你运行
go build命令时,Go 会生成一个二进制文件(在 Unix-like 系统上通常没有扩展名,在 Windows 上是.exe文件)。 - 这个二进制文件是完整的可执行文件,包含所有需要的代码和依赖项。它是独立的产物,已经与编译过程无关。
- 当你运行
-
防止意外编译:
- 如果你不小心将编译生成的二进制文件保存在源代码目录下,Go 编译器会自动忽略它们,因为它只会寻找源代码文件来编译。
- 例如,如果你在项目根目录下运行
go build,编译生成的可执行文件不会干扰未来的编译过程。
示例:
假设你有以下目录结构:
plaintext
复制代码
project/ ├── main.go ├── utils.go ├── main # 编译生成的二进制文件 └── some_other.go
在这个结构中,main 是通过编译生成的二进制文件。再次运行 go build 时,Go 编译器会:
- 只读取
main.go、utils.go和some_other.go文件进行编译。 - 忽略
main二进制文件。
总结
- Go 编译器不会将编译好的二进制文件作为编译过程的输入。
- 编译时只会考虑源代码文件(
.go文件)。 - 生成的二进制文件与后续的编译过程无关,且不会影响编译。
这意味着在项目中,生成的二进制文件可以安全地留在目录中,而不会意外被再次编译。
4o
相关文章:

Golang编译-如何忽略某些文件去编译
在 Go 语言中,编译好的二进制文件不会被再次加入到编译过程中。Go 编译器只会编译源代码文件(如 .go 文件),而不会将已经编译好的二进制文件(如可执行文件或静态库)作为输入来进行编译。 详细解释…...
有哪些适合中型企业的人力资源管理系统推荐?
本文主要介绍了以下几款人力资源管理系统:Moka、OrangeHRM、Verint、希沃人事、UKG Pro、大易Dayee、DingTalk、致远OA、卓望ShineHR、GoCo。 在选择人力资源管理系统时,中型企业面临着诸多挑战:如何确保系统既能满足现有需求,又能…...

活动回顾|首次 Cloudberry Database Meetup · 北京站成功举办
8 月 3 日,由酷克数据 HashData 主办的 Cloudberry Database Meetup 北京站活动圆满结束。本次 Meetup 以“以开源应对 Greenplum 闭源,原厂开发者再聚首”为主题,深入探讨了 Greenplum 闭源所带来的影响,并聚焦于 Cloudberry Dat…...

C语言 软件设计的七大原则,及其应用案例
1. 单一职责原则 (Single Responsibility Principle, SRP) 定义: 一个模块或函数应当只有一个引起变化的原因。 应用案例: 在嵌入式系统中,可以将传感器数据的读取和处理分开成不同的函数。例如: // 读取传感器数据的函数 floa…...

初学嵌入式-C语言常犯错误详解
1、对于下面这道题,估计有很多人会选择B答案,但其实答案是D 2.int a10, b9,c9,d; d b || (a>c),请问上述代码执行完毕后a b c d的值分别是 。 A、10 9 10 9 B、10 10 10 1 C、10 9 10 1 D、10 10 9 1 答案解释: 在C语言…...
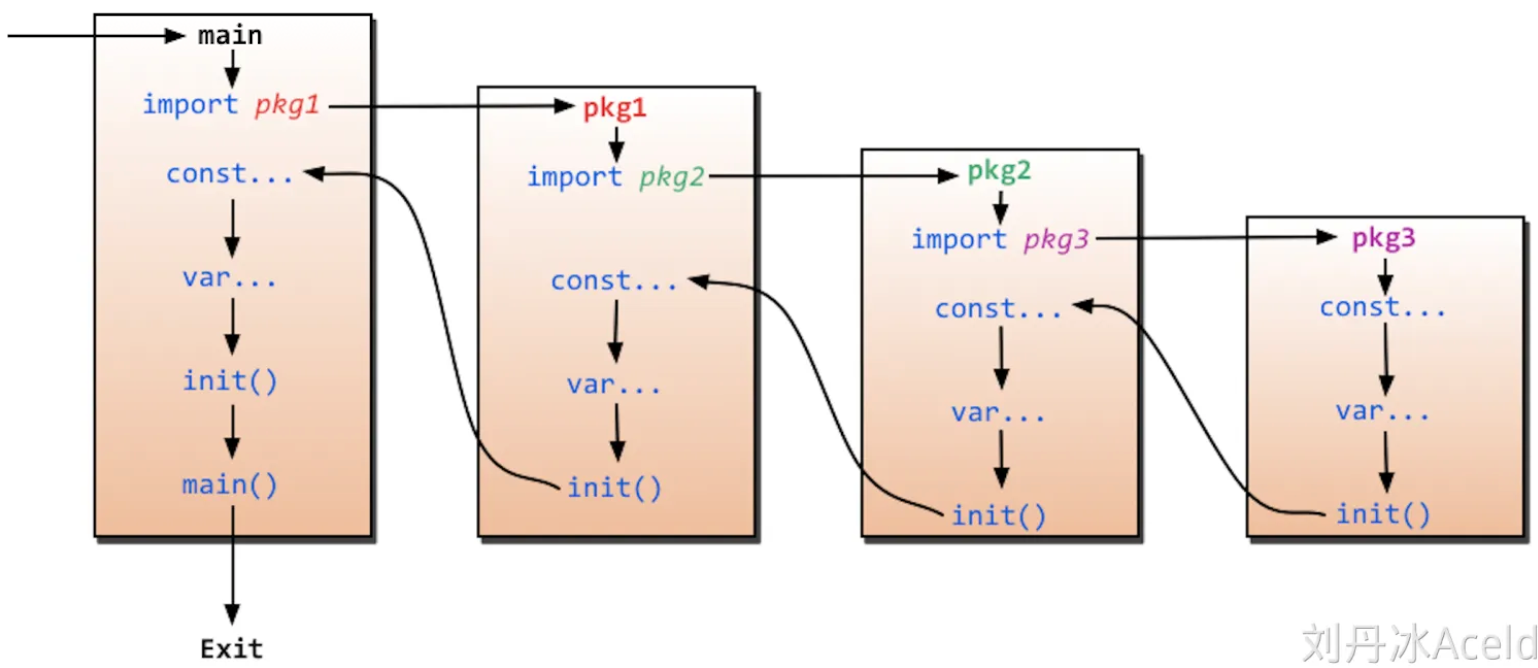
Golang 语法入门
Golang 语法入门 Hello World package mainimport "fmt"func main() {fmt.Println("hello world") }变量 package mainimport "fmt"// 全局变量 var ans 123 var cnt intfunc main() {// 单个局部变量a : 114514// 多个局部变量b, c : 114, …...

Filebeat+Kafka+ELK
架构: 部署: #配置nginx,部署filebeat systemctl stop firewalld setenforce 0 systemctl restart nginx#解压filebeat tar -xf filebeat-6.7.2-linux-x86_64.tar.gz mv filebeat-6.7.2-linux-x86_64 filebeat#日志收集 cd firebeat vim fil…...

Python 为Excel单元格设置填充\背景色 (纯色、渐变、图案)
在使用Excel进行数据处理和分析时,对特定单元格进行背景颜色填充不仅能够提升工作表的视觉吸引力,还能帮助用户快速识别和区分不同类别的数据,增强数据的可读性和理解性。 本文将通过以下三个示例详细介绍如何使用Python在Excel中设置不同的单…...

家里浮毛粉尘到处飞?宠物空气净化器出动帮你解决
由于家里收养的十几只流浪猫咪夏季掉毛非常严重,整个房子弥漫着猫毛,而且这十几只里面有七八只还是长毛的品种,掉落的毛发都因为太长而直接掉落成毛团,而短毛的那几只也在掉毛,这十几只掉下的浮毛,家里已经…...

计算机网络ISO七层网络模型及TCP
思维导图(通俗理解) 首先,先用最通俗的话来描述ISO七层模型,思维导图结构如下: ISO七层网络模型概念 应用层(Application Layer):应用层是OSI模型的最高层,直接与用户交…...

机器学习知识点全面总结
一、机器学习基础概念 1、什么是机器学习 机器学习是一种人工智能技术,通过对数据的学习和分析,让计算机系统自动提高其性能。简而言之,机器学习是一种从数据中学习规律和模式的方法,通过数据来预测、分类或者决策。 机器学习的本…...

【研发日记】嵌入式处理器技能解锁(三)——TI C2000 DSP的C28x内核
文章目录 前言 背景介绍 C28x内核 浮点单元(FPU) 快速整数除法单元(FINTDIV) 三角数学单元(TMU) VCRC单元 CPU总线 指令流水线 总结 参考资料 前言 见《【研发日记】嵌入式处理器技能解锁(一)——多任务异步执行调度的三种方法》 见《【研发日记】嵌入式处理器技能解…...

LeetCode.27.移除元素
题目描述: 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。 假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以…...
可重入锁总结)
redis面试(十二)可重入锁总结
可重入锁总结 从实现原理以及源码的层面,真正剖析和了解到了redis分布式锁的企业级的实现,这个分布式锁实现的还是非常漂亮的,麻雀虽小,五脏俱全,分布式的可重入锁,总结一下流程 (1࿰…...

软件测试知识点3
063、一份测试计划应该包括哪些内容? 背景、项目简介、目的、测试范围、测试策略、人员分工、资源要求、进度计划、参考文档、常用术语、提交文档、风险分析。 065、如何定位测试用例的作用? 组织性:编写、组织性、功能覆盖、重复性、跟踪、测试确认 066、什么…...

WPF Treeview开启虚拟化后如何找到TreeViewItem
用VirtualizingStackPanel的BringIndexIntoViewPublic方法就好,没必要像微软给的例子那样还要继承一个VirtualizingStackPanel /// <summary> /// Recursively search for an item in this subtree. /// </summary> /// <param name"container…...

给python初学者的一些建议
写在开篇 关于Python,可以这么说,这几年借着数据科学、机器学习与人工智能的东风,Python 老树开新花,在风口浪尖上居高不下。 Python 之所以这么受大家的青睐,是因为它语言简洁,上手容易,让非…...

【Python学习手册(第四版)】学习笔记17-作用域
个人总结难免疏漏,请多包涵。更多内容请查看原文。本文以及学习笔记系列仅用于个人学习、研究交流。 本文介绍Python作用域,介绍了变量名解析的LEGB原则,以及内置作用域,全局作用域global语句,嵌套作用域及nonlocal语…...

大语言模型(LLM)文本预处理实战
大语言模型(LLM)文本预处理实战 文章目录 大语言模型(LLM)文本预处理实战2.1 理解词嵌入2.2 文本分词2.3 将 token 转换为 token ID2.4 添加特殊上下文 token2.5 字节对编码 (BytePair Encoding, BPE)2.6 使用滑动窗口进行数据采样…...

宠物健康新守护:智能听诊器的家庭应用
宠物已成为我们情感的寄托和生活的一部分,为宠物的健康守护带来了科技的温度。 科技与关怀结合 这款智能听诊器,以其科技感和关怀精神,为宠物的健康监测提供了全新的视角。 家庭友好设计:考虑到家庭使用环境,智能听…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
