【红黑树】
红黑树
小杨
红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。

红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点 。----->每条路径黑色节点数量相等。
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
实际的红黑树,最长和最短并不一定存在。红黑树最短路径:h(全黑),最长路径:2*h(一黑一红).
最短路径*2>=最长路径
就查找而言,最短路径:logN,最长路径:2*logN.
红黑树节点定义
//枚举定义结点的颜色
enum Colour
{RED,BLACK
};//红黑树结点的定义
template<class K, class V>
struct RBTreeNode
{//三叉链RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;//存储的键值对pair<K, V> _kv;//结点的颜色int _col; //红/黑//构造函数RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};
红黑树结构
为了后续实现关联式容器简单,红黑树的实现中增加一个头结点,因为跟节点必须为黑色,为了与根节点进行区分,将头结点给成黑色,并且让头结点的 pParent 域指向红黑树的根节点,pLeft域指向红黑树中最小的节点,_pRight域指向红黑树中最大的节点,如下:

红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
- 按照二叉搜索的树规则插入新节点
- 检测新节点插入后,红黑树的性质是否造到破坏
我们默认新节点默认颜色为红色(主动破坏红黑树的性质3),如果新节点默认是黑色(那就相当于破换了性质4),破坏性质3比较好控制一点.
分析种数情况:以下图这棵树为例子:

如果cur不是新增节点:若cde具有每条路径都只有一个黑色节点,那就是有3种情况.

因此cde的组合情况有333=27种。
cur只能为x的情况,此时新增的红色节点有4种插入情况(新增节点一定是在a、b
的下面)。样例为下图:

如果cde具有2个黑色节点?估计得上万。
接下来看红黑树性质遭到破坏如何调整?
注意:我们看到的树,可能是一棵完整的树,也可能是一棵子树。
情况一:cur为红,p为红,g为黑,u存在且为红
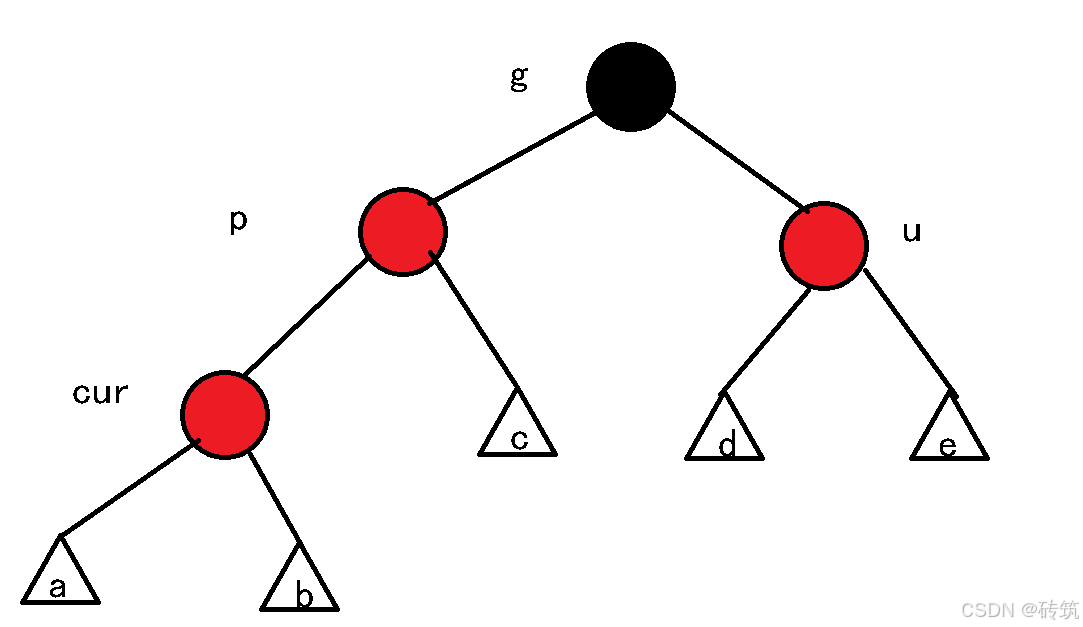
此时cur为新增,如果如果p为黑,那么就结束了,若p也为红,那么就需要调整了,红黑树其实就是先尽量调整颜色,实在不行的话就进行旋转。但是调整颜色的话主要看的是u,而根据u可以分成两种情况。1.u存在且为红;2.u不存在或者u存在且为黑。
调整后如下图:

如果g是根节点,调整完成后,需要将g改成黑色。
如果g是子树,g一定有双亲,且g的双亲如果是红色,需要继续向上调整。
对为什么要继续进行向上调整的解释:

情况二:cur为红,p为红,g为黑,u不存在/u存在且为黑

说明:u的情况有两种
- 如果u节点不存在,则cur一定是新插入节点,因为如果cur不是新插入节点,则cur和p一定有一个节点的颜色是黑色,就不满足红黑树性质4:每条路径黑色节点个数相同。
- 如果u节点存在,则其一定是黑色的,那么cur节点原来的颜色一定是黑色的,现在看到上图左其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色有黑色改成红色。
p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色–p变黑,g变红
情况三:cur为红,p为红,g为黑,u不存在/u存在且为黑

p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,
p为g的右孩子,cur为p的左孩子,则针对p做右单旋转
则转换成了情况2
红黑树的验证
红黑树的检测分为两步:
- 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 检测其是否满足红黑树的性质
bool IsValidRBTree()
{PNode pRoot = GetRoot();// 空树也是红黑树if (nullptr == pRoot)return true;// 检测根节点是否满足情况if (BLACK != pRoot->_color){cout << "违反红黑树性质二:根节点必须为黑色" << endl;return false;}// 获取任意一条路径中黑色节点的个数size_t blackCount = 0;PNode pCur = pRoot;while (pCur){if (BLACK == pCur->_color)blackCount++;pCur = pCur->_pLeft;}// 检测是否满足红黑树的性质,k用来记录路径中黑色节点的个数size_t k = 0;return _IsValidRBTree(pRoot, k, blackCount);
}
bool _IsValidRBTree(PNode pRoot, size_t k, const size_t blackCount)
{//走到null之后,判断k和black是否相等if (nullptr == pRoot){if (k != blackCount){cout << "违反性质四:每条路径中黑色节点的个数必须相同" << endl;return false;}return true;}// 统计黑色节点的个数if (BLACK == pRoot->_color)k++;// 检测当前节点与其双亲是否都为红色PNode pParent = pRoot->_pParent;if (pParent && RED == pParent->_color && RED == pRoot->_color){cout << "违反性质三:没有连在一起的红色节点" << endl;return false;}return _IsValidRBTree(pRoot->_pLeft, k, blackCount) &&_IsValidRBTree(pRoot->_pRight, k, blackCount);
}
红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(logN),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
红黑树的应用
- C++ STL库 – map/set、mutil_map/mutil_set
- Java 库
- linux内核
- 其他一些库
红黑树实现代码:
//枚举定义结点的颜色
enum Colour
{RED,BLACK
};//红黑树结点的定义
template<class K, class V>
struct RBTreeNode
{//三叉链RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;//存储的键值对pair<K, V> _kv;//结点的颜色int _col; //红/黑//构造函数RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};//红黑树的实现
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public://构造函数RBTree():_root(nullptr){}//拷贝构造RBTree(const RBTree<K, V>& t){_root = _Copy(t._root, nullptr);}//赋值运算符重载(现代写法)RBTree<K, V>& operator=(RBTree<K, V> t){swap(_root, t._root);return *this;}//析构函数~RBTree(){_Destroy(_root);_root = nullptr;}//查找函数Node* Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_kv.first) //key值小于该结点的值{cur = cur->_left; //在该结点的左子树当中查找}else if (key > cur->_kv.first) //key值大于该结点的值{cur = cur->_right; //在该结点的右子树当中查找}else //找到了目标结点{return cur; //返回该结点}}return nullptr; //查找失败}//插入函数pair<Node*, bool> Insert(const pair<K, V>& kv){if (_root == nullptr) //若红黑树为空树,则插入结点直接作为根结点{_root = new Node(kv);_root->_col = BLACK; //根结点必须是黑色return make_pair(_root, true); //插入成功}//1、按二叉搜索树的插入方法,找到待插入位置Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first < cur->_kv.first) //待插入结点的key值小于当前结点的key值{//往该结点的左子树走parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first) //待插入结点的key值大于当前结点的key值{//往该结点的右子树走parent = cur;cur = cur->_right;}else //待插入结点的key值等于当前结点的key值{return make_pair(cur, false); //插入失败}}//2、将待插入结点插入到树中cur = new Node(kv); //根据所给值构造一个结点Node* newnode = cur; //记录新插入的结点(便于后序返回)if (kv.first < parent->_kv.first) //新结点的key值小于parent的key值{//插入到parent的左边parent->_left = cur;cur->_parent = parent;}else //新结点的key值大于parent的key值{//插入到parent的右边parent->_right = cur;cur->_parent = parent;}//3、若插入结点的父结点是红色的,则需要对红黑树进行调整while (parent && parent->_col == RED){Node* grandfather = parent->_parent; //parent是红色,则其父结点一定存在if (parent == grandfather->_left) //parent是grandfather的左孩子{Node* uncle = grandfather->_right; //uncle是grandfather的右孩子if (uncle && uncle->_col == RED) //情况1:uncle存在且为红{//颜色调整parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}else //情况2+情况3:uncle不存在 + uncle存在且为黑{if (cur == parent->_left){RotateR(grandfather); //右单旋//颜色调整grandfather->_col = RED;parent->_col = BLACK;}else //cur == parent->_right{RotateLR(grandfather); //左右双旋//颜色调整grandfather->_col = RED;cur->_col = BLACK;}break; //子树旋转后,该子树的根变成了黑色,无需继续往上进行处理}}else //parent是grandfather的右孩子{Node* uncle = grandfather->_left; //uncle是grandfather的左孩子if (uncle && uncle->_col == RED) //情况1:uncle存在且为红{//颜色调整uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}else //情况2+情况3:uncle不存在 + uncle存在且为黑{if (cur == parent->_left){RotateRL(grandfather); //右左双旋//颜色调整cur->_col = BLACK;grandfather->_col = RED;}else //cur == parent->_right{RotateL(grandfather); //左单旋//颜色调整grandfather->_col = RED;parent->_col = BLACK;}break; //子树旋转后,该子树的根变成了黑色,无需继续往上进行处理}}}_root->_col = BLACK; //根结点的颜色为黑色(可能被情况一变成了红色,需要变回黑色)return make_pair(newnode, true); //插入成功}private://拷贝树Node* _Copy(Node* root, Node* parent){if (root == nullptr){return nullptr;}Node* copyNode = new Node(root->_data);copyNode->_parent = parent;copyNode->_left = _Copy(root->_left, copyNode);copyNode->_right = _Copy(root->_right, copyNode);return copyNode;}//析构函数子函数void _Destroy(Node* root){if (root == nullptr){return;}_Destroy(root->_left);_Destroy(root->_right);delete root;}//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;Node* parentParent = parent->_parent;//建立subRL与parent之间的联系parent->_right = subRL;if (subRL)subRL->_parent = parent;//建立parent与subR之间的联系subR->_left = parent;parent->_parent = subR;//建立subR与parentParent之间的联系if (parentParent == nullptr){_root = subR;_root->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* parentParent = parent->_parent;//建立subLR与parent之间的联系parent->_left = subLR;if (subLR)subLR->_parent = parent;//建立parent与subL之间的联系subL->_right = parent;parent->_parent = subL;//建立subL与parentParent之间的联系if (parentParent == nullptr){_root = subL;_root->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}}//左右双旋void RotateLR(Node* parent){RotateL(parent->_left);RotateR(parent);}//右左双旋void RotateRL(Node* parent){RotateR(parent->_right);RotateL(parent);}Node* _root; //红黑树的根结点
};相关文章:

【红黑树】
红黑树 小杨 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍&am…...

排序算法——简单选择排序
一、算法原理 简单选择排序是一种基本的排序算法,其原理是每次从未排序的元素中选择最小(或最大)的元素,然后与未排序部分的第一个元素交换位置,直到所有元素都被排序。 二、算法实现流程 简单选择排序法(Simple Se…...
OpenAI API推出结构化输出功能
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
Python 异步编程:Sqlalchemy 异步实现方式
SQLAlchemy 是 Python 中最流行的数据库工具之一,在新版本中引入了对异步操作的支持。这为使用异步框架(如 FastAPI)开发应用程序带来了极大的便利。在这篇文章中,简单介绍下 SQLAlchemy 是如何利用 Greenlet 实现异步操作的。 什…...

父类引用指向子类对象
在 Java 中,父类引用可以指向子类对象,这是多态的一种表现。这种特性允许你使用父类的引用来操作子类对象,从而实现更灵活和可扩展的代码设计。 基本概念 多态:父类引用可以指向子类对象。这使得你可以用统一的接口处理不同的对象…...
分享一个基于Spring Boot的面向社区的智能化健康管理系统的设计与实现(源码、调试、LW、开题、PPT)
💕💕作者:计算机源码社 💕💕个人简介:本人 八年开发经验,擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等,大家有这一块的问题可以一起交流&…...

【扒代码】reduction参数是什么
model DensityMapRegressor(in_channels256, reduction8)reduction 参数在 DensityMapRegressor 类中用于决定模型在上采样过程中的层级配置。具体来说,它决定了上采样过程中使用多少个 UpsamplingLayer,从而影响输出的分辨率。 reduction 参数的作用 …...
Python,Spire.Doc模块,处理word、docx文件,极致丝滑
Python处理word文件,一般都是推荐的Python-docx,但是只写出一个,一句话的文件,也没有什么样式,就是36K。 再打开word在另存一下,就可以到7-8k,我想一定是python-docx的问题,但一直没…...

redis的安装与命令
一、redis与memcache总体对比 1.性能 Redis:只使用单核,平均每一个核上Redis在存储小数据时比Memcached性能更高。 Memcached:可以使用多核,而在100k以上的数据中,Memcached性能要高于Redis。 2.内存使用效率 Mem…...

【C++】特殊类设计类型转换
目录 💡前言一,特殊类设计1. 请设计一个类,不能被拷贝2. 请设计一个类,只能在堆上创建对象3. 请设计一个类,只能在栈上创建对象4. 请设计一个类,不能被继承5. 请设计一个类,只能创建一个对象(单…...

为git 命令行 设置代理环境变量
http://t.csdnimg.cn/cAxkg 国内需要修改pinoko根目录下gitconfig文件,添加 [http]proxy http://127.0.0.1:1080 [https]proxy https://127.0.0.1:1080或者通过命令行配置: git config --global http.proxy http://127.0.0.1:1080 git config --glo…...

自定义linux某些常见配置
1.当前路径 echo "PS1\u\h:\w\$ " >> /etc/profile source /etc/profile 2.ssh使能 1.开启openssh 2.权限赋予chown root.root /var/empty/ 3.开发板作为server echo "PermitRootLogin yes" >> /etc/ssh/sshd_config 3开机自启动脚本 1.init…...
告别手动操作!KeyMouseGo实现自动化工作流
前言 在这个快节奏的时代,我们每天都在与电脑打交道,重复着那些繁琐而单调的操作;你是否曾想过,能让电脑自己完成这些任务,而你则悠闲地喝着咖啡,享受着生活?今天,就让我们一起揭开一…...

大型语言模型微调 新进展-4篇 论文
1. Brevity is the soul of wit: Pruning long files for code generation 发布时间:2024-06-29链接:https://arxiv.org/abs/2407.00434机构:伦敦大学学院 (UCL) 本研究针对大型语言模型的代码生成任务中的数据清理问题进行了探索。研究发现…...
专业课140+杭电杭州电子科技大学843信号与系统考研经验电子信息与通信工程真题,大纲,参考书。
顺利上岸杭电,由于专业课考的不错140,群里不少同学希望分享一点经验,回头看看这一年考研复习,确实有得有失,总结一下自己的专业课复习经验,希望对大家有帮助,基础课考的没有专业好,而…...
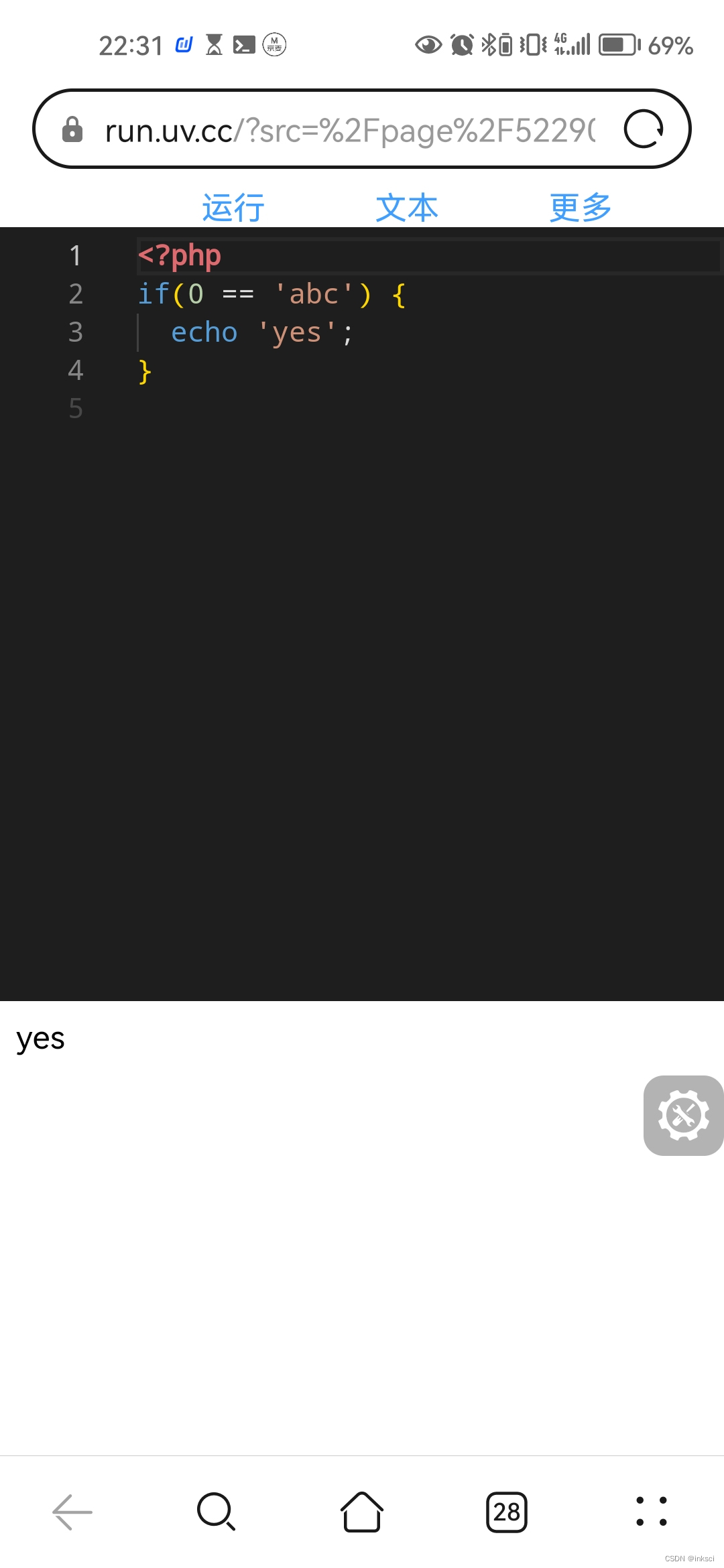
php 中 (0 == ‘abc‘) 为真
https://andi.cn/page/621653.html...
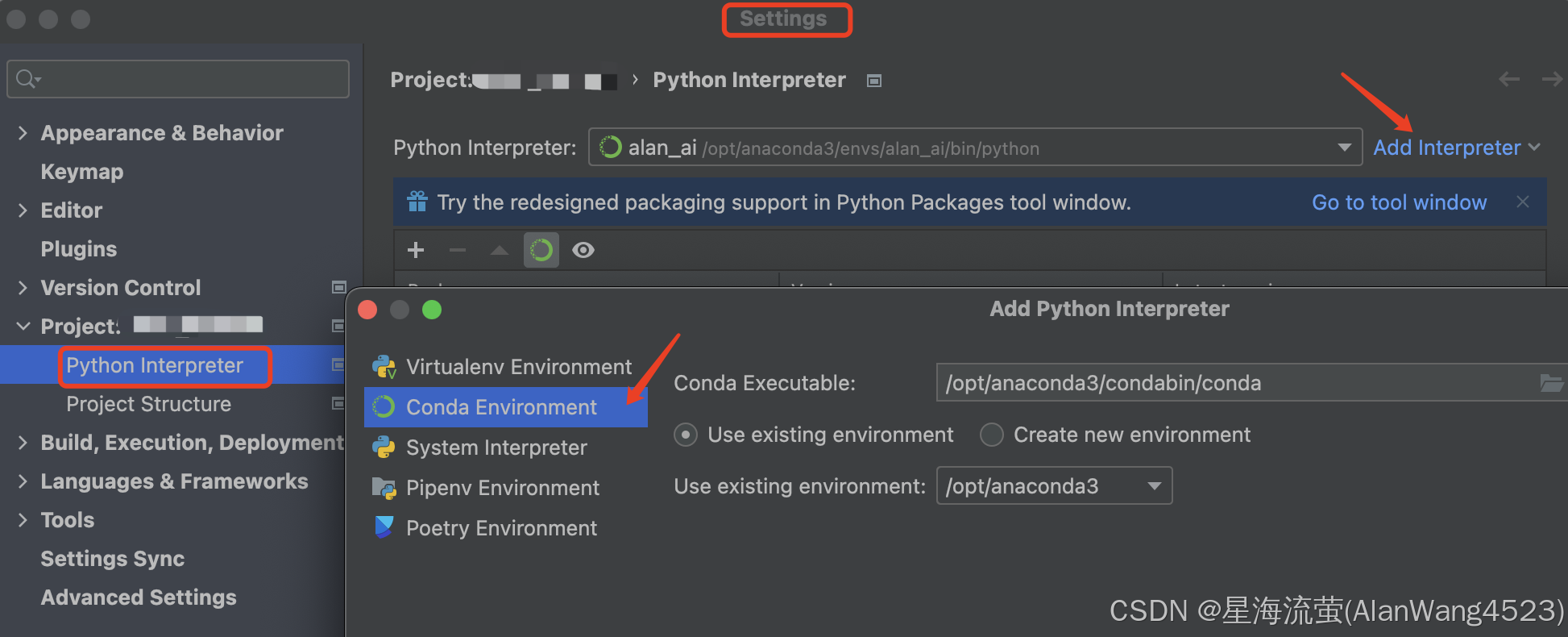
MacOS Anaconda 安装教程及虚拟环境创建
一、下载 Anaconda 1、Anaconda 官网 2、清华大学开源软件镜像站 点 Date 按时间排序,根据自己 Mac 芯片类型下载对应最新版本的。 Intel 芯片的下载 x86_64 版本的Apple m1 芯片的下载 arm64 版本的 二、安装 Anaconda 将安装包下载到本地后,双击安…...

Mac快速配置ADB环境变量
ADB是进行 Androd 开发时很常用的调试工具,Android SDK 中就包含了该工具,所以如果安装了SDK那只需要在环境变量中配置 Android SDK 的路径即可,本文的环境配置也基于这种场景。 如果需要独立下载 ADB 工具,请参考下面网址&#x…...

Kylin的工作原理及使用分享
前言 在当今信息爆炸的时代,企业和研究机构每天都在生成和收集大量的数据。这些数据中蕴藏着巨大的商业价值和研究潜力,但要从中提取出有用的信息却并非易事。传统的数据处理和分析技术在面对如此庞大的数据量时,往往难以提供快速和有效的响…...

python 使用seleniumwire获取响应数据
seleniumwire 是一个在 Selenium WebDriver 基础上扩展的库,它允许你在使用 Selenium 进行网页自动化测试或爬虫时捕获和修改 HTTP 请求和响应。这对于需要分析网页数据或进行更复杂的网络交互的自动化任务特别有用。 以下是如何使用 seleniumwire 来获取响应数据的…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
