WPF篇（11）-ToolTip控件（提示工具）+Popup弹出窗口

ToolTip控件

ToolTip控件继承于ContentControl，它不能有逻辑或视觉父级，意思是说它不能以控件的形式实例化，它必须依附于某个控件。因为它的功能被设计成提示信息，当鼠标移动到某个控件上方时，悬停一会儿，就会显示这个ToolTip的内容。

通常ToolTip会显示一句话，用来阐述某个控件的说明。这个控件存在于FrameworkElement基类中，也就是ToolTip属性，这个属性在FrameworkElement虽然被声明成object，而不是ToolTip类型，但是，我们仍然可以自定义ToolTip的内容。重点：WPF几乎所有控件都可以拥有ToolTip小型提示弹窗！

因为ToolTip继承于ContentControl控件，所以，ToolTip拥有的Content属性就可以显示任何类型，比如字符串、图像、其它控件组合布局。

简单使用

<Button Content="确定" ToolTip="ToolTip控件"/>

自定义ToolTip内容

前端代码

        <Button x:Name="button2" Content="百度一下" Width="100" Height="30" Margin="5" Click="button2_Click"><Button.ToolTip><StackPanel><TextBlock Text="官方网站" FontWeight="Bold" /><TextBlock Text="点击这个按钮，进入百度首页"/><Border BorderBrush="Silver" BorderThickness="0,1,0,0" Margin="0,4"/><TextBlock Text="http://www.baidu.com" Foreground="Blue" FontStyle="Italic"/></StackPanel></Button.ToolTip></Button>

后端代码

        private void button2_Click(object sender, RoutedEventArgs e){Process.Start("http://www.baidu.com");}

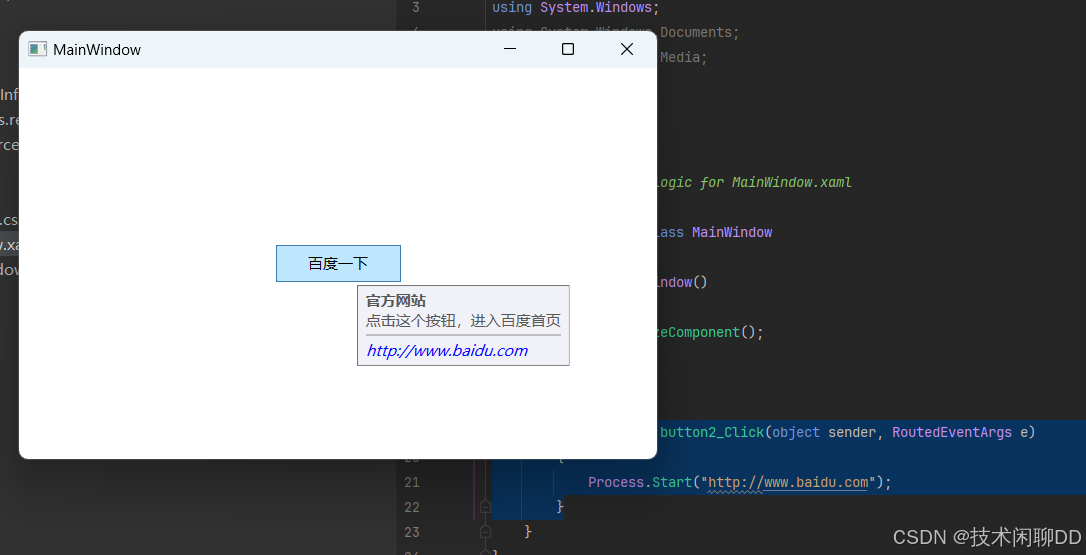
注意：

• 虽然ToolTip可以自定义内容，但是，ToolTip的内容无法接收焦点。

• 与ToolTip有点类似的控件，还有一个叫Popup控件，也是一个弹出窗口，并可以在这个窗口内任意布局。后面我们会学到。

Popup弹出窗口

Popup类似于ToolTip，在指定的元素或窗体中弹出一个具有任意内容的窗口。

属性成员

• HasDropShadow：只读属性，控件是否有投影效果。
• AllowsTransparency：获取或设置控件是否包含透明内容。
• PopupAnimation：获取或设置控件打开或关闭时的动画效果，None表示没有动画，Fade表示逐渐显示或淡出，Slide表示向上向下滑入，Scroll表示滚动效果。
• PlacementRectangle ：获取或设置控件打开时的矩形位置 。
• PlacementTarget： 获取或设置Popup控件在哪个控件身边打开（重点）。
• VerticalOffset ：获取或设置目标原点和 popup 对齐点之间的垂直距离。
• HorizontalOffset ：获取或设置目标原点和弹出项对齐之间的水平距离点。
• StaysOpen ：默认值为true，表示Popup打开后，如果失去焦点，Popup是否继续显示（重点）。
• Child ：获取或设置控件的内容，类似于ContentControl的Content属性，只能拥有一个元素（重点）。
• IsOpen ：获取或设置Popup控件是否可见。
• Placement ：枚举类，表示Popup 控件显示时的对齐方式。

事件成员

• Opened事件：Popup控件打开时引发的事件。

• Closed事件：Popup控件关闭时引发的事件。

案例

<StackPanel Orientation="Horizontal" HorizontalAlignment="Center" VerticalAlignment="Center"><CheckBox x:Name="checkbox" Content="百度一下" Height="30" Margin="5" ToolTip="百度一下，你就知道"/><Popup Name="myPopup" IsOpen="{Binding IsChecked, ElementName=checkbox}" PlacementTarget="{Binding ElementName=checkbox}" StaysOpen="True"><Border BorderThickness="1" Background="LightBlue"><StackPanel><TextBlock Text="官方网站" FontWeight="Bold" /><TextBlock Text="点击这个按钮，进入百度首页"/><Border BorderBrush="Silver" BorderThickness="0,1,0,0" Margin="0,4"/><TextBlock Text="http://www.baidu.com" FontStyle="Italic"/></StackPanel></Border></Popup></StackPanel>

我们分别实例化了名叫checkbox和myPopup控件，myPopup的IsOpen属性绑定了checkbox的IsChecked，意思是， 当用户点击checkbox时，checkbox的IsChecked属性为true，myPopup的IsOpen属性也为true，于是就可以显示myPopup的内容了。

同时，myPopup的PlacementTarget属性也绑定到了checkbox控件，意味着myPopup将显示在checkbox控件身边。