高等数学 第九讲 一元函数积分学的应用
1. 一元函数积分学的应用
文章目录
- 1. 一元函数积分学的应用
- 1. 几何应用
- 1.1 用定积分表达和计算平面图形的面积
- 1.2 用定积分表达和计算旋转体的体积
- 1.2.1 微分法
- 1.2.2 二重积分法
- 1.2.3 古尔丁定理
- 1.2.4 旋转体的体积公式总结
- 1.3 用定积分表达和计算函数的平均数
- 1.4 其他几何应用
- 1.4.1 "平面上的曲边梯形"的形心坐标公式
- 1.4.2 平面曲线的弧长
- 1.4.3 旋转曲面的面积(侧面积)
- 公式使用小总结
- 2. 积分等式与积分不等式(待整理)
- 3.物理应用
- 3.1 变力沿直线做功
- 3.2 抽水做功
- 3.3 静水压力
1. 几何应用
1.1 用定积分表达和计算平面图形的面积
三大体系下的图形,直角坐标系和极坐标系直接计算,参数方程转换为直角坐标系再进行计算。
下面给出平面直角坐标系和极坐标系下两条曲线所围成平面图形的面积:

(2)的解释说明:
扇形面积,dθ趋近于0,看成90度,阴影部分面积看成三角形 1/2底*高
高是r2,底是弧长,弧长=顶角✖️边长=dθ✖️r2,故 1/2✖️r2dθ *r2=1/2 r22dθ
1.2 用定积分表达和计算旋转体的体积
虽然下面给出了公式,但是在具体做题中,发现用处不大,后续冲刺更新复习中,会删掉多余的公式
1.2.1 微分法
经典的做法,但是只能较为有效解决绕x轴,y轴的旋转体的体积,不太推荐。
1.2.2 二重积分法
方法来源于:武忠祥高等数学辅导讲义,利用二重积分来解决旋转体体积的问题。
核心思想:拿出待求面积内的一个小面积记作dσ,将这个小面积旋转,剪开,发现是一个圆柱体,圆柱体体积=底面积*高,底面积就是dσ,高是没剪开的甜甜圈的周长,2派r,其中这个r是,点(x,y)到旋转直线的距离,有公式。
综上,
v = 底面积 ∗ 高 = ∬ D d σ ∗ 2 π r ( x , y ) = 2 π ∬ D r ( x , y ) d σ v = 底面积*高 = \iint \limits_{D}^{}d\sigma *2\pi r\left(x,y\right) = 2\pi \iint \limits_{D}^{}r\left(x,y\right)d\sigma v=底面积∗高=D∬dσ∗2πr(x,y)=2πD∬r(x,y)dσ
1.2.3 古尔丁定理

利用第一个古尔丁定理的结论,我们不难得出,重点在于计算形心计算形心有公式。然后在根据点到直线的距离或者观察法计算形心到转轴的距离。
1.2.4 旋转体的体积公式总结
定积分计算旋转体体积公式:

(2)的解释说明:
薄壁柱体(壳体),切开展开得到一个长方体,高是|y(x)|,宽是dx,长是圆的周长2派r,r就是x,故是2派x,长方体体积=长宽高=2派x|y(x)|dx
(3)平面曲线绕定直线旋转

如何使用,就是做差使用,两条曲线围成面积,绕着旋转,就分别求如何作差。
1.3 用定积分表达和计算函数的平均数

1.4 其他几何应用
1.4.1 "平面上的曲边梯形"的形心坐标公式


1.4.2 平面曲线的弧长
三个公式都得背
关于计算弧长时,积分上下限怎么确定,积分下限必是小的,上限必是大的
1.4.3 旋转曲面的面积(侧面积)
先记第一个
综上可知,弧长和侧面积都得保证上下限从小到大
公式使用小总结
在计算面积,体积,弧长,侧面积时,我们会求直角坐标系下的就行,其他坐标系都可以通过换元法转换为直角坐标系。
注意换元有三换,还有就是直角坐标系下的y’,是对应参数方程的dy/dx,也就是 (dy/dt)/(dx/dt)
极坐标系其实也是参数方程,x=rcosθ,y=rsinθ
2. 积分等式与积分不等式(待整理)
3.物理应用
3.1 变力沿直线做功

3.2 抽水做功
物理知识补充既公式推导:
抽水做功公式:w=F浮h,每一块的h其实就是横坐标,看图,故w=F浮x,当前进度:w=F浮x
浮力公式:ρgv,v是体积,重点在于确定v,当前进度:w=ρgvx
v是水面一层(类似于硬币)的体积,看成圆柱体,圆柱体v=底面积*高,底面积设为A(x),故v=A(x)dx,当前进度:w=ρgA(x)xdx
故总结公式为求积分a到b上的w,a是水面,b是水底
问题的关键在于确定x处水平截面面积A(x),其余的量都是固定的。故拿到题核心在于求A(x)

3.3 静水压力
物理知识补充既公式推导:
压强公式=压力/横截面面积,故压力=压强横截面面积
横截面面积=长宽,长是f(x)-g(x),宽是dx
压强=pgh=pgx,故公式得证
求解关键是平板的宽度f(x)-h(x)

相关文章:

高等数学 第九讲 一元函数积分学的应用
1. 一元函数积分学的应用 文章目录 1. 一元函数积分学的应用1. 几何应用1.1 用定积分表达和计算平面图形的面积1.2 用定积分表达和计算旋转体的体积1.2.1 微分法1.2.2 二重积分法1.2.3 古尔丁定理1.2.4 旋转体的体积公式总结 1.3 用定积分表达和计算函数的平均数1.4 其他几何应…...

django如何更新数据库字段并与数据库保持同步?
关键步骤: 第一步: 执行:python manage.py makemigrations 你的项目名称第二步:它会提示你选1还是2,这里因为添加字段,所以选1第三步:出现>>>这个,直接输入这个第四步&am…...

jenkins插件 SSH Publishers
Jenkins 是一个开源的自动化服务器,常用于持续集成和持续交付 (CI/CD)。以下是一些与 Jenkins 相关的 SSH 发布者及其功能: SSH 插件: 功能: 允许 Jenkins 通过 SSH 执行远程命令。用户可以配置 SSH 服务器,使用 SSH 密钥进行身份…...

Kafka Client客户端操作详解
文章目录 基础客户端版本消息生产者消息消费者踩坑 客户端属性分析消费者分组消费机制生产者拦截器消息序列化消息分区路由机制生产者消息缓存机制发送应答机制生产者消息幂等性生产者消息事务 客户端流程总结 基础客户端版本 导入依赖 <properties><project.build.…...

【HarmonyOS NEXT星河版开发学习】小型测试案例15-博客列表
个人主页→VON 收录专栏→鸿蒙开发小型案例总结 基础语法部分会发布于github 和 gitee上面(暂未发布) 前言 该案例主要是ForEach渲染的练习,ForEach可以基于数组的个数,渲染组件个数(简化代码) 在…...

go-zero中统一返回前端数据格式的几种方式
方式一、直接定义一个成功和失败的方法,在代码里面修改(对代码有侵入,每次都要修改代码) 1、封装一个统一返回的方法 package utilsimport ("github.com/zeromicro/go-zero/rest/httpx""net/http" )type Body struct {Code int json:"code…...

【向量数据库】Ubuntu编译安装FAISS
参考官方的安装指导:https://github.com/facebookresearch/faiss/blob/main/INSTALL.md,不需要安装的可以跳过 ~$ wget https://github.com/facebookresearch/faiss/archive/refs/tags/v1.8.0.tar.gz ~$ tar -zxvf v1.8.0.tar.gz ~$ cd faiss-1.8.0 ~$ …...
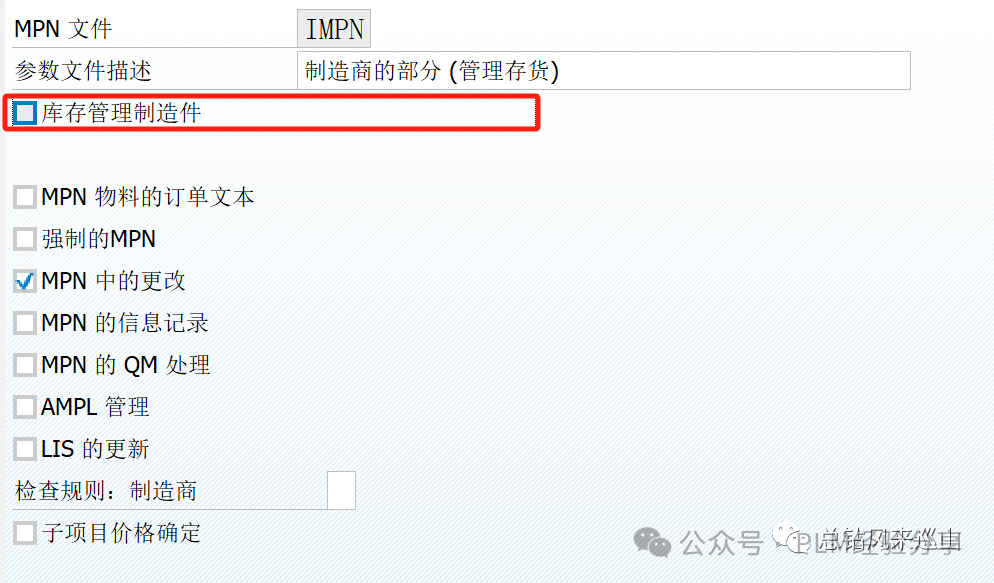
制造知识普及(九)--企业内部物料编码(IPN)与制造商物料编码(MPN)
在日常的物料管理业务逻辑中,一物一码是物料管理的基本的业务规则,不管物料从产品开发还是仓库管理,甚至成本核算,都要遵循这个原则,才能保证产品数据的准确性,才具备唯一追溯的可行性。大部分企业都是这种…...

【整数规划】+【0—1规划】解决优化类问题(Matlab代码)
目录 文章目录 前言 一、整数规划 分类: 二、典例讲解 1.背包问题 2.指派问题 总结 前言 如果觉得本篇文章还不错的话,给作者点个赞鼓励一下吧😁😁😁 在规划问题中,有些最优解可能是分数或小数&am…...

Linux下如何使用Curl进行网络请求
在Linux系统上,Curl是一个非常强大的网络请求工具,可以用于发送各种类型的HTTP请求,并获取响应结果。它支持常见的HTTP方法,如GET、POST、PUT、DELETE等,还支持HTTPS、FTP等不同协议。Curl提供了丰富的参数选项&#x…...

PostgreSQL 触发器
PostgreSQL 触发器 PostgreSQL触发器是一种强大的数据库对象,它可以在特定的数据库事件发生时自动执行预定义的操作。这些事件可以是插入、更新或删除表中的行。触发器通常用于强制复杂的业务规则、提供审计跟踪、数据同步以及实现复杂的约束。 触发器的基本概念 …...

LeetCode——3131.找出与数组相加的整数I
通过万岁!!! 题目:给你两个数组nums1和nums2,然后让你找一个数,使得nums1的数加上这个数以后得到的数组nums1’与nums2是相同的。注意这里只要元素相同就好了,不一定顺序相同。思路:…...

【SpringMVC】详细了解SpringMVC中WEB-INF 目录资源,视图解析器和静态资源放行的使用。
目录 1. 回顾SpringMVC请求转发和重定向 2. WEB-INF资源目录 3. 视图解析器 4. 静态资源放行 1. 回顾SpringMVC请求转发和重定向 概念:在一个项目中功能非常多,也就意味着有非常多的Servlet,不同的Servlet的职不 同 ,而用户发起…...

如何学好uni-app
学习uni-app需要掌握以下技能: 1. 前端基础:熟悉HTML、CSS和JavaScript等前端开发技术,了解基本的前端框架如Vue.js。 2. Vue.js:因为uni-app是基于Vue.js构建的,所以需要对Vue.js有深入的理解。可以先通过官方文档或者…...

C++ QT使用stackwidget实现页面切换(含源码)
C++ QT使用stackwidget实现页面切换(含源码) 0.前言1.UI布局1.1使用stackwidget2.代码方式添加页面实现页面切换3.源码4.最终效果0.前言 在QT中一个界面中如何实现页面的切换,而不是新弹出的窗口,这里采用的stackwidget,以层叠widget的方式选定页面索引从而实现页面切换。…...

打工人上班适合用的蓝牙耳机推荐?几款开放式耳机推荐
日常工作的话,我还是比较推荐开放式蓝牙耳机的,它特别适合那些需要在长时间工作中保持专注和舒适度的环境,那开放式耳机其实还有一些主要的优点: 减少耳朵疲劳:由于开放式耳机不需要紧密贴合耳朵,因此可以…...
一款.NET开发的AI无损放大工具
一款.NET开发的AI无损放大工具 思维导航 前言项目功能支持语言系统要求项目源代码项目运行小图片进行无损放大项目源码地址优秀项目和框架精选 前言 今天大姚给大家分享一款由.NET开源(GPL-3.0 license)、基于腾讯ARC Lab提供的Real-ESRGAN模型开发的A…...

编程新手必看:彻底理解!与~的取反操作
在编程和计算机科学的语境中,! 和 ~ 都是取反操作符,但它们的应用方式和效果存在显著的区别。下面将从定义、应用场景、作用原理及示例等方面对 ! 和 ~ 进行详细解析。 一、定义 !(逻辑非运算符) 在C语言、Java等多数编程语言中&…...

【LeetCode】54. 螺旋矩阵
螺旋矩阵 题目描述: 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2:…...

计算机毕业设计 奖学金评定管理系统 Java+SpringBoot+Vue 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...




