动手学深度学习7.3 网络中的网络(NiN)-笔记练习(PyTorch)
以下内容为结合李沐老师的课程和教材补充的学习笔记,以及对课后练习的一些思考,自留回顾,也供同学之人交流参考。
本节课程地址:26 网络中的网络 NiN【动手学深度学习v2】_哔哩哔哩_bilibili
本节教材地址:7.3. 网络中的网络(NiN) — 动手学深度学习 2.0.0 documentation (d2l.ai)
本节开源代码:...>d2l-zh>pytorch>chapter_multilayer-perceptrons>nin.ipynb
网络中的网络(NiN)
LeNet、AlexNet和VGG都有一个共同的设计模式:通过一系列的卷积层与汇聚层来提取空间结构特征;然后通过全连接层对特征的表征进行处理。 AlexNet和VGG对LeNet的改进主要在于如何扩大和加深这两个模块。 或者,可以想象在这个过程的早期使用全连接层。然而,如果使用了全连接层,可能会完全放弃表征的空间结构。 网络中的网络(NiN)提供了一个非常简单的解决方案:在每个像素的通道上分别使用多层感知机 (href="https://zh.d2l.ai/chapter_references/zreferences.html#id93">Linet al., 2013)。
(NiN块)
回想一下,卷积层的输入和输出由四维张量组成,张量的每个轴分别对应样本、通道、高度和宽度。 另外,全连接层的输入和输出通常是分别对应于样本和特征的二维张量。 NiN的想法是在每个像素位置(针对每个高度和宽度)应用一个全连接层。 如果我们将权重连接到每个空间位置,我们可以将其视为 1×1 卷积层(如6.4节 中所述),或作为在每个像素位置上独立作用的全连接层。 从另一个角度看,即将空间维度中的每个像素视为单个样本,将通道维度视为不同特征(feature)。
图7.3.1 说明了VGG和NiN及它们的块之间主要架构差异。 NiN块以一个普通卷积层开始,后面是两个1×1 的卷积层。这两个 1×1 卷积层充当带有ReLU激活函数的逐像素全连接层。 第一层的卷积窗口形状通常由用户设置。 随后的卷积窗口形状固定为 1×1。

7.3.1 对比 VGG 和 NiN 及它们的块之间主要架构差异。
import torch
from torch import nn
from d2l import torch as d2ldef nin_block(in_channels, out_channels, kernel_size, strides, padding):return nn.Sequential(nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),nn.ReLU(),nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())[NiN模型]
最初的NiN网络是在AlexNet后不久提出的,显然从中得到了一些启示。 NiN使用窗口形状为 11×11 、 5×5 和 3×3 的卷积层,输出通道数量与AlexNet中的相同。 每个NiN块后有一个最大汇聚层,汇聚窗口形状为3×3,步幅为2。
NiN和AlexNet之间的一个显著区别是NiN完全取消了全连接层。 相反,NiN使用一个NiN块,其输出通道数等于标签类别的数量。最后放一个全局平均汇聚层(global average pooling layer),生成一个对数几率 (logits)。NiN设计的一个优点是,它显著减少了模型所需参数的数量。然而,在实践中,这种设计有时会增加训练模型的时间。
net = nn.Sequential(nin_block(1, 96, kernel_size=11, strides=4, padding=0),nn.MaxPool2d(3, stride=2),nin_block(96, 256, kernel_size=5, strides=1, padding=2),nn.MaxPool2d(3, stride=2),nin_block(256, 384, kernel_size=3, strides=1, padding=1),nn.MaxPool2d(3, stride=2),nn.Dropout(0.5),# 标签类别数是10nin_block(384, 10, kernel_size=3, strides=1, padding=1),nn.AdaptiveAvgPool2d((1, 1)),# 将四维的输出转成二维的输出,其形状为(批量大小,10)nn.Flatten())我们创建一个数据样本来[查看每个块的输出形状]。
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:X = layer(X)print(layer.__class__.__name__,'output shape:\t', X.shape)输出结果:
Sequential output shape: torch.Size([1, 96, 54, 54])
MaxPool2d output shape: torch.Size([1, 96, 26, 26])
Sequential output shape: torch.Size([1, 256, 26, 26])
MaxPool2d output shape: torch.Size([1, 256, 12, 12])
Sequential output shape: torch.Size([1, 384, 12, 12])
MaxPool2d output shape: torch.Size([1, 384, 5, 5])
Dropout output shape: torch.Size([1, 384, 5, 5])
Sequential output shape: torch.Size([1, 10, 5, 5])
AdaptiveAvgPool2d output shape: torch.Size([1, 10, 1, 1])
Flatten output shape: torch.Size([1, 10])
[训练模型]
和以前一样,我们使用Fashion-MNIST来训练模型。训练NiN与训练AlexNet、VGG时相似。
lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())输出结果:
loss 0.352, train acc 0.871, test acc 0.874
1721.5 examples/sec on cuda:0

小结
- NiN使用由一个卷积层和多个 1×1 卷积层组成的块。该块可以在卷积神经网络中使用,以允许更多的每像素非线性。
- NiN去除了容易造成过拟合的全连接层,将它们替换为全局平均汇聚层(即在所有位置上进行求和)。该汇聚层通道数量为所需的输出数量(例如,Fashion-MNIST的输出为10)。
- 移除全连接层可减少过拟合,同时显著减少NiN的参数。
- NiN的设计影响了许多后续卷积神经网络的设计。
练习
- 调整NiN的超参数,以提高分类准确性。
解:
代码如下:
lr, num_epochs, batch_size = 0.05, 20, 128
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())输出结果:
loss 0.281, train acc 0.896, test acc 0.885
1719.9 examples/sec on cuda:0

2. 为什么NiN块中有两个 1×1 卷积层?删除其中一个,然后观察和分析实验现象。
解:
第一个 1×1 卷积层作用是降维:用于减少特征图的通道数,从而降低网络的参数数量和计算复杂度,有助于防止过拟合,并使网络更加高效。
第二个 1×1 卷积层作用是增加网络深度和像素的非线性性:对第一个卷积层的输出进行非线性变换,有助于网络学习更复杂的特征表示。通过这种方式,网络可以在保持参数数量相对较低的同时,增加其表达能力。
同时,1×1 卷积层可以融合每个像素点不同通道的特征,因此也具有特征融合的作用。
删除其中一个 1×1 卷积层后,训练损失略上升,训练和测试精度略下降,可能导致网络学习特征能力下降、非线性性降低,从而导致精度略下降。
def nin_block(in_channels, out_channels, kernel_size, strides, padding):return nn.Sequential(nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),nn.ReLU(),nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())
lr, num_epochs, batch_size = 0.1, 10, 128
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())输出结果:
loss 0.360, train acc 0.867, test acc 0.869
2208.1 examples/sec on cuda:0

3. 计算NiN的资源使用情况。
1)参数的数量是多少?
2)计算量是多少?
3)训练期间需要多少显存?
4)预测期间需要多少显存?
解:
计算过程如下:

对于一张图(1, 224, 224)而言:
1)参数的数量为:1.92 MB;
2)计算量为:1.55 GB;
3)训练期间的显存为参数占用显存+模型占用显存:
参数占用显存:1.92 * 4 * 2 = 15.38 MB (float32占4 bytes,1 for params, 1 for SGD)
模型占用显存:6.35 * 4 * 2 = 50.80 MB (float32占4 bytes,1 for forward, 1 for backward)
总占用显存:15.38 + 50.80 = 66.18 MB
4)预测期间的显存为参数占用显存+模型占用显存:
参数占用显存:1.92 * 4 = 7.69 MB (float32占4 bytes,only for params)
模型占用显存:6.35 * 4 = 25.40 MB (float32占4 bytes,only for forward)
总占用显存:7.69 + 25.40 = 33.09 MB
4. 一次性直接将 384×5×5 的表示缩减为 10×5×5 的表示,会存在哪些问题?
解:
一次性直接将 384×5×5 的表示缩减为 10×5×5 的表示,即不经过两个 1×1 卷积层降维,可能存在的问题有:
1)可能会丢失大量的信息。
2)可能过拟合增大:当特征维度降低太多时,网络可能无法捕捉到足够的特征来泛化到新的数据上。
3)可能学习能力下降:大幅度降低特征维度会限制网络的学习能力,使其难以学习复杂的函数映射。
4)可能破坏特征融合:不同层的特征图会通过 卷积层进行融合,以提取更加抽象的特征。如果直接大幅度减少特征维度,可能会破坏这种特征融合的过程,影响网络性能。
5)可能会导致梯度消失或梯度爆炸。
相关文章:
动手学深度学习7.3 网络中的网络(NiN)-笔记练习(PyTorch)
以下内容为结合李沐老师的课程和教材补充的学习笔记,以及对课后练习的一些思考,自留回顾,也供同学之人交流参考。 本节课程地址:26 网络中的网络 NiN【动手学深度学习v2】_哔哩哔哩_bilibili 本节教材地址:7.3. 网络…...

SQL语言-select的使用方法
select语法的使用(SQLyog) 设定查询结果返回的行数 #设定查询结果返回的行数,需要使用limit,指定返回的行数 #格式:select 列名 from 表名 limit n; #n代表限定的行数 SELECT stu_name FROM student LIMIT 3;#格式&a…...

深入理解Python中的排序算法:快速排序与归并排序实现
深入理解Python中的排序算法:快速排序与归并排序实现 排序是计算机科学中一个基本而重要的操作,几乎在所有的编程任务中都会遇到。Python提供了内置的排序函数,但了解排序算法的实现原理对于提升编程能力和解决问题的能力至关重要。本文将深入探讨两种经典的排序算法:快速…...

Linux基础命令 ② 未完成
linux系统目录结构 解释 bin: 包含基本的可执行二进制文件,供所有用户使用。 boot: 存储操作系统启动所需的关键文件,如内核和初始化 RAM 磁盘(initramfs)。 dev: 包含设备节点,表示物理设备或虚拟设备。 etc: 存储…...

怎么加密文件?分享文件加密四个方法,2024新版操作教程,教你搞定!
数据的安全性与隐私保护显得尤为重要。 无论是个人敏感信息、企业商业机密还是创意作品,文件加密都是保障其不被未授权访问的重要手段。 本文将为您详细介绍四种文件加密方法,并附上2024年新版操作教程,助您轻松搞定文件加密,守护…...

cesium加载魔方立方体
cesium加载多个小立方体,组合拼成一个大立方体。 地理坐标拼合的大立方体有错位问题。必须进行坐标转换。 <template><div class"map"><div id"mapContainer" ref"mapContainer" class"map-container">&…...

unity 粒子系统学习
差不多了解了基本的ui面板,学一下粒子系统 取消轮廓线 这样粒子biubiu的时候就没有橙黄色的轮廓线了 三个子模块概念...

CogVideoX环境搭建推理测试
引子 智谱AI版Sora开源,首个可商用,18G显存即可运行。前文写了Open-Sora1.2的博文,感兴趣的童鞋请移步(Open-Sora1.2环境搭建&推理测试_open sora 1.2-CSDN博客)。对于这种占用资源少,且效果不错的多模…...
STL—容器—list【list的介绍和基本使用】【list的迭代器失效问题】
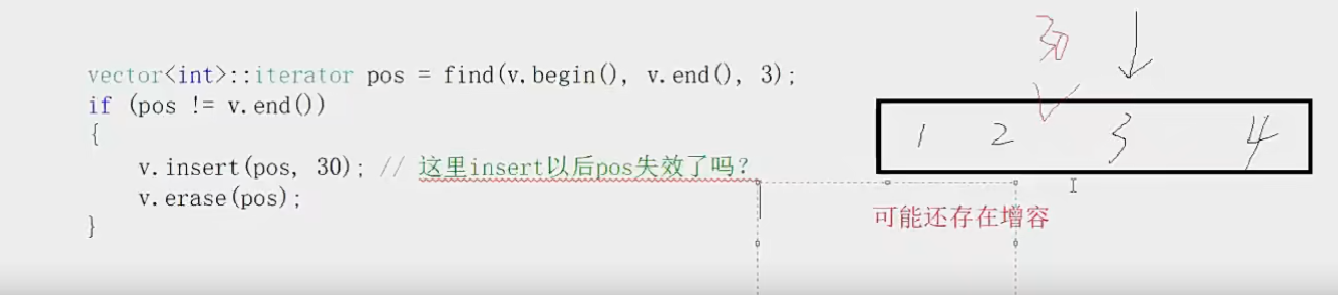
STL—容器—list list的使用并不难,有了之前使用string和vector的基础后,学习起来并不难。因此这里不在详细的讲解如何使用,而是大致的将其基本接口都熟悉一下 1.list介绍 list的文档介绍 list是可以在常数范围内在任意位置进行插入和删除…...

【面试宝典】MySQL 面试问题
一、MySQL 中有哪几种锁? MySQL中的锁机制是数据库并发控制的重要组成部分,它用于管理多个用户对数据库资源的访问,确保数据的一致性和完整性。MySQL中的锁可以根据不同的分类标准进行分类,以下是一些常见的分类方式及对应的锁类…...

【Cpp筑基】三、对象和类
【Cpp筑基】三、对象和类 Cpp系列笔记目录 【Cpp筑基】一、内联函数、引用变量、函数重载、函数模板 【Cpp筑基】二、声明 vs 定义、头文件、存储持续性作用域和链接性、名称空间 【Cpp筑基】三、对象和类 【Cpp筑基】四、重载运算符、友元、类的转换函数 【Cpp筑基】五、类的继…...

数据库原理面试-核心概念-问题理解
目录 1.数据库、数据库系统与数据库管理系统 2.理解数据独立性 3.数据模型 4.模式、外模式和内模式 5.关系和关系数据库 6.主键与外键 7.SQL语言 8.索引与视图 9.数据库安全 10.数据库完整性 11.数据依赖和函数依赖 12.范式?三范式?为什么要遵…...
方法)
【JavaScript】JavaScript里的“先斩后奏”之王 shift()方法
定义: JavaScript中 shift 方法用于删除数组的第一个元素,并返回该元素。注意,该方法会改变原数组! 解释: 成语解释: 先斩后奏是一个汉语成语,其拼音为xiān zhǎn hu zu。这个成语最早出自于汉班固的《汉书申屠嘉传》,原指先把罪犯处决,再向皇帝奏闻。在现代…...

Python面试宝典第32题:课程表
题目 你这个学期必须选修numCourses门课程,记为0到numCourses - 1。在选修某些课程之前,需要一些先修课程。先修课程按数组prerequisites给出,其中prerequisites[i] [ai, bi],表示如果要学习课程ai,则必须先学习课程b…...

简单介绍BTC的Layer2项目RGB
这里写自定义目录标题 介绍(历史背景,项目成员)核心技术组成部分一次性密封条(single-use-seals)客户端验证(client-side validation) 总结 注:该内容不构成投资建议,有些…...

跨境电商卖家必看:搭建安全稳定测评自养号环境系统
对于卖家而言,测评作为一种低成本、高回报的推广策略,对于提升产品流量、转化率、优化关键词质量分及增强链接权重等方面均发挥着积极作用。以下是自养号优势及测评环境搭建技术要点 一、搭建安全稳定的测评环境系统 核心要点: 硬件参数去…...
监控)
如何对open62541.h/open62541.c的UA_Client进行状态(在线/掉线)监控
文章目录 背景解决方案注意事项 背景 目前在利用open62541.h/open62541.c编写了一个与PLC进行OPCUA通讯的上位机程序。 上位机这边会定时对PLC的某个opcua变量进行写操作。但是假如PLC离线或者说拔掉网线,上位机就会直接崩溃死机,并且报如下的错误&…...

高等数学 第九讲 一元函数积分学的应用
1. 一元函数积分学的应用 文章目录 1. 一元函数积分学的应用1. 几何应用1.1 用定积分表达和计算平面图形的面积1.2 用定积分表达和计算旋转体的体积1.2.1 微分法1.2.2 二重积分法1.2.3 古尔丁定理1.2.4 旋转体的体积公式总结 1.3 用定积分表达和计算函数的平均数1.4 其他几何应…...

django如何更新数据库字段并与数据库保持同步?
关键步骤: 第一步: 执行:python manage.py makemigrations 你的项目名称第二步:它会提示你选1还是2,这里因为添加字段,所以选1第三步:出现>>>这个,直接输入这个第四步&am…...

jenkins插件 SSH Publishers
Jenkins 是一个开源的自动化服务器,常用于持续集成和持续交付 (CI/CD)。以下是一些与 Jenkins 相关的 SSH 发布者及其功能: SSH 插件: 功能: 允许 Jenkins 通过 SSH 执行远程命令。用户可以配置 SSH 服务器,使用 SSH 密钥进行身份…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
