cesium加载魔方立方体
cesium加载多个小立方体,组合拼成一个大立方体。
地理坐标拼合的大立方体有错位问题。必须进行坐标转换。

<template><div class="map"><div id="mapContainer" ref="mapContainer" class="map-container"></div><div class="map-other"><Steps progress-dot :current="currentVal" @change="changeStepsEvt"><Step title="1"></Step><Step title="2"></Step><Step title="3"></Step><Step title="4"></Step></Steps></div></div>
</template>
<script lang="ts" setup>
import { onMounted, ref } from 'vue';
import { Steps, Step } from 'ant-design-vue';
import * as THREE from 'three';
import { log } from 'console';
const currentVal = ref(0);
const win: AnyObject = window;
const Cesium = win.Cesium;
let viewer: any,cubeEntity: any = {};
let count = 0;
const init = () => {viewer = new Cesium.Viewer('mapContainer', {animation: false, //动画小部件baseLayerPicker: false, //地图图层组件infoBox: false, //信息框selectionIndicator: false, //选取指示器组件});// 获取CreditDisplay实例let creditDisplay = viewer.scene.frameState.creditDisplay;// 隐藏所有logocreditDisplay.show = false;// 立方体的边长const cubeSize = 100.0; // 100米边长// 第一个立方体的位置(成都经纬度,100米高度)const longitude = 104.0668;const latitude = 30.5728;const height = 100;const position1 = Cesium.Cartesian3.fromDegrees(longitude,latitude,height,);// 将地理坐标转换为局部坐标系const ellipsoid = viewer.scene.globe.ellipsoid;const origin = Cesium.Transforms.eastNorthUpToFixedFrame(position1,ellipsoid,);for (let i = 0; i < 3; i++) {for (let j = 0; j < 3; j++) {for (let k = 0; k < 3; k++) {const offset = new Cesium.Cartesian3(cubeSize * i,cubeSize * j,cubeSize * k,); // 在X轴上偏移const position = Cesium.Matrix4.multiplyByPoint(origin,offset,new Cesium.Cartesian3(),);cubeEntity[count] = viewer.entities.add({name: `Cube-${i}-${j}-${k}`,position: position,box: {dimensions: new Cesium.Cartesian3(cubeSize,cubeSize,cubeSize,),// material: Cesium.Color.fromRandom({ alpha: 1 }), // 半透明的蓝色material: Cesium.Color.fromBytes(177, 0, 4, 200), // 半透明的蓝色outline: true,outlineColor: Cesium.Color.WHITE,outlineWidth: 2,},});count++;}}}// 将视角调整到立方体的中心// viewer.zoomTo(viewer.entities);viewer.camera.flyTo({destination: Cesium.Cartesian3.fromDegrees(104.0658, 30.5682, 1200), // 目标位置和高度orientation: {heading: Cesium.Math.toRadians(30), // 相机航向角pitch: Cesium.Math.toRadians(-60), // 相机俯仰角roll: Cesium.Math.toRadians(0), // 相机滚转角},duration: 1, // 飞行持续时间(秒)});
};
onMounted(() => {init();
});
const colorList = [{color: Cesium.Color.fromBytes(177, 0, 4, 200),},{color: Cesium.Color.fromBytes(0, 206, 209, 200),},{color: Cesium.Color.fromBytes(106, 90, 205, 200),},{color: Cesium.Color.fromBytes(255, 255, 0, 100),},
];
const changeStepsEvt = (current) => {currentVal.value = current;for (let i = 0; i < count; i++) {cubeEntity[i].box.material = colorList[currentVal.value].color;}
};
setInterval(() => {currentVal.value++;if (currentVal.value >= 4) {currentVal.value = 0;}for (let i = 0; i < count; i++) {cubeEntity[i].box.material = colorList[currentVal.value].color;}
}, 3000);
</script>
<style lang="scss" scoped>
@import './index.scss';
</style>
相关文章:

cesium加载魔方立方体
cesium加载多个小立方体,组合拼成一个大立方体。 地理坐标拼合的大立方体有错位问题。必须进行坐标转换。 <template><div class"map"><div id"mapContainer" ref"mapContainer" class"map-container">&…...

unity 粒子系统学习
差不多了解了基本的ui面板,学一下粒子系统 取消轮廓线 这样粒子biubiu的时候就没有橙黄色的轮廓线了 三个子模块概念...

CogVideoX环境搭建推理测试
引子 智谱AI版Sora开源,首个可商用,18G显存即可运行。前文写了Open-Sora1.2的博文,感兴趣的童鞋请移步(Open-Sora1.2环境搭建&推理测试_open sora 1.2-CSDN博客)。对于这种占用资源少,且效果不错的多模…...
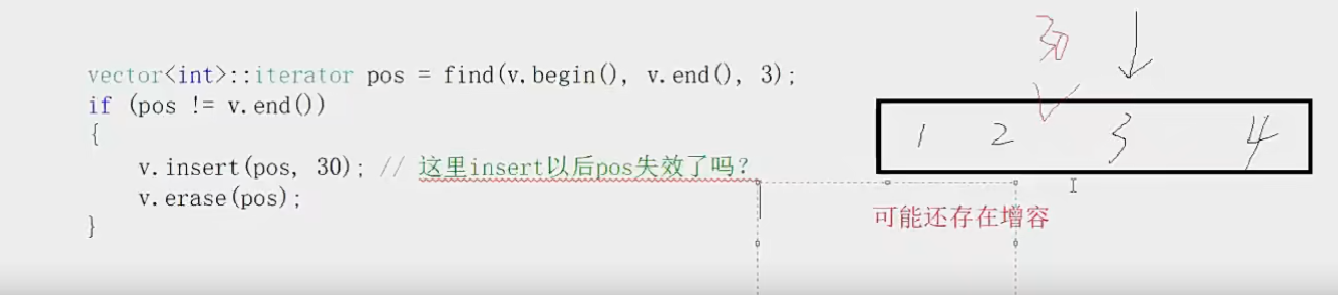
STL—容器—list【list的介绍和基本使用】【list的迭代器失效问题】
STL—容器—list list的使用并不难,有了之前使用string和vector的基础后,学习起来并不难。因此这里不在详细的讲解如何使用,而是大致的将其基本接口都熟悉一下 1.list介绍 list的文档介绍 list是可以在常数范围内在任意位置进行插入和删除…...

【面试宝典】MySQL 面试问题
一、MySQL 中有哪几种锁? MySQL中的锁机制是数据库并发控制的重要组成部分,它用于管理多个用户对数据库资源的访问,确保数据的一致性和完整性。MySQL中的锁可以根据不同的分类标准进行分类,以下是一些常见的分类方式及对应的锁类…...

【Cpp筑基】三、对象和类
【Cpp筑基】三、对象和类 Cpp系列笔记目录 【Cpp筑基】一、内联函数、引用变量、函数重载、函数模板 【Cpp筑基】二、声明 vs 定义、头文件、存储持续性作用域和链接性、名称空间 【Cpp筑基】三、对象和类 【Cpp筑基】四、重载运算符、友元、类的转换函数 【Cpp筑基】五、类的继…...

数据库原理面试-核心概念-问题理解
目录 1.数据库、数据库系统与数据库管理系统 2.理解数据独立性 3.数据模型 4.模式、外模式和内模式 5.关系和关系数据库 6.主键与外键 7.SQL语言 8.索引与视图 9.数据库安全 10.数据库完整性 11.数据依赖和函数依赖 12.范式?三范式?为什么要遵…...
方法)
【JavaScript】JavaScript里的“先斩后奏”之王 shift()方法
定义: JavaScript中 shift 方法用于删除数组的第一个元素,并返回该元素。注意,该方法会改变原数组! 解释: 成语解释: 先斩后奏是一个汉语成语,其拼音为xiān zhǎn hu zu。这个成语最早出自于汉班固的《汉书申屠嘉传》,原指先把罪犯处决,再向皇帝奏闻。在现代…...

Python面试宝典第32题:课程表
题目 你这个学期必须选修numCourses门课程,记为0到numCourses - 1。在选修某些课程之前,需要一些先修课程。先修课程按数组prerequisites给出,其中prerequisites[i] [ai, bi],表示如果要学习课程ai,则必须先学习课程b…...

简单介绍BTC的Layer2项目RGB
这里写自定义目录标题 介绍(历史背景,项目成员)核心技术组成部分一次性密封条(single-use-seals)客户端验证(client-side validation) 总结 注:该内容不构成投资建议,有些…...

跨境电商卖家必看:搭建安全稳定测评自养号环境系统
对于卖家而言,测评作为一种低成本、高回报的推广策略,对于提升产品流量、转化率、优化关键词质量分及增强链接权重等方面均发挥着积极作用。以下是自养号优势及测评环境搭建技术要点 一、搭建安全稳定的测评环境系统 核心要点: 硬件参数去…...
监控)
如何对open62541.h/open62541.c的UA_Client进行状态(在线/掉线)监控
文章目录 背景解决方案注意事项 背景 目前在利用open62541.h/open62541.c编写了一个与PLC进行OPCUA通讯的上位机程序。 上位机这边会定时对PLC的某个opcua变量进行写操作。但是假如PLC离线或者说拔掉网线,上位机就会直接崩溃死机,并且报如下的错误&…...

高等数学 第九讲 一元函数积分学的应用
1. 一元函数积分学的应用 文章目录 1. 一元函数积分学的应用1. 几何应用1.1 用定积分表达和计算平面图形的面积1.2 用定积分表达和计算旋转体的体积1.2.1 微分法1.2.2 二重积分法1.2.3 古尔丁定理1.2.4 旋转体的体积公式总结 1.3 用定积分表达和计算函数的平均数1.4 其他几何应…...

django如何更新数据库字段并与数据库保持同步?
关键步骤: 第一步: 执行:python manage.py makemigrations 你的项目名称第二步:它会提示你选1还是2,这里因为添加字段,所以选1第三步:出现>>>这个,直接输入这个第四步&am…...

jenkins插件 SSH Publishers
Jenkins 是一个开源的自动化服务器,常用于持续集成和持续交付 (CI/CD)。以下是一些与 Jenkins 相关的 SSH 发布者及其功能: SSH 插件: 功能: 允许 Jenkins 通过 SSH 执行远程命令。用户可以配置 SSH 服务器,使用 SSH 密钥进行身份…...

Kafka Client客户端操作详解
文章目录 基础客户端版本消息生产者消息消费者踩坑 客户端属性分析消费者分组消费机制生产者拦截器消息序列化消息分区路由机制生产者消息缓存机制发送应答机制生产者消息幂等性生产者消息事务 客户端流程总结 基础客户端版本 导入依赖 <properties><project.build.…...

【HarmonyOS NEXT星河版开发学习】小型测试案例15-博客列表
个人主页→VON 收录专栏→鸿蒙开发小型案例总结 基础语法部分会发布于github 和 gitee上面(暂未发布) 前言 该案例主要是ForEach渲染的练习,ForEach可以基于数组的个数,渲染组件个数(简化代码) 在…...

go-zero中统一返回前端数据格式的几种方式
方式一、直接定义一个成功和失败的方法,在代码里面修改(对代码有侵入,每次都要修改代码) 1、封装一个统一返回的方法 package utilsimport ("github.com/zeromicro/go-zero/rest/httpx""net/http" )type Body struct {Code int json:"code…...

【向量数据库】Ubuntu编译安装FAISS
参考官方的安装指导:https://github.com/facebookresearch/faiss/blob/main/INSTALL.md,不需要安装的可以跳过 ~$ wget https://github.com/facebookresearch/faiss/archive/refs/tags/v1.8.0.tar.gz ~$ tar -zxvf v1.8.0.tar.gz ~$ cd faiss-1.8.0 ~$ …...
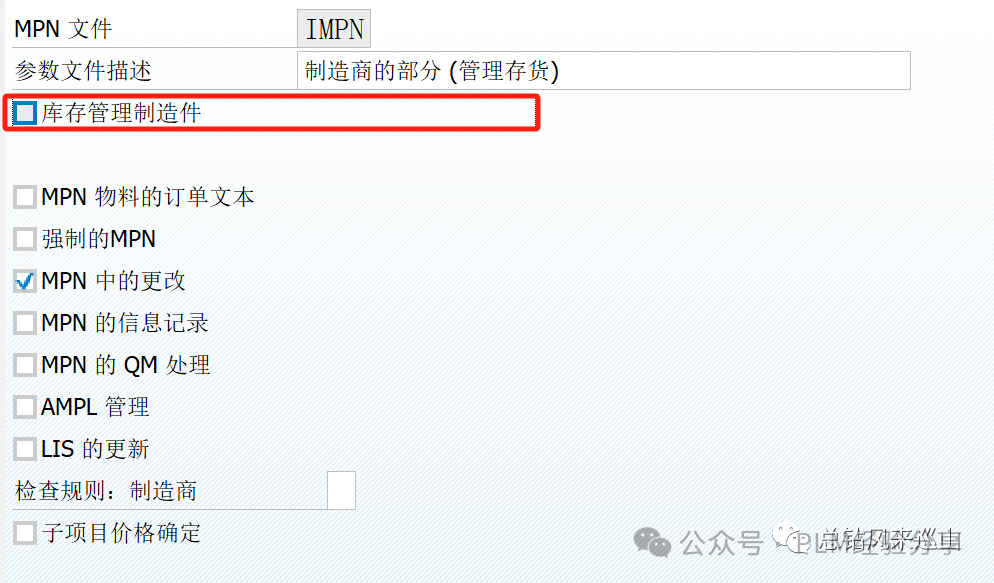
制造知识普及(九)--企业内部物料编码(IPN)与制造商物料编码(MPN)
在日常的物料管理业务逻辑中,一物一码是物料管理的基本的业务规则,不管物料从产品开发还是仓库管理,甚至成本核算,都要遵循这个原则,才能保证产品数据的准确性,才具备唯一追溯的可行性。大部分企业都是这种…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
