图算法系列1: 图算法的分类有哪些?(上)
大约在公元9世纪上半叶,来自中亚古国花剌子模的波斯数学家花剌子米(al-Khwarizmi)先后出版了两本对数学界有深远影响的书籍《印度数字算术》与《代数学》,前者在12世纪被翻译为拉丁文传入欧洲,十进制也因此传入欧洲,最终所形成的英文中的“算法”一词实际上是花剌子米的名字的拉丁文转译,后传入法国,大概在14世纪末传入英国,直至19世纪固定后形成了今天的“算法”一词。这个例子告诉我们,很多时候,人类的知识就像是通过一张“以讹传讹”的网络得以扩散和传播的。

所有的图算法在本质上都是对更为基础的图上的计算、分析与查询操作的高度概括与集成。那么,什么是基础的图上的计算、分析与查询操作呢?可以简单概括为以下两类操作。
❑ 面向元数据的低维、离散的操作。典型的例如面向顶点或边的聚合、排序等操作。
❑ 面向高维数据的操作。典型的例如路径、子图、网络查询以及图算法等操作。从图计算的视角,面向元数据的操作与之前所有SQL或NoSQL数据库没有本质区别,因此并不是本书的重点。
❑ 面向高维数据的操作,指的是从关联数据的角度,查询数据之间的关联关系、关联路径和影响力范围,例如我们常说的根因分析(Root-cause Analysis)、贡献度分析(ContributionAnalysis)、归因分析(Attribution Analysis)、影响力分析(Impact Analysis)、溯源分析(Backtracing)等。通过构建图数据模型,然后进行图上的查询与分析,通常会获得更高效、更灵活、更白盒化且更具可解释性的效果。
高维数据的查询有3个子类。
❑邻居查询:如最典型的k邻查询。
❑路径查询:如最短路径、环路、权重路径等。
❑展开、组网等其他较复杂查询:如从某顶点展开、多顶点组网等。
当然,所有的高维查询都可以通过拆解或分而治之的方式降维为低维查询,因为它们都是从某个或某类元数据(如顶点、边或其属性字段)开始操作的,而这些高维查询再进行组合、聚合、变形, 就形成了我们所谓的图算法。例如度算法中的全图入度查询,本质上就是计算所有顶点的入度。显然,在一张大图上,这个看似简单的算法的计算复杂度可能会非常高,如何进行加速就变成了重要的议题,我们会在第3章中进行详细分析。再比如全图k邻查询(k-Hop Neighbors,k跳邻居),在连通度较高的图中,即便是查询1个顶点的3跳、5跳邻居都可能会非常耗时(假如1个顶点的1跳邻居有20个,2跳邻居有400个,3跳邻居有8000个,而5跳邻居已经在3200000个的量级),如果有10000000个顶点,那么运行完这个算法的耗时和复杂度将是天文量级的。不经优化的图算法很多都是不具备实用性的,而优化可以获得指数级的性能提升与耗时降低—可能原来需要运行1个月的算法,如果在不增加硬件投入的前提下能提速1000倍,降低至0.7h(约40min)内完成,其意义是不言而喻的!这也是为什么图算法的性能优化如此重要。
在剖析图算法的具体分类之前,我们先了解一个设计良好的图算法应该具备的特征。通过梳理过去一个半世纪以来多位数学家和计算机学家对于算法特征的共性探讨,我们总结了如下5点:
1)无歧义,即确定的操作逻辑。
2)清晰、明确的操作步骤。
3)具备良好的可行性(如时间、空间、复杂度与效率)。
4)定义了明确的输入、输出规则,以及可验证正确性。
5)在有限步骤内可以完成。
关于图算法的分类,业界并没有严格意义上的共识。有的侧重于学术研究的图计算框架,甚至会把广度优先搜索(BFS)或深度优先搜索(DFS)作为算法单列,尽管它们更适合作为一种图遍历模式存在。还有的如最短路径算法,在20世纪计算机发展的前30年间(20世纪40年代至70年代),最短路径算法不断推陈出新,对于计算机体系架构的发展有相当大的推动作用。图2-2示意了一种典型的在图上寻路所对应的算法分类情况。如图2-2所示,DFS算法实现的是一种随机游走式的寻路,且不关心路径是否最短。BFS算法实现的是无权重最短寻路,而Dijkstra算法则实现的是有权重最短寻路。

我们在研究图算法的分类时,一般都把图算法归类为组合数学算法的一部分,因为组合数学涉及的领域相当广泛,而图论是其中相当重要且有代表性的一部分。在组合数学中,几乎所有的著名问题,如旅行商问题、地图着色、任务分配、线性规划(过河问题)等,都与图论或离散数学相关。按照在组合数学中的图论类算法,可以简单地把算法作如下分类。
❑图路由类算法:最小生成树类算法、最短路径问题、最长路径问题、旅行商问题等。
❑网络分析与网络流算法:链接分析、网页排序算法、网络最大流问题等。
❑图搜索类算法:A*、B*、暴力搜索、回溯问题、双向搜索算法等。
❑子图类算法:强链接子图、团(Clique)、同态子图等。
❑图可视化类算法:力导向图、频谱布局、分层渲染、弧式图等。
❑其他图算法:染色类算法、拓扑排序算法、图匹配算法、最大势问题等。
我们还可以按照如下五大维度分别对图算法进行分类,每个分类下又有一些典型子类算法。
1)按设计模式分类,可分为以下6类:
❑遍历式(列举式)。在图算法以及图查询模式中,遍历式是最为常见的。像广度优先算法与深度优先算法是最常用的图遍历模式,很多现实世界的问题就是通过这些遍历模式解决的,如象棋、围棋对弈问题。下面的回溯式算法也可以看作遍历式的一种特例。
❑穷举式(暴力计算)。在海量数据集上,穷举式计算并不一定是可行的,但很多情况下带有过滤(图上剪枝)规则的穷举式计算又是必要的。例如在工商数据集中,搜索一个自然人与一个发行人(上市公司)之间的全部最短关联路径是完全可行的,即便两者之间存在成千上万条路径。❑分而治之。分而治之是算法设计中最经典的思路,把大的问题缩小,把大的数据集缩小,通过递归、并发、分布式等方法来分块处理,最后再汇总来解决全量的问题。二进制搜索、全图k邻算法等都是典型的采用分而治之的模式来解决问题的算法。
❑回溯式、回溯式算法通常用于解决约束满足问题,如各种迷宫或字谜类的益智游戏(如经典的国际象棋八皇后问题、数独问题、背包问题等)、地图着色问题、最大割问题等。因为有约束条件限定,算法在进行某种随机遍历的过程中可能会通过回退(即回溯或剪枝)来优化遍历以找到正确的结果。
❑随机化。通过随机操作的方式来求解的算法在学术界与工业界都很常见,例如蒙特卡罗类算法在连通图中计算最小割问题的Karger算法,就是通过随机删除图中的边并合并删前相连顶点的方式来实现以多项式时间复杂度(参见下文中的按复杂度分类)求解问题。
❑归约式。归约式算法通过把一个问题转换(如映射)成另一个问题,进而寻求一种更简约的解决问题的方式。例如广度优先搜索求某个(群)顶点的k跳邻居中年龄最大者(或最小,或任意可度量维度或属性)的过程中,需要对结果集进行排序(转换),然后选取最大结果值返回,这就是一种典型的先转换再求解的归约式算法。
2)按优化问题模式分类,可分为以下3类:
❑线性规划(LP)。在最优化问题求解的过程中,经常会遇到线性规划问题,如商业管理中的降本增效问题、交通能源与通信领域的最大网络流问题等。
❑动态规划(DP)。在经济学与航空工程学领域经常会遇到动态规划问题。简而言之,动态规划问题一般通过把复杂的问题以递归的方式分解为更小的问题并找到最优解来说明该问题具备最优子结构(Optimal Substructure)。例如,只要能证明贪心算法中的每一步都是最优的,就可以用它来解决具有最优子结构的问题。贪心算法通常可以被看作动态规划类算法的一个特例,最小生成树(MST)类算法就是典型的通过分解子结构来实现的贪心算法。
❑启发式算法。启发式算法是在常规方式无法找到最优解的情况下(太慢或效果太差),通过在精度、准确性、完整性、最优性等维度之间进行协调取舍,进而实现一种近似最优解的算法方案。3)按复杂度分类。可分为以下5类:
❑恒定时间。复杂度O(1)就是典型的恒定时间。比如,无论数据集大小,通过数组或向量数据结构访问任一顶点所需的时间恒定为O(1)。
连载文章,未完待续!

相关文章:

图算法系列1: 图算法的分类有哪些?(上)
大约在公元9世纪上半叶,来自中亚古国花剌子模的波斯数学家花剌子米(al-Khwarizmi)先后出版了两本对数学界有深远影响的书籍《印度数字算术》与《代数学》,前者在12世纪被翻译为拉丁文传入欧洲,十进制也因此传入欧洲,最终所形成的…...
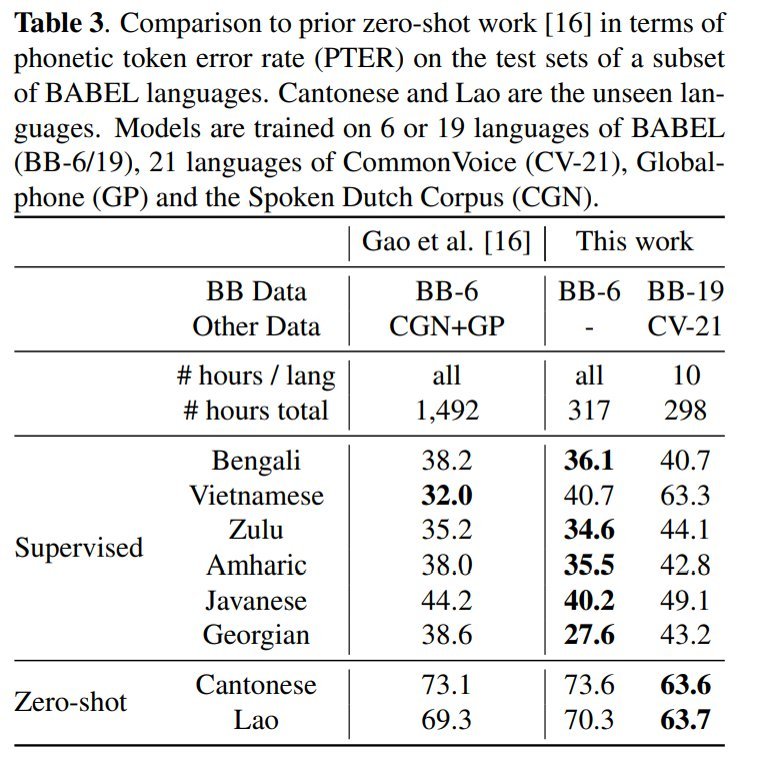
零样本学习——从多语言语料库数据中对未学习语言进行语音识别的创新技术
引言 在全球众多的语言中,只有极少数的语言在语音识别领域取得了显著的进展。这种不平衡现象的主要原因是,现有的语音识别模型往往依赖于大量的标注语音数据,而这些数据对于许多语言来说难以获得。 近年来,尽管语音识别技术取得…...

ViewStub的原理
**ViewStub是Android开发中的一个轻量级控件,主要用于懒加载布局以提高应用程序的性能和响应速度。**其原理和工作方式如下: 定义与特点 轻量级与不可见:ViewStub是一个不可见的、不占布局位置的轻量级View,它在初始化时不会实例…...

十一、Spring AOP
十一、Spring AOP 1. AOP概述2. Spring AOP快速⼊⻔2.1 引⼊AOP依赖2.2 编写AOP程序 3. Spring AOP 详解3.1 Spring AOP核⼼概念3.1.1 切点(Pointcut) Around 哪个包3.1.2 连接点(Join Point) 包下面的方法3.1.3 通知(Advice) 就是要执行的方法3.1.4 切⾯(Aspect) 3.2 通知类型…...
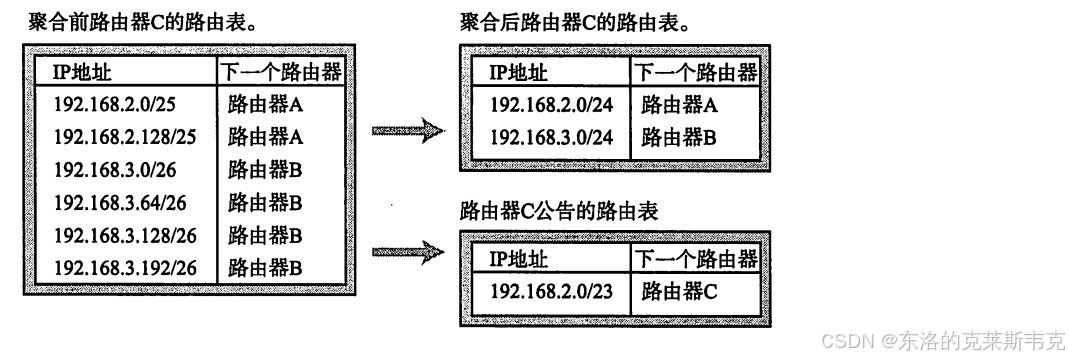
【网络】IP的路径选择——路由控制
目录 路由控制表 默认路由 主机路由 本地环回地址 路由控制表的聚合 网络分层 个人主页:东洛的克莱斯韦克-CSDN博客 路由控制表 在数据通信中,IP地址作为网络层的标识,用于指定数据包的目标位置。然而,仅有IP地址并不足以确…...
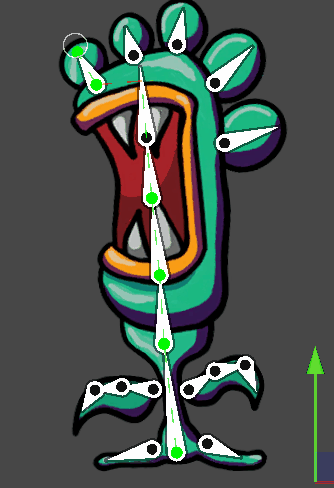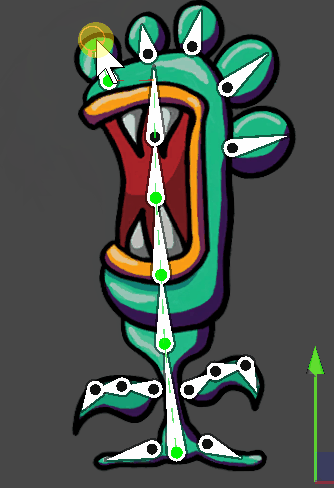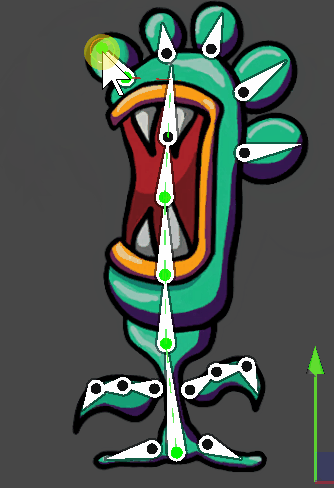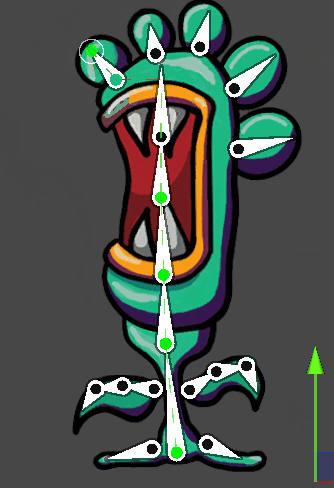
Unity动画模块 之 2D IK(反向动力学)
本文仅作笔记学习和分享,不用做任何商业用途 本文包括但不限于unity官方手册,unity唐老狮等教程知识,如有不足还请斧正 1.什么是IK 反向动力学 IK(Inverse Kinematics)是一种方法,可以根据某些子关节的最…...
关于kickstart自动安装脚本以及dhcp的设置
我将在rhel7.9内进行本次实验,需要安装并启动图形界面 hostnamectl查看是否有图形界面 没有的话 可以使用yum group list 查看,并安装server with GUI yum group install "server with GUI" -y安装完成后可以使用init 5启动 安装kickstart自…...

AWS云服务器选择最佳区域
2024年,随着全球云计算的持续发展和AWS在全球不断扩展的数据中心网络,选择合适的AWS云服务器区域成为了企业和开发者需要认真考虑的问题。九河云告诉你在做出选择之前,需要考虑以哪些关键因素: 地理位置和用户分布 选择AWS云服务…...

Unity Android端截图保存并获取展示
截屏保存方法 public static IEnumerator ScreenShot(string filePath, string fileName){yield return new WaitForEndOfFrame();Rect rect new Rect(0, 0, Screen.width, Screen.height);Texture2D screenShot new Texture2D(Screen.width, Screen.height, TextureFormat.R…...

linux高级编程——文件IO
linux高级编程——文件IO 标准IO:stdio.h 标准IO:stdio.h IO也就是输入input和输出output; I: 键盘是标准输入设备,默认输入就是指键盘 /dev/input; O: 显示器是标准输出设备,默认输…...
)
windows C++-在 C++/WinRT 中使用委托处理事件(下)
撤销已注册的委托 当你注册委托时,通常会向你返回一个令牌。 随后,可以使用该令牌撤销委托;这意味着将从事件取消注册委托,再次引发该事件时不会调用该委托。 为简单起见,上面的代码示例都没有介绍如何执行该操作。 …...

【实用工具】Stirling-PDF: 优质开源的PDF处理工具/编辑工具-含入门安装教程
文章目录 项目简介功能展示Page Operations 页面操作Conversion Operations 转换操作Security & Permissions 安全与权限Other Operations 其他业务 如何安装并使用Docker RunDocker Compose 项目简介 这是一款使用 Docker 的基于本地托管网络的强大 PDF 操作工具。它能让…...

opencv 深度图视差图可视化案例
参考:https://www.cnblogs.com/zyly/p/9373991.html(图片这里面下载的) https://blog.csdn.net/He3he3he/article/details/101053457 原理 双目摄像头 视差公式: 三角形对应推算 深度距离转换: 这里d是视差Disparity 代码 下面两种计算视差方法: import os impor…...

Golang | Leetcode Golang题解之第330题按要求补齐数组
题目: 题解: func minPatches(nums []int, n int) (patches int) {for i, x : 0, 1; x < n; {if i < len(nums) && nums[i] < x {x nums[i]i} else {x * 2patches}}return }...
第五十二天 | Bellman_ford 队列优化算法(SPFA)、BF算法判断负回路、BF之单源有限最短路(有负回路))
算法训练(leetcode)第五十二天 | Bellman_ford 队列优化算法(SPFA)、BF算法判断负回路、BF之单源有限最短路(有负回路)
刷题记录 94. 城市间货物运输 I-Bellman_ford 队列优化算法(SPFA)95. 城市间货物运输 II-BF算法判断负回路96. 城市间货物运输 III-BF之单源有限最短路(有负回路) 94. 城市间货物运输 I-Bellman_ford 队列优化算法(SPFA) 题目地址…...

SpringBoot中整合RabbitMQ(测试+部署上线 最完整)
一、RabbitMQ安装 由于在测试环境中,我们现在虚拟机上基于docker安装mq docker run \-e RABBITMQ_DEFAULT_USERquick \-e RABBITMQ_DEFAULT_PASS123 \-v mq-plugins:/plugins \--name mq \--hostname mq \-p 15672:15672 \-p 5672:5672 \--network your-net\-d \r…...

算法板子:线性DP——算出三角形中的最大路径值、求最长上升子序列、求最长公共子序列
目录 一、数字三角形——算出三角形中的最大路径值 二、最长上升子序列——求一个数组中的最长递增子序列 三、最长公共子序列——求两个字符串中的最长公共子序列 一、数字三角形——算出三角形中的最大路径值 #include <iostream> using namespace std;const int N …...

【C++】值传递
函数值传递的特点:值传递过程中即使形参改变也不会改变实参 没有返回值的函数用“ void ”定义 下面是一个实例: #include<iostream> using namespace std;//值传递 //定义函数,实现两个数字进行交换函数//如果函数不需要返回值&…...

工业三防平板助力MES系统打造工厂移动式生产管理
随着工业4.0时代的到来,智能制造、数字化车间等概念层出不穷,生产过程的可视化管理也成为了企业提升效率、优化生产的关键。而工业三防平板,凭借其坚固耐用、功能强大、便携易用等特性,成为了实现生产过程可视化管理的重要利器&am…...

keepalived+nginx实现的简单高可用故障转移
keepalived和nginx和适配 nginx服务停止后对keepalived的影响最近研究了一下keepalived绑定虚拟Ip,然后实现集群的方案,发现实现故障转移的模式,只有在keepalived服务整个挂掉后才能实现虚拟IP的漂移,和实际应用的场景不怎么适配,所以把它和nginx结合在一起实现集群高可用…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
