PHP项目任务系统小程序源码
🚀解锁高效新境界!我的项目任务系统大揭秘🔍
🌟 段落一:引言 - 为什么需要项目任务系统?
Hey小伙伴们!你是否曾为了杂乱的待办事项焦头烂额?🤯 或是项目截止日逼近,却感觉千头万绪无从下手?😫 别急,今天就来揭秘我的超级秘密武器——项目任务系统!它不仅能让你的工作生活井然有序,还能大大提升你的效率和成就感!✨
📝 段落二:构建基础 - 任务规划的艺术🎨
首先,一切从明确目标开始!🎯 把大项目拆解成一个个小任务,就像搭积木一样,每完成一块都离最终目标更近一步。记得给每个任务设定具体、可衡量的目标,比如“完成市场调研报告初稿”而非“写报告”。📝
接着,使用工具如Trello、Notion或Todoist来创建你的任务板,分类清晰,一目了然。🗂️ 把任务按照优先级排序,紧急且重要的先干,这样你就永远不会迷失方向啦!
🔧 段落三:执行秘诀 - 高效执行的法宝💼
执行时,记得采用番茄工作法或其他时间管理技巧,保持专注力爆棚!🍅 设定25分钟的高效工作时间,然后短暂休息5分钟,循环往复。这样既能保持高效,又能避免疲劳。
同时,学会委派任务也很重要!🤝 团队中每个人的强项不同,合理分配任务能让团队力量最大化。别忘了定期跟踪进度,及时调整计划,确保一切按部就班。
🌈 段落四:复盘与反馈 - 成长的加速器🚀
项目结束后,别忘了复盘!这是提升自我的绝佳机会。📊 分析哪些方法有效,哪些可以改进,总结经验教训。记得给自己一点正向反馈,庆祝每一个小成就,哪怕只是按时完成了一个看似简单的任务。🎉
🎁 段落五:结语 - 让项目任务系统成为你的日常
最后,我想说,项目任务系统不是一次性的任务清单,而是一种持续的生活习惯。🌱 通过不断的实践和调整,你会发现自己越来越能驾驭复杂的工作和项目,效率与满足感双双爆棚!
所以,小伙伴们,不妨现在就动手构建你的项目任务系统吧!让每一天都充满条理和成就感,我们一起在成长的路上越走越远!🚀👭💪
相关文章:

PHP项目任务系统小程序源码
🚀解锁高效新境界!我的项目任务系统大揭秘🔍 🌟 段落一:引言 - 为什么需要项目任务系统? Hey小伙伴们!你是否曾为了杂乱的待办事项焦头烂额?🤯 或是项目截止日逼近&…...
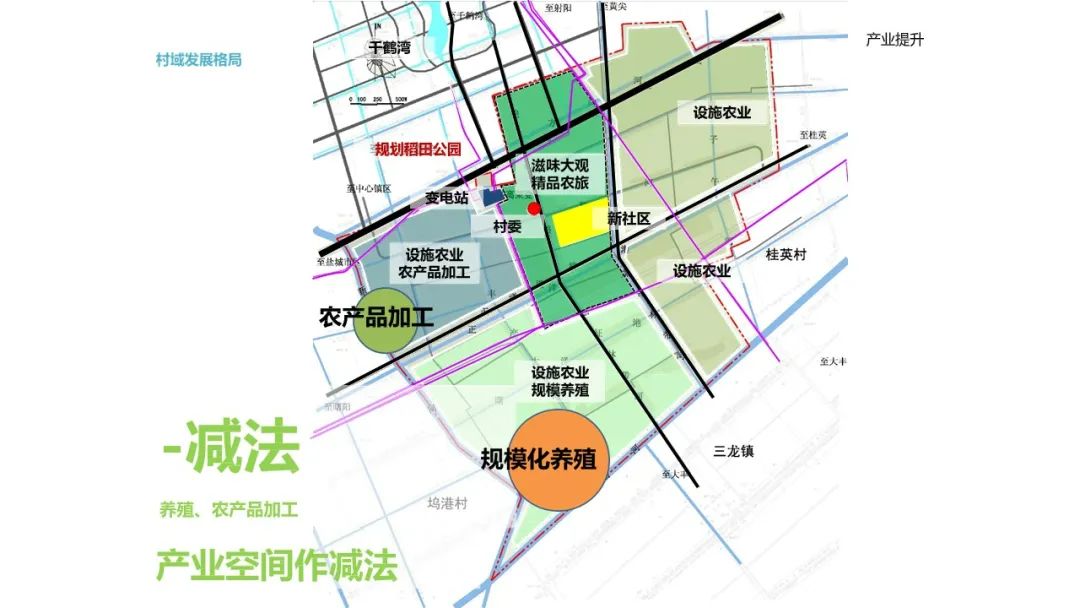
乡村振兴旅游休闲景观解决方案
乡村振兴旅游休闲景观解决方案摘要 2. 规划方案概览 规划核心:PPT展示了乡村振兴建设规划的核心区平面图及鸟瞰图,涵盖景观小品、设施农业、自行车道、新社区等设计元素。 规划策略:方案注重打造大开大合的空间感受,特色农产大观…...

【大数据】重塑时代的核心技术及其发展历程
🐇明明跟你说过:个人主页 🏅个人专栏:《大数据前沿:技术与应用并进》🏅 🔖行路有良友,便是天堂🔖 目录 一、引言 1、什么是大数据 2、大数据技术诞生的背景 二、大…...

基于python的小区监控图像拼接系统设计与实现
博主介绍: 大家好,本人精通Java、Python、C#、C、C编程语言,同时也熟练掌握微信小程序、Php和Android等技术,能够为大家提供全方位的技术支持和交流。 我有丰富的成品Java、Python、C#毕设项目经验,能够为学生提供各类…...

在HFSS中对曲线等结构进行分割(Split)
在HFSS中对曲线进行分割 我们往往需要把DXF等其他类型文件导入HFSS进行分析,但是有时需要对某一个曲线单独进行分割成两段修改。 如果是使用HFSS绘制的曲线,我们修改起来非常方便,修改参数即可。但是如果是导入的曲线,则需要使用…...

高等数学精解【8】
文章目录 直线与二元一次方程平行垂直题目点到直线距离直线束概述直线束的详细说明一、定义二、计算 三、例子例子1:中心直线束例子2:平行直线束 四、例题 参考文献 直线与二元一次方程 平行 两直线平等的条件是它们的斜率相同。 L 1 : A 1 x B 1 y …...

山石网科---WAF---巨细
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 今天被安排协助一线上架一台WAF,在这里重点总结一下WAF的内容 一.WAF部署 串联透明模式 串联模式特点: 二层透明接入,对客户网络影响小站点和webserve…...
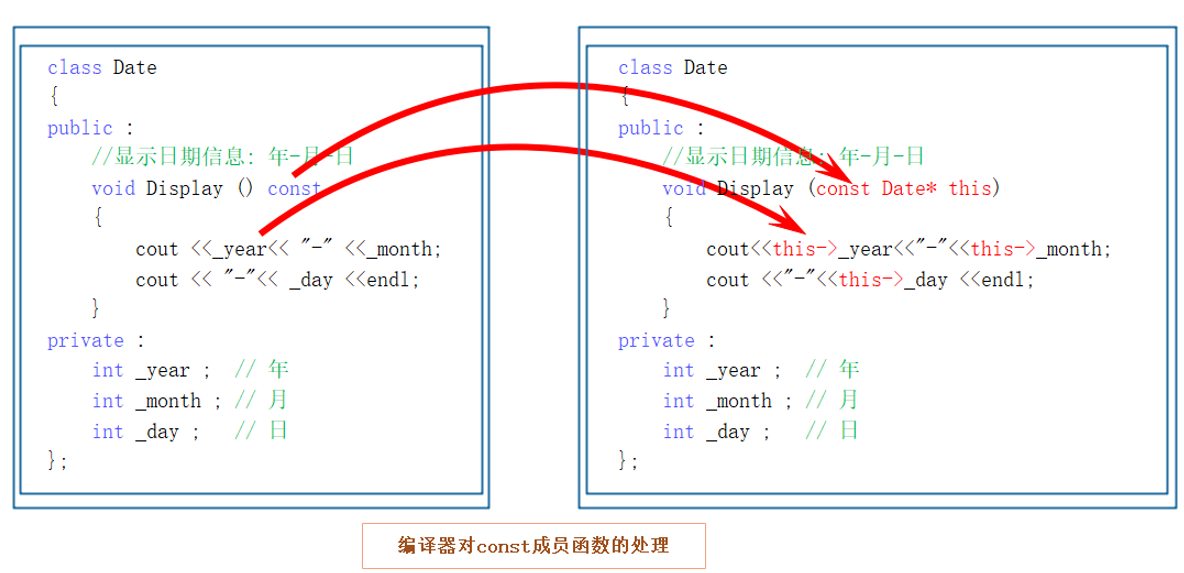
【C++】6.类和对象(4)
文章目录 5.赋值运算符重载5.1 运算符重载5.2 赋值运算符重载5.3 前置和后置重载5.4 日期类的实现 6.取地址运算符重载6.1 const成员函数6.2 取地址运算符重载 5.赋值运算符重载 5.1 运算符重载 当运算符被用于类类型的对象时,C语言允许我们通过运算符重载的形式指…...

【5.2 python中的列表】
python中的列表 Python中的列表(List)是一种非常灵活且强大的数据结构,用于存储一系列的元素。列表是可变的,意味着你可以添加、删除或修改列表中的元素。列表中的元素可以是不同类型的数据,包括整数、浮点数、字符串、…...

opencv-特征检测
1,Harris角点检测 如果粉色窗口向四周移动,窗口内的像素没有变化则认定为平坦区域,如果窗口向上移动无明显变化,而左右移动有变化则认定为边缘,如果窗口向任意方向移动均有明显变化则为角点,如下图 dst不是…...

单片机在线升级架构(bootloader+app)
1、架构(bootloaderapp) 在一定的时间内如果没有程序需要更新则自动跳转到app地址执行用户程序 内部flash 512K bootloader 跑裸机 48k 主要实现USB升级和eeprom标志位升级 app 跑freeRtos 464K 程序的基本功能,升级时软件复位开始执行bootloader升级…...

leetcode169. 多数元素,摩尔投票法附证明
leetcode169. 多数元素 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输…...

Pixel Adventure Unity2D开发完整指南
本文参考:2-2. Get and Setup Assets_哔哩哔哩_bilibili 1、下载资源 在Asset Store中下载Pix Adventure1 2的资源: 在import的时候,不用到Scene import进来,如下图所示,Scenes目录反勾选一下。 两个资源都下载完成后…...
与int main()的区别)
signed main()与int main()的区别
刷算法题时为了防止爆int ,通常会开long long #define int long long 但这样int main()会出现问题,main函数的返回值必须是signed或int,由于定义int 为long long 我们只能让返回值变为signed main() #include<bits/stdc.h> using namespace std; #define int long lo…...

【面试宝典】Java基础 这个面试题整理的不全 后期会进行补充
一、equals 和 hashcode 1、简述 hashCode() 和 equals(Object obj) 的作用及其关系 hashCode() 方法用于获取对象的哈希码,即一个整数。这个哈希码在基于哈希的集合(如HashSet、HashMap等)中用于确定对象的存储位置。 equals(Object obj)…...

获取语音文件时长
获取语音文件时长一会儿有一会儿没的,百思不得其解。 错误代码: const getAudioDuration async src > {const audio new Audio(src);const duration await new Promise(resolve > {if (audio.duration) {return resolve(parseInt(audio.duratio…...

应急响应计划:网络安全事件后的快速恢复策略
在数字化时代,网络安全威胁日益严峻,任何企业都无法完全避免遭受网络攻击或数据泄露的风险。因此,制定一套完善的应急响应计划,以便在网络安全事件发生后能够迅速、有效地进行应对和恢复,成为企业保障业务连续性、保护…...

【网络】IP和MAC地址的映射——ARP协议和ARP欺骗概述
目录 引言 ARP的工作机制 ARP欺骗 ARP欺骗的断网行为 ARP欺骗成为中间人 工具介绍 个人主页:东洛的克莱斯韦克-CSDN博客 引言 同一子网内不同主机用数据链路层的MAC地址来寻址,而不是子网内的私有IP(网络层)。数据包中的IP…...

鸿蒙(API 12 Beta3版)【音视频解封装】 文件解析封装
开发者可以调用本模块的Native API接口,完成音视频解封装,即从比特流数据中取出音频、视频等媒体帧数据。 当前支持的数据输入类型有:远程连接(http协议、HLS协议)和文件描述符(fd)。 支持的解封装格式如下: 媒体格式封装格式码…...

智能马桶盖和普通马桶盖有什么不同?
智能马桶盖与普通马桶盖之间存在显著的差异,主要体现在以下几个方面: 一、功能差异 1.清洗功能: 智能马桶盖:配备了清洗功能,包括臀洗、妇洗等,特别针对女性设计了贴心功能,如移动喷水、水流按…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
