高等数学精解【8】
文章目录
- 直线与二元一次方程
- 平行
- 垂直
- 题目
- 点到直线距离
- 直线束
- 概述
- 直线束的详细说明
- 一、定义
- 二、计算
- 三、例子
- 例子1:中心直线束
- 例子2:平行直线束
- 四、例题
- 参考文献
直线与二元一次方程
平行
- 两直线平等的条件是它们的斜率相同。
- L 1 : A 1 x + B 1 y + C 1 = 0 L 2 : A 2 x + B 2 y + C 2 = 0 k 1 = − A 1 B 1 , k 2 = − A 2 B 2 k 1 = K 2 = > L 1 / / L 2 L_1:A_1x+B_1y+C_1=0 \\L_2:A_2x+B_2y+C_2=0 \\k_1=-\frac {A_1}{B_1},k_2=-\frac {A_2}{B_2} \\k_1=K_2=>L_1//L_2 L1:A1x+B1y+C1=0L2:A2x+B2y+C2=0k1=−B1A1,k2=−B2A2k1=K2=>L1//L2
- 2 x − 9 y + 19 = 0 4 x − 18 y + 32 = 0 k 1 = − 2 − 9 = 2 9 = k 2 = − 4 − 18 = 2 9 L 1 / / L 2 2x-9y+19=0 \\4x-18y+32=0 \\k_1=- \frac 2 {-9}=\frac 2 9=k_2=-\frac 4 {-18}= \frac 2 9 \\L_1//L_2 2x−9y+19=04x−18y+32=0k1=−−92=92=k2=−−184=92L1//L2
垂直
- 垂直的条件是斜率乘积为-1
- L 1 : A 1 x + B 1 y + C 1 = 0 L 2 : A 2 x + B 2 y + C 2 = 0 k 1 = − A 1 B 1 , k 2 = − A 2 B 2 k 1 K 2 = − 1 = > L 1 ⊥ L 2 L_1:A_1x+B_1y+C_1=0 \\L_2:A_2x+B_2y+C_2=0 \\k_1=-\frac {A_1}{B_1},k_2=-\frac {A_2}{B_2} \\k_1K_2=-1=>L_1\bot L_2 L1:A1x+B1y+C1=0L2:A2x+B2y+C2=0k1=−B1A1,k2=−B2A2k1K2=−1=>L1⊥L2
- L 1 : 26 x + 6 y + 11 = 0 L 2 : 3 x − 13 y + 52 = 0 k 1 = − 26 6 = − 13 3 , k 2 = − 3 − 13 = 3 13 k 1 K 2 = − 1 = > L 1 ⊥ L 2 L_1:26x+6y+11=0 \\L_2:3x-13y+52=0 \\k_1=-\frac {26}{6}=-\frac {13}{3},k_2=-\frac {3}{-13}=\frac {3}{13} \\k_1K_2=-1=>L_1\bot L_2 L1:26x+6y+11=0L2:3x−13y+52=0k1=−626=−313,k2=−−133=133k1K2=−1=>L1⊥L2
题目
- 过点(5,3),平行于7x-9y+3=0的直线方程
7 x − 9 y + 3 = 0 , k = − 7 − 9 = 7 9 y − 3 = 7 9 ( x − 5 ) 9 y − 27 − 7 x + 35 = 0 − 7 x + 9 y + 8 = 0 7x-9y+3=0,k=-\frac 7 {-9}=\frac 7 9 \\y-3=\frac 7 9(x-5) \\9y-27-7x+35=0 \\-7x+9y+8=0 7x−9y+3=0,k=−−97=97y−3=97(x−5)9y−27−7x+35=0−7x+9y+8=0 - 过点(5,3),垂直于7x-9y+3=0的直线方程
7 x − 9 y + 3 = 0 , k = − 7 − 9 = 7 9 y − 3 = − 9 7 ( x − 5 ) 7 y − 21 + 9 x + 45 = 0 9 x + 7 y + 24 = 0 7x-9y+3=0,k=-\frac 7 {-9}=\frac 7 9 \\y-3=-\frac 9 7(x-5) \\7y-21+9x+45=0 \\9x+7y+24=0 7x−9y+3=0,k=−−97=97y−3=−79(x−5)7y−21+9x+45=09x+7y+24=0
下面内容来自文心一言
点斜式方程是直线方程的一种表示形式,它基于直线上的一点和直线的斜率来定义直线。具体来说,如果直线经过点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0),且直线的斜率为 m m m,那么这条直线的点斜式方程可以表示为:y − y 0 = m ( x − x 0 ) y - y_0 = m(x - x_0) y−y0=m(x−x0)
这里, m m m 是直线的斜率,它表示了直线倾斜的程度和方向。斜率 m m m 可以通过直线上任意两点的坐标来计算,公式为:
m = y 2 − y 1 x 2 − x 1 m = \frac{y_2 - y_1}{x_2 - x_1} m=x2−x1y2−y1
但在点斜式方程中,我们已知的是直线上的一个点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0) 和斜率 m m m,因此可以直接写出直线的方程。
点斜式方程的优点是直观且易于记忆,它直接关联了直线上的一个具体点和直线的斜率。此外,点斜式方程还可以方便地转化为其他形式的直线方程,如斜截式( y = m x + b y = mx + b y=mx+b)或一般式( A x + B y + C = 0 Ax + By + C = 0 Ax+By+C=0),以满足不同的解题需求。
需要注意的是,当直线垂直于x轴时,斜率 m m m
不存在(因为此时直线的倾斜角为90度,正切值无定义)。在这种情况下,直线方程不能表示为点斜式,而应该使用其他形式,如 x = k x = k x=k(其中
k k k 是直线与x轴交点的x坐标)。
点到直线距离
内容来自文心一言
点到直线的距离是一个重要的几何概念,它表示了从给定点到直线上所有点中最近的一个点的距离。对于直线的一般式方程 A x + B y + C = 0 Ax + By + C = 0 Ax+By+C=0 和点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0),点到直线的距离 d d d 可以用以下公式计算:d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}} d=A2+B2∣Ax0+By0+C∣
这个公式是通过点到直线的向量投影和直线的法向量来推导的。具体来说,直线的法向量是 ( A , B ) (A, B) (A,B)(因为直线方程 A x + B y + C = 0 Ax + By + C = 0 Ax+By+C=0 可以重写为 A ( x − x 1 ) + B ( y − y 1 ) = 0 A(x - x_1) + B(y - y_1) = 0 A(x−x1)+B(y−y1)=0,其中 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 是直线上的一点,但在这个公式中我们不需要它),而点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0) 到直线上任意一点 ( x , y ) (x, y) (x,y) 的向量是 ( x − x 0 , y − y 0 ) (x - x_0, y - y_0) (x−x0,y−y0)。点到直线的距离就是该向量在法向量方向上的投影的绝对值。
另外,如果直线是用点斜式 y − y 0 = m ( x − x 0 ) y - y_0 = m(x - x_0) y−y0=m(x−x0) 表示的,我们可以先将其转化为一般式 A x + B y + C = 0 Ax + By + C = 0 Ax+By+C=0(其中 A = m , B = − 1 , C = y 0 − m x 0 A = m, B = -1, C = y_0 - mx_0 A=m,B=−1,C=y0−mx0),然后再使用上面的公式来计算点到直线的距离。
需要注意的是,点到直线的距离总是非负的,因为距离是一个标量,没有方向。同时,这个公式也适用于直线与点平行(即点位于直线上)的情况,此时距离
d = 0 d = 0 d=0。
- 点(15,3)到直线7x-9y+3=0的距离
d = ∣ 7 × 15 − 9 × 3 + 3 ∣ 7 2 + ( − 9 ) 2 = 7.10 \\d=\frac {|7\times15-9\times3+3|}{\sqrt{7^2+(-9)^2}}=7.10 d=72+(−9)2∣7×15−9×3+3∣=7.10
julia> abs(7*15-9*3+3)/(sqrt(7^2+(-9)^2))
7.104169956386937
直线束
概述
- 通过某点的所有直线全体称为直线束,它们的共同点称为束的中心
- 具体来说,如果直线经过点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0),且直线的斜率为 k k k,那么这条直线的点斜式方程可以表示为:
y − y 0 = k ( x − x 0 ) y - y_0 = k(x - x_0) y−y0=k(x−x0)
将k视为参数,则可得到通过某点的所有直线,即以点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0)为中心的直线束
- 通过两条束 的直线方程得到 中心点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0),再利用点斜式方程写出直线束方程。
设直线束中的两条直线
L 1 : A 1 x + B 1 y + C 1 = 0 L 2 : A 2 x + B 2 y + C 2 = 0 直线束方程 : A 1 x + B 1 y + C 1 + λ ( A 2 x + B 2 y + C 2 ) = 0 , λ ∈ R L_1:A_1x+B_1y+C_1=0 \\L_2:A_2x+B_2y+C_2=0 \\直线束方程:A_1x+B_1y+C_1+\lambda(A_2x+B_2y+C_2)=0,\lambda \in R L1:A1x+B1y+C1=0L2:A2x+B2y+C2=0直线束方程:A1x+B1y+C1+λ(A2x+B2y+C2)=0,λ∈R - 一直线通过两相交直线 3 x − 11 y + 7 = 0 , 5 x + 7 y − 12 = 0 的交点,且垂直于直线 y = 5 x − 8 。求该直线方程 一直线通过两相交直线3x-11y+7=0,5x+7y-12=0的交点,且垂直于直线y=5x-8。求该直线方程 一直线通过两相交直线3x−11y+7=0,5x+7y−12=0的交点,且垂直于直线y=5x−8。求该直线方程
3 x − 11 y + 7 + λ ( 5 x + 7 y − 12 ) = 0 = > 3 x + 5 λ x − 11 y + 7 λ y + 7 − 12 λ = 0 = > ( 3 + 5 λ ) x + ( − 11 + 7 λ ) y + 7 − 12 λ = 0 k = − 3 + 5 λ − 11 + 7 λ = 3 + 5 λ 11 − 7 λ y = x = > k 2 = 5 , k = − 1 5 3 + 5 λ 11 − 7 λ = − 1 5 − 15 − 25 λ = 11 − 7 λ 11 + 15 + 25 λ − 7 λ = 0 26 + 18 λ = 0 λ = − 26 18 = − 13 9 ( 3 + 5 λ ) x + ( − 11 + 7 λ ) y + 7 − 12 λ = 0 = > − 38 9 x + − 190 9 y + 7 + 52 3 = 0 再化简即可 3x-11y+7+\lambda(5x+7y-12)=0 \\=>3x+5\lambda x-11y+7\lambda y+7-12\lambda=0 \\=>(3+5\lambda)x+(-11+7\lambda)y+7-12\lambda=0 \\k=-\frac{3+5\lambda}{-11+7\lambda}=\frac {3+5\lambda}{11-7\lambda} \\y=x=>k_2=5,k=-\frac 1 5 \\\frac {3+5\lambda}{11-7\lambda}=- \frac 1 5 \\-15-25\lambda=11-7\lambda \\11+15+25\lambda-7\lambda=0 \\26+18\lambda=0 \\\lambda=-\frac{26}{18}=-\frac{13}{9} \\(3+5\lambda)x+(-11+7\lambda)y+7-12\lambda=0=>- \frac {38}{9}x+- \frac{190} 9y+7+\frac {52}3=0 \\再化简即可 3x−11y+7+λ(5x+7y−12)=0=>3x+5λx−11y+7λy+7−12λ=0=>(3+5λ)x+(−11+7λ)y+7−12λ=0k=−−11+7λ3+5λ=11−7λ3+5λy=x=>k2=5,k=−5111−7λ3+5λ=−51−15−25λ=11−7λ11+15+25λ−7λ=026+18λ=0λ=−1826=−913(3+5λ)x+(−11+7λ)y+7−12λ=0=>−938x+−9190y+7+352=0再化简即可
下面内容来自文心一言
直线束的详细说明
一、定义
直线束(或直线系)是指具有某一共同性质的直线的集合。在平面几何中,直线束主要有两种类型:
- 中心直线束:指平面上通过一个固定点的所有直线的集合,此时固定点叫做束的中心,这个束本身叫做真的。
- 平行直线束:指平面上平行于一条已知直线的所有直线的集合,此时束的中心“落在无穷远处”,这个束叫做假的。
这两种直线束的定义均来源于百度百科等权威来源。
二、计算
直线束的计算通常涉及到直线方程的推导和参数的使用。
中心直线束:
- 假设已知点为(x0, y0),则通过该点的所有直线的方程可以表示为 λ 1 ( x − x 0 ) + λ 2 ( y − y 0 ) = 0 λ1(x-x0) + λ2(y-y0) = 0 λ1(x−x0)+λ2(y−y0)=0,其中λ1和λ2是不同时为零的参数。
- 如果只用一个参数k表示斜率,则方程可以简化为 y − y 0 = k ( x − x 0 ) y-y0 = k(x-x0) y−y0=k(x−x0),但注意这个方程不包含垂直于x轴的直线(即x=x0)。
平行直线束:
- 假设已知直线方程为Ax + By + C = 0,则与其平行的所有直线的方程可以表示为Ax + By + λ = 0,
其中λ是参数。直线束的计算通常涉及到线性方程的组合。
对于给定的两条直线 l 1 : A 1 x + B 1 y + C 1 = 0 l_1: A_1x + B_1y + C_1 = 0 l1:A1x+B1y+C1=0 和 l 2 : A 2 x + B 2 y + C 2 = 0 l_2: A_2x + B_2y + C_2 = 0 l2:A2x+B2y+C2=0,
含有参数 λ 1 , λ 2 \lambda_1, \lambda_2 λ1,λ2(不同时为零)的方程
λ 1 ( A 1 x + B 1 y + C 1 ) + λ 2 ( A 2 x + B 2 y + C 2 ) = 0 \lambda_1(A_1x + B_1y + C_1) + \lambda_2(A_2x + B_2y + C_2) = 0 λ1(A1x+B1y+C1)+λ2(A2x+B2y+C2)=0 表示由
l 1 l_1 l1 和 l 2 l_2 l2 决定的直线束。
- 当 l 1 l_1 l1 与 l 2 l_2 l2 相交时,该直线束是以交点为中心的直线束。
- 当 l 1 l_1 l1 与 l 2 l_2 l2 平行(但不重合)时,该直线束为平行直线束。
三、例子
例子1:中心直线束
设直线 l 1 : x + 3 y + 11 = 0 l_1: x + 3y + 11 = 0 l1:x+3y+11=0 和 l 2 : 5 x + 2 y + 6 = 0 l_2: 5x + 2y + 6 = 0 l2:5x+2y+6=0 相交于点 P P P,则过点 P P P
的所有直线的集合构成一个中心直线束。设该直线束的方程为 λ 1 ( x + 3 y + 11 ) + λ 2 ( 5 x + 2 y + 6 ) = 0 \lambda_1(x + 3y + 11) + \lambda_2(5x + 2y + 6) = 0 λ1(x+3y+11)+λ2(5x+2y+6)=0。例子2:平行直线束
设直线 l : 2 x − 3 y + 5 = 0 l: 2x - 3y + 5 = 0 l:2x−3y+5=0,则与 l l l 平行的所有直线的集合构成一个平行直线束。该直线束的方程可以表示为 2 x − 3 y + λ = 0 2x - 3y + \lambda = 0 2x−3y+λ=0,其中 λ \lambda λ 是任意实数。
四、例题
例题:求经过点 ( 2 , 3 ) (2,3) (2,3) 及两直线 x + 3 y + 11 = 0 x + 3y + 11 = 0 x+3y+11=0 和 5 x + 2 y + 6 = 0 5x + 2y + 6 = 0 5x+2y+6=0 交点的直线 L L L 的方程。
解:
- 设所求直线 L L L 的方程为 λ 1 ( x + 3 y + 11 ) + λ 2 ( 5 x + 2 y + 6 ) = 0 \lambda_1(x + 3y + 11) + \lambda_2(5x + 2y + 6) = 0 λ1(x+3y+11)+λ2(5x+2y+6)=0。
- 由于直线 L L L 过点 ( 2 , 3 ) (2,3) (2,3),代入得 2 λ 1 + 9 λ 1 + 11 λ 1 + 10 λ 2 + 6 λ 2 = 0 2\lambda_1 + 9\lambda_1 + 11\lambda_1 + 10\lambda_2 + 6\lambda_2 = 0 2λ1+9λ1+11λ1+10λ2+6λ2=0,即 21 λ 1 + 16 λ 2 = 0 21\lambda_1 + 16\lambda_2 = 0 21λ1+16λ2=0。
- 由于 λ 1 , λ 2 \lambda_1, \lambda_2 λ1,λ2 不同时为零,可以取 λ 1 = 16 , λ 2 = − 21 \lambda_1 = 16, \lambda_2 = -21 λ1=16,λ2=−21(答案不唯一,只要满足比例关系即可)。
- 因此,所求直线 L L L 的方程为 16 ( x + 3 y + 11 ) − 21 ( 5 x + 2 y + 6 ) = 0 16(x + 3y + 11) - 21(5x + 2y + 6) = 0 16(x+3y+11)−21(5x+2y+6)=0,化简得 4 x − y − 5 = 0 4x - y - 5 = 0 4x−y−5=0。
通过以上说明,我们可以清晰地理解直线束的定义、计算、例子和例题,从而更好地掌握这一重要的数学概念。
参考文献
1.《高等数学讲义》
2.文心一言
相关文章:

高等数学精解【8】
文章目录 直线与二元一次方程平行垂直题目点到直线距离直线束概述直线束的详细说明一、定义二、计算 三、例子例子1:中心直线束例子2:平行直线束 四、例题 参考文献 直线与二元一次方程 平行 两直线平等的条件是它们的斜率相同。 L 1 : A 1 x B 1 y …...

山石网科---WAF---巨细
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 今天被安排协助一线上架一台WAF,在这里重点总结一下WAF的内容 一.WAF部署 串联透明模式 串联模式特点: 二层透明接入,对客户网络影响小站点和webserve…...
【C++】6.类和对象(4)
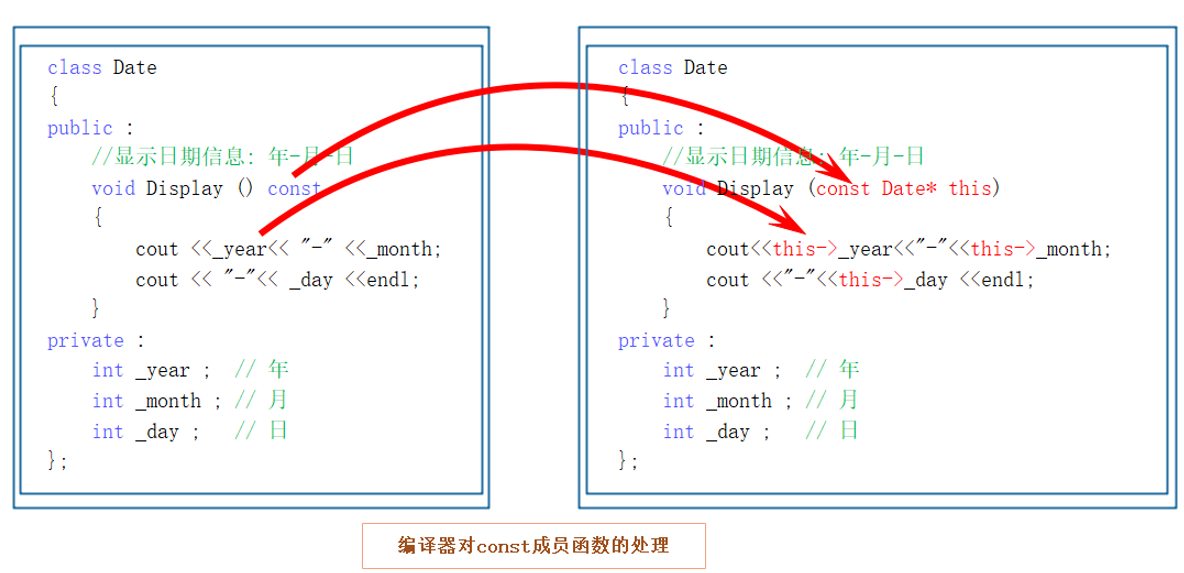
文章目录 5.赋值运算符重载5.1 运算符重载5.2 赋值运算符重载5.3 前置和后置重载5.4 日期类的实现 6.取地址运算符重载6.1 const成员函数6.2 取地址运算符重载 5.赋值运算符重载 5.1 运算符重载 当运算符被用于类类型的对象时,C语言允许我们通过运算符重载的形式指…...

【5.2 python中的列表】
python中的列表 Python中的列表(List)是一种非常灵活且强大的数据结构,用于存储一系列的元素。列表是可变的,意味着你可以添加、删除或修改列表中的元素。列表中的元素可以是不同类型的数据,包括整数、浮点数、字符串、…...

opencv-特征检测
1,Harris角点检测 如果粉色窗口向四周移动,窗口内的像素没有变化则认定为平坦区域,如果窗口向上移动无明显变化,而左右移动有变化则认定为边缘,如果窗口向任意方向移动均有明显变化则为角点,如下图 dst不是…...

单片机在线升级架构(bootloader+app)
1、架构(bootloaderapp) 在一定的时间内如果没有程序需要更新则自动跳转到app地址执行用户程序 内部flash 512K bootloader 跑裸机 48k 主要实现USB升级和eeprom标志位升级 app 跑freeRtos 464K 程序的基本功能,升级时软件复位开始执行bootloader升级…...

leetcode169. 多数元素,摩尔投票法附证明
leetcode169. 多数元素 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输…...

Pixel Adventure Unity2D开发完整指南
本文参考:2-2. Get and Setup Assets_哔哩哔哩_bilibili 1、下载资源 在Asset Store中下载Pix Adventure1 2的资源: 在import的时候,不用到Scene import进来,如下图所示,Scenes目录反勾选一下。 两个资源都下载完成后…...
与int main()的区别)
signed main()与int main()的区别
刷算法题时为了防止爆int ,通常会开long long #define int long long 但这样int main()会出现问题,main函数的返回值必须是signed或int,由于定义int 为long long 我们只能让返回值变为signed main() #include<bits/stdc.h> using namespace std; #define int long lo…...

【面试宝典】Java基础 这个面试题整理的不全 后期会进行补充
一、equals 和 hashcode 1、简述 hashCode() 和 equals(Object obj) 的作用及其关系 hashCode() 方法用于获取对象的哈希码,即一个整数。这个哈希码在基于哈希的集合(如HashSet、HashMap等)中用于确定对象的存储位置。 equals(Object obj)…...

获取语音文件时长
获取语音文件时长一会儿有一会儿没的,百思不得其解。 错误代码: const getAudioDuration async src > {const audio new Audio(src);const duration await new Promise(resolve > {if (audio.duration) {return resolve(parseInt(audio.duratio…...

应急响应计划:网络安全事件后的快速恢复策略
在数字化时代,网络安全威胁日益严峻,任何企业都无法完全避免遭受网络攻击或数据泄露的风险。因此,制定一套完善的应急响应计划,以便在网络安全事件发生后能够迅速、有效地进行应对和恢复,成为企业保障业务连续性、保护…...

【网络】IP和MAC地址的映射——ARP协议和ARP欺骗概述
目录 引言 ARP的工作机制 ARP欺骗 ARP欺骗的断网行为 ARP欺骗成为中间人 工具介绍 个人主页:东洛的克莱斯韦克-CSDN博客 引言 同一子网内不同主机用数据链路层的MAC地址来寻址,而不是子网内的私有IP(网络层)。数据包中的IP…...

鸿蒙(API 12 Beta3版)【音视频解封装】 文件解析封装
开发者可以调用本模块的Native API接口,完成音视频解封装,即从比特流数据中取出音频、视频等媒体帧数据。 当前支持的数据输入类型有:远程连接(http协议、HLS协议)和文件描述符(fd)。 支持的解封装格式如下: 媒体格式封装格式码…...

智能马桶盖和普通马桶盖有什么不同?
智能马桶盖与普通马桶盖之间存在显著的差异,主要体现在以下几个方面: 一、功能差异 1.清洗功能: 智能马桶盖:配备了清洗功能,包括臀洗、妇洗等,特别针对女性设计了贴心功能,如移动喷水、水流按…...

C# OnnxRuntime部署LivePortrait实现快速、高质量的人像驱动视频生成
目录 效果 说明 项目 模型信息 代码 下载 效果 LivePortrait实现快速、高质量的人像驱动视频生成 说明 官网地址:https://github.com/KwaiVGI/LivePortrait 代码实现参考:https://github.com/hpc203/liveportrait-onnxrun 模型下载:…...

Spring boot框架指南
1. Spring Boot 概述 1.1 定义与起源 Spring Boot是一种基于Spring框架的开源框架,旨在简化Spring应用程序的创建和开发过程。它通过提供一系列默认配置和自动配置功能,减少了开发者在配置上的工作量,使得快速搭建生产级别的Spring应用程序…...

数据结构--树与二叉树
数据结构分类 集合 线性结构(一对一) 树形结构(一对多) 图结构(多对多) 数据结构三要素 1、逻辑结构 2、数据的运算 3、存储结构(物理结构) 树的概念 树的分类 满二叉树和完全二叉树 二叉排序树 平衡二叉树 二叉树分类总结 二叉树的存储结构 …...

C#项目实战经验——计时方法总结
前言 我们在开发C#程序的过程中经常需要计算某段程序执行的时间,比如调用的某个算法的时间,这时候我们就需要利用计时工具,本文就是详细介绍在C#中我们常用哪些计时工具。 1、计时方法—StopWatch 在C#中我们可以利用Stopwatch这个类来实现…...

电子盖章软件哪个好|盖章软件
在选择电子盖章软件时,需要考虑多个因素,包括软件的功能、安全性、易用性、兼容性以及成本等。以下是根据当前市场情况推荐的一些优秀的电子盖章软件: e章宝: 功能丰富:e章宝是国内领先的电子盖章系统,功能…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
