第十四届蓝桥杯三月真题刷题训练——第 21 天
目录
第 1 题:灭鼠先锋
问题描述
运行限制
代码:
思路:
第 2 题:小蓝与钥匙
问题描述
答案提交
运行限制
代码:
思路 :
第 3 题:李白打酒加强版
第 4 题:机房
第 1 题:灭鼠先锋
问题描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
灭鼠先锋是一个老少咸宜的棋盘小游戏,由两人参与,轮流操作。
灭鼠先锋的棋盘有各种规格,本题中游戏在两行四列的棋盘上进行。游戏的规则为:两人轮流操作,每次可选择在棋盘的一个空位上放置一个棋子,或在同一行的连续两个空位上各放置一个棋子,放下棋子后使棋盘放满的一方输掉游戏。
小蓝和小乔一起玩游戏,小蓝先手,小乔后手。小蓝可以放置棋子的方法很多,通过旋转和翻转可以对应如下四种情况:
XOOO XXOO OXOO OXXO OOOO OOOO OOOO OOOO其中 O 表示棋盘上的一个方格为空,X 表示该方格已经放置了棋子。
请问,对于以上四种情况,如果小蓝和小乔都是按照对自己最优的策略来玩游戏,小蓝是否能获胜。如果获胜,请用 V 表示,否则用 L 表示。请将四种情况的胜负结果按顺序连接在一起提交。
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
代码:
package 第十四届蓝桥杯三月真题刷题训练.day21;/*** @author yx* @date 2023-03-24 8:27*/
public class 灭鼠先锋 {public static void main(String[] args) {System.out.println("LLLV");}
}
思路:
(1)因为这个题目已经把先手的四种情况进行了说明,所以就非常好想
(2)我们只需要找到一种后手下棋思路让先手必输的情况,那对于后手来说就是最优方法
(3)分别在纸上画一下下棋思路即可
第 2 题:小蓝与钥匙
问题描述
小蓝是幼儿园的老师, 他的班上有 28 个孩子, 今天他和孩子们一起进行了 一个游戏。
小蓝所在的学校是寄宿制学校, 28 个孩子分别有一个自己的房间, 每个房 间对应一把钥匙, 每把钥匙只能打开自己的门。现在小蓝让这 28 个孩子分别将 自己宿舍的钥匙上交, 再把这 28 把钥匙随机打乱分给每个孩子一把钥匙, 有 28!=28×27×⋯×1 种分配方案。小蓝想知道这些方案中, 有多少种方案恰有 一半的孩子被分到自己房间的钥匙 (即有 14 个孩子分到的是自己房间的钥匙, 有 14 个孩子分到的不是自己房间的钥匙)。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
代码:
package 第十四届蓝桥杯三月真题刷题训练.day21;/*** @author yx* @date 2023-03-24 8:51*/
public class 小蓝与钥匙 {static int N=14;public static void main(String[] args) {/*** 1、先从28个人里面选14个人给定它们的钥匙,一共有C14 28 种选法* 2、剩下的14个钥匙分别发给不同的人,使他们拿到的都不是自己的钥匙* 3、后半部分属于全错排列问题,用递推来做*//*全错排列问题:f(x)=f(x-1)+f(x-2)f(0)=0;f(1)=0;f(2)=1;*///排列组合:2006329977long C_14_28=paiLie();long f1=0;long f2=1;long temp=0;for (int i = 3; i <= 14; i++) {temp=f2;f2=(i-1)*(f1+f2);f1=temp;}System.out.println(f2*C_14_28);}//static long paiLie(){long ans=1;for (long i = 0; i < 14; i++) {ans=ans*(28-i)/(i+1);}return ans;}
}
思路 :
(1)先从28个人里面选14个人给定它们的钥匙,一共有C14 28 种选法
static long paiLie(){long ans=1;for (long i = 0; i < 14; i++) {ans=ans*(28-i)/(i+1);}return ans;}(2)剩下的14个钥匙分别发给不同的人,使他们拿到的都不是自己的钥匙,即全错排问题
(3)全错排公式:f(x)=(N-1) * [f(x-1)+f(x-2)]
(4)推导过程:
- 首先是初始值:f1=0; f2=1; f3=9这几项是可以自己手撸的
- 当i>3,很明显手撸不太行,我们静下心来分析,要找其内在的规律
- 设N个人为a,b,c,d...,N张卡为A,B,C,D...
- 若a拿b的卡B,b也拿a的卡A,则显然只剩下N-2个人拿卡,自然是f(N-2)种了(好理解)
- 若a拿b的卡B,b没拿a的卡A,则显然与N-1个人拿卡问题一样,自然是f(N-1)种了(不好理解)
- 为啥是f(N-1)种呢?注意:这里的b没拿卡A,就相当于在N个数中a没拿卡A一样的道理,在N-1个数字中,b的卡片B被a拿走了,而B又不能拿A,其实就是把卡A变相看作是卡B的平替,那是不是就相当于看作了N-1个数字进行错排
- a不一定拿B,只要是B,C,D...(N-1个)中的一个就可以了,所以在f(N-1)+f(N-2)再乘上N-1就行了.
- 得出递推公式:f(N)=(N-1)*[f(N-1)+f(N-2)]
第 3 题:李白打酒加强版
第 4 题:机房
相关文章:

第十四届蓝桥杯三月真题刷题训练——第 21 天
目录 第 1 题:灭鼠先锋 问题描述 运行限制 代码: 思路: 第 2 题:小蓝与钥匙 问题描述 答案提交 运行限制 代码: 思路 : 第 3 题:李白打酒加强版 第 4 题:机房 第 1 题࿱…...

css绘制一个Pinia小菠萝
效果如下: pinia小菠萝分为头部和身体,头部三片叶子,菠萝为身体 头部 先绘制头部的盒子,将三片叶子至于头部盒子中 先绘制中间的叶子,利用border-radius实现叶子的效果,可以借助工具来快速实现圆角的预想…...
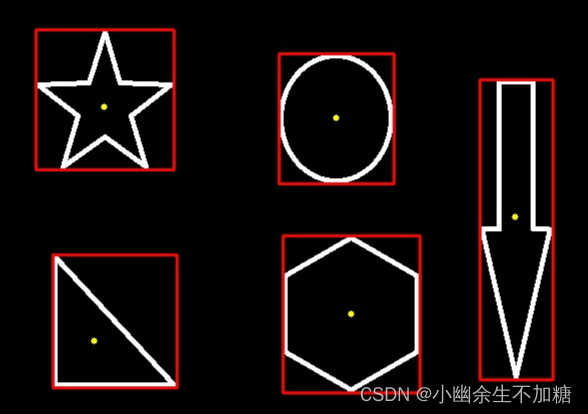
OpenCV入门(二十)快速学会OpenCV 19 对象测量
OpenCV入门(二十)快速学会OpenCV 19 对象测量1.对象测量2.多边形拟合3.计算对象中心作者:Xiou 1.对象测量 opencv 中对象测量包括: 如面积,周长,质心,边界框等。 弧长与面积测量; …...
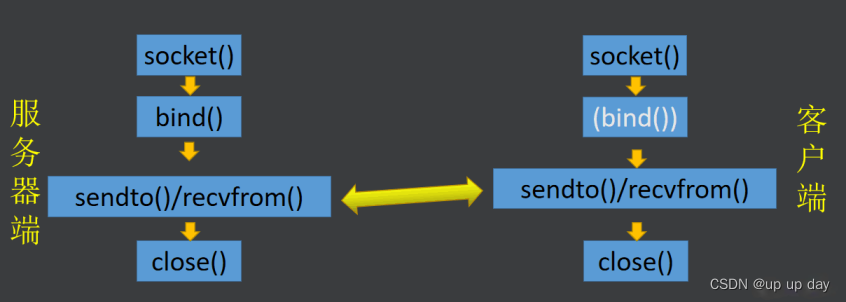
TCP和UDP协议的区别?
是否面向连接: TCP 是面向连接的传输,UDP 是面向无连接的传输。 是否是可靠传输:TCP是可靠的传输服务,在传递数据之前,会有三次握手来建立连接;在数据传递时,有确认、窗口、重传、拥塞控制机制…...
【C语言蓝桥杯每日一题】——排序
【C语言蓝桥杯每日一题】—— 排序😎前言🙌排序🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神贯注的上吧!!! 😊作者简介&am…...

学校官网的制作
学校官网 代码 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title><style>*{margin: 0;padding: 0;}.top{background-color: #3D3BB8;width: 100%;position: fixed;padding: 20px 0 12px 0;}.box{width…...

【云原生】k8s集群命令行工具kubectl之故障排除和调试命令
kubectl之故障排除和调试命令一、describe二、logs三、attach四、exec五、port-forward六、proxy七、cp八、debug8.1、案例1:共享进程空间8.2、案例2:更改启动命令、容器镜像8.3、案例3:调试节点8.4、其他一、describe 显示某个资源或某组资…...
AJAX,Axios,JSON简单了解
一. AJAX简介概念: AJAX(Asynchronous JavaScript And XML): 异步的JavaScript 和XMLAJAX作用:1.与服务器进行数据交换: 通过AJAX可以给服务器发送请求,并获取服务器响应的数据使用了AJAX和服务器进行通信,就可以使用 HTMLAJAX来替换JSP页面了2.异步交互…...

私域流量该如何打造?这套模式直接借鉴
梦龙商业案例分析,带你了解商业背后的秘密 古往今来,消费方与购买方的地位似乎就没有变过,消费者始终是处在被动接受的地位。 但到了现在,其实消费地位早已经不知不觉产生了改变。 就比如以前都是厂家有什么消费者买什么&#…...
【jenkins部署】一文弄懂自动打包部署(前后台)
这里写目录标题序言软件安装jdkmaven配置maven阿里镜像以及本地库位置git安装安装jenkins插件安装环境配置创建项目配置gitee生成gitee WebHookmaven打包验证是否打包成功连接远程服务器并重启服务远程服务器生成私钥配置ssh项目配置ssh脚本vue项目打包nodejs安装下载配置环境变…...

应届生投腾讯,被面试官问了8个和 ThreadLocal 相关的问题。
问:谈一谈ThreadLocal的结构。 ThreadLocal内部维护了一个ThreadLocalMap静态内部类,ThreadLocalMap中又维护了一个Entry静态内部类,和Entry数组。 Entry类继承弱引用类WeakReference,Entry类有一个有参构造函数,参数…...

Linux命令scp用法
本文主要讲的是scp用法如果哪里不对欢迎指出,主页https://blog.csdn.net/qq_57785602?typeblogscp 可以在win系统使用,本文百分之八十写的是win系统怎么使用,在本地上到服务器文件,从服务器下载文件到本地用工具连接到公司服务器时ÿ…...

数据质量怎么监控
目录 一、任务基线级别 二、任务级别 & 表级别 三、字段级别 1. 对指标字段的监控 2. 对维度字段的监控 四、报表级别监控 五、总结 跑了几场面试,数据质量怎么监控是经常被问到的问题,仅次于自我介绍。 因为数据行业发展了几年,数…...
.NET Core 实现Excel的导入导出
.NET Core 使用NPOI实现Excel的导入导出前言NPOI简介一、安装相对应的程序包1.1、在 “管理NuGet程序包” 中的浏览搜索:“NPOI”二、新建Excel帮助类三、调用3.1、增加一个“keywords”模型类,用作导出3.2、添加一个控制器3.3、编写导入导出的控制器代码…...

排好队,一个一个来:宫本武藏教你学队列(附各种队列源码)
文章目录前言:理解“队列”的正确姿势一个关于队列的小思考——请求处理队列的两大“护法”————顺序队列和链式队列数组实现的队列链表实现的队列循环队列关于开篇,你明白了吗?最后说一句前言: 哈喽!欢迎来到黑洞晓…...
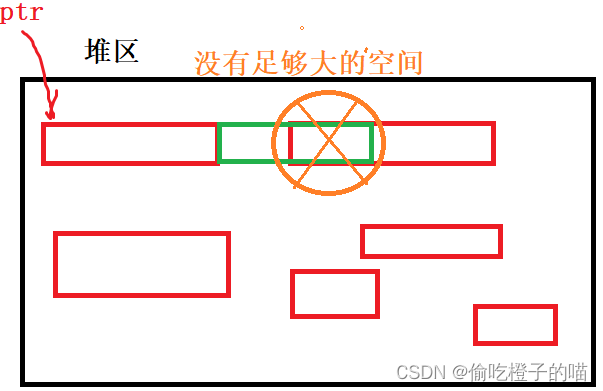
C语言--动态内存管理1
目录前言动态内存函数介绍mallocfreecallocrealloc常见的动态内存错误对NULL指针的解引用操作对动态开辟空间的越界访问对非动态开辟内存使用free释放使用free释放一块动态开辟内存的一部分对同一块动态内存多次释放动态开辟内存忘记释放(内存泄漏)对通讯…...

HTTPS 的工作原理
1、客户端发起 HTTPS 请求 这个没什么好说的,就是用户在浏览器里输入一个 https 网址,然后连接到 server 的 443 端口。 2、服务端的配置 采用 HTTPS 协议的服务器必须要有一套数字证书,可以自己制作,也可以向组织申请…...

游戏开发中建议使用半兰伯特光照
游戏开发中建议使用半兰伯特光照模型 在基本光照模型中求出漫反射部分的计算公式: 漫反射 = 入射光线的颜色和强度(c light) * 材质漫反射系数 (m diffuse)* 表面法线(n) * 其光源防线 (I) 在shader中为了不让 n和i的点乘结果为负数,即使用了saturate函数让值截取在[0,1]区…...

JavaScript到底如何存储数据?
1.var的迷幻操作 普遍的观点:JavaScript中的基本数据类型是保存在栈空间,而引用数据类型则是保存在堆空间里, 是否正确? 浏览器环境下JavaScript变量类型的运行实践结果: var a 10;console.log(a);console.log(window.a); console.log(wind…...
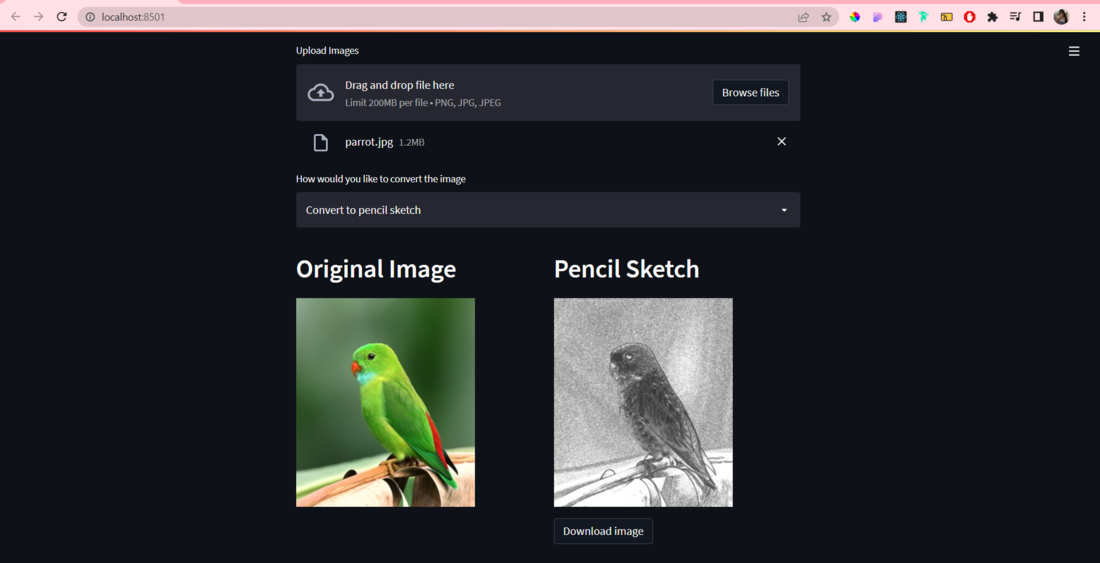
python实战应用讲解-【numpy专题篇】numpy应用案例(一)(附python示例代码)
目录 用Python分析二手车的销售价格 用Python构建GUI应用的铅笔草图 需要的包 实现步骤 完整代码 用Python分析二手车的销售价格 如今,随着技术的进步,像机器学习等技术正在许多组织中得到大规模的应用。这些模型通常与一组预定义的数据点一起工作…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
