信息学奥赛一本通1259:【例9.3】求最长不下降序列
题目:
1259:【例9.3】求最长不下降序列
时间限制: 1000 ms 内存限制: 65536 KB
提交数:51218 通过数: 20928 Special Judge
【题目描述】
设有由n(1≤n≤200)n(1≤n≤200)个不相同的整数组成的数列,记为:b(1)、b(2)、……、b(n)b(1)、b(2)、……、b(n)若存在i1<i2<i3<…<iei1<i2<i3<…<ie 且有b(i1)<=b(i2)<=…<=b(ie)b(i1)<=b(i2)<=…<=b(ie)则称为长度为e的不下降序列。程序要求,当原数列出之后,求出最长的不下降序列。
例如13,7,9,16,38,24,37,18,44,19,21,22,63,15。例中13,16,18,19,21,22,63就是一个长度为77的不下降序列,同时也有7 ,9,16,18,19,21,22,63组成的长度为88的不下降序列。
【输入】
第一行为nn,第二行为用空格隔开的nn个整数。
【输出】
第一行为输出最大个数maxmax(形式见样例);
第二行为maxmax个整数形成的不下降序列,答案可能不唯一,输出一种就可以了,本题进行特殊评测。
【输入样例】
14
13 7 9 16 38 24 37 18 44 19 21 22 63 15
【输出样例】
max=8
7 9 16 18 19 21 22 63
思路:
首先这是动规题,所以定义一个dp,dp【i】表示数组的前 i 项的最长不下降序列的长度
显然,dp[1]=1
然后我们计算 dp[2] 到 dp[n] 的值(也就是放一个从2到n的循环)
我们想一下,dp[i]是和dp[1]、dp[2]、dp[3]、dp[4]…………dp[i-1]相关的,如果我们在dp[1]、dp[2]、dp[3]、dp[4]…………dp[i-1]中找到一个最大的数(假设最大的数是dp[4])
如果a[4]<=a[i],那么dp[i]=dp[4]+1
(为什么要+1呢?因为dp【i】是一个新的数字,所以加1)
这样我们就得出了dp[i]的计算方法:
当dp【x】是 dp【1】 到 dp【i-1】 这些数中最大的数,并且a【x】<=a【i】,那么dp【i】=dp【x】+1
代码:
这是我写的,但3个样例错了
//我!的!代!码!,错!了!三!个!样!例!
//我!觉!得!是!输!出!不!下!降!序!列!的!时!候!出!问!题!了!
#include<bits/stdc++.h>
using namespace std;
long long a[210];
long long dp[210];
long long jl[210],ma=0,w;
struct aa{long long d[210],cd;
}s[210];
int main(){long long n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}dp[1]=1;//前1项的最长不下降子序列的长度为1 s[1].cd=1;s[1].d[1]=a[1];for(int i=2;i<=n;i++){long long ma=0;for(int j=1;j<=i;j++){//从1到i-1里面找答案 if(a[j]<=a[i]){//如果不下降 if(ma<dp[j]){//找个最大的数 ma=dp[j];//下一行不用看了,我输出序列的代码好像没写对 w=j; }} }dp[i]=ma+1;//下面4行不用看了,我输出序列的代码好像没写对 s[i].cd=s[w].cd+1;for(int j=1;j<s[i].cd;j++){s[i].d[j]=s[w].d[j];}s[i].d[s[i].cd]=a[i];}long long zuid=0;//zuid的意思是dp[1]到dp[n]中最大的数字 for(int i=1;i<=n;i++){if(dp[i]>zuid){zuid=dp[i];//下一行不用看了,我输出序列的代码好像没写对 w=i;}}cout<<"max="<<zuid<<endl;//下面3行不用看了,我输出序列的代码好像没写对 for(int i=1;i<=s[w].cd;i++){cout<<s[w].d[i]<<" ";}return 0;
}正确代码来自这篇文章:1259:【例9.3】求最长不下降序列_1259:【例9.3】求最长不下降序列-CSDN博客
为什么我没有改代码,而是把别人的代码拿过来呢?因!为!我!不!想!改!了 !
//这!个!代!码!才!是!对!的!
#include<bits/stdc++.h>
using namespace std;
int a[205],dp[205],pre[205];
void printff(int k){if(k == -1) return ;printff(pre[k]);cout<<a[k]<<' ';
}
int main()
{int n;cin>>n;for(int i=1;i<=n;i++) {cin>>a[i];dp[i] =1;pre[i] =-1;}int ans=-1,bk;for(int i=1;i<=n;i++){dp[i] =1;for(int j=1;j<i;j++){if(a[i] >= a[j] && dp[j] + 1 >dp[i]){dp[i] =dp[j] + 1;pre[i] = j;}}if(dp[i] > ans){ans=dp[i];bk=i;}}printf("max=%d\n",ans);printff(bk);return 0;
}
相关文章:

信息学奥赛一本通1259:【例9.3】求最长不下降序列
题目: 1259:【例9.3】求最长不下降序列 时间限制: 1000 ms 内存限制: 65536 KB 提交数:51218 通过数: 20928 Special Judge 【题目描述】 设有由n(1≤n≤200)n(1≤n≤200)个不相同的整数组成的数列,记为:b(1)、b(2)、……、…...

星露谷模组开发教程#3 事件
首发于Enaium的个人博客 SMAPI提供了一些事件,比如游戏的内容、显示、输入等事件。这些事件可以让我们在游戏中添加自己的逻辑。这一节我们就来看看如何使用这些事件。 注册一个事件 在SMAPI中,我们可以通过IModHelper的Events属性来注册事件。比如我们…...

C语言程序设计(初识C语言后部分)
愿天下无Bug,秀发常驻。 3)函数的参数 1.实际参数(实参): 真实传给函数的参数,叫实参。 实参可以是:常量、变量、表达式、函数等。 无论实参是何类型的量,在进行函数调用时&#…...

驱动基础开发
1、字符设备传统开发模板 字符设备驱动框架,首先我们需要去用module_init这个宏去修饰整个驱动的入口函数,用module_exit去修饰整个驱动的出口函数,然后还需要用MODULE_LICENSE用于声明模块的许可证类型。 在入口函数里面我们需要注册字符设…...

从苹果AppStore看AI开发者生态
从苹果 App Store 看 AI 开发者生态 在人工智能迅速发展的今天,我们不禁要问:未来的 AI 开发者生态将会是什么样子?为了回答这个问题,我们不妨回顾一下移动互联网时代最成功的开发者生态之一——苹果的 App Store。 通过分析 App …...
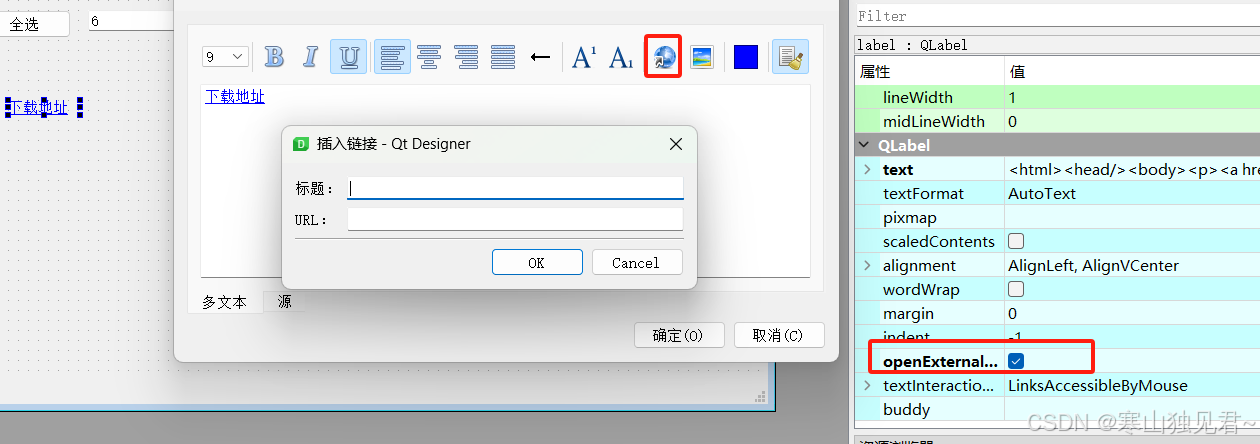
【Python学习-UI界面】PyQt5 小部件1-Label
QLabel 对象可用作显示不可编辑的文本、图像或动态GIF影片的占位符。 它还可以用作其他小部件的助记键。 标签可以显示普通文本、超链接或富文本。 1、普通文本 直接双击输入即可 2、添加超链接 选中对应Label,右键选择多信息文本,添加链接,…...
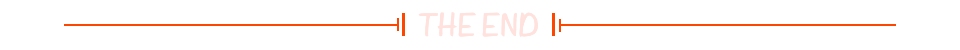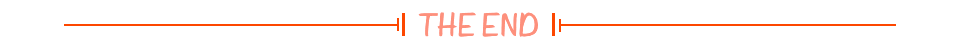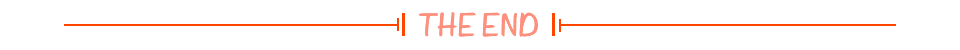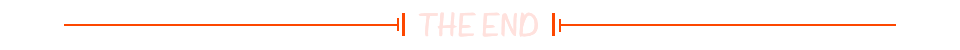
【Linux详解】进度条实现 Linux下git 的远程上传
📃个人主页:island1314 🔥个人专栏:Linux—登神长阶 ⛺️ 欢迎关注:👍点赞 👂🏽留言 😍收藏 💞 💞 💞 🚀前言 &#x…...
Android进阶之路 - res、raw、assets 资源解析、区别对比
那天遇到一个资源目录层级的问题,索性重新整理记录一下,希望能帮到如吾往昔之少年的你们,哈哈哈哈哈哈… 一脸茫然,越写越多,时间成本属实有点大,就当一起来基础扫盲吧 resdrawablemipmapvaluescolor asset…...
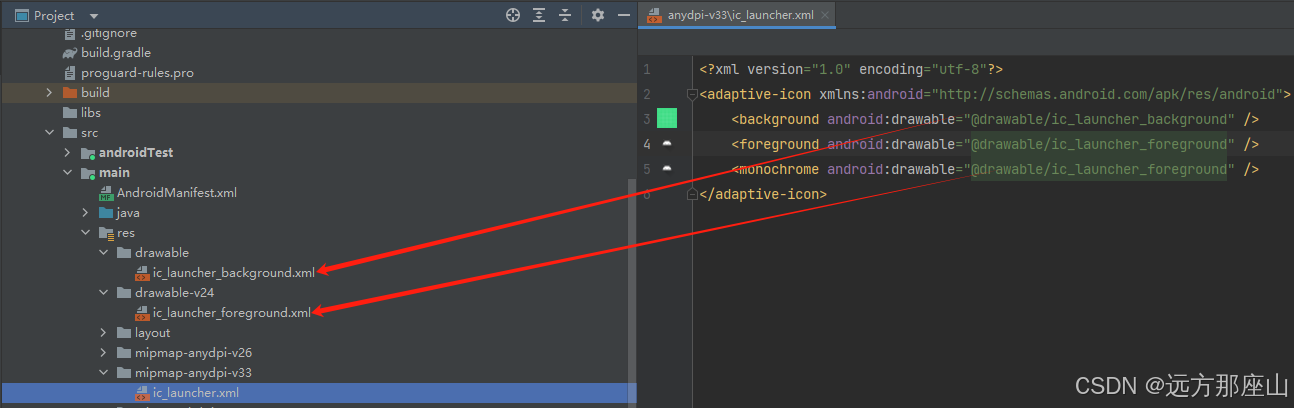
从数字化到数智化:消费零售企业如何实现门店数智化管理?
随着信息技术的飞速发展,数字化已成为企业转型的必经之路。然而,数字化本身并不是目的,而是通往数智化的桥梁。数智化,即数据智能化,是指企业通过数字化手段收集和分析数据,进而利用这些数据驱动决策和创新…...

Linux中ES的安装
文章目录 一、ES是什么1.1、ES概念介绍1.2、技术架构1.2.1、Lucene介绍 1.3、ES的工作原理1.4、ES的适用场景 二、安装前的配置2.1、创建普通用户2.2、调整文件描述符数量和虚拟内存2.3、设置shell会话的资源限制(软限制和硬限制)2.4、增加虚拟内存的设置…...
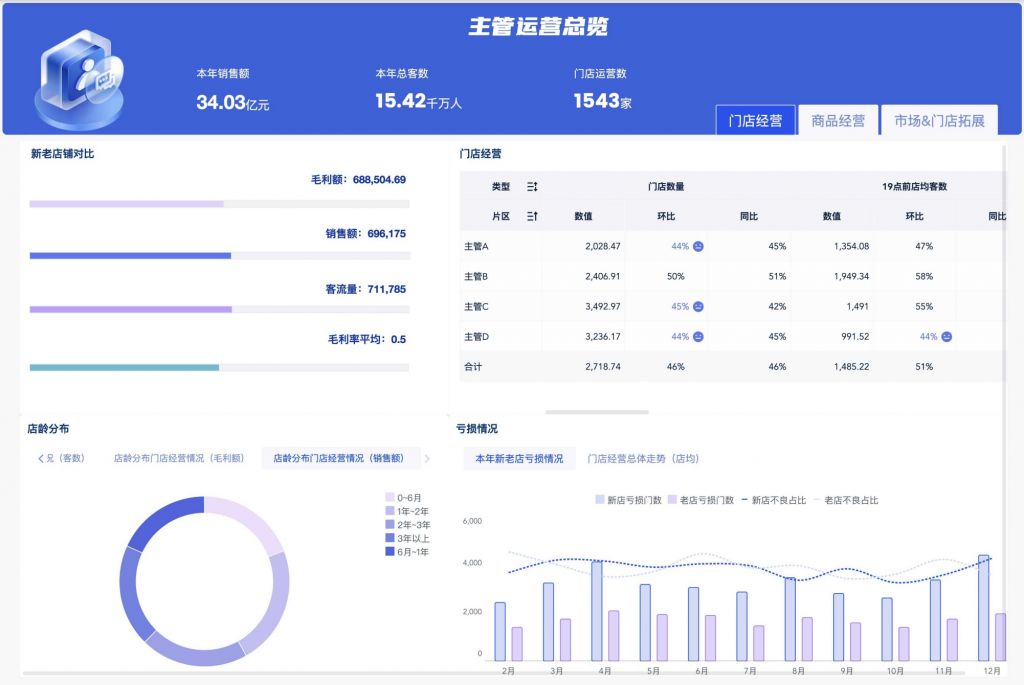
Redis远程字典服务器(5) —— hash类型详解
目录 一,hash基本情况 二,hash常用命令详解 2.1 hset,hget,hexists,hdel 2.2 hexists,hdel 2.3 hkeys,hvals 2.4 hgetall,hmget 2.5 hlen,hsetnx 2.6 hincrby&am…...
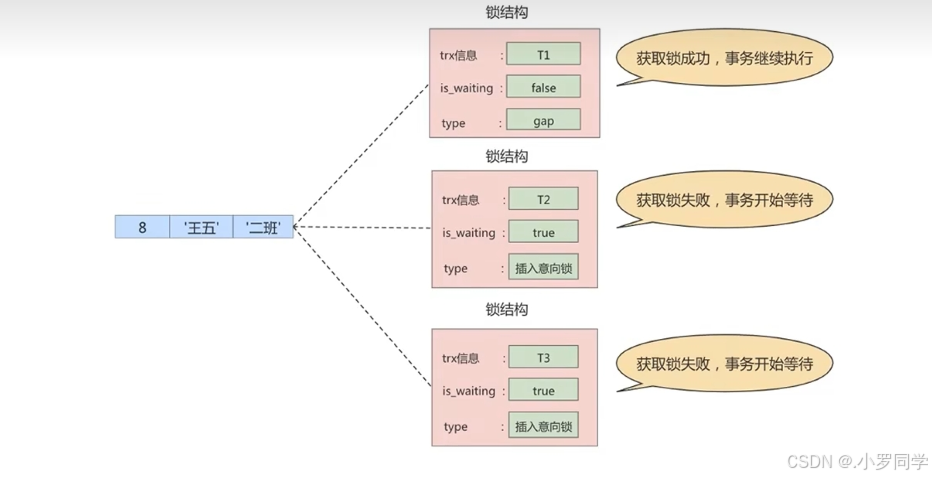
MySQL | 行锁——记录锁、间隙锁 、临键锁、插入意向锁
1、InnoDB中的行锁 行锁(Row Lock) 也称为记录锁,顾名思义,就是锁住某一行(某条记录row)。需要注意的是,MySQL服务器层并没有实现行锁机制,行级锁只在存储引擎层实现。 优点&#x…...
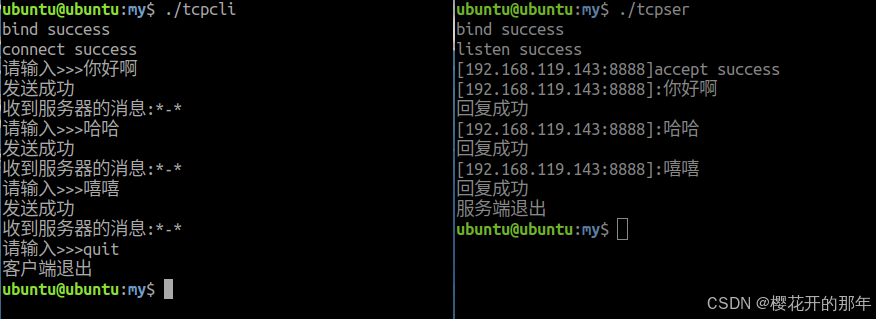
【网络编程】TCP通信基础模型实现
tcpSer.c #include <myhead.h> #define SER_IP "192.168.119.143" // 设置IP地址 #define SER_PORT 6666 // 设置端口号 int main(int argc, const char *argv[]) {// 1.创建socketint serfd socket(AF_INET, SOCK_STREAM, 0);// 参数1表示ipv4// 参数2表…...
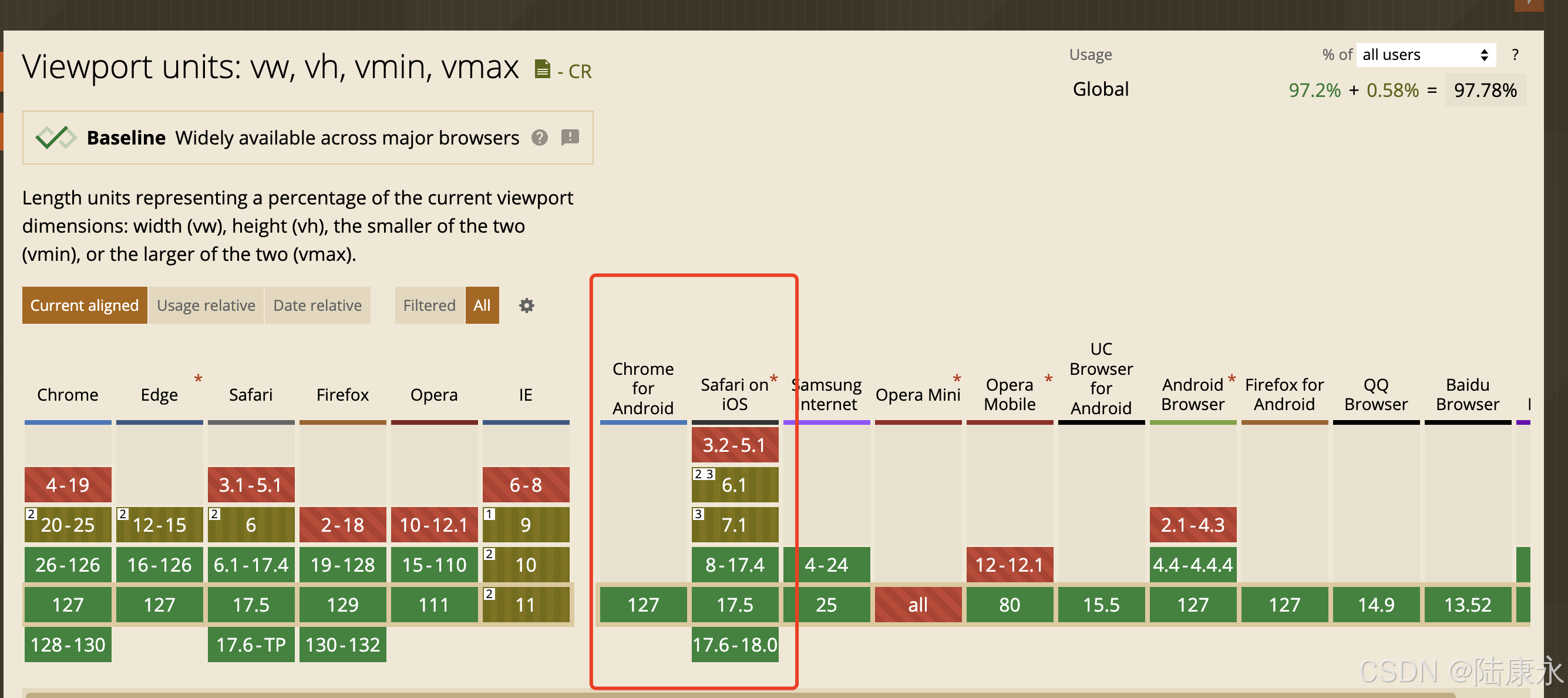
css rem之2024
话题开始前 我们都知道1rem是等于html fontSize标签的字体大小的,我们主要用来做移动端网页设计稿等比例在手机上面的显示。 看到的问题 这个html fontsize的大小是通过js动态计算的,而这个js的运行时晚于html渲染的,所以会导致一个问题&am…...

python自动化笔记:pytest框架
目录 一、pytest介绍二、测试用例命名规则2.1、pytest命名规则2.2、python命名规范 三、pytest运行方式3.1、主函数方式3.2、命令行方式3.3、通过pytest.ini的配置文件运行(常用) 四、跳过测试用例4.1 无条件跳过4.2 有条件跳过 五、用例的前后置&#x…...

wpf 路径动画 举例
先,我们需要在XAML中定义一个Path,这个Path将定义动画的路线。然后,我们将使用DoubleAnimationUsingPath来沿着这个路径移动一个元素(比如一个矩形)。 <Window x:Class"WpfApp.MainWindow" xmlns"…...

【C++】classes and object 2.8 取地址及const取地址操作符重载
这两个默认成员函数一般不用重新定义 ,编译器默认会生成。 #define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> using namespace std; class Date { public:Date* operator&(){return this;}const Date* operator&()const{return this;} privat…...

milvus helm k8s开启监控
https://milvus.io/docs/monitor.md 文章写的很清晰 ,我这边做一下个人补充,初版可能只是配置,具体的grafana 监控报表后期补一下。 架构如下: values.yaml 配置 enabled: true 改为true metrics:enabled: trueserviceMonitor:…...

牛奶饮用学习笔记
1. 常见牛奶类型 1.1 蒙牛-每日鲜语-0脂肪鲜牛奶 项目每100mL NRV%能量146kJ 能量计算 250 mL 146 kJ / 100 mL 365 kJ 250\text{mL}\times146\text{kJ}/100\text{mL} 365\text{kJ} 250mL146kJ/100mL365kJ 1.2 伊利-舒化-高钙型无乳糖牛奶 项目每100mL NRV%能量269kJ …...

php防止页面重复刷新或者重复提交
2.核心代码 显示的逻辑: //获取防止刷新的唯一标识符,start $intFlag substr(md5(time()),6); $strFlag BAOXIAOSS_.$my_user_id.$intFlag; $smarty->assign(check_is_agin_post, $strFlag); //获取防止刷新的唯一标识符,end注意:前端页面提交加入…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
