Dijkstra 算法
Dijkstra 算法( 迪杰斯特拉算法), 又叫最短路径算法, 这是常见的图论中的最短路径算法, 由 Edsger W.Dijkstra 在 1959 年发表。 这种算法能够给定一个图中的源节点( Source Node), 寻找该节点到所有其他节点的最短路径。 结合无人车路由的 lane point 场景, 算法可以这样描述:
Dijkstra 算法采用的是一种贪心的策略, 声明一个数组 dis 来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合: T, 初始时,原点 s 的路径权重被赋为 0 ( dis[s] = 0)。 若对于顶点 s 存在能直接到达的边( s,m), 则把 dis[m]设为 w( s, m) ,同时把所有其他顶点的路径长度设为无穷大。 初始时, 集合 T 只有顶点 s。
然后, 从 dis 数组选择最小值, 则该值就是源点 s 到该值对应的顶点的最短路径, 并且把该点加入到 T 中, OK, 此时完成一个顶点,
然后, 我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短, 如果是, 那么就替换这些顶点在 dis 中的值。
然后, 又从 dis 中找出最小值, 重复上述动作, 直到 T 中包含了图的所有顶点。
下面我求下图, 从顶点 v1 到其他各个顶点的最短路径。
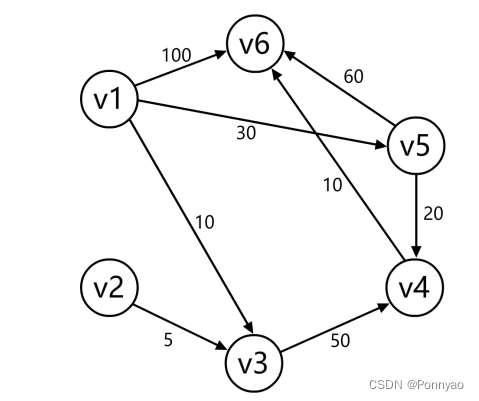
首先第一步, 我们先声明一个 dis 数组, 该数组初始化的值为:

我们的顶点集 T 的初始化为: T={v1}
既然是求 v1 顶点到其余各个顶点的最短路程, 那就先找一个离 1 号顶点最近的顶点。 通过数组 dis 可知当前离 v1 顶点最近是 v3 顶点。 当选择了 2 号顶点后, dis[2](下标从 0 开始) 的值就已经从“估计值” 变为了“确定值”,即 v1 顶点到 v3 顶点的最短路程就是当前 dis[2]值。 将 V3 加入到 T 中。
为什么呢? 因为目前离 v1 顶点最近的是 v3 顶点, 并且这个图所有的边都是正数, 那么肯定不可能通过第三个顶点中转, 使得 v1 顶点到 v3 顶点的路程进一步缩短了。 因为 v1 顶点到其它顶点的路程肯定没有 v1 到 v3 顶点短.
既然确定了一个顶点的最短路径, 下面我们就要根据这个新入的顶点 V3 会有出度, 发现以 v3 为弧尾的有: < v3,v4 >,那么我们看看路径: v1– v3– v4的长度是否比 v1– v4 短, 其实这个已经是很明显的了, 因为 dis[3]代表的就是v1– v4 的长度为无穷大, 而 v1– v3– v4 的长度为: 10+50=60, 所以更新 dis[3]的值,得到如下结果:

因此 dis[3]要更新为 60。 这个过程有个专业术语叫做“松弛”。 v1 顶点到v4 顶点的路程即 dis[3], 通过 < v3,v4> 这条边松弛成功。 这便是 Dijkstra 算法的主要思想: 通过“边” 来松弛 v1 顶点到其余各个顶点的路程。然后, 我们又从除 dis[2]和 dis[0]外的其他值中寻找最小值, 发现 dis[4]的值最小, 通过之前是解释的原理, 可以知道 v1 到 v5 的最短距离就是 dis[4]的值,
然后, 我们把 v5 加入到集合 T 中, 然后, 考虑 v5 的出度是否会影响我们的数组 dis 的值, v5 有两条出度: < v5,v4>和 < v5,v6>,然后我们发现: v1–v5– v4 的长度为: 50, 而 dis[3]的值为 60, 所以我们要更新 dis[3]的值.另外,v1-v5-v6 的长度为: 90, 而 dis[5]为 100, 所以我们需要更新 dis[5]的值。 更新后的 dis 数组如下图:

然后, 继续从 dis 中选择未确定的顶点的值中选择一个最小的值, 发现 dis[3]的值是最小的, 所以把 v4 加入到集合 T 中, 此时集合 T={v1,v3,v5,v4},然后,考虑 v4 的出度是否会影响我们的数组 dis 的值, v4 有一条出度: < v4,v6>,然后我们发现: v1– v5– v4– v6 的长度为: 60, 而 dis[5]的值为 90, 所以我们要更新 dis[5]的值, 更新后的 dis 数组如下图:

然后, 我们使用同样原理, 分别确定了 v6 和 v2 的最短路径, 最后 dis 的数组的值如下:

因此, 从图中, 我们可以发现 v1-v2 的值为: ∞, 代表没有路径从 v1 到达v2。 所以我们得到的最后的结果为:
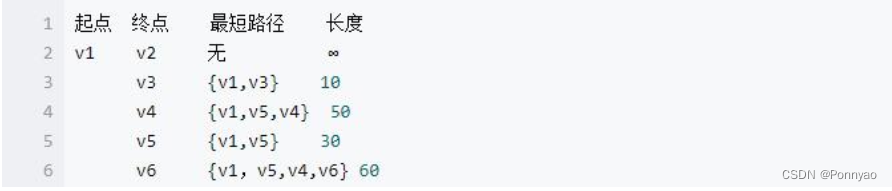
相关文章:

Dijkstra 算法
Dijkstra 算法( 迪杰斯特拉算法), 又叫最短路径算法, 这是常见的图论中的最短路径算法, 由 Edsger W.Dijkstra 在 1959 年发表。 这种算法能够给定一个图中的源节点( Source Node), …...

EIgamal 算法实现与解读
EIgamal 算法实现与解读 数学知识1.求原根2.求逆元快速幂求解EIgamal 算法1. Elgamal密钥产生2. Elgamal加密3. Elgamal解密效果如下:数学知识 1.求原根 如果g是p的原根,就是g^(p-1) = 1 (mod P)当且仅当指数为p-1的时候成立.(这里P是素数) 简单来说,g^i mod p ≠ g^j m…...

静态通讯录动态通讯录制作详解
🍕在本期的博客我们来向大家介绍一下静态通讯录的书写以及怎样将我们的静态通讯录更改为动态的模式。 🍔静态通讯录的创建 🍕就像是我们之前进行的完整程序逻辑的书写一样我们同样创建三个文件,两个 .c 文件,一个 .h 文…...
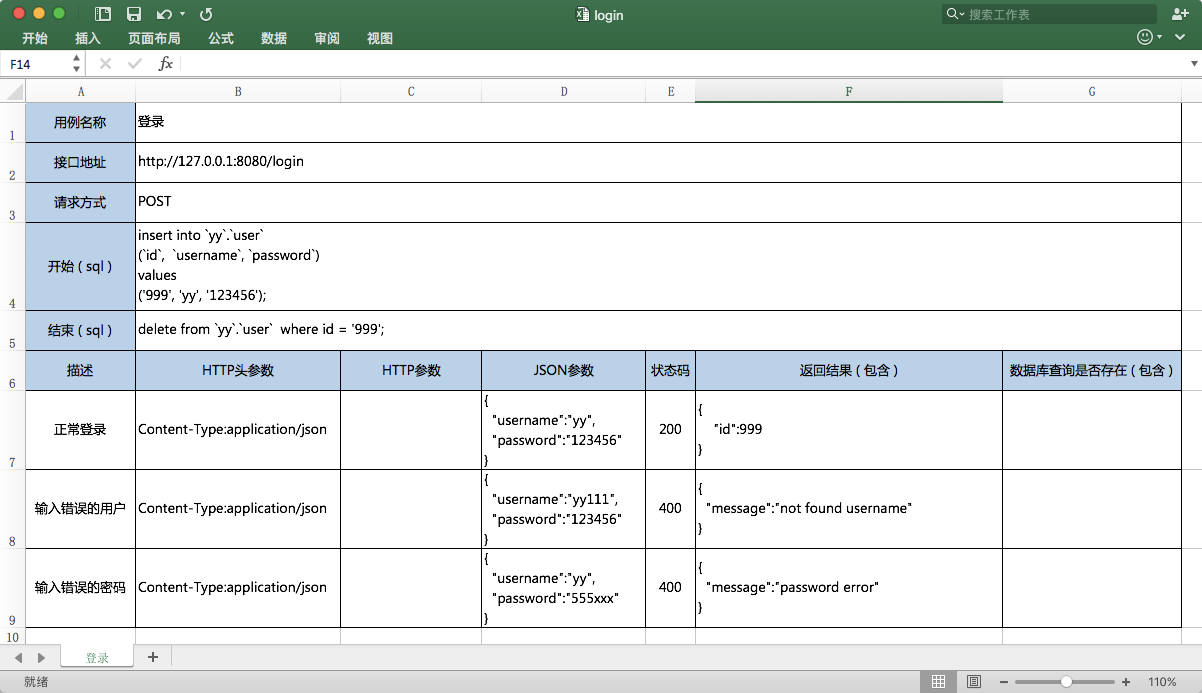
2023最新最详细【接口测试总结】
序章 说起接口测试,网上有很多例子,但是当初做为新手的我来说,看了不不知道他们说的什么,觉得接口测试,好高大上。认为学会了接口测试就能屌丝逆袭,走上人生巅峰,迎娶白富美。因此学了点开发…...
【java基础】Stream流的各种操作
文章目录基本介绍流的创建流的各种常见操作forEach方法filter方法map方法peek方法flatMap方法limit和skip方法distinct方法sorted方法收集结果收集为数组(toArray)收集为集合(collect)收集为Map关于流的一些说明(终结操…...

【Python练习】序列结构
目录 一、实验目标 二、实验内容...

CDN加速缓存的定义与作用
一、CDN的含义CDN的全称是Content Delivery Network,即内容分发网络。CDN是在原有互联网的基础上再构建虚拟分发网络,利用部署在各地的边缘节点服务器,充分发挥其负载均衡、内容分发智能调度等功能,让用户能够就地拉取数据&#x…...
Java并发高频面试题
分享50道Java并发高频面试题。 线程池 线程池:一个管理线程的池子。 为什么平时都是使用线程池创建线程,直接new一个线程不好吗? 嗯,手动创建线程有两个缺点 不受控风险频繁创建开销大 为什么不受控? 系统资源有…...
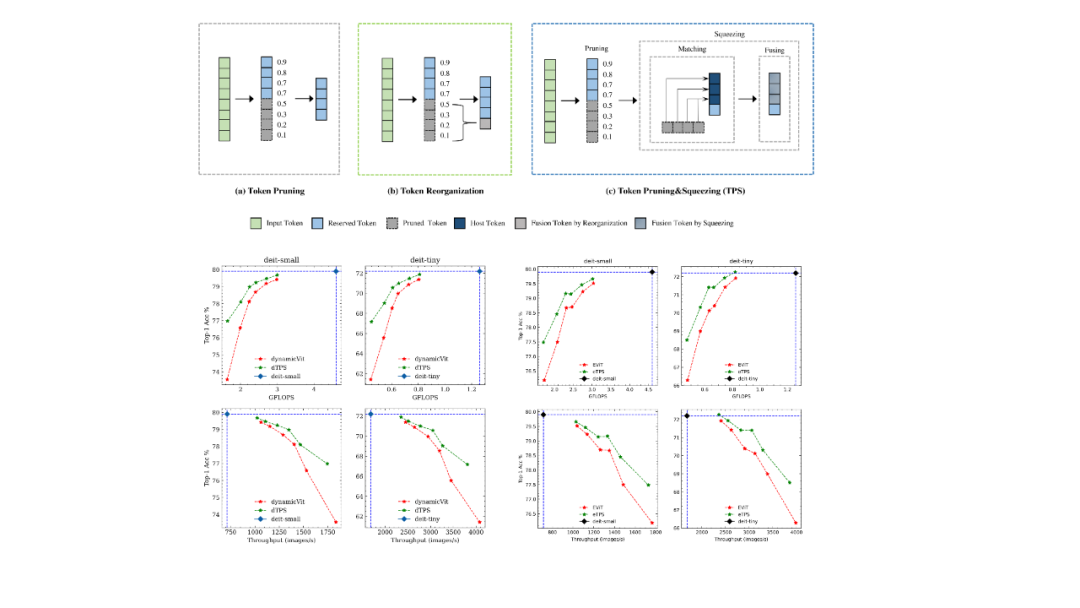
CVPR 2023 | 旷视研究院入选论文亮点解读
近日,CVPR 2023 论文接收结果出炉。近年来,CVPR 的投稿数量持续增加,今年收到有效投稿 9155 篇,和 CVPR 2022 相比增加 12%,创历史新高。最终,大会收录论文 2360 篇,接收率为 25.78 %。本次&…...
)
Vue3 学习总结补充(一)
文章目录1、Vue3中为什么修改变量的值后,视图不更新?2、使用 ref 还是 reactive?3、reactive 为什么会有响应性连接丢失情况?4、watch的不同使用方法5、watchEffect和 watch 的区别区别1:数据源的区别区别2:…...

使用ChatGPT 开放的 API 接口可以开发哪些自研工具?
使用ChatGPT开放的API接口,可以开发多种自研工具,例如: 智能聊天机器人:可以使用ChatGPT提供的语言生成能力,构建一个智能聊天机器人,能够根据用户的输入自动回复,完成自然语言交互。 文本生成工具:可以使用ChatGPT的文本生成能力,开发一个文本生成工具,例如自动生…...
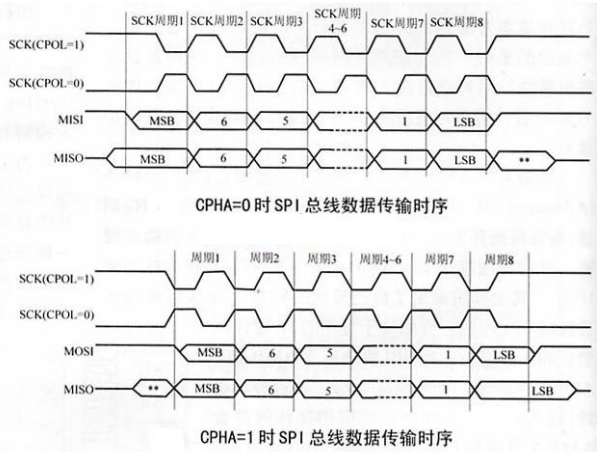
I2C和SPI总线以及通信
通讯属性 概括 Serial/parallel 串行/并行Synchronous/asynchronous 同步/异步Point-to-point / bus 点对点 总线Half-duplex/full-duplex 半双工/全双工Master-slave/ equal partners 主从/对等single-ending / differential 单端/差分 点对点和总线 点对点通讯 只有两个通…...

Spring八股文
Bean的生命周期 1.通过反射生成对象 2.填充Bean的属性 3.调用aware接口的invokeAwareMethod方法,对BeanName、BeanFactory、BeanClassLoader对象的属性设值 4.调用BeanPostProcessor的前置处理方法,其中使用较多的是ApplicationContextPostProcessor…...

20 k8sMetric 简介
一. Metric 简介metrics-server 可实现 Kubernetes 的 Resource Metrics API(metrics.k8s.io),通过此 API 可以查询 Pod 与 Node 的部分监控指标,Pod 的监控指标用于 HPA、VPA 与 kubectl top pods -n ns 命令,而 Node…...
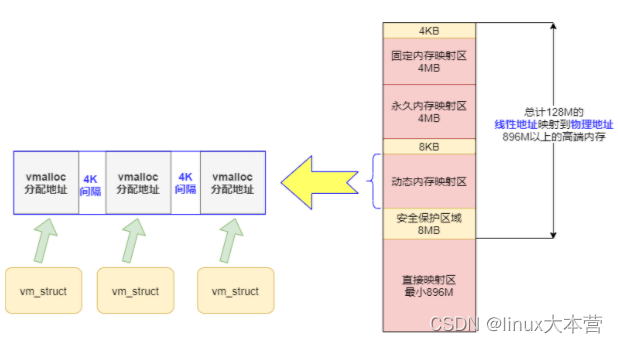
面试问了解Linux内存管理吗?10张图给你安排的明明白白
linux内存管理,内存管理好像离我们很远,但这个知识点虽然冷门(估计很多人学完根本就没机会用上)但绝对是基础中的基础,这就像武侠中的内功修炼,学完之后看不到立竿见影的效果,但对你日后的开发工…...
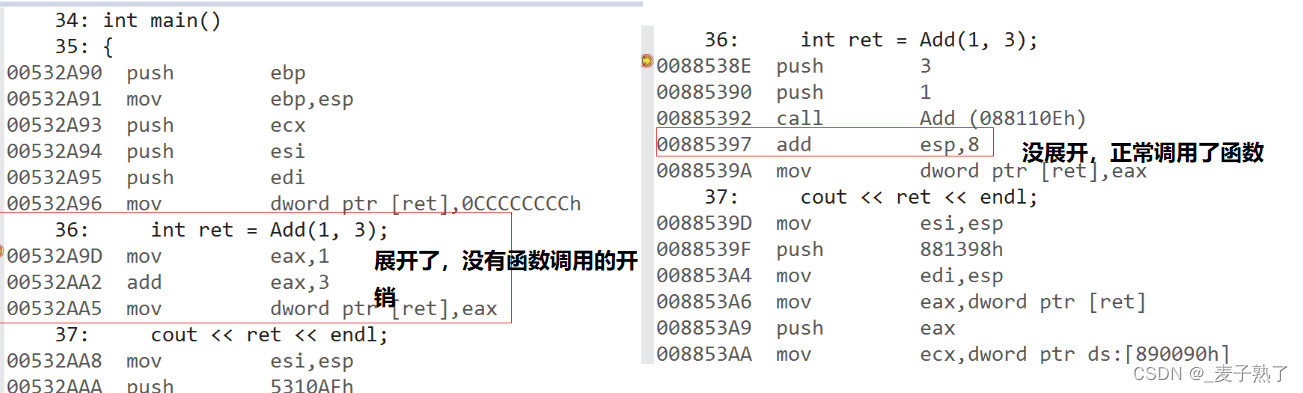
【C++】内联函数inline
文章目录概念使用特性原理概念 C中内联函数的出现解决了C语言宏函数的不足,类似于宏展开,这种在函数调用处直接嵌入函数体的函数称为内联函数,又称内嵌函数或内置函数。 以inline修饰的函数叫做内联函数,编译时C编译器会在调用内…...
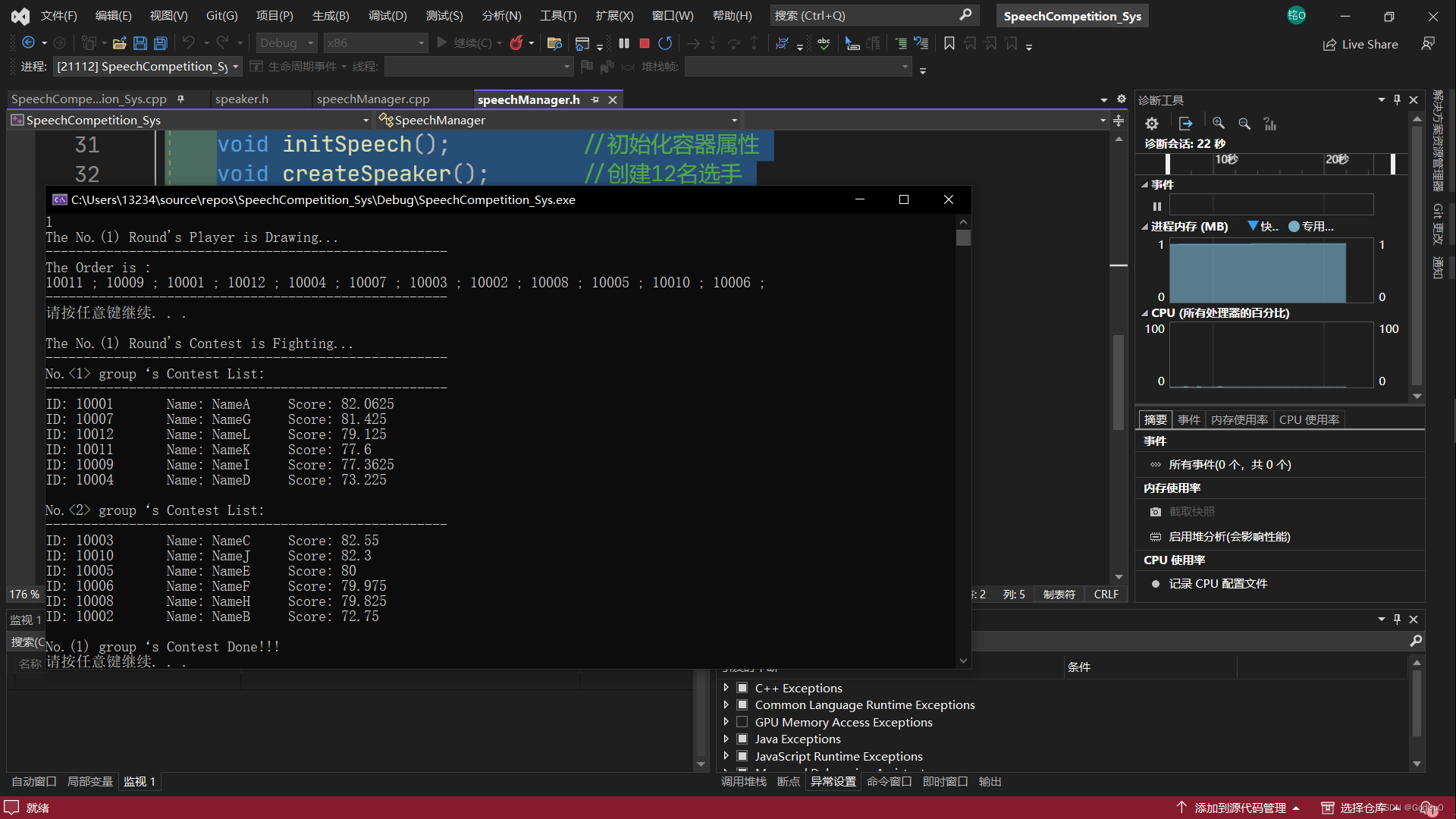
C++演讲比赛流程管理系统_黑马
任务 学校演讲比赛,12人,两轮,第一轮淘汰赛,第二轮决赛 选手编号 [ 10001 - 10012 ] 分组比赛 每组6人 10个评委 去除最高分 最低分,求平均分 为该轮成绩 每组淘汰后三名,前三名晋级决赛 决赛 前三名胜出 …...

谈谈低代码的安全问题,一文全给你解决喽
低代码是一种软件开发方法,通过使用图形化用户界面和可视化建模工具,以及自动生成代码的技术,使得开发人员可以更快速地构建和发布应用程序。 作为近些年软件开发市场热门之一,市面上也涌现了许多低代码产品,诸如简道云…...
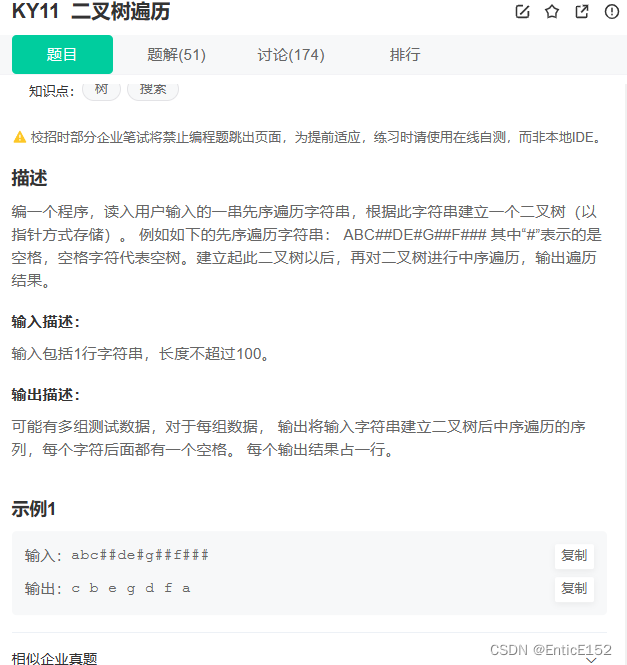
[数据结构]二叉树OJ(leetcode)
目录 二叉树OJ(leetcode)训练习题:: 1.单值二叉树 2.检查两棵树是否相同 3.二叉树的前序遍历 4.另一棵树的子树 5.二叉树的构建及遍历 6.二叉树的销毁 7.判断二叉树是否是完全二叉树 二叉树OJ(leetcode)训练习题:: 1.单值二叉…...

flutter 输入时插入分隔符
每四位插入一个分隔符import package:flutter/services.dart;class DividerInputFormatter extends TextInputFormatter {final int rear; //第一个分割位数,后面分割位,,数final String pattern; //分割符DividerInputFormatter({this.rear 4, this.pattern });overrideTex…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
