代码随想录算法训练营第43天:动态规划part10:子序列问题
300.最长递增子序列
力扣题目链接(opens new window)
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
- 输入:nums = [10,9,2,5,3,7,101,18]
- 输出:4
- 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
子序列问题分析:
dp[i]的定义
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
为什么一定表示 “以nums[i]结尾的最长递增子序” ,因为我们在 做 递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾, 要不然这个比较就没有意义了,不是尾部元素的比较那么 如何算递增呢。
状态转移方程
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。
dp[i]的初始化
每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1.
确定遍历顺序
dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来,那么遍历i一定是从前向后遍历。
j其实就是遍历0到i-1,那么是从前到后,还是从后到前遍历都无所谓,只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯 从前向后遍历。
注意**:概括来说:不连续递增子序列的跟前0-i 个状态有关,连续递增的子序列只跟前一个状态有关——这也是考虑如何构建动态规划算法的方法
- 时间复杂度: O(n^2)
- 空间复杂度: O(n)
int lengthOfLIS(int* nums, int numsSize) {int dp[numsSize];dp[0]=1;int max_ans=1;//结果不一定在最后一个位置for (int i=1;i<numsSize;i++){dp[i]=1;//为什么要初始化成1:包含自己必然是最大的子序列,尤其是涉及到fmax,不能随便初始化的for (int j=0;j<i;j++){if(nums[j]<nums[i]) dp[i]=fmax(dp[i],dp[j]+1);}printf("%d",dp[i]);max_ans=fmax(max_ans, dp[i]);}return max_ans;
}674. 最长连续递增序列
力扣题目链接(opens new window)
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
- 输入:nums = [1,3,5,4,7]
- 输出:3
- 解释:最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
- 输入:nums = [2,2,2,2,2]
- 输出:1
- 解释:最长连续递增序列是 [2], 长度为1。
可以不用动态规划直接做:贪心 o(n) o(1)复杂度
int findLengthOfLCIS(int* nums, int numsSize) {int max_ans=1;int this=1;for (int i=1;i<numsSize;i++){if(nums[i]>nums[i-1]) {this++;max_ans=fmax(this, max_ans);} else {this=1;}}return max_ans;
}感觉动规做法过于复杂:
int findLengthOfLCIS(int* nums, int numsSize) {int max_ans=1;int dp[numsSize];dp[0]=1;for (int i=1;i<numsSize;i++){dp[i]=1;if(nums[i]>nums[i-1]) dp[i]=dp[i-1]+1;max_ans=fmax(max_ans, dp[i]);}return max_ans;
}718. 最长重复子数组
力扣题目链接(opens new window)
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:
- A: [1,2,3,2,1]
- B: [3,2,1,4,7]
- 输出:3
- 解释:长度最长的公共子数组是 [3, 2, 1] 。
提示:
- 1 <= len(A), len(B) <= 1000
- 0 <= A[i], B[i] < 100
分析:
dp【i】【j】:是以i位置、j位置为结尾的匹配的情况——所以只和左上位置元素相关
之前考虑的时候,考虑成i位置、j位置以前的匹配的最大值情况,发现没有办法从上一个状态推导到这个状态——优先直接出结果,如果不能出结果,可以退而求其次,最大值的任务落在max_ans
上,优先考虑本次状态的情况
int findLength(int* nums1, int nums1Size, int* nums2, int nums2Size) {int dp[nums1Size][nums2Size];memset(dp,0, sizeof(dp));if(nums1[0]==nums2[0]) dp[0][0]=1;int max_ans=0;for (int i=1;i<nums1Size;i++){if(nums2[0]==nums1[i]) dp[i][0]=1;max_ans=fmax(max_ans, dp[i][0]);}for (int j=1;j<nums2Size;j++){if(nums1[0]==nums2[j]) dp[0][j]=1;max_ans=fmax(max_ans, dp[0][j]);}for (int i=1;i<nums1Size;i++){for (int j=1;j<nums2Size;j++){if(nums1[i]==nums2[j]) dp[i][j]=dp[i-1][j-1]+1;max_ans=fmax(max_ans, dp[i][j]);}}return max_ans;}相关文章:

代码随想录算法训练营第43天:动态规划part10:子序列问题
300.最长递增子序列 力扣题目链接(opens new window) 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2…...

传智教育引通义灵码进课堂,为技术人才教育学习提效
7 月 17 日,阿里云与传智教育在阿里巴巴云谷园区签署合作协议,双方将基于阿里云智能编程助手通义灵码在课程共建、品牌合作及产教融合等多个领域展开合作,共同推进 AI 教育及相关业务的发展,致力于培养适应未来社会需求的高素质技…...
企业信息化建设搞得好了叫系统工程,搞不好叫面子工程
2024-06-13 09:26贝格前端工场...

程序员如何平衡日常编码工作与提升式学习?
在快速变化的编程领域中,平衡日常编码工作与个人成长确实是一个重要且富有挑战性的议题。以下是我对这一问题的看法和建议: 1. 认识到平衡的重要性 首先,理解两者之间的平衡并非零和游戏,而是相辅相成的。高效的编码工作能够为个…...

Linux---文件系统和日志分析
文章目录 文件系统和日志分析inode和block概述inode包含文件的元信息用stat命令可以查看某个文件的inode信息Linux系统文件三个主要的时间属性 目录文件的结构用户通过文件名打开文件时,系统内部的过程查看inode号码的方法硬盘分区后的结构访问文件的简单流程inode的…...

MySQL 体系架构
文章目录 一. MySQL 分支与变种1. Drizzle2. MariaDB3. Percona Server 二. MySQL的替代1. Postgre SQL2. SQLite 三. MySQL 体系架构1.连接层2 Server层(SQL处理层)3. 存储引擎层1)MySQL官方存储引擎概要2)第三方引擎3࿰…...

跨站脚本攻击漏洞
1.JavaScript JavaScript 是一种脚本,一门编程语言,它可以在网页上实现复杂的功能,网页展现给你的不再是简单的静态信息,而是实时的内容更新,交互式的地图,2D/3D动画,滚动播放的视频等等。 &a…...
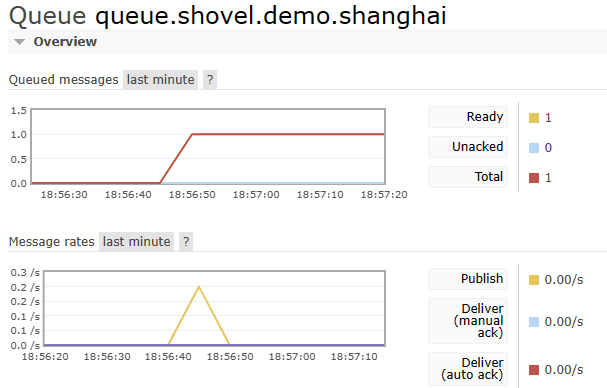
RabbitMQ入门与进阶
RabbitMQ入门与进阶 基础篇1. 为什么需要消息队列?2. 什么是消息队列?3. RabbitMQ体系结构介绍4. RabbitMQ安装5. HelloWorld6. RabbitMQ经典用法(工作模式)7. Work Queues8. Publish/Subscribe9. Routing10. Topics 进阶篇1. RabbitMQ整合SpringBoot2. 消息可靠性投递故障情…...

Unity新输入系统 之 InputActions(输入配置文件)
本文仅作笔记学习和分享,不用做任何商业用途 本文包括但不限于unity官方手册,unity唐老狮等教程知识,如有不足还请斧正 首先你应该了解新输入系统的基本单位Unity新输入系统 之 InputAction(输入配置文件最基本的单位࿰…...

Linux运维篇-误删/bin,/sbin目录怎么修复系统
这里写自定义目录标题 前言实例挂载镜像,重启系统进入救援模式拷贝镜像系统中的/bin和/sbin目录到原系统重启系统 总结 前言 当你看到这篇文章的时候,你的系统可能已经无法登录,或者正在处于登录状态但是不能执行任何常规的命令,…...

构建高效外贸电商系统的技术探索与源码开发
在当今全球化的经济浪潮中,外贸电商作为连接国内外市场的桥梁,其重要性日益凸显。一个高效、稳定、功能全面的外贸电商系统,不仅能够助力企业突破地域限制,拓宽销售渠道,还能提升客户体验,增强品牌竞争力。…...

Java设计模式:中介者模式详解与最佳实践
Java设计模式:中介者模式详解与最佳实践 1. 引言 在软件开发过程中,特别是复杂系统的构建中,模块间的交互往往成为影响代码质量的重要因素。当模块之间耦合度过高时,系统的维护、扩展和理解成本都会显著增加。为了降低模块之间的…...

Matlab绘制像素风字母颜色及透明度随机变化动画
本文是使用 Matlab 绘制像素风字母颜色及透明度随机变化动画的教程 实现效果 实现代码 如果需要更改为其他字母组合,在下面代码的基础上简单修改就可以使用。 步骤:(1) 定义字母形状;(2) 给出字母组合顺序;(3) 重新运行程序&#…...

C:每日一题:二分查找
1、知识介绍: 1.1 概念: 二分查找是一种在有序数组中查找某一特定元素的搜索算法 1.2 基本思想: 每次将待查找的范围缩小一半,通过比较中间元素与目标元素的大小,来决定是在左半部分还是右半部分继续查找。 举个生…...

python Django中使用ORM进行分组统计并降序排列
python Django中使用ORM进行分组统计并降序排列 # 使用supplier和Count进行分组统计,其中supplier为MyModel的一个字段 supplier_counts MyModel.objects.values(supplier).annotate(countCount(supplier)).order_by(-count) # 输出统计结果 for supplier_count in supplier_…...

QT C++ 编写modbus 总结
[开源库的使用]libModbus编译及使用_libmodbus库-CSDN博客 libmodbus的下载与编译_modbus库文件下载-CSDN博客 【QT5】解决 QT 界面中文显示乱码问题_qt5输出中文乱码解决方法-CSDN博客 Qt:解决qt修改完ui文件起不到作用_qt ui文件修改后不生效-CSDN博客...

基于SpringBoot的网络海鲜市场系统的设计与实现
TOC springboot219基于SpringBoot的网络海鲜市场系统的设计与实现 绪论 1.1 选题背景 当人们发现随着生产规模的不断扩大,人为计算方面才是一个巨大的短板,所以发明了各种计算设备,从结绳记事,到算筹,以及算盘&…...

c#相关基础知识
c#参数4种种别 值参:像Java的正常数据的传输 ref:对参数的指向是参数本身的地址,而不是数据的副本,所以可以对数据进行直接操作 out: 绑定控件,控件传输值赋值给类中的内部类 待定...

注意力机制 — 它是什么以及它是如何工作的
一、说明 注意力机制是深度学习领域的一个突破。它们帮助模型专注于数据的重要部分,并提高语言处理和计算机视觉等任务的理解和性能。这篇文章将深入探讨深度学习中注意力的基础知识,并展示其背后的主要思想。 二、注意力机制回顾 在我们谈论注意力之前&…...

学习嵌入式第二十六天
进程线程 1.进程的概念 2.进程 和 程序 硬盘中程序 ,加载到内存中,运行起来,就是进程 创建线程 pthread_create posix thread create 线程执行 ---体现在线程执行函数 (回调函数) 线程退出 ---pthread_exit() …...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
