从暴力递归到动态规划(2)小乖,你也在为转移方程而烦恼吗?
前引:继上篇我们讲到暴力递归的过程,这一篇blog我们将继续对从暴力递归到动态规划的实现过程,与上篇类似,我们依然采用题目的方式对其转化过程进行论述。
上篇博客:https://blog.csdn.net/m0_65431718/article/details/129604874?spm=1001.2014.3001.5502
一.n皇后问题
八皇后问题是十九世纪著名的数学家高斯于1850年提出的。问题是:在n×n的棋盘上摆放n个皇后,使任意两个皇后都不能处于同一行、同一列或同一斜线上。

我们的解题思路如下:采用暴力递归,既然要求任意两个皇后不能在同一行和同一列和同一斜线,我们依次对这三者进行讨论:①同一行:每一层递归代表一行,我们只要保证在每一层递归中只放置一个皇后即可②同一列:按照题目的要求,我们在访摆放第n层的皇后时,要保证它和前面n-1等皇后都不冲突,这就意味着我们在进行下一层递归的时候仍能有方法访问前面皇后摆放的位置:我们的第一考虑对象当然是数组,但是比较巧妙的是它是一个n*n的棋盘,第一个n代表行,第二个n代表列,我们只需要建立一个长度为n的一维数组,下标代表第几行,下标对应的数组元素代表列,作为参数带入到下一层递归中,斜线也是如此,我们详细展开说说列和斜线的要求:对于列来说,我们要遍历缓存,使前面的缓存和当前列不相等即为不冲突,对于斜线的要求来说,对于一个正方形棋盘,我们其实很容易想到的是直线的斜率为1,也就是说两个元素行的变化如果等于列的变化,我们可以说在同一条斜线上。我们根据思路给出code:
public class NEmpress {public static void main(String[] args) {//创建dateint n=4;int[]data=new int[n];System.out.println(process(data, 0, n));}//创建递归过程public static int process(int[]data,int i,int n){//判断出口条件:共有n个元素,一旦当前行越过了n-1,则说明成功if(i==n){return 1;}//循环处理每一列//如果没结束int res=0;for(int j=0;j<n;++j){//判断当前元素是否有效if(isValid(data,i,j)){data[i]=j;//进入下一层递归res+= process( data, i+1, n);}}return res;}private static boolean isValid(int[] data, int i, int j) {//在data中检验是否存在for(int k=0;k<i;++k){//第一个是判断从0到i-1行中列的元素是否相等,第二个是判断是否在同一斜线if(data[k]==j||(Math.abs(i-k)==Math.abs(j-data[k]))){return false;}}return true;}
}
如果不改变问题的实现思路,很难去实现大的效率提升,但是考虑不同的方法仍能在一定程度上提升效率(常数级提升):采用位运算,总体的实现逻辑和之前的暴力递归完全相同,但是就具体细节做出了一定的改动,我们给出递归的核心代码,并改动进行解释说明:
limit:是位数限制,对于行列数为N的棋盘,limit的限制是:对于前N个二进制位数均为1,对于N行列的棋盘而言,前N个二进制位代表棋盘的每一行(第一个二进制位代表第一行,第二个代表第二行........)
①col:对于每次摆放个皇后,就将这个二进制位置变为1,表示这个二进制位不能摆放皇后了
②leftLim:左斜线限制,如果leftLim为1,代表对于当前行来说,这个位置不能摆放皇后了。
③RightLim:右斜线限制,如果RightLim为1,同样对于当前行来说,这个位置不能摆放皇后了。
④limit==col:代表col前N个二进制位都是1,表示N个皇后都已经摆放好了,游戏结束,退出递归
⑤limit&(~(col|leftLim|rightLim)):pos是在每一行中能选择的列

⑥ mostRight=pos&(~pos+1):取出最右边的一位
⑦ pos-=mostRight:将最右边的位置从可选择的位数中去除,使当前行不能放置皇后
⑧while(pos!=0) 循环当前行中能选择的位置
⑨res+= process2(limit,col|mostRight,(leftLim|mostRight)<<1, (rightLim|mostRight)>>>1):循环下一层
public static int process2(int limit,int col,int leftLim,int rightLim){//递归出口if(limit==col){return 1;}//计算能放的位置:int pos= limit&(~(col|leftLim|rightLim));int mostRight=0;int res=0;//检验是否能递归while(pos!=0){//找最右的位置mostRight=pos&(~pos+1);pos-=mostRight;res+= process2(limit,col|mostRight,(leftLim|mostRight)<<1, (rightLim|mostRight)>>>1);}return res;我们对代码中的几个点进行解释说明:
三.机器人走路问题:(从暴力递归到动态规划的实践)
问题要求如下:
1.假设有排成一行的n个位置记为1-N,N一定大于等于2
2.开始时机器人在m位置上,m一定是1-N中的一个
3.机器人要在规定的步数到达指定的终点,计算到达指定终点的路线有多少条
4.如果机器人来到1位置只能往右来到2位置
5.如果机器人来到N位置只能往左来到N-1位置
6.如果机器人在其他位置,则机器人可以往右也可以往左

对于暴力递归,实现思路就相对比较简单:对于当前位置而言,如果位置是1,他只能选择2,如果在2-N-1的位置,他可以向左和向右走,如果在N位置,只能往N-1的位置走,不断走,直到剩余步数为0,判断是不是要求的位置,然后返回结果。
我们给出关于暴力递归的代码:
public int walking(int N,int cur,int rest,int P){//编写递归出口if(rest==0){if(cur==P){return 1;}else {return 0;}}//排除特殊情况,在0位置处:只能往后走if(cur==1){return walking(N, cur+1, rest-1, P);}//在最后一个位置,只能往前走if(cur==N){return walking(N, cur-1, rest-1, P);}//在中间,可以往前往后走return walking(N, cur-1, rest-1, P)+walking(N, cur+1, rest-1, P);}为什么说这是从暴力递归到动态规划的实践开始呢?我们对此进行解释:
我们能在暴力递归的基础上修改为动态规划,什么是动态规划呢?是将暴力递归中重复计算的过程转化为缓存,从而降低暴力递归中重复计算的次数,转而从相关缓存中获取,是一种典型的空间换时间的策略,对于动态规划而言,其实最难的部分是写出关于动态规划的转移方程。
对这道题来说,这种动态规划的类型是记忆性搜索:如果这个位置有缓存,就直接返回缓存结果,否则递归。
动态规划的的code如下:
public int walkCache(int N,int cur,int rest ,int [][]dp,int P){if(dp[cur][rest]!=-1){return dp[cur][rest];}if(rest==0){dp[cur][rest]=cur==P?1:0;return dp[cur][rest];}if(cur==1){dp[cur][rest]=walkCache(N, cur+1, rest-1, dp,P);return dp[cur][rest];}if(cur==N){dp[cur][rest]=walkCache(N, cur-1, rest-1, dp,P);return dp[cur][rest];}return dp[cur][rest]=walkCache(N, cur-1, rest-1, dp,P)+walkCache(N, cur+1, rest-1,dp, P);}}四.零和博弈问题:

问题描述:

思路:对于A而言,作为先手,他一定在纵观全局后选择对自己最有利的计划,而B作为后手,只能在A 选择之后在此基础上选择对自己最友好的计划和策略,换句话说,B选择的只能是A选择剩下的。
所以我们需要设计两个函数,一个是先手函数,选择其中相对自己而言最优的策略,即为选择自己能选的棋中的最大值,而同样需要设计一个后手函数,它的作用是:在后手参与下选择相对较小的选择(只能选择A选剩下的)
我们给出code:
package violencerecursion;/*** @author tongchen* @create 2023-03-21 16:09*/
public class GameWin {public static void main(String[] args) {GameWin gameWin = new GameWin();int[]arr={1,100,1};System.out.println(gameWin.win(arr));}public int win(int[]arr){//零和博弈问题,解题思路:先手的人拿最优的选择,后手的人只能被迫接收最差的结果int left=0;int right= arr.length-1;return Math.max(f(arr, 0, arr.length-1),s(arr, 0, arr.length-1));}private int f(int[] arr, int left, int right) {//递归出口if(left==right){return arr[left];}//选择已知策略中最优的选择return Math.max(arr[left]+s(arr,left+1,right),arr[right]+s(arr,left,right-1));}private int s(int[] arr, int left, int right) {if(right==left){return 0;}//B相当于从第二个棋子先选择(因为第一个棋子肯定被A选走了,B先手选第二个棋子)//但是这种情况下B只能选择在A纵观全局后选择最优策略之后被迫选择劣的选择(即最小值)return Math.min(f(arr, left+1, right),f(arr, left, right-1));}
}后续会更新关于动态规划的转移方程的编写思路过程,希望大家能持续关注捏~
相关文章:

从暴力递归到动态规划(2)小乖,你也在为转移方程而烦恼吗?
前引:继上篇我们讲到暴力递归的过程,这一篇blog我们将继续对从暴力递归到动态规划的实现过程,与上篇类似,我们依然采用题目的方式对其转化过程进行论述。上篇博客:https://blog.csdn.net/m0_65431718/article/details/…...

Leetcode.1638 统计只差一个字符的子串数目
题目链接 Leetcode.1638 统计只差一个字符的子串数目 Rating : 1745 题目描述 给你两个字符串 s和 t,请你找出 s中的非空子串的数目,这些子串满足替换 一个不同字符 以后,是 t串的子串。换言之,请你找到 s和 t串中 恰…...
KoTime:v2.3.9新增线程管理(线程统计、状态查询等)
功能概览 KoTime的开源版本已经迭代到了V2.3.9,目前功能如下: 实时监听方法,统计运行时长web展示方法调用链路,瓶颈可视化追踪追踪系统异常,精确定位到方法接口超时邮件通知,无需实时查看线上热更新&…...

直面风口,未来不仅是中文版ChatGPT,还有AGI大时代在等着我们
说到标题的AI2.0这个概念的研究早在2015年就研究起步了,其实大家早已知道,人工智能技术必然是未来科技发展战略中的重要一环,今天我们就从AI2.0入手,以GPT-4及文心一言的发布为切入角度,来谈一谈即将降临的AGI时代。 关…...
若依微服务(ruoyi-cloud)保姆版容器编排运行
一、简介 项目gitee地址:https://gitee.com/y_project/RuoYi-Cloud 由于该项目运行有很多坑,大家可以在git克隆拷贝到本地后,执行下面的命令使master版本回退到本篇博客的版本: git reset --hard 05ca78e82fb4e074760156359d09a…...
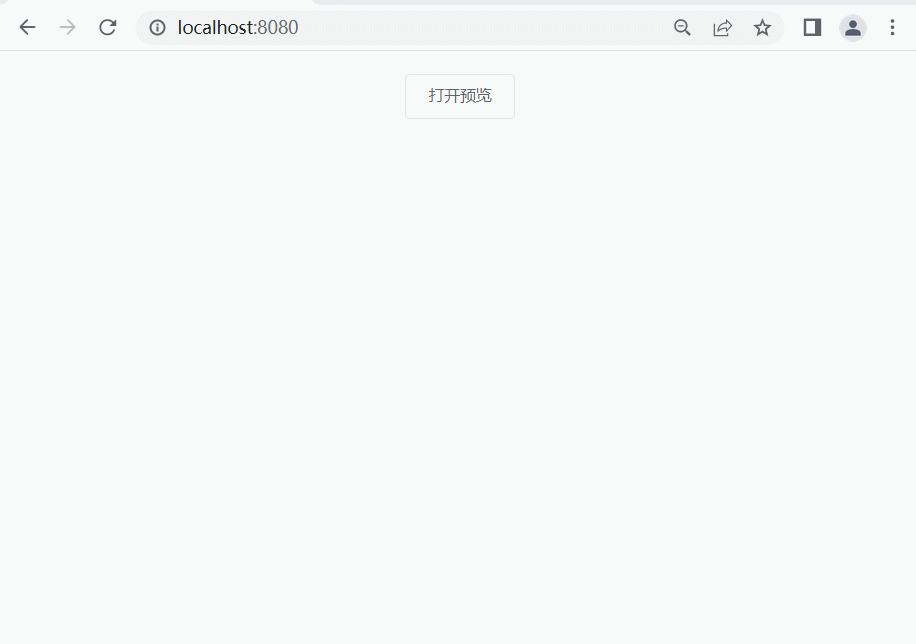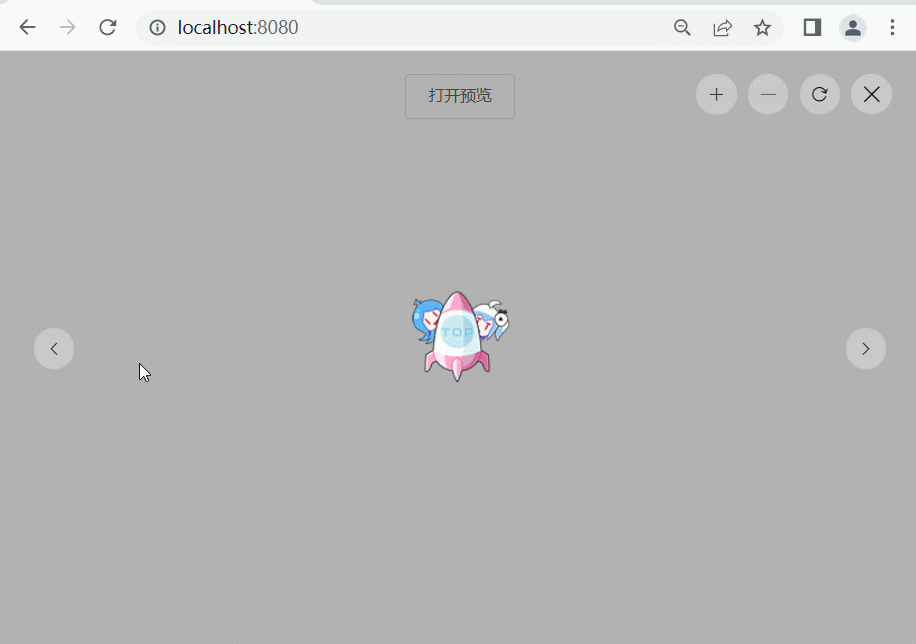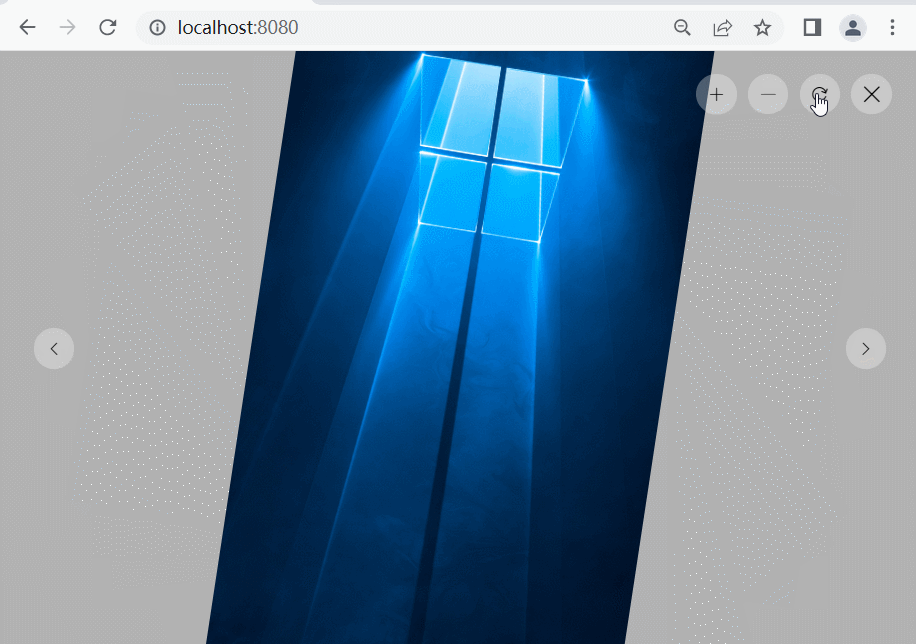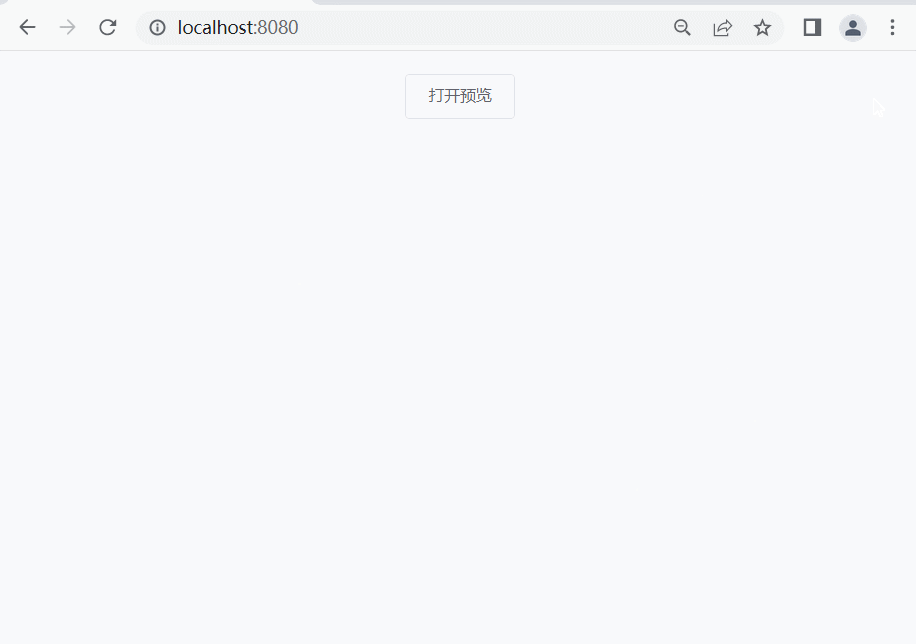
vue2图片预览插件
学习:vue插件开发实例-图片预览插件 vue2-pre-img-plugin的gitee代码 准备工作 准备图片与基础的样式 将iconfont下载的字体图标资源放在src/assets/iconfont目录下将准备预览的图片放到src/static/images目录下 PrevImg.vue 在plugins/PrevImg目录下ÿ…...

手写Promise源码的实现思路
Promise的使用: let promise new Promise((resolve, reject) > {resolve("OK");// reject("Error"); });console.log(promise);promise.then(value > {console.log("success"); }, error > {console.log("fail"…...

【数据结构】-关于树的概念和性质你了解多少??
作者:小树苗渴望变成参天大树 作者宣言:认真写好每一篇博客 作者gitee:gitee 如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点 点 关 注 吧! 树前言一、树概念及结构1.1树的概念1.2 树的相关概念1.3 树的表示1.4树在实际中的运用…...

【前端之旅】NPM必知必会
一名软件工程专业学生的前端之旅,记录自己对三件套(HTML、CSS、JavaScript)、Jquery、Ajax、Axios、Bootstrap、Node.js、Vue、小程序开发(UniApp)以及各种UI组件库、前端框架的学习。 【前端之旅】Web基础与开发工具 【前端之旅】手把手教你安装VS Code并附上超实用插件…...

Android SQLite使用事务来确保所有语句都以原子方式执行及保证数据完整性一次执行多条语句示例
execSQL 不支持用分号分隔一次执行多个 SQL 语句,虽然理论上可以实现。但是,并不建议这样做,因为这可能会导致潜在的 SQL 注入漏洞。相反,建议使用 execSQL 或 rawQuery 分别执行每个语句。 在下面的代码块中,我们正在…...
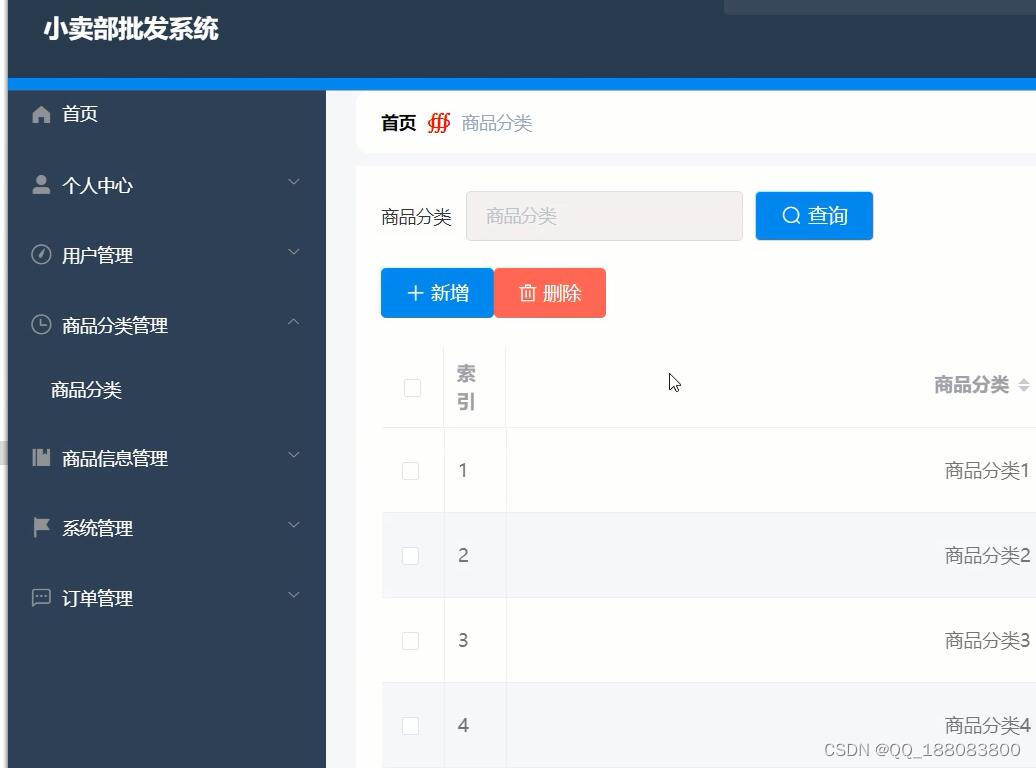
nodejs+vue校园超市小卖部零食在线购物商城系统
21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,管理工作的重要性已逐渐被人们所认识,科学化的管理,使信息存储达到…...
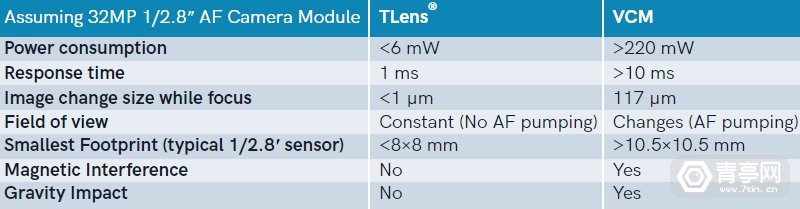
Karl Guttag:论相机对焦技术在AR/VR中的沿用
近期,AR/VR光学专家Karl Guttag介绍了两家在CES 2023展出光学传感技术的公司:poLight和CML(剑桥机电一体化)。同时介绍两家公司的原因,是因为他们提供了实现AR/VR“光学微动”(Optics Micromovement&…...
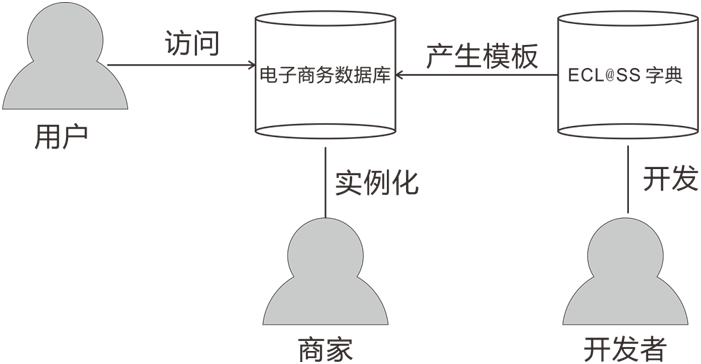
ECL@SS学习笔记(3)-概念数据模型
ECLSS 是产品,服务的分类和描述系统。本文介绍其内部的数据模型。ECLSS的作用ECLSS 标准的目标是为了实现工业界数据交换的标准化。这个标准主要作用是产品的分类和描述。分类为了有效地物料管理,供应链管理和电子商务,需要对物料进行分类和编…...

206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:head [1,2] 输出:[2,1] 示例 3: 输…...
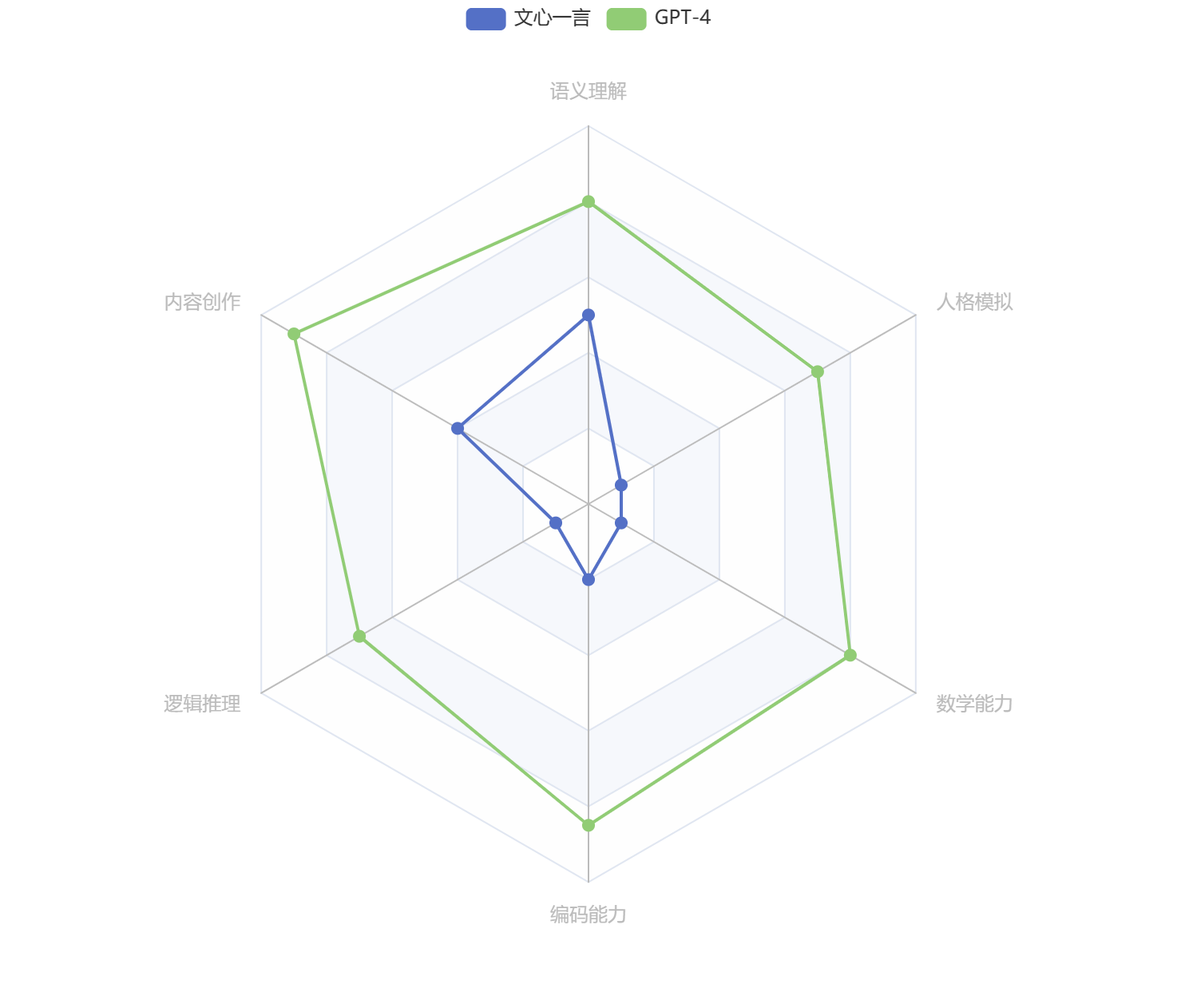
文心一言 vs GPT-4 —— 全面横向比较
文心一言 vs GPT-4 —— 全面横向比较 3月15日凌晨,OpenAI发布“迄今为止功能最强大的模型”——GPT-4。我第一时间为大家奉上了体验报告《OpenAI 发布GPT-4——全网抢先体验》。 时隔一日,3月16日下午百度发布大语言模型——文心一言。发布会上&#…...

rancher2.6进阶之kubectl安装
rancher2.6进阶之kubectl安装 1.安装kubectl客户端 1.1.1.使用命令行下载安装包: curl -LO https://dl.k8s.io/release/$(curl -L -s https://dl.k8s.io/release/stable.txt)/bin/linux/amd64/kubectl Note: 可指定下载版本, 将 ( c u r l − L − s h t t p s : / / d l . k …...

图像基本变换
缩放与裁剪裁剪图像的裁剪,是指将图像的某个区域切割出来。一些常见的应用场景包括:* 感兴趣区域提取* 去除无用信息* 图像增强* 纠偏:去除不规则部分,将图像变得更加整齐事实上,图像裁剪的裁剪通常就是一个numpy矩阵切…...
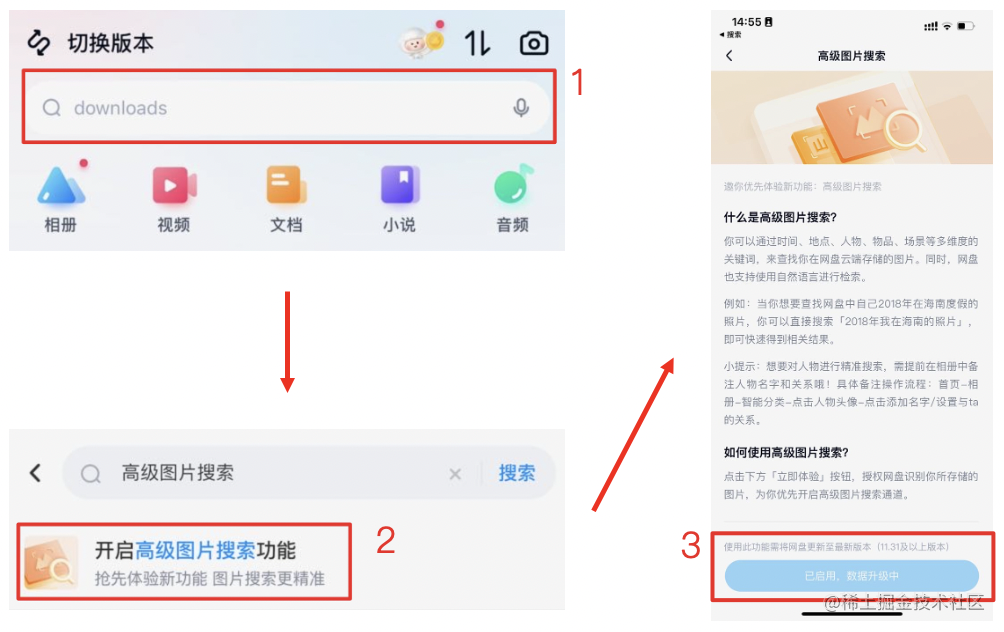
基于文心一言的底层视觉理解,百度网盘把「猫」换成了「黄色的猫」
随着移动互联网的一路狂飙,手机已经成为人们的新器官。出门不带钥匙可以,不带手机却是万万不可以的。而手机上,小小的摄像头也越来越成为各位「vlogger」的口袋魔方。每天有超过数亿的照片和视频被上传到百度网盘中,这些照片和视频…...

安卓开发的环境配置教程
文章目录事先准备:下载 JDK、Gradle下载安装 Android Studio下载安装 Android SDK下载安装 ADB笔者的环境: Java 17.0.1 Gradle 8.0.1 Android Studio Electric Eel | 2022.1.1 Patch 1 Windows 10 教育版 64位 事先准备:下载 JDK、Gradl…...

【Spring Cloud Alibaba】Spring Cloud Alibaba 搭建教程
文章目录教程适用版本一、简介主要功能组件开源地址二、开始搭建1.项目搭建与依赖管理2.服务注册与发现(Nacos安装)3.创建服务提供者4.创建服务消费者5.创建服务消费者(Feign)6.添加熔断机制(Sentinel)7.Sentinel熔断器仪表盘监控…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
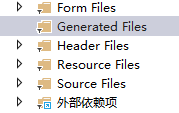
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...

项目进度管理软件是什么?项目进度管理软件有哪些核心功能?
无论是建筑施工、软件开发,还是市场营销活动,项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素,项目很容易陷入混乱,导致进度延误、成本超支,甚至失败。 项目进度管理软…...

Centos 7 服务器部署多网站
一、准备工作 安装 Apache bash sudo yum install httpd -y sudo systemctl start httpd sudo systemctl enable httpd创建网站目录 假设部署 2 个网站,目录结构如下: bash sudo mkdir -p /var/www/site1/html sudo mkdir -p /var/www/site2/html添加测试…...
