当前位置： 首页 > news >正文

中成科信票务管理系统 TicketManager.ashx接口SQL注入漏洞复现 [附POC]

news 2026/2/8 17:39:12

文章目录

  • 中成科信票务管理系统 TicketManager.ashx接口SQL注入漏洞复现 [附POC]
    • 0x01 前言
    • 0x02 漏洞描述
    • 0x03 影响版本
    • 0x04 漏洞环境
    • 0x05 漏洞复现
      • 1.访问漏洞环境
      • 2.构造POC
      • 3.复现
    • 0x06 修复建议

中成科信票务管理系统 TicketManager.ashx接口SQL注入漏洞复现 [附POC]

0x01 前言

免责声明：请勿利用文章内的相关技术从事非法测试，由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失，均由使用者本人负责，所产生的一切不良后果与文章作者无关。该文章仅供学习用途使用！！！

0x02 漏洞描述

中成科信票务管理系统是专注于演出剧院、体育场馆、旅游景区、游乐园、场地活动的票务管理系统,并为特殊客户量身定制票务应用解决方案，可根据用户的要求采用不同的技术载体实现门票的防伪:二维条码门票防伪技术、RFID电子门票防伪技术、手机二维码门票技术、变温微缩文字荧光等防伪票纸技术。

中成科信票务管理系统 TicketManager.ashx 接口处存在SQL注入漏洞复现，未经身份验证的恶意攻击者利用 SQL 注入漏洞获取数据库中的信息之外，攻击者甚至可以在高权限下向服务器写入命令，进一步获取服务器系统权限。

0x03 影响版本

中成科信票务管理系统

0x04 漏洞环境

FOFA语法：icon_hash=“-2142050529” || icon_hash=“1632964065”

相关文章：

中成科信票务管理系统 TicketManager.ashx接口SQL注入漏洞复现 [附POC]

文章目录 中成科信票务管理系统 TicketManager.ashx接口SQL注入漏洞复现 [附POC]0x01 前言0x02 漏洞描述0x03 影响版本0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.构造POC3.复现0x06 修复建议中成科信票务管理系统 TicketManager.ashx接口SQL注入漏洞复现 [附POC] 0x01 前言 …...

编程日记 2024/8/16 6:58:43

设计模式六大原则之：依赖倒置原则

1. 依赖倒置原则简介 依赖倒置原则(Dependency Inversion Principle, DIP) 是面向对象设计的核心原则之一，由罗伯特马丁(Robert C. Martin)提出，旨在降低类间的依赖度，使之更易于维护和扩展。该原则主张高层模块不应该依赖于底层模块&#x…...

编程日记 2024/8/16 6:55:39

06_Linux中如何让程序重启后自动启动

Linux中如何让程序重启后自动启动 systemd单元文件1.创建服务文件！！！服务配置文件的介绍 2.需要配置服务的状态（加载和启用服务）3.验证服务程序的运行状态4.打印程序的标准输出 systemd单元文件 Systemd 是现代 Linux…...

编程日记 2024/8/16 6:53:37

优化业务流程的关键：深入探讨BPA流程设计

在当前竞争激烈的商业环境中，业务流程自动化（BPA）已经成为企业提升效率、减少成本和提高业务灵活性的关键工具。今天，我们将深入探讨BPA流程设计的重要性及其实施步骤，为企业提供实用的指南。 什么是BPA？ …...

编程日记 2024/8/16 6:50:33

qt工程中调用sdl的流程

配置 Qt 工程 在你的 Qt 工程中，需要对项目文件（.pro 文件）进行配置，以包含 SDL 库的路径和链接选项。 # Qt Project File (.pro)# 设置 SDL 库的路径 INCLUDEPATH /path/to/SDL/include LIBS -L/path/to/SDL/lib -lSDL2初始化…...

编程日记 2024/8/16 6:49:32

ECMAScript性能优化技巧与陷阱

​ 大家好，我是程序员小羊！ 前言 ECMAScript，即JavaScript，是一种广泛应用于Web开发中的脚本语言。随着现代Web应用的复杂度日益增加，如何优化JavaScript的性能变得至关重要。性能优化不仅能提高应用的响应速度&#x…...

编程日记 2024/8/16 6:42:25

c++实现B树(上)

哈喽啊！好久不见，甚是想念！失踪人口要回归了，时隔一个多月小吉我终于要更新blog了🎉。在停更的一个多月中，小吉也有在好好学习提升自己，立志给大家呈现好文章。  现在让我们进入正题吧&#xf…...

编程日记 2024/8/16 6:41:23

【机器学习】深度强化学习–RL的基本概念、经典场景以及算法分类

引言 深度强化学习（Deep Reinforcement Learning, DRL）是机器学习的一个分支，它结合了深度学习（Deep Learning）和强化学习（Reinforcement Learning, RL）的技术 文章目录 引言一、深度强化学习–…...

编程日记 2024/8/16 6:40:21

【git】将本地文件上传到github

安装git 选择一个文件夹作为git仓库，cd到文件夹输入 git init文件夹出现.git文件夹，该文件夹默认为隐藏文件夹，设置为不隐藏 在cmd中输入 ssh-keygen -t rsa -C "xxxxxx.com"该邮箱为github邮箱，然后一路enter出现以…...

编程日记 2024/8/16 6:37:18

安卓应用开发学习：手机摇一摇功能应用尝试--摇骰子和摇红包

一、引言 前几天，我发布的日志《安卓应用开发学习：查看手机传感器信息》记录了如何查看手机传感器的信息，通过上述的方法，可以看到我的OPPO手机支持19种传感器。本篇日志就记录一下常见的加速度传感器的典型应用——“摇一摇”功…...

编程日记 2024/8/16 6:33:12

HTML中的＜fieldset＞标签元素框的使用

HTML 提供的 <fieldset> 标签用于在表单中分组相关元素。 <fieldset> 标签会在相关元素周围绘制一个框。 <legend> 标签为 fieldset 元素定义标题。 语法如下&#xff1a; <fieldset><legend>标题</legend><!-- 元素内容... -->…...

编程日记 2024/8/16 6:32:10

Linux驱动入门实验班——SR501红外模块驱动（附百问网视频链接）

目录 一、工作方式 二、接口图 三、编写思路 1.构造file_operations结构体 2.实现read函数 3.编写入口函数 4.编写中断处理函数 5.编写出口函数 6.声明出入口函数以及协议 四、源码 五、课程链接 一、工作方式 SR501人体红外感应模块有两种工作模式&#xff1a; …...

编程日记 2024/8/16 6:31:08

windows C++- Com技术简介(上)

在介绍C和winrt与COM组件技术的关系之前&#xff0c;有必要介绍一下com组件技术&#xff0c;这项技术比较古老&#xff0c;但是它一直作为windows的基石存在。COM 是一类独立于平台且面向对象的分布式系统&#xff0c;用于创建可交互的二进制软件组件。 COM 技术是 Microsoft O…...

编程日记 2024/8/16 6:30:07

Jenkins持续集成工具学习

一、从装修厨房看项目开发效率优化 二、持续集成工具 三、JavaEE项目部署方式对比 四、JenkinsSVN持续集成环境搭建 五、JenkinsGitHub持续集成环境搭建...

编程日记 2024/8/16 6:29:06

Redis：查询是否包含某个字符/字符串之三

上一篇&#xff1a;Redis&#xff1a;查询是否包含某个字符/字符串之二-CSDN博客 摘要&#xff1a; 遍历key&#xff0c;在跟进value的类型遍历value是否包含指定字符串 search_strings &#xff0c;这里使用redis-py库&#xff0c;默认只能处理utf-8编码&#xff0c;如果存在…...

编程日记 2024/8/16 6:27:03

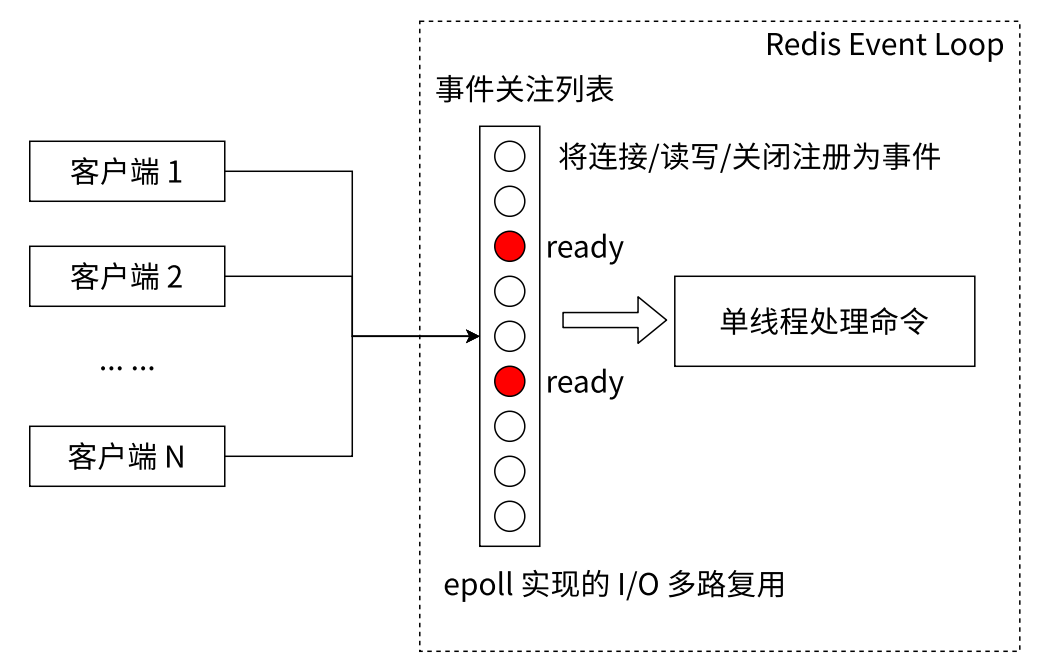
【Redis】数据类型详解及其应用场景

目录 Redis 常⻅数据类型预备知识基本全局命令小结 数据结构和内部编码单线程架构引出单线程模型为什么单线程还能这么快 Redis 常⻅数据类型 Redis 提供了 5 种数据结构&#xff0c;理解每种数据结构的特点对于 Redis 开发运维⾮常重要&#xff0c;同时掌握每种数据结构的常⻅…...

编程日记 2024/8/16 6:26:01

PARA-Drive：设计并行模型实现端到端自动驾驶

论文链接 https://openaccess.thecvf.com/content/CVPR2024/papers/Weng_PARA-Drive_Parallelized_Architecture_for_Real-time_Autonomous_Driving_CVPR_2024_paper.pdfhttps://openaccess.thecvf.com/content/CVPR2024/papers/Weng_PARA-Drive_Parallelized_Architecture_fo…...

编程日记 2024/8/16 6:23:59

vs2022 x64 C/C++和汇编混编 遇到的坑

vs2022 x64 C/C和汇编混编 遇到的坑 遇到的问题二、问题复现1.出错代码2.问题分析2.1 堆栈对齐问题 3.解决方案 总结奇数和偶数个寄存器的影响为什么 sub rsp, 8 对奇数个寄存器有用&#xff1f;结论 遇到的问题 0x00007FFFFAE24A29 (msvcp140.dll)处(位于 TestCompileConsole…...

编程日记 2024/8/16 6:21:56

PHP概述、环境搭建与基本语法讲解

目录 【学习目标、重难点知识】 什么是网站&#xff1f; 1. PHP 介绍 1.1. PHP 概述 1.1.1. PHP 是什么&#xff1f; 1.1.2. PHP 都能做什么&#xff1f; 1.2. PHP 环境搭建 1.2.1. PhpStudy 2. PHP 基本语法 2.1. PHP 语法入门 2.1.1. 第一个 PHP 程序 2.1.2. PHP …...

编程日记 2024/8/16 6:20:55

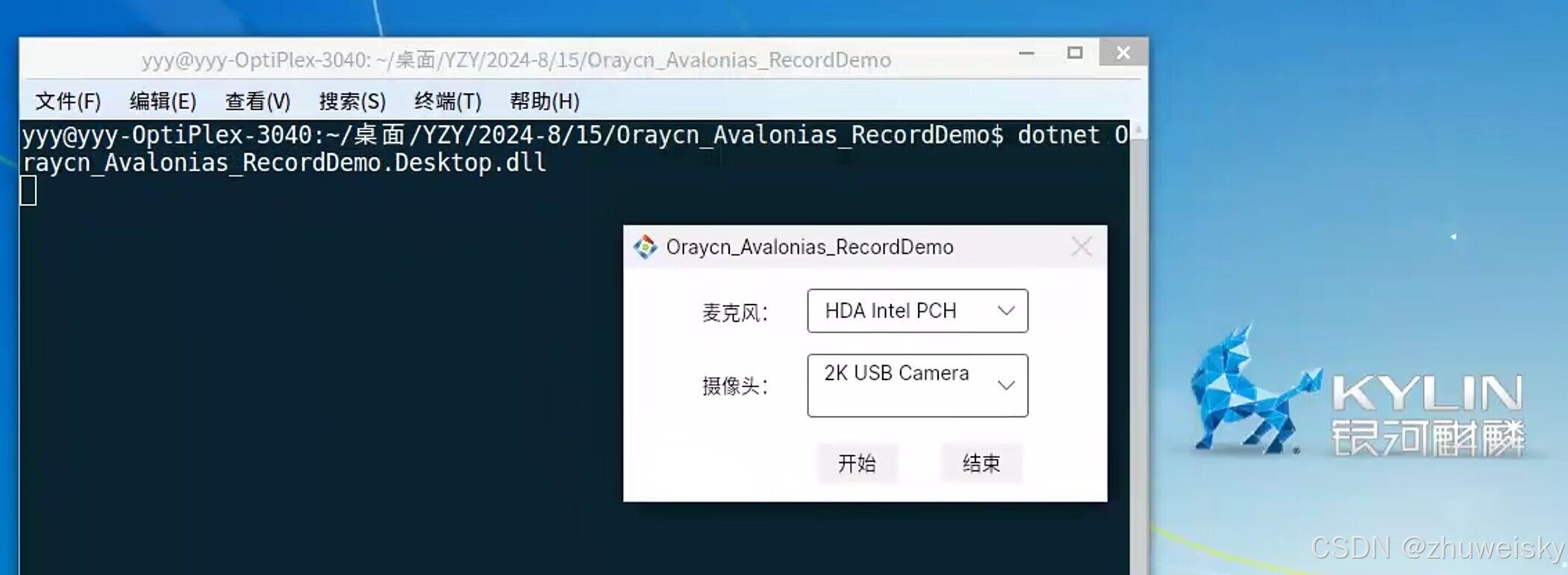
实现信创Linux麦克风摄像头录制（源码，银河麒麟、统信UOS）

随着信创国产化浪潮的来临&#xff0c;在国产操作系统上的应用开发的需求越来越多&#xff0c;其中一个就是需要在银河麒麟或统信UOS上实现录制摄像头视频和麦克风声音&#xff0c;将它们录制成一个mp4文件。那么这个要如何实现了&#xff1f; 一. 技术方案 要完成这些功能&a…...

编程日记 2024/8/16 6:19:53

Lombok 的 @Data 注解失效，未生成 getter/setter 方法引发的HTTP 406 错误

HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误&#xff0c;它们的含义、原因和解决方法都有显著区别。以下是详细对比&#xff1a; 1. HTTP 406 (Not Acceptable) 含义&#xff1a; 客户端请求的内容类型与服务器支持的内容类型不匹…...

编程新知 2026/2/1 20:49:03

docker详细操作--未完待续

docker介绍 docker官网: Docker&#xff1a;加速容器应用程序开发 harbor官网&#xff1a;Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台&#xff0c;用于将应用程序及其依赖项&#xff08;如库、运行时环…...

编程新知 2026/2/5 4:33:24

遍历 Map 类型集合的方法汇总

1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

编程新知 2026/1/24 15:08:45

无法与IP建立连接，未能下载VSCode服务器

如题&#xff0c;在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈&#xff0c;发现是VSCode版本自动更新惹的祸&#xff01;&#xff01;&#xff01; 在VSCode的帮助->关于这里发现前几天VSCode自动更新了&#xff0c;我的版本号变成了1.100.3 才导致了远程连接出…...

编程新知 2026/1/22 21:24:01

Python实现prophet 理论及参数优化

文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候&#xff0c;写过一篇简单实现&#xff0c;后期随着对该模型的深入研究&#xff0c;本次记录涉及到prophet 的公式以及参数调优&#xff0c;从公式可以更直观…...

编程新知 2026/1/27 5:01:54

Unity | AmplifyShaderEditor插件基础（第七集：平面波动shader）

目录 一、&#x1f44b;&#x1f3fb;前言 二、&#x1f608;sinx波动的基本原理 三、&#x1f608;波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、&#x1f30a;波动优化…...

编程新知 2026/2/6 22:55:12

Redis的发布订阅模式与专业的 MQ（如 Kafka, RabbitMQ）相比，优缺点是什么？适用于哪些场景？

Redis 的发布订阅&#xff08;Pub/Sub&#xff09;模式与专业的 MQ&#xff08;Message Queue&#xff09;如 Kafka、RabbitMQ 进行比较&#xff0c;核心的权衡点在于&#xff1a;简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

编程新知 2025/12/4 2:32:37

【分享】推荐一些办公小工具

1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由&#xff1a;大部分的转换软件需要收费&#xff0c;要么功能不齐全&#xff0c;而开会员又用不了几次浪费钱&#xff0c;借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

编程新知 2026/1/25 14:40:59

STM32HAL库USART源代码解析及应用

STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

编程新知 2026/1/31 13:18:46

MySQL 8.0 事务全面讲解

以下是一个结合两次回答的 MySQL 8.0 事务全面讲解&#xff0c;涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容&#xff0c;并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念&#xff08;ACID&#xff09; 事务是…...

编程新知 2025/9/19 22:12:36