小白零基础学数学建模应用系列(五):任务分配问题优化与求解
文章目录
- 一. 分配问题
- 1.1 问题背景
- 1.2 假设条件
- 1.3 问题要求
- 1.4 数学建模
- 二. 实际案例
- 2.1 问题背景
- 2.2 假设条件
- 2.3 问题要求
- 2.4 模型建立
- 2.5 求解代码
- 2.6 结果分析
- 2.6.1 分配方案的解释
- 2.6.2 总时间的优化
- 2.6.3 潜在的现实应用
一. 分配问题
1.1 问题背景
分配问题(Assignment Problem)是运筹学中的经典问题之一,广泛应用于生产调度、任务分配、人员调度等领域。其核心思想是将一定数量的资源合理分配到一定数量的任务中,以达到最优的效果。在实际应用中,资源和任务的分配通常是基于某种目标,例如最小化总成本、时间或最大化总效率等。
在本文中,我们研究的是一个典型的分配问题:设有 (m) 件工作和 (m) 个人员,每个人只能完成一项工作,且每项工作只能分配给一个人。已知第 (i) 个人完成第 (j) 项工作的时间(或费用)为 c i j c_{ij} cij,我们的目标是如何分配这些工作,使得总时间(或总费用)最少。
1.2 假设条件
在求解这个问题之前,我们需要作出以下假设条件:
- 工作数量与人员数量相同:即有 (m) 件工作和 (m) 个人员,确保每个工作都有人负责且每个人只负责一项工作。
- 每个人都有能力完成分配的工作:假设每个任务对于被分配的人员都是可行的,即每个 c i j c_{ij}\ cij 是一个有限值。
- 工作独立性:各项工作之间是独立的,完成某一项工作所需的时间或费用不会因其他工作的分配而改变。
- 分配不可拆分:每项工作只能由一个人完成,不能将工作拆分给多个人员。
1.3 问题要求
根据上述背景和假设,问题的要求可以表述为:
给定一个 m × m m \times m\ m×m 的矩阵 C = [ c i j ] C = [c_{ij}] C=[cij],其中 c i j c_{ij} cij 表示第 (i) 个人完成第 (j) 项工作的时间(或费用)。需要找到一个分配方案,使得总的完成时间(或总费用)最小化。
好的,我们将基于你提供的截图内容,采用0-1规划来建立模型,并给出相应的求解代码。
1.4 数学建模
首先,我们定义决策变量:
x i j = { 1 如果第 i 个人被分配做第 j 件工作, 0 否则。 x_{ij} = \begin{cases} 1 & \text{如果第 } i \text{ 个人被分配做第 } j \text{ 件工作,}\\ 0 & \text{否则。} \end{cases} xij={10如果第 i 个人被分配做第 j 件工作,否则。
目标函数为:
minimize z = ∑ i = 1 m ∑ j = 1 m c i j x i j \text{minimize } z = \sum_{i=1}^{m} \sum_{j=1}^{m} c_{ij}x_{ij} minimize z=i=1∑mj=1∑mcijxij
约束条件为:
∑ j = 1 m x i j = 1 , i = 1 , 2 , … , m \sum_{j=1}^{m} x_{ij} = 1, \quad i = 1, 2, \dots, m j=1∑mxij=1,i=1,2,…,m
∑ i = 1 m x i j = 1 , j = 1 , 2 , … , m \sum_{i=1}^{m} x_{ij} = 1, \quad j = 1, 2, \dots, m i=1∑mxij=1,j=1,2,…,m
x i j ∈ { 0 , 1 } , i , j = 1 , 2 , … , m x_{ij} \in \{0, 1\}, \quad i, j = 1, 2, \dots, m xij∈{0,1},i,j=1,2,…,m
二. 实际案例
为了更好地理解和展示该问题的实际应用,我们将假设一个具体的场景,并给出相应的参数值用于建模和求解。
2.1 问题背景
假设某公司正在进行一个项目,需要分配任务给不同的员工。公司有4个任务和4名员工,每个员工完成每个任务所需的时间(或成本)是已知的。公司希望通过合理分配任务,使得所有任务的总完成时间最短。
具体任务与员工的时间表如下:
- 任务A、B、C、D
- 员工1、2、3、4
下表为每个员工完成每项任务所需的时间(单位:小时):
| 任务A | 任务B | 任务C | 任务D | |
|---|---|---|---|---|
| 员工1 | 13 | 4 | 7 | 6 |
| 员工2 | 1 | 11 | 5 | 4 |
| 员工3 | 6 | 7 | 2 | 8 |
| 员工4 | 1 | 3 | 5 | 9 |
2.2 假设条件
我们沿用之前提到的假设条件:
- 公司有4个任务和4名员工,确保每个任务都能被完成,且每个员工只负责一项任务。
- 每个员工都有能力完成分配给他的任何任务,时间表中的数值表示了完成任务所需的时间。
- 各项任务之间是独立的,完成某一项任务的时间不会因其他任务的分配而改变。
- 每个任务只能由一个员工完成,不能将任务拆分给多个人员。
2.3 问题要求
基于上述背景,问题的要求是找到一个最优的任务分配方案,使得所有任务的总完成时间最短。
2.4 模型建立
我们可以根据上表的具体数据构建0-1规划模型。具体来说,设定 ( m = 4 ) 和 ( n = 4 )(即4个任务和4名员工),然后我们将每个员工完成每项任务的时间用一个4x4的矩阵表示:
c i j = ( 13 4 7 6 1 11 5 4 6 7 2 8 1 3 5 9 ) c_{ij} = \begin{pmatrix} 13 & 4 & 7 & 6 \\ 1 & 11 & 5 & 4 \\ 6 & 7 & 2 & 8 \\ 1 & 3 & 5 & 9 \\ \end{pmatrix} cij= 131614117375256489
目标函数为:
minimize z = ∑ i = 1 4 ∑ j = 1 4 c i j x i j \text{minimize } z = \sum_{i=1}^{4} \sum_{j=1}^{4} c_{ij}x_{ij} minimize z=i=1∑4j=1∑4cijxij
约束条件为:
∑ j = 1 4 x i j = 1 , i = 1 , 2 , 3 , 4 \sum_{j=1}^{4} x_{ij} = 1, \quad i = 1, 2, 3, 4 j=1∑4xij=1,i=1,2,3,4
∑ i = 1 4 x i j = 1 , j = 1 , 2 , 3 , 4 \sum_{i=1}^{4} x_{ij} = 1, \quad j = 1, 2, 3, 4 i=1∑4xij=1,j=1,2,3,4
x i j ∈ { 0 , 1 } , i , j = 1 , 2 , 3 , 4 x_{ij} \in \{0, 1\}, \quad i, j = 1, 2, 3, 4 xij∈{0,1},i,j=1,2,3,4
2.5 求解代码
我们Python代码进行求解:
import pulp# 定义cij矩阵,表示第i个人完成第j项工作的时间
c = [[13, 4, 7, 6],[1, 11, 5, 4],[6, 7, 2, 8],[1, 3, 5, 9]
]# 初始化问题
prob = pulp.LpProblem("Assignment_Problem", pulp.LpMinimize)# 决策变量定义
x = pulp.LpVariable.dicts("x", (range(4), range(4)), cat='Binary')# 目标函数
prob += pulp.lpSum([c[i][j] * x[i][j] for i in range(4) for j in range(4)])# 约束条件:每个人只能被分配到一项工作
for i in range(4):prob += pulp.lpSum([x[i][j] for j in range(4)]) == 1# 约束条件:每项工作只能分配给一个人
for j in range(4):prob += pulp.lpSum([x[i][j] for i in range(4)]) == 1# 求解问题
prob.solve()# 输出结果
print("Optimal Assignment:")
for i in range(4):for j in range(4):if x[i][j].value() == 1:print(f"Person {i+1} assigned to Job {j+1} with time {c[i][j]} hours")print("Total minimum time:", pulp.value(prob.objective), "hours")
运行结果如下:
Optimal Assignment:
Person 1 assigned to Job 2 with time 4 hours
Person 2 assigned to Job 4 with time 4 hours
Person 3 assigned to Job 3 with time 2 hours
Person 4 assigned to Job 1 with time 1 hours
Total minimum time: 11.0 hours
2.6 结果分析
通过运行线性规划模型,我们得到了最优的任务分配方案,目标是使所有任务的总完成时间最短。最终的最优分配结果如下:
- 员工1 被分配完成 任务B,所需时间为 4小时。
- 员工2 被分配完成 任务D,所需时间为 4小时。
- 员工3 被分配完成 任务C,所需时间为 2小时。
- 员工4 被分配完成 任务A,所需时间为 1小时。
总的最小完成时间为 11小时。
2.6.1 分配方案的解释
-
员工1 被分配到 任务B,所需时间为4小时。在给定的时间矩阵中,员工1的其他任务选项中时间更长(13小时、7小时、6小时),因此选择4小时的任务B是最佳选择。
-
员工2 被分配到 任务D,所需时间为4小时。虽然员工2完成任务A仅需1小时,但由于任务A已经被分配给了更合适的员工4,员工2只能选择任务D。相比其他选项(11小时和5小时),选择任务D的4小时是最优的。
-
员工3 被分配到 任务C,所需时间为2小时。对于员工3来说,这是所有可选任务中时间最短的,因此是最优的选择。
-
员工4 被分配到 任务A,所需时间为1小时。对于员工4来说,任务A是耗时最短的,尽管其他任务的时间相对较长(3小时、5小时、9小时),因此这是最佳分配。
2.6.2 总时间的优化
该分配方案达到了最小化总时间的目标,总时间为 11小时。相比于其他可能的分配组合,这个方案有效地利用了每个员工的优势,并合理地分配了任务。以下几点进一步说明了方案的优越性:
-
最小化完成时间:通过合理分配,所有任务的完成时间被压缩到最小。这确保了项目在最短的时间内完成,提高了整体效率。
-
任务和资源的匹配:每个员工都被分配到最适合的任务,这不仅降低了总完成时间,还有效减少了可能的资源浪费和时间超支。
2.6.3 潜在的现实应用
在实际应用中,这种任务分配方法可以用于多个场景,比如生产调度、人力资源管理、项目管理等。在这些场景中,合理的资源分配不仅能够节省时间,还能提高整体效率和生产力。
总之,本文所提供的分配方案和分析展示了如何通过线性规划技术,优化资源分配,解决复杂的现实问题。这种方法简单有效,具有广泛的应用前景。
相关文章:
:任务分配问题优化与求解)
小白零基础学数学建模应用系列(五):任务分配问题优化与求解
文章目录 一. 分配问题1.1 问题背景1.2 假设条件1.3 问题要求1.4 数学建模 二. 实际案例2.1 问题背景2.2 假设条件2.3 问题要求2.4 模型建立2.5 求解代码2.6 结果分析2.6.1 分配方案的解释2.6.2 总时间的优化2.6.3 潜在的现实应用 一. 分配问题 1.1 问题背景 分配问题&#x…...

怎么防止源代码泄露?十种方法杜绝源代码泄密风险
源代码是软件开发的核心资产之一,保护其不被泄露对企业的安全至关重要。源代码泄露不仅可能导致知识产权的丧失,还可能给企业带来经济损失和品牌形象的损害。以下是十种有效的方法,可以帮助企业杜绝源代码泄密的风险。 1. 代码加密 对源代码…...
uniapp left right 的左右模态框
标题 这是组件 <template><div class"content-wrapper"><divv-for"(vla, i) in products":key"i":class"[content-page, getPageClass(i)]"><slot :data"vla"><!-- 用户自定义的内容 --><…...
Docker Compose与私有仓库部署
一、Docker Compose工具 1.1什么是Docker Compose Docker Compose 的前身是 Fig,它是一个定义及运行多个 Docker 容器的工具。使用Docker Compose 时,只需要在一个配置文件中定义多个 Docker 容器,然后使用一条命令启 动这些容器。Docker Co…...
Layout 布局组件快速搭建
文章目录 设置主题样式变量封装公共布局组件封装 Logo 组件封装 Menu 菜单组件封装 Breadcrumb 面包屑组件封装 TabBar 标签栏组件封装 Main 内容区组件封装 Footer 底部组件封装 Theme 主题组件 经典布局水平布局响应式布局搭建 Layout 布局组件添加 Layout 路由配置启动项目 …...

北京城市图书馆-非遗文献馆:OLED透明拼接屏的璀璨应用
在数字化与传统文化深度融合的今天,北京城市图书馆的非遗文献馆以一场前所未有的视觉盛宴,向世人展示了OLED透明拼接屏的非凡魅力与无限可能。这座集阅读、展示、体验于一体的非遗文献馆,通过2*7布局的OLED透明拼接屏,不仅为传统非…...

OpenCV图像滤波(12)图像金字塔处理函数pyrDown()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 函数主要是对图像进行模糊处理并将其降采样。 默认情况下,输出图像的大小计算为 Size((src.cols1)/2, (src.rows1)/2),但…...

css如何使一个盒子水平垂直居中
方法一:利用定位(常用方法,推荐) <style> .parent{width: 500px;height: 500px;border: 1px solid #000;position:relative; }.child {width: 100px;height: 100px;border: 1px solid #999;position:absolute;top: 50%;left: 50%;margin-top: -50…...

机器人等方向学习和研究的目标
核心目标类似: 学习一个知识点用时越来越短,研究一个系统效率越来越高。 目标 没有目标是常态,十分普遍。 但其实,目标也可以很宽泛。 感谢朋友们一直以来的鼓励帮助,倍感荣幸,非常感谢。-CSDN blink-…...
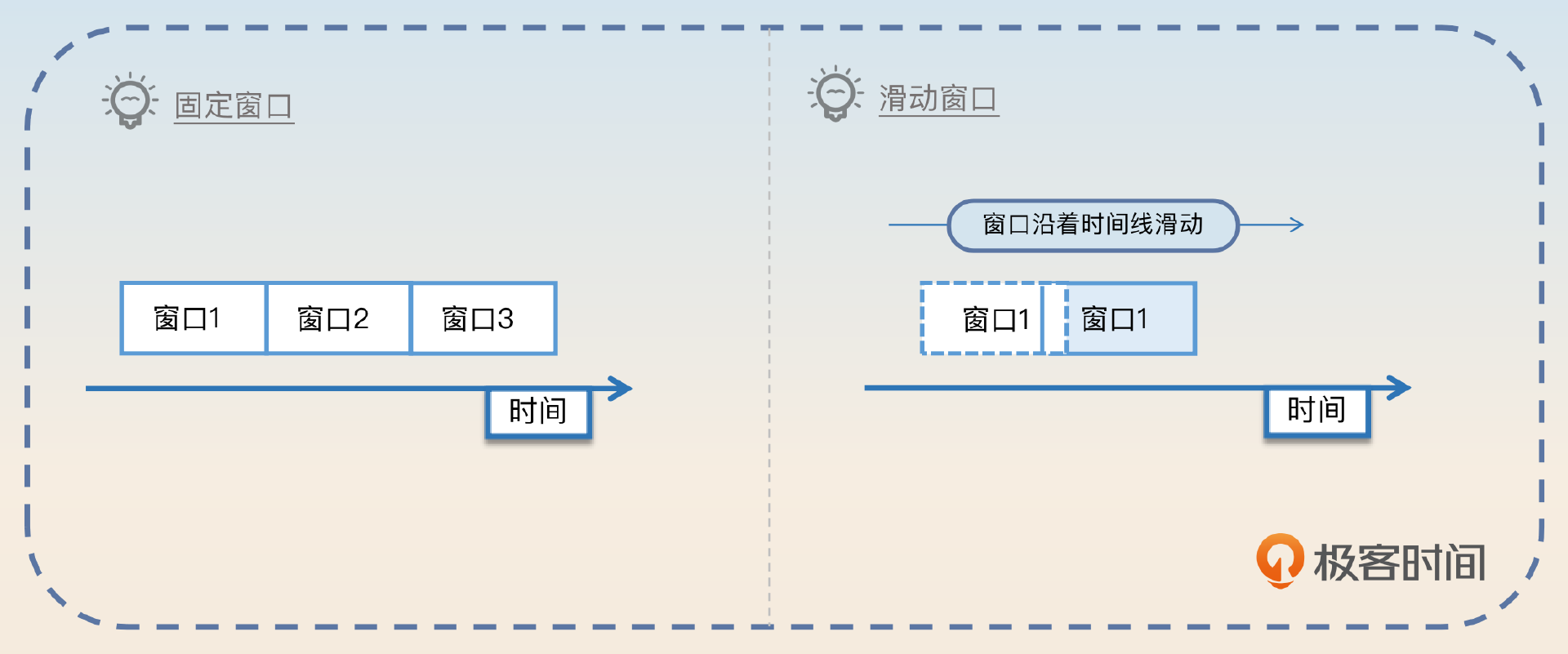
封装一个细粒度的限流器
文章目录 原因限流对象限流后的做法怎么确定限流阈值观测业务性能数据压测借鉴链路上的其他服务手动计算 四种静态限流算法令牌桶漏桶固定窗口与滑动窗口 手写限流算法令牌桶漏桶固定窗口滑动窗口 分布式限流的具体实现 原因 尽管云原生网关里有统一入口的限流(根据…...

【Spring Boot - 注解】@ResponseBody 注解:处理 JSON 响应
文章目录 一、ResponseBody 注解概述1. 注解的功能2. 主要功能 二、ResponseBody 的工作原理1. 接口定义2. 消息转换器3. 自动配置与默认行为 三、ResponseBody 的应用场景1. RESTful API 的实现2. 返回复杂数据结构3. 错误处理和异常处理 四、ResponseBody 的配置和自定义1. 自…...
无人机航拍与ArcGIS融合实战:从地表观测到空间数据可视化的全方位指南!无人机图像拼接数据处理与分析、可视化与制图
目录 第一章 无人机航拍基本流程、航线规划与飞行实践 第二章 无人机图像拼接软件的学习与操作实践 第三章 无人机图像拼接典型案例详解 第四章 无人机图像拼接数据在GIS中的处理与分析 第五章 无人机图像拼接数据在GIS中的可视化与制图 第六章 综合案例:无人机航拍植被动…...
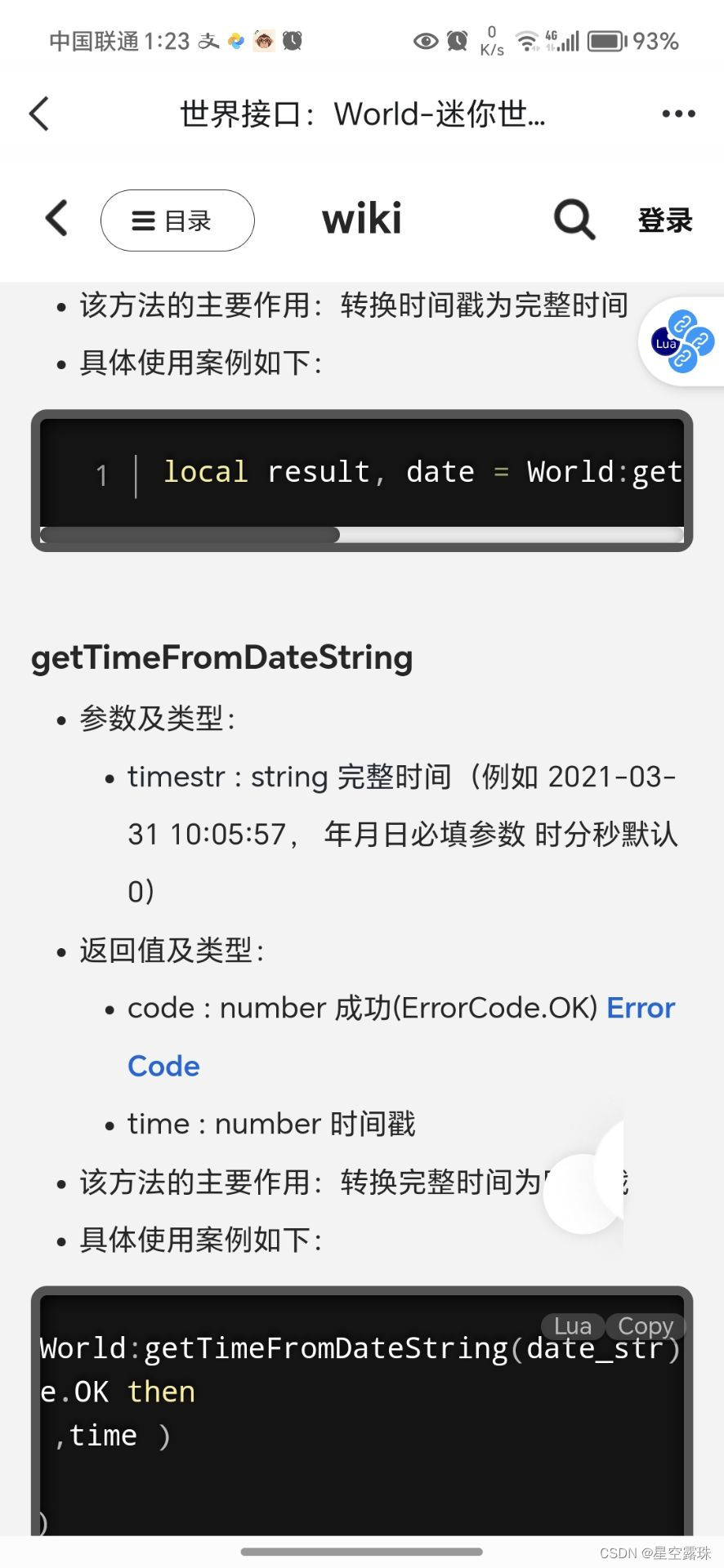
日期转时间濯
tfunction(date_str) local code ,time World:getTimeFromDateString(date_str) return time/(60*60*24) end print(t(2024-08-16)-t(2024-08-3))...
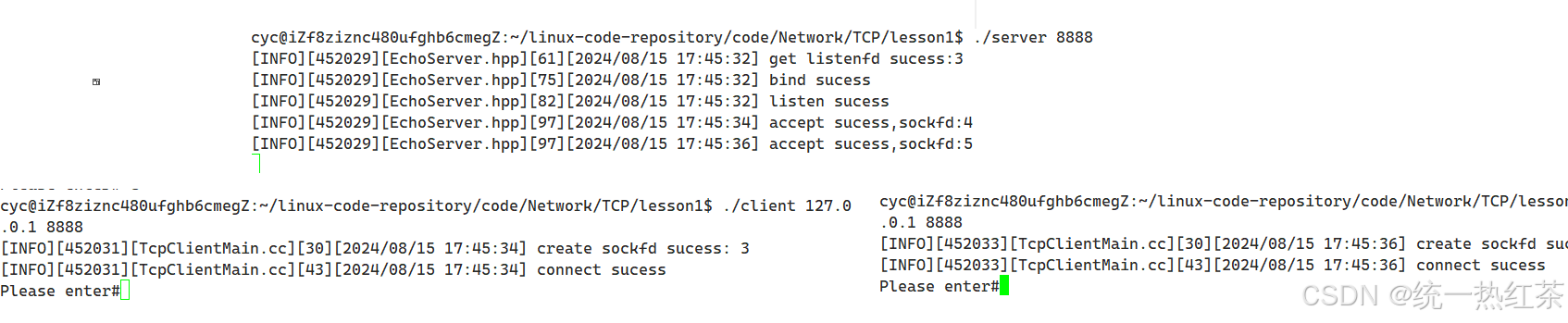
【计算机网络】TCP实战
其实有了UDP的基础,TCP不管怎么说学习起来都还是比较舒服的,至少是比直接就学习TCP的感觉好。 这篇文章最多就是介绍一下起手式,如果想带业务的话和UDP那篇是完全一样的,就不进行演示了。 总的来说还是很简单的。 目录 Echo服务端…...

使用Python制作贪吃蛇小游戏
引言 贪吃蛇游戏是一款经典的电子游戏,玩家通过控制一条不断增长的蛇在格子内移动,并吃掉随机出现的食物来获得分数。随着分数的增加,蛇的身体也会越来越长,游戏的难度也随之提升。在本文中,我们将详细介绍如何使用Py…...

线程的退出
方式1 pthread_exit Void pthread_exit (void *retval) 功能: 结束调用的线程 参数: retval //退出状态值 //需要传的是,退出状态值的地址 注意: 1.pthread_exit 本身表示结束线程 如果用在main函数中 表示结束主线程…...
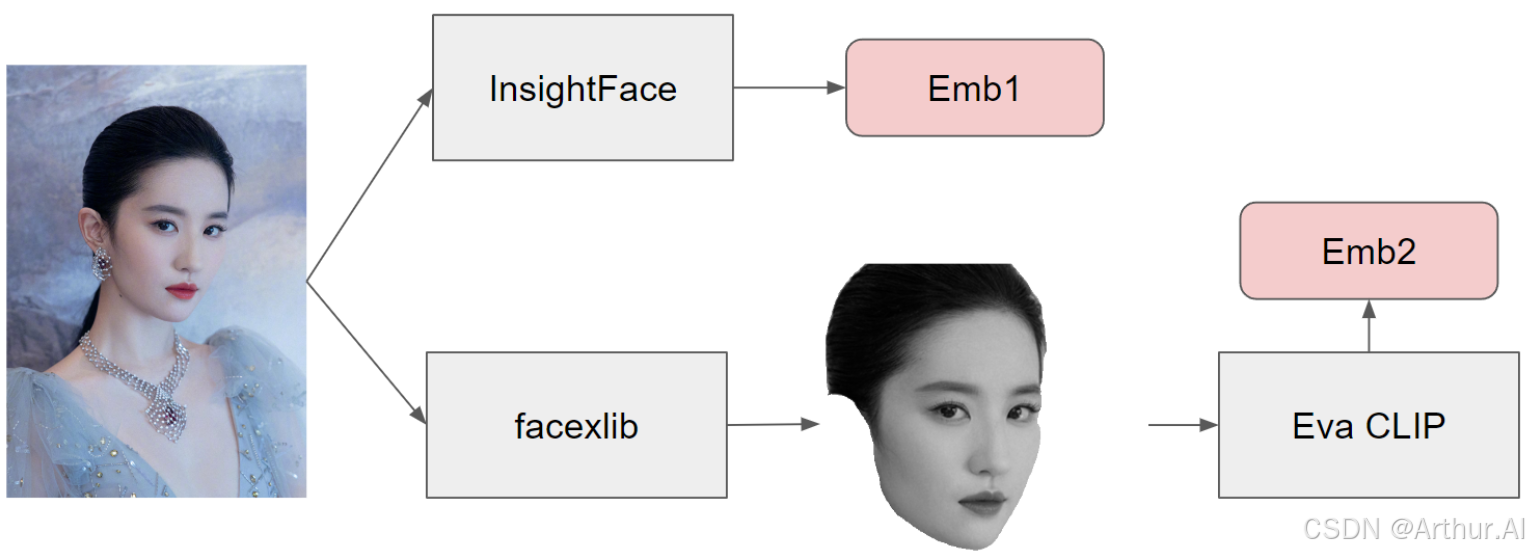
【AI 绘画】Q版人物定制生成
AI 绘画-PulID手办定制 1. 效果展示 本次测试主要结果展示如下: 牛仔风 古风 2. 基本原理 PuLID是一种类似于 ip-adapter 的恢复面部特征的方法。它同时使用 insightface 嵌入和 CLIP 嵌入,类似于 ip-adapter faceid plus 模型所做的。但是,在将图像传递给 CLIP 之前,还…...
Python爬虫——爬取某网站的视频
爬取视频 本次爬取,还是运用的是requests方法 首先进入bilibili官网中,选取你想要爬取的视频,进入视频播放页面,按F12,将网络中的名称栏向上拉找到第一个并点击,可以在标头中,找到后续我们想要…...

Android逆向题解攻防世界-easy-apk
Jeb反编译apk 题目比较简单,就是一个改了码表的base64编码。 protected void onCreate(Bundle savedInstanceState) {super.onCreate(savedInstanceState);this.setContentView(0x7F04001B); // layout:activity_main((Button)this.findViewById(0x7F0B0076)).set…...
Linux系统使用Typecho搭建个人网站并一键发布公网远程管理本地站点
文章目录 前言1. 安装环境2. 下载Typecho3. 创建站点4. 访问Typecho5. 安装cpolar6. 远程访问Typecho7. 固定远程访问地址8. 配置typecho 💡 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
