代码随想录训练营 Day32打卡 动态规划 part01 理论基础 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
代码随想录训练营 Day32打卡 动态规划 part01
一、 理论基础
动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
例如:有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
动态规划中dp[j]是由dp[j-weight[i]]推导出来的,然后取max(dp[j], dp[j - weight[i]] + value[i])。
但如果是贪心呢,每次拿物品选一个最大的或者最小的就完事了,和上一个状态没有关系。
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
二、 力扣509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 :
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
版本一
如果 n 为 0,直接返回 0,这是 Fibonacci 序列的第一个值。
创建一个长度为 n + 1 的数组 dp,用于存储从第 0 到第 n 位的 Fibonacci 值。
dp[0] 和 dp[1] 分别初始化为 0 和 1,对应 Fibonacci 序列的前两个值。
从 i = 2 开始遍历,使用状态转移方程 dp[i] = dp[i - 1] + dp[i - 2] 计算每个位置的 Fibonacci 值。
最终返回 dp[n],即为第 n 个 Fibonacci 数。
class Solution:def fib(self, n: int) -> int:# 排除 Corner Case,当 n 为 0 时,直接返回 0if n == 0:return 0# 创建 dp table 用于存储每个位置的 Fibonacci 值dp = [0] * (n + 1)# 初始化 dp 数组,Fibonacci 序列的前两个值dp[0] = 0dp[1] = 1# 遍历顺序: 由前向后。因为后面要用到前面的状态for i in range(2, n + 1):# 确定递归公式/状态转移公式dp[i] = dp[i - 1] + dp[i - 2] # dp[i] 等于前两个状态的和# 返回答案,dp[n] 即为第 n 个 Fibonacci 数return dp[n]版本二
如果 n 小于等于 1,直接返回 n,因为 Fibonacci(0) = 0 和 Fibonacci(1) = 1。
使用一个长度为 2 的列表 dp 来存储最近的两个 Fibonacci 值,初始为 [0, 1]。
从 i = 2 开始循环计算 Fibonacci 数,每次计算当前 Fibonacci 数并更新 dp 列表中的值。
返回 dp[1],即为第 n 个 Fibonacci 数。
class Solution:def fib(self, n: int) -> int:# 如果 n 小于等于 1,直接返回 n(因为 Fibonacci(0) = 0, Fibonacci(1) = 1)if n <= 1:return n# 初始化 dp 数组,只保存最近的两个 Fibonacci 数dp = [0, 1]# 从 2 开始计算到 nfor i in range(2, n + 1):# 计算当前 Fibonacci 数,并更新 dp 数组total = dp[0] + dp[1]dp[0] = dp[1] # 将 dp[1] 移到 dp[0] 位置dp[1] = total # 新的 Fibonacci 数放在 dp[1] 位置# 返回 dp[1],即为第 n 个 Fibonacci 数return dp[1]版本三
如果 n 小于等于 1,直接返回 n,因为 Fibonacci(0) = 0 和 Fibonacci(1) = 1。
使用 prev1 和 prev2 分别存储前两个 Fibonacci 数,初始为 0 和 1。
从 i = 2 开始计算,每次更新 prev1 和 prev2,其中 curr 是当前计算出的 Fibonacci 数。
返回 prev2,即为第 n 个 Fibonacci 数。
class Solution:def fib(self, n: int) -> int:# 如果 n 小于等于 1,直接返回 nif n <= 1:return n# 使用两个变量存储前两个 Fibonacci 数prev1, prev2 = 0, 1# 从 2 开始计算到 nfor _ in range(2, n + 1):# 当前 Fibonacci 数是前两个数之和curr = prev1 + prev2# 更新 prev1 和 prev2prev1, prev2 = prev2, curr# 返回最后的 Fibonacci 数return prev2力扣题目链接
题目文章讲解
题目视频讲解
三、 力扣70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
dp[i]的定义:爬到第i层楼梯,有dp[i]种方法。
举例当n为5的时候,dp table(dp数组)应该是这样的

代码实现
如果 n 小于等于 1,直接返回 n。
通过使用两个变量 prev1 和 prev2 分别存储前两个台阶的方法数,进一步优化空间复杂度到 O(1)。
计算当前台阶的方法数 total,并更新 prev1 和 prev2,继续计算下一个台阶的方法数。
返回 prev2,即为到达第 n 级台阶的方法数。
# 空间复杂度为 O(1) 版本
class Solution:def climbStairs(self, n: int) -> int:# 处理边界情况,如果楼梯数为1或更少,直接返回n(0或1)if n <= 1:return n# 使用两个变量来存储前两个台阶的方法数,节省空间prev1 = 1 # 表示前两级台阶的方法数prev2 = 2 # 表示前一级台阶的方法数# 从第3级台阶开始计算for i in range(3, n + 1):# 当前台阶的方法数是前两个台阶的方法数之和total = prev1 + prev2prev1 = prev2 # 更新 prev1 为前一级台阶的方法数prev2 = total # 更新 prev2 为当前台阶的方法数# 返回到达第n级台阶的方法数return prev2力扣题目链接
题目文章讲解
题目视频讲解
四、力扣746. 使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 :
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
对于dp数组的定义,大家一定要清晰!
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:

版本一
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:dp = [0] * (len(cost) + 1)dp[0] = 0 # 初始值,表示从起点开始不需要花费体力dp[1] = 0 # 初始值,表示经过第一步不需要花费体力for i in range(2, len(cost) + 1):# 在第i步,可以选择从前一步(i-1)花费体力到达当前步,或者从前两步(i-2)花费体力到达当前步# 选择其中花费体力较小的路径,加上当前步的花费,更新dp数组dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])return dp[len(cost)] # 返回到达楼顶的最小花费版本二
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:dp0 = 0 # 初始值,表示从起点开始不需要花费体力dp1 = 0 # 初始值,表示经过第一步不需要花费体力for i in range(2, len(cost) + 1):# 在第i步,可以选择从前一步(i-1)花费体力到达当前步,或者从前两步(i-2)花费体力到达当前步# 选择其中花费体力较小的路径,加上当前步的花费,得到当前步的最小花费dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2])dp0 = dp1 # 更新dp0为前一步的值,即上一次循环中的dp1dp1 = dpi # 更新dp1为当前步的最小花费return dp1 # 返回到达楼顶的最小花费力扣题目链接
题目文章讲解
题目视频讲解
相关文章:

代码随想录训练营 Day32打卡 动态规划 part01 理论基础 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
代码随想录训练营 Day32打卡 动态规划 part01 一、 理论基础 动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。 例如:有N件物品和一个最多能背重量为W 的背包…...

【智能流体力学】剖析ANSYS Fluent材料属性设定与边界条件
目录 一、材料属性设定**1. 材料属性的概述****功能****2. 材料属性的类型****标准材料库****多相流****燃烧模型****传热模型****辐射模型****3. 属性设置与函数****4. 自定义材料数据库****5. Granta数据库支持**二、边界条件**1. 通用边界条件****Pressure Inlet (压力-入口…...

微信小程序反编译工具
目录 介绍 工程结构还原 微信开发者工具运行 如何查看当前运行版本? 开启小程序F12 重新打包运行 效果示例 安装 用法 参数说明 获取微信小程序AppID 文件夹名即为AppID 下载地址 介绍 纯Golang实现,一个用于自动化反编译微信小程序的工具,小程序安全利器, 自…...

线程基本概念
一、进程的结束 wait(阻塞) 一般不做额外的事情 wait(非阻塞) 逻辑不受影响(必须套在循环中) wait作用:1.获取子进程退出状态 2.回收资源 传参为指针:被调修改主调 获取退出状态值: WIFEXITED 判断是否…...

在SpringBoot中执行后台任务
在 Spring Boot 中执行后台任务通常涉及到使用线程池和定时任务。Spring Boot 提供了多种方式来实现后台任务,包括使用 Scheduled 注解、ThreadPoolTaskExecutor 和 ExecutorService。 下面我将详细介绍如何使用这些方法来实现后台任务。 使用 Scheduled 注解 Sp…...

【网络】UDP回显服务器和客户端的构造,以及连接流程
回显服务器(Echo Server) 最简单的客户端服务器程序,不涉及到业务流程,只是对与 API 的用法做演示 客户端发送什么样的请求,服务器就返回什么样的响应,没有任何业务逻辑,没有进行任何计算或者…...

【智能流体力学】ANSYS Fluent工作流程设置、求解和后处理详解
目录 一、设置阶段1. **模型****功能** :**详细说明及原理** :2. **材料****功能** :**详细说明及原理** :3. **单元区域条件****功能** :**详细说明及原理** :4. **边界条件****功能** :**详细说明及原理** :5. **网格交界面****功能** :**详细说明及原理** :6. **动…...
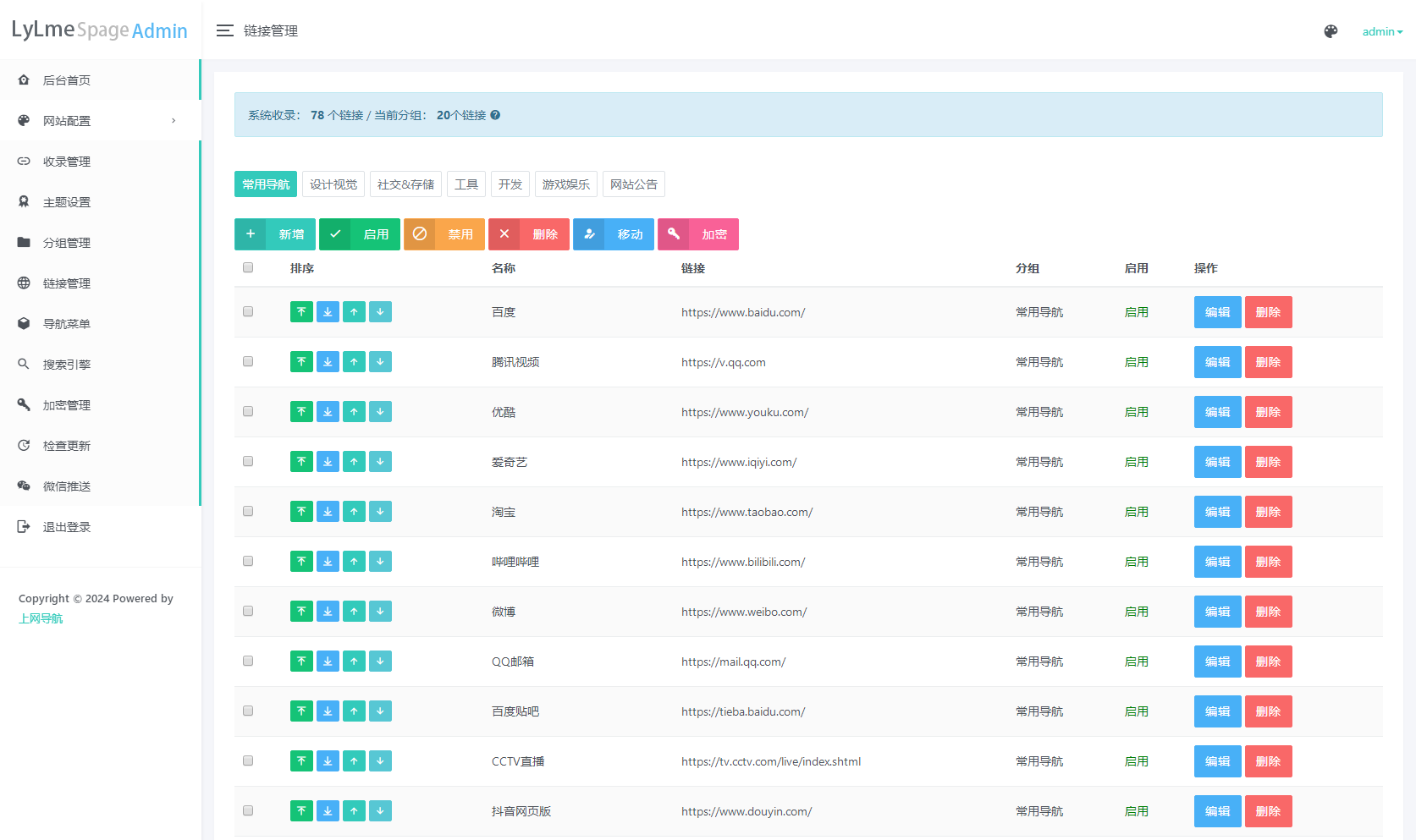
最新UI六零导航系统源码 | 多模版全开源
六零导航页 (LyLme Spage) 致力于简洁高效无广告的上网导航和搜索入口,支持后台添加链接、自定义搜索引擎,沉淀最具价值链接,全站无商业推广,简约而不简单。 使用PHPMySql,增加后台管理 多模板选择,支持在…...

K8S中使用英伟达GPU —— 筑梦之路
前提条件 根据不同的操作系统,安装好显卡驱动,并能正常识别出来显卡,比如如下截图: GPU容器创建流程 containerd --> containerd-shim--> nvidia-container-runtime --> nvidia-container-runtime-hook --> libnvid…...

2024-2025年最值得选的Java计算机毕业设计选题大全:800个热门选题
一、前言 博主介绍: ✌我是阿龙,一名专注于Java技术领域的程序员,全网拥有10W粉丝。作为CSDN特邀作者、博客专家、新星计划导师,我在计算机毕业设计开发方面积累了丰富的经验。同时,我也是掘金、华为云、阿里云、InfoQ…...

libnl教程(2):发送请求
文章目录 前言示例示例代码构造请求创建套接字发送请求 简化示例 前言 前置阅读要求:libnl教程(1):订阅内核的netlink广播通知 本文介绍,libnl如何向内核发送请求。这包含三个部分:构建请求;创建套接字;发送请求。 …...

【软件测试】功能测试理论基础
目录 项目的测试流程🏴 需求评审 评审形式 测试人员在需求评审中职责 测试计划与方案 测试计划 问题 测试方案🏴 测试计划与方案的对比 功能测试设计🏴 测试设计的步骤 项目的测试流程🏴 作用: 有序有效开展…...

玩机进阶教程-----回读 备份 导出分区来制作线刷包 回读分区的写入与否 修改xml脚本
很多工作室需要将修改好的系统导出来制作线刷包。前面分享过很多制作线刷包类的教程。那么一个机型中有很多分区。那些分区回读后要写入。那些分区不需要写入。强写有可能会导致不开机 不进系统的故障。首先要明白。就算机型全分区导出后在写回去 都不一定可以开机进系统。那么…...

MongoDB 插入文档
MongoDB 插入文档 MongoDB 是一个流行的 NoSQL 数据库,它使用文档存储数据。在 MongoDB 中,数据以 BSON(Binary JSON)格式存储,这是一种二进制表示的 JSON 格式。MongoDB 提供了灵活的数据模型,使得插入和查询文档变得非常简单。本文将详细介绍如何在 MongoDB 中插入文档…...

【内网】服务器升级nginx1.17.0
今天用rpm包升级内网nginx版本,上来就给我报错 警告:nginx-1.27.0-2.el7.ngx.x86_64.rpm: 头V4 RSA/SHA256 Signature, 密钥 ID 7bd9bf62: NOKEY 错误:依赖检测失败: libcrypto.so.10()(64bit) 被 nginx-1:1.27.0-2.el7.ngx.x…...

歌曲爬虫下载
本次编写一个程序要爬取歌曲音乐榜https://www.onenzb.com/ 里面歌曲。有帮到铁子的可以收藏和关注起来!!!废话不多说直接上代码。 1 必要的包 import requests from lxml import html,etree from bs4 import BeautifulSoup import re impo…...

transformer-explainer
安装和启动 找到这个项目,然后装好了。 这个项目的目的如名字。 https://github.com/poloclub/transformer-explainerTransformer Explained: Learn How LLM Transformer Models Work with Interactive Visualization - poloclub/transformer-explainerhttps:/…...

C#中的S7协议
S7协议-S7COMM S7COMM 进行写 CTOP->PDU type已知枚举值 0X0E连接请求0x0d连接确认0x08断开请求0x0c断开确认0x05拒绝访问0x01加急数据0x02加急数据确认0x04用户数据0x07TPDU错误0x0f数据传输 S7Header->ROSCTR已知枚举值 0X01JOB REQUEST。主站发送请求0x02Ack。从站…...

2024-08-16升级记录:使用Android RecyclerView控件显示列表型信息
在页面上使用RecyclerView实现一个列表型信息展示: 步骤如下: 一、在页面布局中添加RecyclerView控件 <TextViewandroid:id"id/txt_gnss_info"android:layout_width"match_parent"android:layout_height"wrap_content"…...
 基础实例)
通义千问 ( 一 ) 基础实例
1.相关概念 1.1.模型与平台 1.1.1.通义千问 通义千问 : 是阿里云研发的大语言模型;用于理解和分析用户输入的自然语言,在不同领域和任务为用户提供服务和帮助。 具体应用场景如下: 文字创作:撰写故事、公文、邮件、剧本和诗歌…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
