2022-12-10青少年软件编程(C语言)等级考试试卷(六级)解析
2022-12-10青少年软件编程(C语言)等级考试试卷(六级)解析
T1、区间合并
给定 n 个闭区间 [ai; bi],其中i=1,2,...,n。任意两个相邻或相交的闭区间可以合并为一个闭区间。例如,[1;2] 和 [2;3] 可以合并为 [1;3],[1;3] 和 [2;4] 可以合并为 [1;4],但是[1;2] 和 [3;4] 不可以合并。
我们的任务是判断这些区间是否可以最终合并为一个闭区间,如果可以,将这个闭区间输出,否则输出no。
时间限制:1000
内存限制:65536
输入
第一行为一个整数n,3 ≤ n ≤ 50000。表示输入区间的数量。 之后n行,在第i行上(1 ≤ i ≤ n),为两个整数 ai 和 bi ,整数之间用一个空格分隔,表示区间 [ai; bi](其中 1 ≤ ai ≤ bi ≤ 10000)。
输出
输出一行,如果这些区间最终可以合并为一个闭区间,输出这个闭区间的左右边界,用单个空格隔开;否则输出 no。
样例输入
5
5 6
1 5
10 10
6 9
8 10
样例输出
1 10
//样例代码 结构体排序
#include <bits/stdc++.h>
using namespace std;
struct Nod{int x,y;friend bool operator <(Nod a,Nod b){if(a.x!=b.x)return a.x<b.x;else return a.y<b.y;}
}node[50005];
int main()
{ int n;cin>>n;for(int i=0;i<n;i++)cin>>node[i].x>>node[i].y;sort(node,node+n);int lf=node[0].x;int rt=node[0].y;for(int i=1;i<n;i++){if(lf<=node[i].x&&node[i].x<=rt){rt=max(rt,node[i].y);}else {cout<<"no";return 0;}}cout<<lf<<" "<<rt;return 0;
}T2、电话号码
给你一些电话号码,请判断它们是否是一致的,即是否有某个电话是另一个电话的前缀。比如:
Emergency 911
Alice 97 625 999
Bob 91 12 54 26
在这个例子中,我们不可能拨通Bob的电话,因为Emergency的电话是它的前缀,当拨打Bob的电话时会先接通Emergency,所以这些电话号码不是一致的。
时间限制:1000
内存限制:65536
输入
第一行是一个整数t,1 ≤ t ≤ 40,表示测试数据的数目。 每个测试样例的第一行是一个整数n,1 ≤ n ≤ 10000,其后n行每行是一个不超过10位的电话号码。
输出
对于每个测试数据,如果是一致的输出“YES”,如果不是输出“NO”。
样例输入
2
3
911
97625999
91125426
5
113
12340
123440
12345
98346
样例输出
NO
YES
//示例代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct Trie
{int c[10],s;Trie(){memset(c,0,sizeof(c));s=0;}
}t[N];int tot;
void clear(int x)
{t[x].s=0;for(int i=0;i<=9;i++)if(t[x].c[i])clear(t[x].c[i]),t[x].c[i]=0;
}
char s[15];
bool bt(int x)
{int len=strlen(s+1);bool bk=false;for(int i=1;i<=len;i++){int y=s[i]-'0';if(!t[x].c[y])t[x].c[y]=++tot;else if(i==len)bk=true;x=t[x].c[y];if(t[x].s)bk=true;}t[x].s++;return bk;
}
int main()
{int T;scanf("%d",&T);while(T--){bool bk=false;clear(0);tot=0;int n;scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%s",s+1);if(bk)continue;if(bt(0))bk=true;}if(bk)puts("NO");else puts("YES");}return 0;
}
T3、扑克牌排序
假设这里有36张扑克牌,分别为A1~A9,B1~B9,C1~C9,D1~D9,其中A代表方片,B代表草花,C代表红桃,D代表黑桃,那么,设定如下的排序规则:
1.对于两张卡牌,X1Y1与X2Y2,X1与X2表示A~D,Y1与Y2表示1~9,如果X1与X2不同,那么依照D>C>B>A的方式进行排序
2.假如有X1与X2相同时,那么就比较Y1与Y2的大小。
例如,对于如下的四张牌,有如下的升序排序结果:
D3,C4,A4,C1
升序排序的结果为A4,C1,C4,D3
有人提出了如下的排序策略:
先建立9个队列,用于存放点数的大小,将卡牌依点数存放入各自的队列之中,然后再按队列1到队列9依次出队。
例如,对于上面的结果,依次进队后,结果如下:
队列1:C1;队列3:D3,队列4:C4,A4
将其依次出队后,结果为C1,D3,C4,A4
然后,再建立4个队列,用于存放花色。将卡牌依花色A~D存放入队列1~4中,然后再按队列1到队列4依次出队。
例如,对于上面刚刚出队的序列C1,D3,C4,A4,将其依次进队,结果如下:
队列1:A4;队列3:C1,C4;队列4:D3
将其依次出队后,结果为A4,C1,C4,D3,排序结束。
请根据上面的算法,编写一个用队列对扑克牌排序的程序,要求依照上面的排序规则,根据先花色后点数的方法进行排序。
时间限制:1000
内存限制:65536
输入
输入分为两行,第一行为一个整数n,表示一共有n张牌(1<=n<=100) 第二行用XY的形式表示每一张牌,其中X为A~D,Y为1~9
输出
输出三个部分 第一个部分为第一次进队出队的结果,用Queue1:...表示,共9行,结果用空格分隔,下同 第二部分为第二次进队出队的结果,用QueueA:...表示,共4行 第三部分为一行,即将卡牌排序后的结果(升序排序)
样例输入
8
D8 A6 C3 B8 C5 A1 B5 D3
样例输出
Queue1:A1
Queue2:
Queue3:C3 D3
Queue4:
Queue5:C5 B5
Queue6:A6
Queue7:
Queue8:D8 B8
Queue9:
QueueA:A1 A6
QueueB:B5 B8
QueueC:C3 C5
QueueD:D3 D8
A1 A6 B5 B8 C3 C5 D3 D8
提示
第二次入队出队时,可以复用第一次时9个队列中的4个。所以其实只需要开辟9个队列即可。
//示例代码 队列的基本操作 模拟一下即可
#include <bits/stdc++.h>
using namespace std;
int main()
{ int n;string s;queue<string> qn[9];queue<string> color[4];queue<string> qs;cin>>n;for(int i=1;i<=n;i++){cin>>s;int t=s[1]-'0'-1;qn[t].push(s);}for(int i=0;i<=8;i++){cout<<"Queue"<<i+1<<":";while(!qn[i].empty()){s=qn[i].front();switch (s[0]) {case 'A':color[0].push(s);break;case 'B':color[1].push(s);break;case 'C':color[2].push(s);break;case 'D':color[3].push(s);break;}qn[i].pop();cout<<s<<" ";}cout<<endl; }for(int i=0;i<=3;i++){cout<<"Queue"<<(char)('A'+i)<<":";while(!color[i].empty()){s=color[i].front();color[i].pop();qs.push(s);cout<<s<<" ";}cout<<endl; }while(!qs.empty()){cout<<qs.front()<<" ";qs.pop();}return 0;
}T4、现代艺术
在对二维艺术作品感到厌烦之后,伟大的艺术牛Picowso决定从事创作一项更为小众的艺术形式,一维画。
尽管目前她的画作可以用一个由颜色组成的长度为N(1~100000)的数组表示,但她的创作风格依然保持不变:从一张空白的矩形画布上,不断地画上一些矩形,在一维的情况下,这些矩形就只是一个区间。她用N种颜色,颜色编号为1~N进行创作,每种颜色只使用一次,之后使用的颜色可以完全的覆盖之前在相同位置上的颜色。
令Picowso感到十分沮丧的是,她的竞争对手Moonet似乎弄明白了如何复制她的这些一维画作,Moonet会画一些不相交的间隔,等待这些颜色晾干,然后再画另外的一些间隔,直到画完。Moonet每次每种颜色最多只能画一个间隔,但是他可以一次画不同颜色不相交的多个间隔,只要这些间隔没有重叠部分。之后Moonet再进行下一轮绘制。请计算Moonet为了复制一幅画需要画几个回合。
时间限制:10000
内存限制:65536
输入
第一行是一个整数N,之后N行包含了N个整数,范围0到N表示纸带每个格点的颜色,0表示没有涂色。
输出
输出一行,需要复制这幅画作的最少回合数,如果这幅画不可能是Picowso的画作输出-1(比如说这幅画不可能是通过一次在一条上画一层的方法进行创作的)
样例输入
7
0
1
4
5
1
3
3
样例输出
2
提示
在这个样例中,第一轮涂成0111133,第二轮涂成0145133,所以共需两轮。
// 示例代码 栈的灵活应用
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int end_pos[N], a[N];
int n, result, flag = 1;
char v[N];
stack<int> s;
int main(){scanf("%d", &n);for(int i = 1;i <= n;i += 1){scanf("%d", &a[i]);end_pos[a[i]] = i; //记录每个颜色的终点位置}v[0] = 1;// 初始化 将0视为覆盖整个画布的第一种颜色end_pos[0] = n + 1;s.push(0); for(int i = 1;i <= n && flag;i++){if(s.top() != a[i]){if(v[a[i]]) flag = 0;//颜色被使用过 标记非法s.push(a[i]); //加入新的颜色}v[a[i]] = 1; //标记该颜色被使用过result = max(result, (int)s.size()); if(i == end_pos[a[i]]){s.pop();//该颜色最后一次被使用 弹出改颜色} }if(!flag) cout<<-1;else cout<<result-1;return 0;
}相关文章:
等级考试试卷(六级)解析)
2022-12-10青少年软件编程(C语言)等级考试试卷(六级)解析
2022-12-10青少年软件编程(C语言)等级考试试卷(六级)解析T1、区间合并 给定 n 个闭区间 [ai; bi],其中i1,2,...,n。任意两个相邻或相交的闭区间可以合并为一个闭区间。例如,[1;2] 和 [2;3] 可以合并为 [1;3…...

太酷了,用Python实现一个动态条形图!
大家好,我是小F~说起动态条形图,小F之前推荐过两个Python库,比如「Bar Chart Race」、「Pandas_Alive」,都可以实现。今天就给大家再介绍一个新的Python库「pynimate」,一样可以制作动态条形图,…...
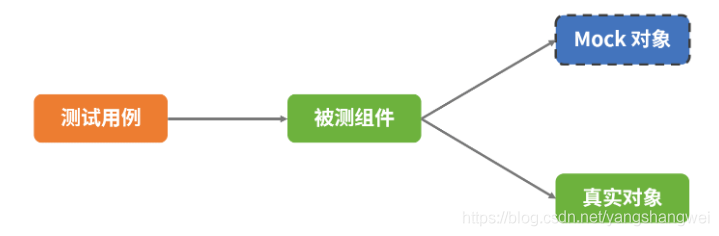
单元测试junit+mock
单元测试 是什么? 单元测试(unit testing),是指对软件中的最小可测试单元进行检查和验证。至于“单元”的大小或范围,并没有一个明确的标准,“单元”可以是一个方法、类、功能模块或者子系统。 单元测试通…...
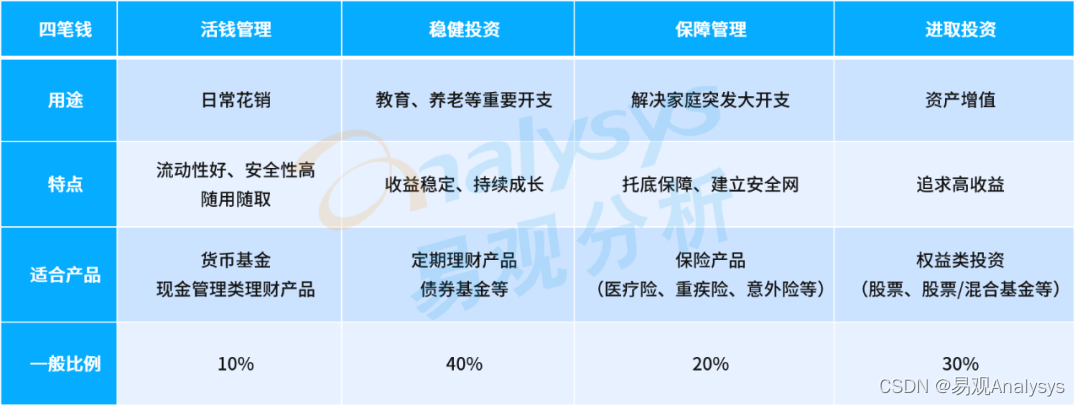
2022Q4手机银行新版本聚焦提升客群专属、财富开放平台、智能化能力,活跃用户规模6.91亿人
易观:2022年第4季度,手机银行APP迭代升级加快,手机银行作为零售银行服务及经营的主阵地,与零售银行业务发展的联系日益紧密。迭代升级一方面可以顺应零售银行发展战略及方向,对手机银行业务布局进行针对性调整优化&…...
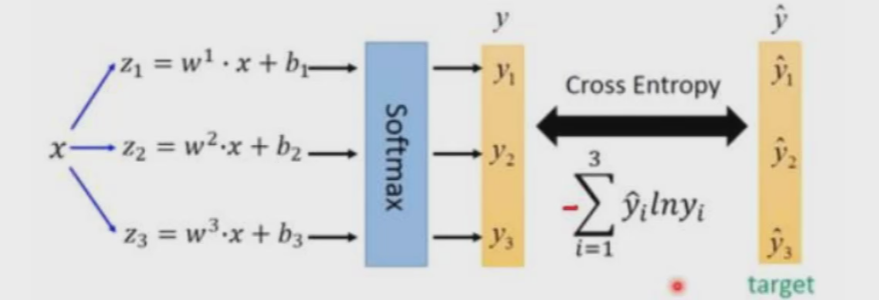
YOLO-V1~V3经典物体检测算法介绍
大名鼎鼎的YOLO物体检测算法如今已经出现了V8版本,我们先来了解一下它前几代版本都做了什么吧。本篇文章介绍v1-v3,后续会继续更新。一、节深度学习经典检测方法概述1.1 检测任务中阶段的意义我们所学的深度学习经典检测方法 ,有些是单阶段的…...
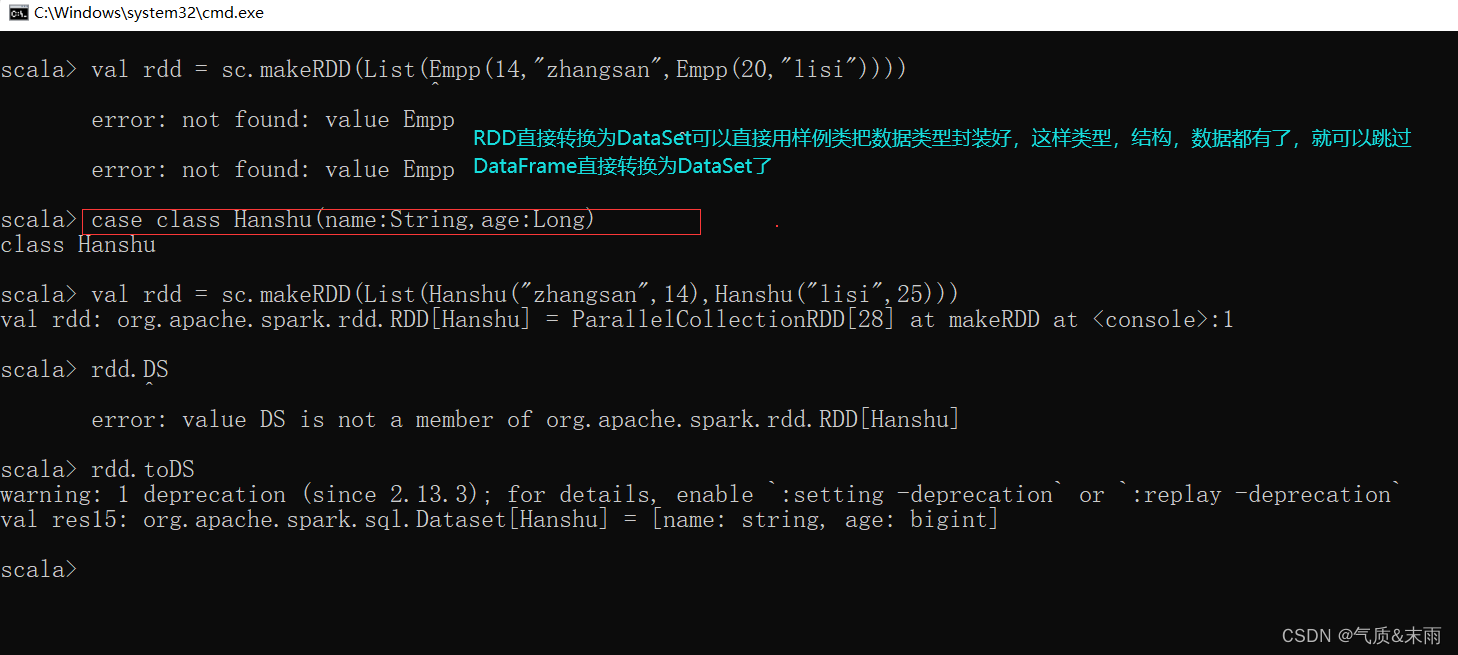
SparkSQL 核心编程
文章目录SparkSQL 核心编程1、新的起点2、SQL 语法1) 读取 json 文件创建 DataFrame2) 对 DataFrame 创建一个临时表3) 通过SQL语句实现查询全表3、DSL 语法1) 创建一个DataFrame2) 查看DataFrame的Schema信息3) 只查看"username"列数据4) 查看"username"列…...
Android核心开发【UI绘制流程解析+原理】
一、UI如何进行具体绘制 UI从数据加载到具体展现的过程: 进程间的启动协作: 二、如何加载到数据 应用从启动到onCreate的过程: Activity生产过程详解: 核心对象 绘制流程源码路径 1、Activity加载ViewRootImpl ActivityThread…...
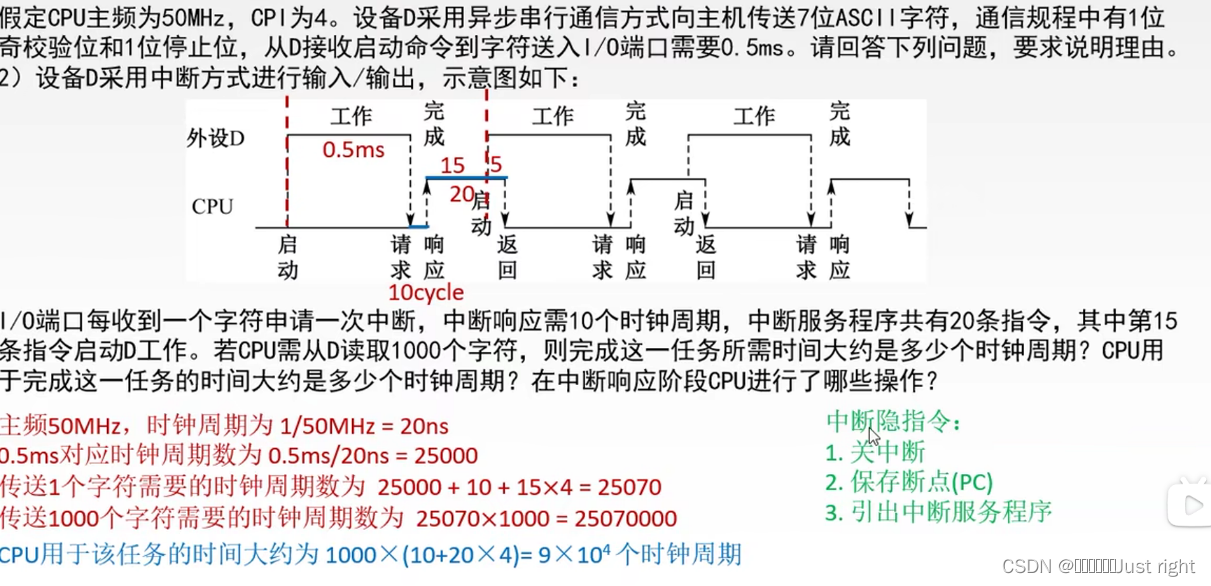
计算机组成原理第七章笔记记录
仅仅作为笔记记录,B站视频链接,若有错误请指出,谢谢 基本概念 演变过程 I/O系统基本组成 I/O软件 包括驱动程序、用户程序、管理程序、升级补丁等 下面的两种方式是用来实现CPU和I/O设备的信息交换的 I/O指令 CPU指令的一部分,由操作码,命令码,设备…...
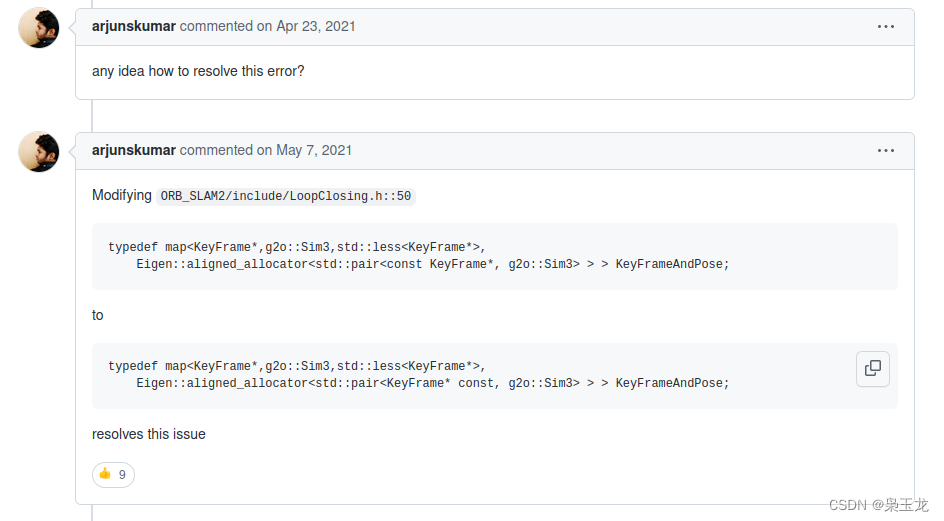
ORB-SLAM2编译、安装等问题汇总大全(Ubuntu20.04、eigen3、pangolin0.5、opencv3.4.10)
ORB-SLAM2编译、安装等问题汇总大全(Ubuntu20.04、eigen3、pangolin0.5、opencv3.4.10) 1:环境说明: 使用的Linux发行版本为Ubuntu 20.04 SLAM2下载地址为:git clone https://github.com/raulmur/ORB_SLAM2.git ORB_SLAM2 2&a…...

QuickBuck:一款专为安全研究人员设计的勒索软件模拟器
关于QuickBuck QuickBuck是一款基于Golang开发的勒索软件模拟工具,在该工具的帮助下,广大研究人员可以通过更简单的方法来判断反病毒保护方案是否能够有效地预防勒索软件的攻击。 功能介绍 该工具能够模拟下列勒索软件典型行为,其中包括&a…...

【八大数据排序法】堆积树排序法的图形理解和案例实现 | C++
第二十一章 堆积树排序法 目录 第二十一章 堆积树排序法 ●前言 ●认识排序 1.简要介绍 2.图形理解 3.算法分析 ●二、案例实现 1.案例一 ● 总结 前言 排序算法是我们在程序设计中经常见到和使用的一种算法,它主要是将一堆不规则的数据按照递增…...

低代码开发平台|生产管理-生产加工搭建指南
1、简介1.1、案例简介本文将介绍,如何搭建生产管理-生产加工。1.2、应用场景在主生产计划列表中下达加工后,在加工单列表可操作领料、质检。2、设置方法2.1、表单搭建1)新建表单【产品结构清单(BOM)】,字段…...
Python类型-语句-函数
文章目录类型动态类型:变量类型会随着程序的运行发生改变注释控制台控制台输入input()运算符算术关系逻辑赋值总结语句判断语句while循环for循环函数链式调用和嵌套调用递归关键字传参在C/java中,整数除以整数结果还是整数,并不会将小数部分舍弃…...

真兰仪表在创业板开启申购:募资约20亿元,IPO市值约为78亿元
2月9日,上海真兰仪表科技股份有限公司(下称“真兰仪表”,SZ:301303)开启申购,将在深圳证券交易所创业板上市。本次上市,真兰仪表的发行价为26.80元/股,市盈率43.06倍。 据贝多财经了解…...
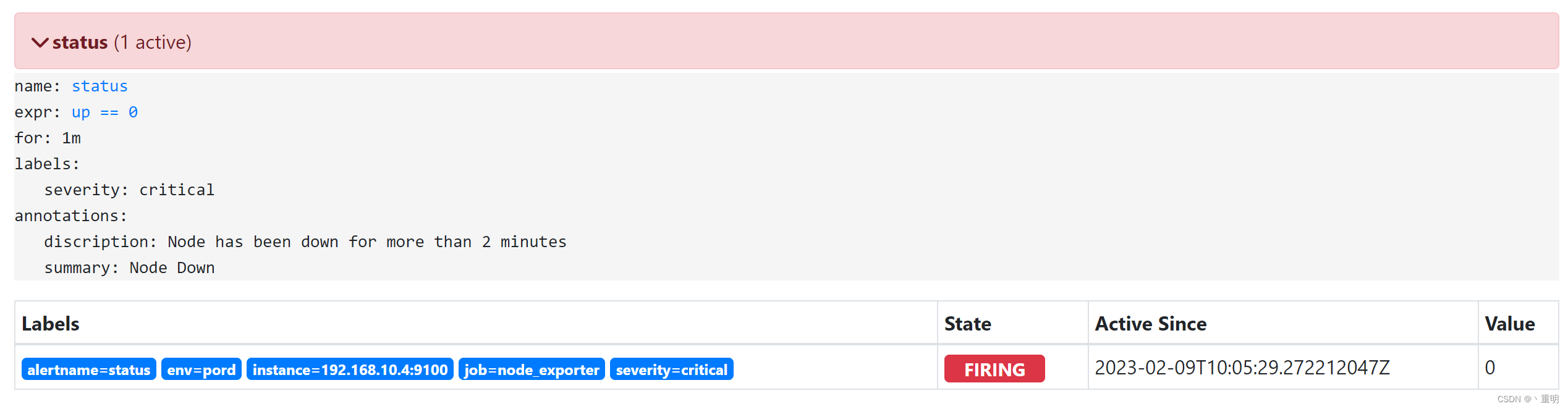
【2023】Prometheus-Prometheus与Alertmanager配置详解
记录一下Prometheus与Alertmanager的配置参数等内容 目录1.Prometheus1.1.prometheus.yml1.2.告警规则定义2.alertmanager2.1.alertmanager.yml2.1.1.global:全局配置2.1.1.1.以email方式作为告警发送方2.1.1.2.以wechat方式作为告警发送方2.1.1.3.以webhook方式作为…...

华为HCIE学习之openstack基础
文章目录一、Openstack各种文件位置二、Openstack命令操作1.使用帮助三、用命令发放云主机1、创建租户2、创建用户并与租户绑定3、注册镜像4、创建规格5、创建公有网络及其子网(做弹性IP用)6、创建私有网络及其子网7、创建路由并设置网关与端口8、创建安…...
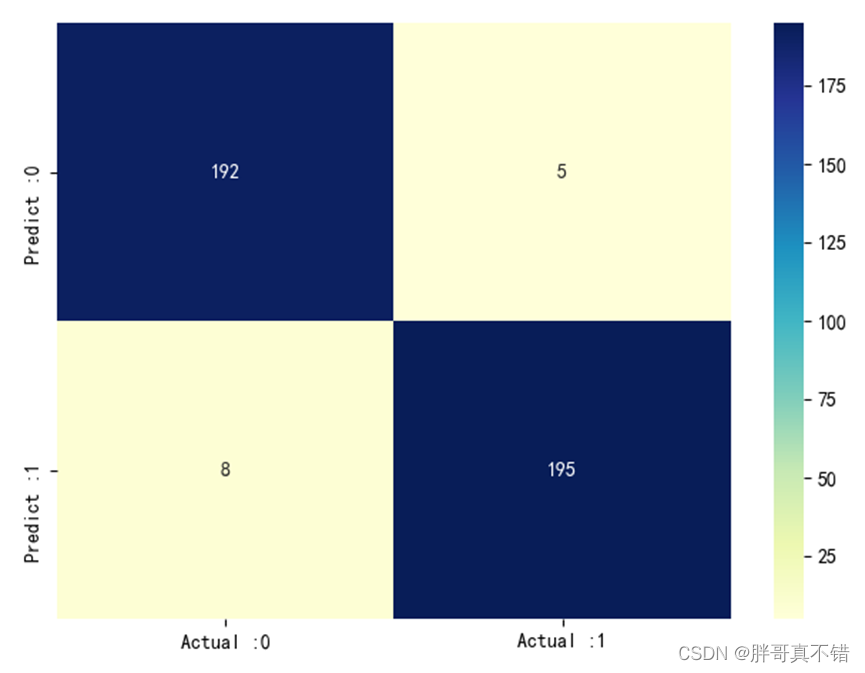
Python实现贝叶斯优化器(Bayes_opt)优化BP神经网络分类模型(BP神经网络分类算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。1.项目背景贝叶斯优化器(BayesianOptimization) 是一种黑盒子优化器,用来寻找最优参数。贝叶斯优化器是基…...
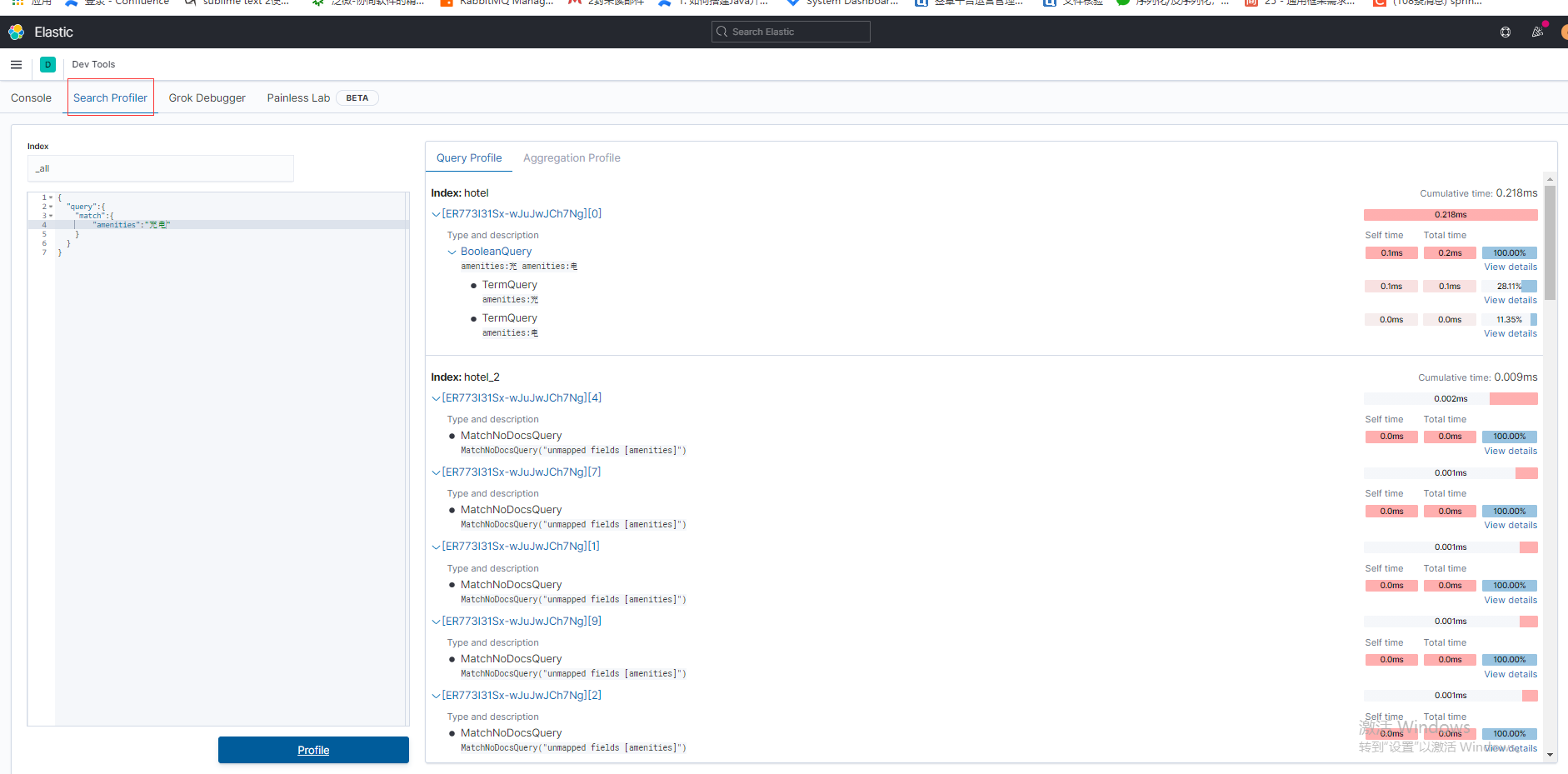
Elasticsearch(九)搜索---搜索辅助功能(下)--搜索性能分析
一、前言 上篇文章我们学习了ES的搜索辅助功能的一部分–分别是指定搜索返回的字段,搜索结果计数,分页,那么本次我们来学习一下ES的性能分析相关功能。 二、ES性能分析 在使用ES的过程中,有的搜索请求的响应比较慢,…...
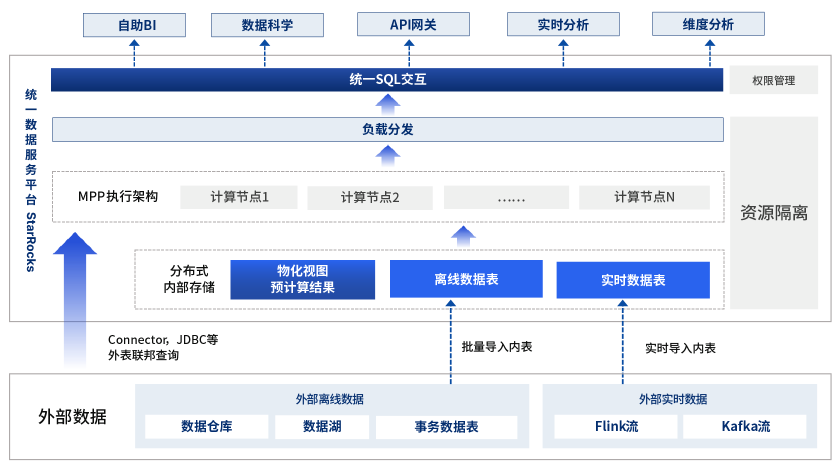
化繁为简|中信建投基于StarRocks构建统一查询服务平台
近年来,在证券服务逐渐互联网化,以及券商牌照红利逐渐消退的行业背景下,中信建投不断加大对数字化的投入,尤其重视数据基础设施的建设,期望在客户服务、经营管理等多方面由经验依赖向数据驱动转变,从而提高…...

2023数字中国创新大赛·数据开发赛道首批赛题启动报名
由数字中国建设峰会组委会主办的2023数字中国创新大赛(DCIC 2023)已正式启幕,本届大赛结合当下数字技术发展的热点和业界关注的焦点,面向产业实际需求设置了九大赛道。其中,数据开发赛道2月8日正式上线首批赛题&#x…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
