微信小程序--27(自定义组件4)
一、父子组件之间通信的3种方式
1、属性绑定
用于父组件向子组件的只当属性设置数据,但只能设置JSON兼容的数据
2、事件绑定
用于子组件向父组件传递数据,可以传递任意数据
3、获取组件实例
父组件还可以通过this.select Component()获取子组件的实例对象,这可直接访问子组件的任意数据和方法
二、属性绑定
属性绑定用于实现父向子传值,而且只能传递普通类型的数据,无法将方法传递给子组件
示例:
1、先创建一个组件test5,在component文件目录下
2、在wxml文件中进行属性绑定
home.wxml文件中,父组件的中count值
<test5 count="{{count}}"></test5>
<view>父组件中,count的值是:{{count}}</view>//test5.js文件中,指定count的类型
properties:{count:Number
}test5.wxml文件中count的值,并实现子组件count值自增<view>子组件中count的值是:{{count}}</view>
<button bindtap="addcount">+1</button>test.js文件中,实现自增
methods:{addcount(){this.setData({count:this.properties.count+1
})
}}会发现count自增并没有同步到父组件当中,这里我们要用到事件绑定事件。
三、事件绑定
用于子组件向父组件传递数据,可以传递任意数据。
使用步骤如下:
- 在父组件的js中,定义一个函数,这个函数即将通过自定义事件的形式,传递给子组件
-
//home.js文件中syncCount(e){console.log(e) }) - 在父组件的wxml中,通过自定义时间的形式,将步骤1定义的函数引用,传递给子组件
-
home.wxml文件中,父组件的中count值 <test5 count="{{count}}" bind:sync="syncCount"></test5> <view>父组件中,count的值是:{{count}}</view> - 在子组件的js文件中,调用this.triggerEvent(‘自定义事件的名称',{/*参数对象*/}),将数据发送到父组件
-
test.js文件中,实现自增,触发自定义事件将数值同步给父组件 methods:{addcount(){this.setData({count:this.properties.count+1 })this.triggerEvent('sync',{value:this.properties.count}) }} - 在父组件的js中,通过e.detail获取到子组件传递过来的数据
-
//home.js文件中syncCount(e){this.setData({ count:e.detail.value })
四、获取组件实例
可在父组件里调用this.selectComponent('id或者class选择器'),获取子组件的实例对象,从而直接访问子组件的任意数据和方法,调用时需要传入一个选择器。
home.wxml文件
<test5 count="{{count}}" bind:sync="syncCount" class="custom" id="cA"> </test5>
<button bindtap="getChild">获取子组件实例</button>//home.js文件中
getChild(){const child = this.selectComponent('custom')
child.setData({count:child.properties.count+1})
child.addCount()
},相关文章:
)
微信小程序--27(自定义组件4)
一、父子组件之间通信的3种方式 1、属性绑定 用于父组件向子组件的只当属性设置数据,但只能设置JSON兼容的数据 2、事件绑定 用于子组件向父组件传递数据,可以传递任意数据 3、获取组件实例 父组件还可以通过this.select Component()获取子组件的实…...

Linux | Linux进程万字全解:内核原理、进程状态转换、优先级调度策略与环境变量
目录 1、从计算机组成原理到冯诺依曼架构 计算机系统的组成 冯诺依曼体系 思考:为什么计算机不能直接设计为 输入设备-CPU运算-输出设备 的结构? 2、操作系统(Operator System) 概念 设计OS的目的 描述和组织被管理对象 3、进程 基本概念 进程id和父进程…...
VBA技术资料MF184:图片导入Word添加说明文字设置格式
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。“VBA语言専攻”提供的教程一共九套,分为初级、中级、高级三大部分,教程是对VBA的系统讲解&#…...

在函数设计中应用单一职责原则:函数分解与职责分离
在函数设计中应用单一职责原则:函数分解与职责分离 引言 单一职责原则(Single Responsibility Principle, SRP)是面向对象设计原则中的核心原则之一,强调一个类或函数应该只有一个责任或理由去改变。在函数设计中,应…...

多线程锁机制面试
目录 乐观锁的底层原理 ReentrantLock的实现原理 读写锁 ReentrantReadWriteLock synchronized 底层原理 Lock和synchronized的区别 乐观锁的底层原理 版本号机制 在数据库表中添加一个版本号字段(如 version),每次更新数据时都会将版本号…...

《SQL 中计算地理坐标两点间距离的魔法》
在当今数字化的世界中,地理数据的处理和分析变得越来越重要。当我们面对一个包含地理坐标数据的表时,经常会遇到需要计算两点之间距离的需求。无论是在物流配送路线规划、地理信息系统应用,还是在基于位置的服务开发中,准确计算两…...

微服务可用性设计
一、隔离 对系统或资源进行分割,实现当系统发生故障时能限定传播范围和影响范围。进一步的,通过隔离能够降低系统之间得耦合度,使得系统更容易维护和扩展。某些业务场景下合理使用隔离技巧也能提高整个业务的性能。我理解隔离本质就是一种解…...

【扒代码】dave readme文档翻译
jerpelhan/DAVE (github.com) 摘要 低样本计数器估算选定类别对象的数量,即使在图像中只有少量或没有标注样本的情况下。目前最先进的技术通过对象位置密度图的总和来估算总数量,但这种方法无法提供单个对象的位置和大小,这对于许多应用来说…...

c语言---文件
这一节我准备分三个部分来带领大家了解文件 ——一、有关文件的基础知识 ————二、文件的简单操作 ————————三、文件结束的判定 ————————————四、文件缓冲区 一、文件的基础知识: 首先在了解文件之前,我们需要了解C/C程序内存…...

Windows系统下Go安装与使用
step1: 下载go语言SDK 下载地址:https://go.dev/dl/ 下载后选择合适位置安装即可,我选择D盘 在安装完成后,可以通过go env 命令检测是否安装成功。在“命令提示符”界面输入“go env”命令,如果显示如下类似结果则说明…...
day24-测试之接口测试基础
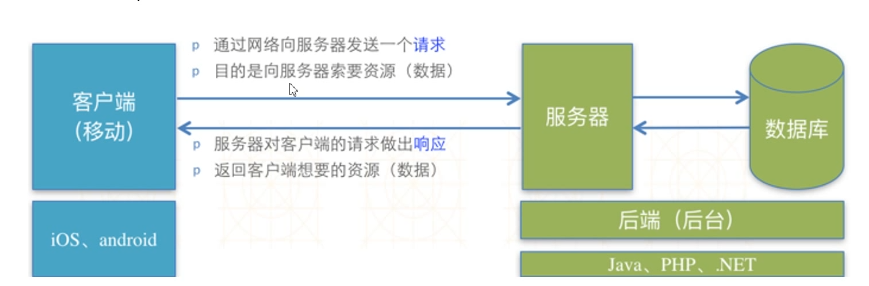
目录 一、接口的定义 二、接口的优点 三、API接口 四、接口测试流程 五、网络基础概念 六、HTTP和RURL 七、get和post请求 八、数据格式 九、状态码 十、restful风格 十一、接口工具 一、接口的定义 程序之间协作所要遵循的一套规范、标准 二、接口的优点 2.1.责任…...

TSN 交换机
TSN(Time-Sensitive Networking)交换机是一种支持时间敏感网络协议的网络交换设备,用于在以太网网络中实现低延迟、高确定性的数据传输。TSN 是一组 IEEE 802 标准的集合,旨在通过标准化的方式,将传统的以太网扩展到需…...

针对thinkphp站点的漏洞挖掘和经验分享
0x1 前言 浅谈 目前在学习和研究thinkphp相关漏洞的打法,然后最近对于thinkphp资产的收集方面有了一个简单的认识,然后写一篇新手看的thinkphp相关的漏洞收集和挖掘的文章来分享下。然后后面是给师傅们分享下后台文件上传,然后直接打一个ge…...

MySQL数据库入门,pycharm连接数据库—详细讲解
一.安装MySQL 1.常用MySQL5.7,首先安装MySQL, (一) (二) (三) (四) (五) 2.配置环境变量 打开MySQL安装路径,在其中找到…...

.bat文件快速运行vue项目
如何使用bat文件快速运行vue项目? 新建个文件,改名为serve.bat。 在文件中写入以下内容: # cd 项目路径 cd D:\projects\xxx npm run serve pausecd 项目所在的路径 npm run dev/serve ,取决于项目的启动方法,打…...

数据结构(邓俊辉)学习笔记】优先级队列 07——堆排序
1.算法 作为完全二叉堆的一个应用,这节来介绍堆排序算法。 是的,谈到优先级队列,我们很自然地就会联想到排序。因为就其功能而言,包括完全二叉堆在内的任何一种优先级队列都天生地具有选取功能,也就是选取其中的最大…...

npm install pnpm -g 报错的解决方法
npm install pnpm -g 报错的解决方法 npm error code ETIMEDOUT npm error errno ETIMEDOUT npm error network request to https://registry.npmjs.org/pnpm failed, reason: npm error network This is a problem related to network connectivity. npm error network In mo…...

集师知识付费小程序开发
智慧生活,从选择一款优质知识付费小程序起航 在这个信息爆炸的时代,知识成为了最宝贵的财富。我们渴望不断学习,提升自我,追求更高品质的生活。而一款优质的知识付费小程序,就如同照亮前行道路的明灯。 它是知识的宝库…...

前端开发提效工具——用户自定义代码片段
做开发总是会有大量的代码要写,但是有时候某些代码是非常基础但是很多,我们就可以把这一部分整合起来,使用一个很简短的关键字来快速唤出。 如何新建这样的代码段? 1.在VSCode当中找到Snippets,然后点击 2.之后会弹出…...
docker容器安全加固参考建议——筑梦之路
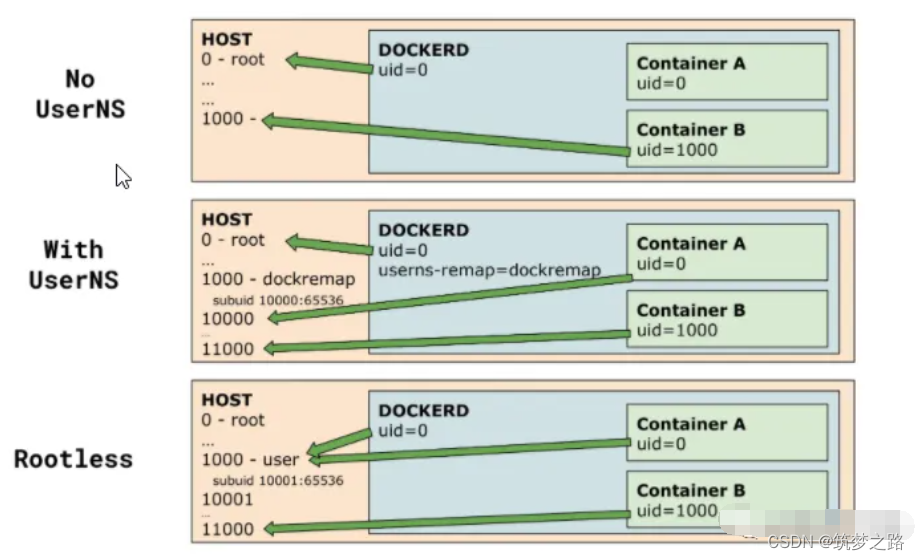
这里主要是rootless的方案。 在以 root 用户身份运行 Docker 会带来一些潜在的危害和安全风险,这些风险包括: 容器逃逸:如果一个容器以 root 权限运行,并且它包含了漏洞或者被攻击者滥用,那么攻击者可能会成功逃出容器…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

若依项目部署--传统架构--未完待续
若依项目介绍 项目源码获取 #Git工具下载 dnf -y install git #若依项目获取 git clone https://gitee.com/y_project/RuoYi-Vue.git项目背景 随着企业信息化需求的增加,传统开发模式存在效率低,重复劳动多等问题。若依项目通过整合主流技术框架&…...

SFTrack:面向警务无人机的自适应多目标跟踪算法——突破小尺度高速运动目标的追踪瓶颈
【导读】 本文针对无人机(UAV)视频中目标尺寸小、运动快导致的多目标跟踪难题,提出一种更简单高效的方法。核心创新在于从低置信度检测启动跟踪(贴合无人机场景特性),并改进传统外观匹配算法以关联此类检测…...

React、Git、计网、发展趋势等内容——前端面试宝典(字节、小红书和美团)
React React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍,详细解释 用户: React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍&#x…...
